Лоренц кеңістігінде Харди-Литтлвуд теңсіздіктерінің Бочкараев типті күшейтілген нұсқалары және Фурье коэффициенттерінің қасиеттері


1. 2 Лоренц кеңістігі үшін Харди-Литтлвуд тәрізді теңсіздіктер
Интегралдық байланыстардың функцияларының қасиеттерінің және Фурье коэффициенттерінің қосындыларының қасиетін көрсететін жақсы таныс Харди-Литтлвуд теңсіздігі, Харди және Литтлвудтың тригонометриялық жүйелер және Лебег кеңістігіндегі функциялар үшін алынған. Пэли шыққан нәтижелерді теңөлшемді шектелген ортонормаланған жүйелер жағдайы үшін жинақтаған. Лоренц кеңістігі үшін айқын нәтижелерді Стейннің еңбектерінен көруге болады.
С. В. Бочкараевтың еңбектерінде Харди-Литтлвудтың классикалық теңсіздіктері Лоренц кеңістігінде басқаша ерекшеленгені көрсетіледі. Ол келесі тұжырымдарды дәлелдеді.
(Бочкараев С. В. )
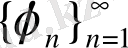 функциясы
функциясы
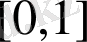 де ортонормаланған комплекстелген функциялар жүйесі болсын.
де ортонормаланған комплекстелген функциялар жүйесі болсын.

және
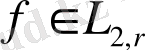
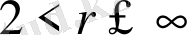 функциясы берілген болсын, онда келесі теңсіздік айқын болады
функциясы берілген болсын, онда келесі теңсіздік айқын болады
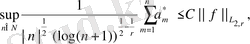
мұндағы
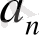 -
-
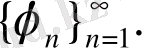 жүйесіндегі Фурье коэффициенттері.
жүйесіндегі Фурье коэффициенттері.
Бочкараев теоремасында теңсіздік
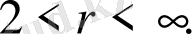 жағдайында алынды.
жағдайында алынды.
 жағдайында теңсіздік қандай түрде болатыны туралы сұрақ пайда болады.
жағдайында теңсіздік қандай түрде болатыны туралы сұрақ пайда болады.
Келесі бөлімшелерде интегралдық байланыстардың функцияларының қасиеттері мен Фурье коэффициенттерінің қосындыларының қасиеттерінің арасындағы байланыстарын көрсететін Харди-Литтлвуд теңсіздіктерінің Лоренц
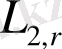
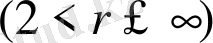 кеңістігі үшін жаңа түрі бар екенін Бочкараев теоремасының жаңа дәлелдеуінде көрсетіледі. Бочкараев теоремасынын дәлелдеу әдісі тригонометриялық қатарлардың спецификасына негізделіп жасалды. Мұнда сызықтық операторлардың экстрополяциясы базалық негізді алып тұрды. Бұл тәсіл Харди-Литтлвуд теңсіздігінің
кеңістігі үшін жаңа түрі бар екенін Бочкараев теоремасының жаңа дәлелдеуінде көрсетіледі. Бочкараев теоремасынын дәлелдеу әдісі тригонометриялық қатарлардың спецификасына негізделіп жасалды. Мұнда сызықтық операторлардың экстрополяциясы базалық негізді алып тұрды. Бұл тәсіл Харди-Литтлвуд теңсіздігінің
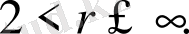 жағдайындағы жаңа дәлелдеу алуға көмектесті. Біз тағы да
жағдайындағы жаңа дәлелдеу алуға көмектесті. Біз тағы да
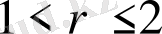 жағдайында Лоренц кеңістігіндегі кейбір ортонормаланған жүйелер үшін жаңа теңсіздік бар екенін дәлелдейміз.
жағдайында Лоренц кеңістігіндегі кейбір ортонормаланған жүйелер үшін жаңа теңсіздік бар екенін дәлелдейміз.
2. Регуляр жүйедегі функция үшін Фурье коэффициенттері
“ Математические заметки ” журналында 2013 жылы шыққан
Мусабаев Г. К. және Тлеуханова Н. Т. мақалаларында Бочкараев теоремасының тригонометриялық жүйе бойынша күшейтілуі алынды.
Лемма 2. 1. 1.
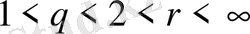 үшін
үшін
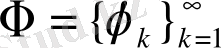 - регулярлы жүйе болсын және
- регулярлы жүйе болсын және
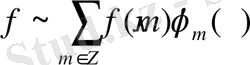 , онда кез келген
, онда кез келген
 дан алынған
дан алынған
 ақырлы ішжиыны үшін келесі теңсіздік дұрыс
ақырлы ішжиыны үшін келесі теңсіздік дұрыс
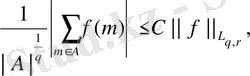
мұндағы
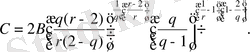
және
 -
-
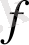 функциясының Фурье коэффициенттері.
функциясының Фурье коэффициенттері.
Лемма 2. 1. 2.
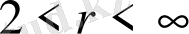 үшін
үшін
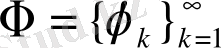 - регулярлы жүйе болсын және
- регулярлы жүйе болсын және
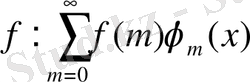 ,
,
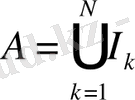 ,
,
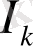 -
-
 -
тен алынған кесінділер болсын. Онда
-
тен алынған кесінділер болсын. Онда
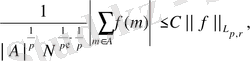
болады және мұндағы
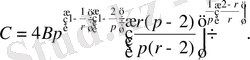
болады.
Лемма 2. 1. 3.
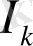 кесінділер үшін
кесінділер үшін
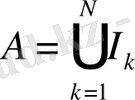 ,
,
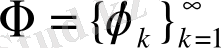 - регулярлы жүйе болсын және
- регулярлы жүйе болсын және
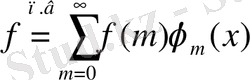 , онда кез келген
, онда кез келген
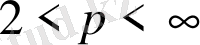 және
және
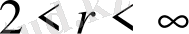 үшін келесі теңсіздік айқын
үшін келесі теңсіздік айқын
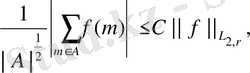
және мұндағы
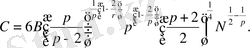
болады.
Теорема А.
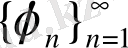 -
-
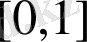 комплексмәнді функциялар жүйесінде ортонормаланған болсын,
комплексмәнді функциялар жүйесінде ортонормаланған болсын,
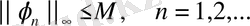
Онда кез келген
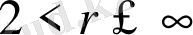 және
және
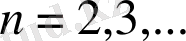 үшін келесі теңсіздік айқын
үшін келесі теңсіздік айқын
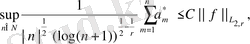 (43)
(43)
мұндағы
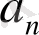 -
-
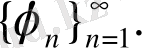 жүйесіндегі Фурье коэффициенттері.
жүйесіндегі Фурье коэффициенттері.
 жиыны барлық
жиыны барлық
 тан алынған арифметикалық прогрессиялар жиыны болсын.
тан алынған арифметикалық прогрессиялар жиыны болсын.
 тан алынған
тан алынған
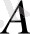 ақырлы жиыны үшін
ақырлы жиыны үшін
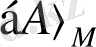 санын келесі түрде анықтайық
санын келесі түрде анықтайық
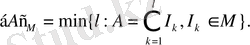
Мұнда дизъюнкциялық бірігу - бұл бірігу қиылыспайтын жиындардың бірігуі, сол сияқты
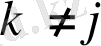 үшін
үшін
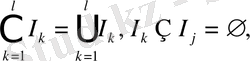
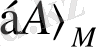 саны- А жиынының құрылымдық қасиеттерін көрсетеді, ал оның ерекшелігі
саны- А жиынының құрылымдық қасиеттерін көрсетеді, ал оның ерекшелігі
 жиынының бірігуі түрінде болады.
жиынының бірігуі түрінде болады.
Бұл бөлімшенің негізгі нәтижесі келесі тұжырым болады.
Теорема 2. 2. 1.
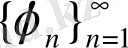 - регулярлы жүйе және
- регулярлы жүйе және
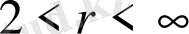 ,
,
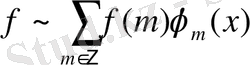 болсын. Онда кез келген
болсын. Онда кез келген
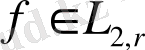 функциясы үшін келесі теңсіздік айқын
функциясы үшін келесі теңсіздік айқын
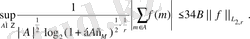 (44)
(44)
Ескерту 2. 2. 1. Дәлелденген теорема тригонометриялық жүйеде ғана Бочкараев теоремасының нәтижесін күшейтеді.
Ескерту 2. 2. 2. (43) - ші теңсіздік келесі теңсіздікпен эквивалентті екенін байқаймыз
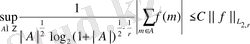
сондықтан (44) -ші теңсіздіктен (43) -ші теңсіздік шығатынын байқаймыз. Кері тұжырым қате. Егер
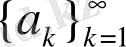 -монотонды тізбек болса, онда
-монотонды тізбек болса, онда
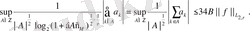
болады.
Мысал 2. 2. 1.
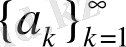 тізбегін келесідей алайық:
тізбегін келесідей алайық:
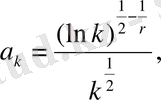
онда
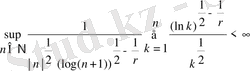
болады, бірақ
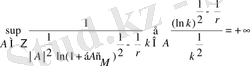
болатыны айқын көрінеді.
2. 3.
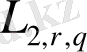 көппараметрлі Лоренц кеңістігіндегі функция үшін Фурье коэффициенттері
көппараметрлі Лоренц кеңістігіндегі функция үшін Фурье коэффициенттері
Анықтама 2. 3. 1.
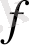 -өлшеммді функция болсын.
-өлшеммді функция болсын.
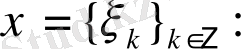 ны анықтайық
ны анықтайық
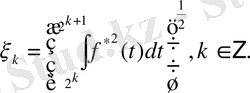
Егер
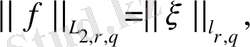 болса, онда
болса, онда
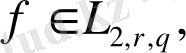 деп айта аламыз,
деп айта аламыз,
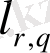 -
дискретті Лоренц кеңістігі.
-
дискретті Лоренц кеңістігі.
Теорема 2. 3. 1.
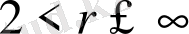 және
және
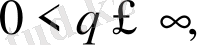 үшін
үшін
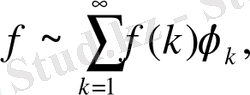 болсын,
болсын,
 ,
,
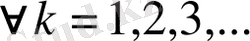 үшін
үшін
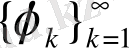 -
ортонормаланған жүйесі болсын. Онда кез келген
-
ортонормаланған жүйесі болсын. Онда кез келген
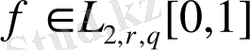 үшін келесі теңсіздік орындалады;
үшін келесі теңсіздік орындалады;
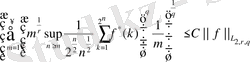 (45)
(45)
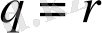 үшін
үшін
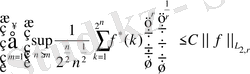 (46)
(46)
немесе
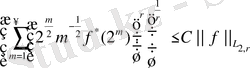 (47)
(47)
Дәлелдеуі:
 жартылыай аддитивті операторын келесідей анықтап алайық:
жартылыай аддитивті операторын келесідей анықтап алайық:
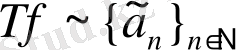 , мұндағы
, мұндағы
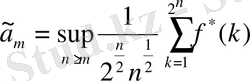 .
.
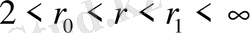 болсын және
болсын және
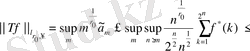
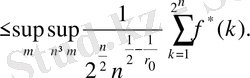
1. 2. 2. теоремасын (Бочараев теоремасы) қолдану арқылы біз
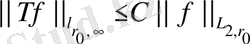
теңсіздігін аламыз. Сонымен
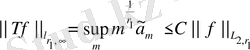
екендігі айқын.
Интерполяциондық теореманы қолдану арқылы біз
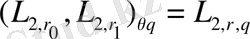 , мұндағы
, мұндағы
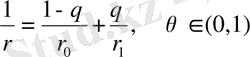 үшін келесі теңсіздік айқын
үшін келесі теңсіздік айқын
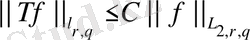
немесе келесі теңсіздік орындалады:
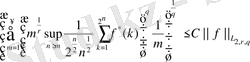
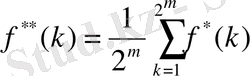 екендігін ескере отырып және орын ауыстырулардың кемімелігінен (47) -ші теңсіәздікті аламыз.
екендігін ескере отырып және орын ауыстырулардың кемімелігінен (47) -ші теңсіәздікті аламыз.
Ескерту 2. 3. 1.
 болған кезде (45) -ші теңсіздік (16) -шы теңсіздікке қарағанда күшті екенін көруге болады.
болған кезде (45) -ші теңсіздік (16) -шы теңсіздікке қарағанда күшті екенін көруге болады.
Дәлелдеуі:
 келесі шартты қанағаттандыратын болсын,
келесі шартты қанағаттандыратын болсын,
 .
.
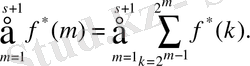 кезде
кезде
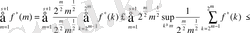
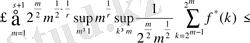
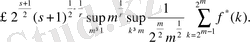
Онда
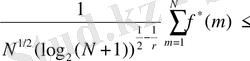
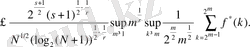
болады. 2. 3. 1. теоремасынан және көппараметрлі Лоренц кеңістігінен келесі теңсіздікті аламыз
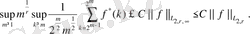 (48)
(48)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz