Факультативтік сабақта шектер теориясын оқытудың әдістемесі


Курстық жұмыс
Қазақстан Республикасы білім және ғылым министрлігі
Академик Е. А. Букетов атындағы Қарағанды университеті
Математика және ақпараттық технологиялар факультеті
Математика және информатиканы оқыту әдістемесі кафедрасы
Курстық жұмыс
Пәні:Сыныптан тыс жұмыс (факультативті сабақ)
Тақырыбы: Факультативтік сабақта шектер теориясын оқыту
Орындаған: МиИ-421 топ студенті
Сайфулла Ш. У
Тексерген: Ахманова. Д. М
Қарағанды-2021
МАЗМҰНЫ
КІРІСПЕ . . . 6
1 ТІЗБЕКТІҢ ШЕГІН ФАКУЛЬТАТИВТІК САБАҚТА ТҮСІНДІРУ . . . 7
1. 1 Сандық тізбек және оның шегі, берілу тәсілдері . . . 7
1. 2 Теңсіздіктерде шекке көшу . . . 9
2 ФУНКЦИЯ ШЕГІ ТЕОРЕМАЛАРЫН СЫНЫПТАН ТЫС ТҮСІНДІРУ . . . 11
- Функция шегінің екі анықтамасы және олардың пара - парлығы. . … . . . 11
- Бір жақты шектер . . . . . . … . . . 12
2. 3 Функцияның шексіздіктегі шегі . . . . . . … . . . … . . . 13
ҚОРЫТЫНДЫ . . . 21
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 22
ҚОСЫМША . . . 23
КІРІСПЕ
Мен өзімнің курстық жұмысымда Шектер теориясы туралы қарастырамыз яғни:
Егер кез - келген оң
 санына сәйкес натурал
санына сәйкес натурал
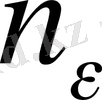 саны табылып, барлық
саны табылып, барлық
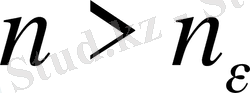 нөмірлері үшін
нөмірлері үшін
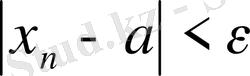 теңсіздігі орындалса, онда
a
саны
теңсіздігі орындалса, онда
a
саны
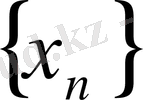 тізбегінің шегі деп аталады және былай жазылады:
тізбегінің шегі деп аталады және былай жазылады:
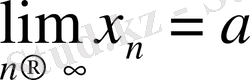
Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
1) Аналитикалық тәсіл. Бұл тәсілді қолданғанда n нөмері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.
2) Рекуренттік тәсіл. Бүл тәсілді қолданғанда тізбектің біріншісі беріледі және осы тізбектің белгілі бір немесе бірнеше алғашқы мүшелері бойынша кез - келген мүшесін табу үшін формула беріледі.
Мысал. а) кез - келген
n
≥ 2 үшін
a = an-1+d;
б) кез - келген
n
≥ 2 үшін
bn
=
bn-1
∙
q
; а) және б) формулалары сәйкес
 және
және
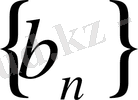 тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
3) Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз болу
мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.
а) 2, 3, 5, 7, 11, . . . ; б) 2; 2, 2; 2, 23; 2, 236; 2, 2361; . . . Бұл тізбектерді былайша баяндайды: бірінші тізбек жай сандар тізбегі, ал екіншісі -
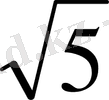 саны үшін кемімен алынған ондық жуықтаулар тізбегі.
саны үшін кемімен алынған ондық жуықтаулар тізбегі.
Функцияның нүктедегі шегі.
Функциясы нүктесінің қандай да бір маңайында ( нүктесінің өзі кірмеуі мүмкін) анықталсын.
Функция нүктедегі шегінің екі өзара эквивалентті анықтамасын тұжырымдайық.
Анықтама 1. («тізбектер» тілінде немесе Гейне бойынша) . Егер -ге жинақталатын, аргументінің мүмкін мәндерінің кез-келген тізбегі А санына жинақталса, А саны функциясының шегі деп аталады. Бұл жағдайда немесе болғанда деп жазады. функциясы шегінің геометриялық мағынасы: нүктесіне жеткілікті жақын барлық нүктесі үшін функцияның сәйкес мәндері санынан аз ғана айырмашылығы болады.
функция шегінің анықтамасы бойынша нүктесі -ге кез-келген жағдайда ұмтылады: ден кіші болса да, ден үлкен болса да немесе нүктесінің аймағында ауытқыса да.
Кейде аргументінің -ге жақындауының тәсілі функция шегінің мәніне айтарлықтай әсер ететін жағдайлар болады. Сондықтан, бір жақты шектер ұғымы енгізіледі.
Егер кез-келген үшін саны табылып, болғанда теңсіздігін орындалса, саны функциясының сол жақ шегі деп аталады. Сол жақ шекті деп немесе қысқаша, деп жазады. Осылайша, функцияның оң жақты шегі анықталып, қысқаша төмендегідей жазылады:
Оң жақты шекті қысқаша деп белгілейді. Функцияның оң жақты және сол жақты шектері бір жақты шектер деп аталады. Егер бар болса, онда екі бір жақты шектер бар болады және . Кері тұжырым да орынды: егер екі бір жақты шектер бар болса және олар тең болса, онда және шегі бар болады. Егер болса, онда шегі жоқ.
1 Тізбектің шегін факультативтік сабақта түсіндіру
- Сандық тізбек және оның шегі, берілу тәсілдері.
Сандық тізбек деп N натурал сандар жиынында анықталған сандық функцияны атайды. Бұл функцияны f әріпімен белгілейік. Сонда анықтама бойынша 1 санына f (1) мәні, 2 санына f (2) мәні т. с. с. сәйкес келеді. Жалпы алғанда ондай сәйкестікті былай белгілейді:
n
 f (n) .
f (n) .
Бұл шамаларды сәйкес түрде
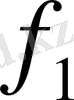 = f
(1),
= f
(1),
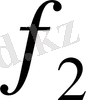 = f
(2), …,
= f
(2), …,
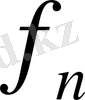 = f
(n), … арқылы белгілеп, оларды тізбектің бірінші, екінші, және т. с. с.
n
-ші мүшелері деп атайды.
n
-ші мүшені тіэбектің жалпы мүшесі дейді. Жалпы мүшесі
= f
(n), … арқылы белгілеп, оларды тізбектің бірінші, екінші, және т. с. с.
n
-ші мүшелері деп атайды.
n
-ші мүшені тіэбектің жалпы мүшесі дейді. Жалпы мүшесі
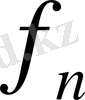 болатын тізбекті
болатын тізбекті
 немесе
немесе
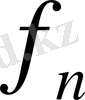 арқылы белгілейді. Осылайша белгілеуде
n
номері
N
натурал сандар жиынының барлық мәндерін қабылдайды деп түсініледі.
арқылы белгілейді. Осылайша белгілеуде
n
номері
N
натурал сандар жиынының барлық мәндерін қабылдайды деп түсініледі.
Тізбекті жазып берудің жиі қолданылатын тәсілдері мыналар:
1) Аналитикалық тәсіл. Бұл тәсілді қолданғанда n нөмері бойынша тізбектің сәйкес мүшесін табу үшін формула жазылып көрсетіледі.
2) Рекуренттік тәсіл. Бүл тәсілді қолданғанда тізбектің біріншісі беріледі және осы тізбектің белгілі бір немесе бірнеше алғашқы мүшелері бойынша кез - келген мүшесін табу үшін формула беріледі.
Мысал. а) кез - келген
n
≥ 2 үшін
a = an-1+d;
б) кез - келген
n
≥ 2 үшін
bn
=
bn-1
∙
q
; а) және б) формулалары сәйкес
 және
және
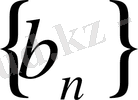 тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
тізбектерінің берілген алдыңғы мүшесі бойынша оның кез - келген мүшесін табуға мүмкіндік береді. Тізбектің рекуренттік тәсілмен берілуі шапшаң есептейтін элетрондық есептеуіш машиналармен жұмыс істегенде аса қолайлы келеді.
3) Баяндап беру тәсілі. Бұл тәсілді қолданғанда тізбек элементтері баяндап айтылатын болады. Бұл жағдайда тізбектің жалпы мүшесі үшін формула да, немесе оның мүшелері үшін рекуренттік қатыс та белгісіз бол
мүмкін. Осы айтылғанды мысалмен түсіндіру үшін мына тізбектерді қарастырайық.
а) 2, 3, 5, 7, 11, . . . ; б) 2; 2, 2; 2, 23; 2, 236; 2, 2361; . . . Бұл тізбектерді былайша баяндайды: бірінші тізбек жай сандар тізбегі, ал екіншісі -
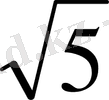 саны үшін кемімен алынған ондық жуықтаулар тізбегі.
саны үшін кемімен алынған ондық жуықтаулар тізбегі.
Тізбектердің қарапайым сипаттамалары.
а) Шенделген және шенделмеген тізбектер. Егер с > 0 саны табылып,
барлық
 үшін
үшін
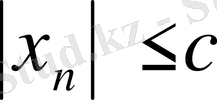 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
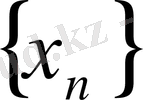 тізбегі шенделген
тізбегі шенделген
тізбек деп аталады. (символдар арқылы :
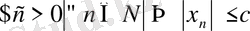 ) . Жоғарыдан
) . Жоғарыдан
және төменнен шенелген тізбектердің анықтамалары осыған ұқсас түрде
тұжырымдалады.
Мысал үшін тізбектің жоғарыдан шенделгендігін символдармен жазылуын келтірейік. Егер
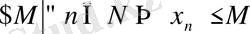 орындалса, онда
орындалса, онда
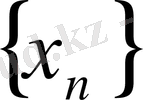 тізбегі жоғарыдан шенделген деп аталады. Сонда М саны тізбектің жоғарғы шені деп аталады. Енді тізбектің шенделгендігін терістеу арқылы оның шенделмегендігінің анықтамасын (символдар көмегімен) берейік. Егер
тізбегі жоғарыдан шенделген деп аталады. Сонда М саны тізбектің жоғарғы шені деп аталады. Енді тізбектің шенделгендігін терістеу арқылы оның шенделмегендігінің анықтамасын (символдар көмегімен) берейік. Егер
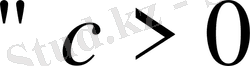 үшін
үшін
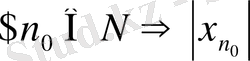 >c орындалса, онда
>c орындалса, онда
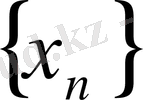 тізбегі шенделмеген деп аталады.
тізбегі шенделмеген деп аталады.
б) Тізбек үшін жұп болу, не тақ болу деген түсініктердің мағынасы болмайды, өйткені N жиыны симмметриялы емес ( N жиынына n саны енгенімен - n саны енбей отыр) .
в) Тізбек үшін периодты, не периодсыз болу деген түсініктердің де мағынасы жоқ, өйткені N жиыны периодты емес.
г)
Бірсарынды тізбектер. Барлық
n
 N
үшін
N
үшін
 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
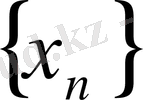 тізбегі өспелі тізбек деп аталады. Егер барлық
n
тізбегі өспелі тізбек деп аталады. Егер барлық
n
 N
үшін
N
үшін
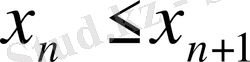 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
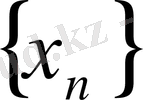 тізбегі кемімейтін аталады. Өспелі, кемімейтін, кемімелі және өспейтін тізбектерді жалпы бірсарынды тізбектер деп атайды.
тізбегі кемімейтін аталады. Өспелі, кемімейтін, кемімелі және өспейтін тізбектерді жалпы бірсарынды тізбектер деп атайды.
Тізбек шегін анықтау
1- анықтама. Егер кез - келген оң
 санына сәйкес натурал
санына сәйкес натурал
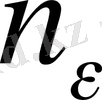 саны табылып, барлық
саны табылып, барлық
 нөмірлері үшін
нөмірлері үшін
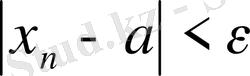 теңсіздігі орындалса, онда
a
саны
теңсіздігі орындалса, онда
a
саны
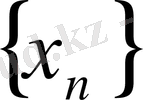 тізбегінің шегі деп аталады және былай жазылады:
тізбегінің шегі деп аталады және былай жазылады:
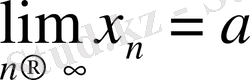 немесе
немесе
 жағдайда
жағдайда
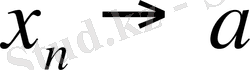 (символдар арқылы
(символдар арқылы
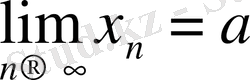
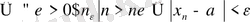 ) . Шегі бар тізбек жинақталатын тізбек деп, ал шегі болмайтын жинақталмайтын тізбек деп аталады. Модуль қасиетінің негізінде
) . Шегі бар тізбек жинақталатын тізбек деп, ал шегі болмайтын жинақталмайтын тізбек деп аталады. Модуль қасиетінің негізінде
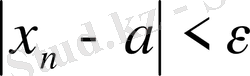 теңсіздігі
теңсіздігі
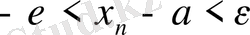 немесе
немесе
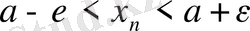 теңсіздігімен пара - пар, олай болса, барлық
теңсіздігімен пара - пар, олай болса, барлық
 үшін
үшін
 , яғни
a
нүктесінің
, яғни
a
нүктесінің
 - маңайы тізбектің
- маңайы тізбектің
 нөмірлі барлық мүшелерін қамтиды.
нөмірлі барлық мүшелерін қамтиды.
Бұдан тізбек шегінің тағы бір анықтамасына келеміз.
2- анықтама. Егер
a
нүктесінің кез - келген
 маңайы
маңайы
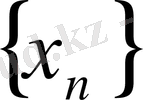 тізбегінің саны арқылы
тізбегінің саны арқылы
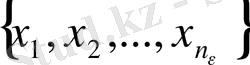 мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы
a
санын
мүшелерінен өзге барлық мүшелерін қамтитын болса, онда осы
a
санын
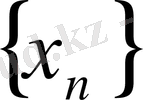 тізбегінің шегі деп атайды.
тізбегінің шегі деп атайды.
1. 2 Шегі бар тізбектердің қасиеттері
1- теорема. Егер
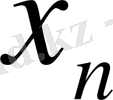 тізбегінің шегі бар болса, онда ол шек жалғыз.
тізбегінің шегі бар болса, онда ол шек жалғыз.
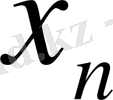 тізбегінің шегі
a
және
b
бар деп жориық. Олардың
тізбегінің шегі
a
және
b
бар деп жориық. Олардың
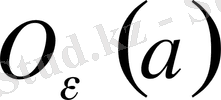 ,
,
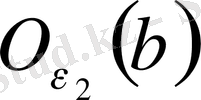 маңайларын
маңайларын
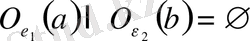 ( яғни қиылыспайтындай) етіп алайық.
( яғни қиылыспайтындай) етіп алайық.
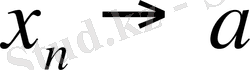 ұмтылғанда
ұмтылғанда
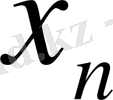 тізбегінің
тізбегінің
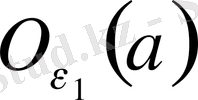 маңайының сыртында жатқан мүшелері арқылы жиын, олай болса
маңайының сыртында жатқан мүшелері арқылы жиын, олай болса
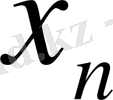 тізбегінің
тізбегінің
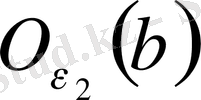 маңайында жатқан мүшелері ақырсыз жиын бола алмайды, сондықтан, анықтама бойынша « b» саны
маңайында жатқан мүшелері ақырсыз жиын бола алмайды, сондықтан, анықтама бойынша « b» саны
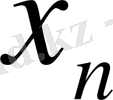 тізбегінің шегі бола алмайды.
тізбегінің шегі бола алмайды.
2- теорема. Егер
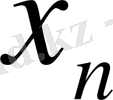 тізбегі жинақты болса, онда ол тізбек - шенелген.
тізбегі жинақты болса, онда ол тізбек - шенелген.
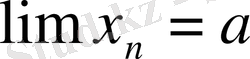 деп алайық.
деп алайық.
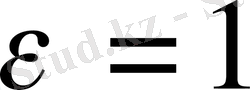 саны берілсін.
саны берілсін.
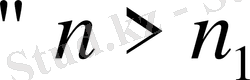 нөмерлері бар
нөмерлері бар
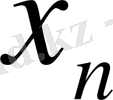 мүшелері үшін
мүшелері үшін
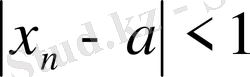 орындалатындай етіп
орындалатындай етіп
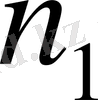 оң бүтін санын табамыз. Онда (
оң бүтін санын табамыз. Онда (
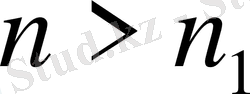 )
)
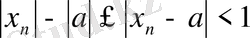 , бұдан
, бұдан
 ,
,
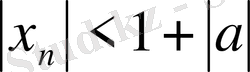 аламыз. Енді
аламыз. Енді
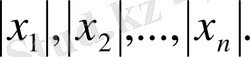 ,
,
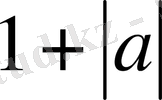 сандарының ең үлкенін
М
деп алсақ, онда
сандарының ең үлкенін
М
деп алсақ, онда

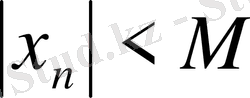 аламыз.
аламыз.
Ескерту. Тізбек жинақты болу үшін тізбектің шенелген болуы қажетті, бірақ бұл - жеткіліксіз шарт.
3 - теорема
.
Егер
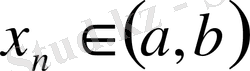 болса, онда
болса, онда
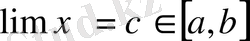
4- теорема. Егер
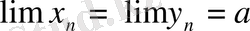 және
және
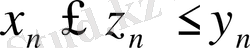 ,
n=
1, 2 . . . болса онда
,
n=
1, 2 . . . болса онда
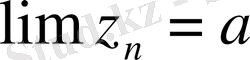
 саны берілсін. Онда
саны берілсін. Онда
 нөмірлері үшін
нөмірлері үшін
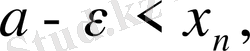
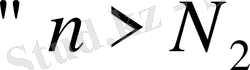 нөмірлері үшін
нөмірлері үшін
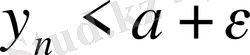
Орындалатындай
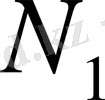 және
және
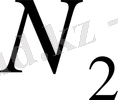 сандары табылады.
сандары табылады.
Ал
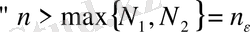 нөмірлері үшін
нөмірлері үшін
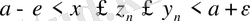
Яғни
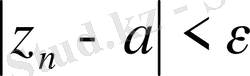 (
(
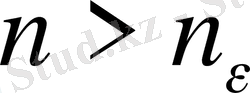 ) орындалады.
) орындалады.
5- теорема
.
Егер
 , онда
, онда
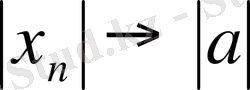 .
.
Кeлесі екі тұжырым, пара-пар: (
 )
)
 (
(
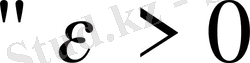 Оң сан берілсе
Оң сан берілсе
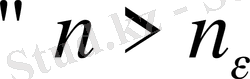 нөмірлері үшін
нөмірлері үшін
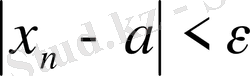 теңсіздігі орындалатындай
теңсіздігі орындалатындай
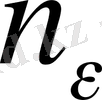 саны табылады) .
саны табылады) .
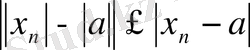 теңсіздігі орындалатыны белгілі. Олай болса
теңсіздігі орындалатыны белгілі. Олай болса
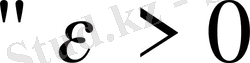 саны берілсе
саны берілсе
 ,
,
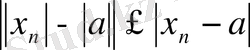
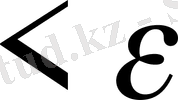 орындалатыны
орындалатыны
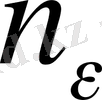 саны бар, яғни
саны бар, яғни
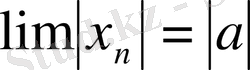
1. 2 Теңсіздіктерде шекке көшу
Теорема. Егер
 жағдайда
жағдайда
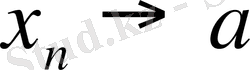 ,
,
 және де барлық
және де барлық
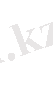
 нөмірлері үшін
нөмірлері үшін
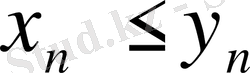 болса, онда
болса, онда
 . Қысқаша айтқанда, алынған теңсіздікте шекке көшуге болады.
. Қысқаша айтқанда, алынған теңсіздікте шекке көшуге болады.
Дәлелдеуі
.
Қарсы жорып,
a>b
дейік.
 санын мына аралықтан 0<
санын мына аралықтан 0<
 <
<
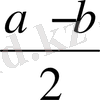 таңдап алайық. Тізбек шегінің анықтамасы бойынша осы
таңдап алайық. Тізбек шегінің анықтамасы бойынша осы
 санына сәйкес натурал
санына сәйкес натурал
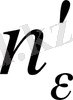 саны табылып, барлық
саны табылып, барлық
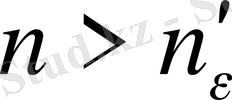 нөмірлері үшін
нөмірлері үшін
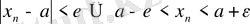 теңсіздігі орындалады. Осыған ұқсас түрде алынған
теңсіздігі орындалады. Осыған ұқсас түрде алынған
 санына сәйкес натурал
санына сәйкес натурал
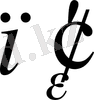 саны табылып, барлық
саны табылып, барлық
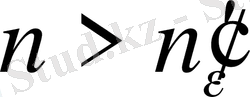 нөміллері үшін
нөміллері үшін
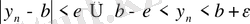 теңсіздігі орындалады. Егер
теңсіздігі орындалады. Егер
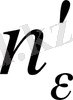 және
және
 сандарының ең үлкенін
сандарының ең үлкенін
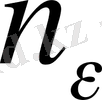 арқылы белгілесек, онда
арқылы белгілесек, онда
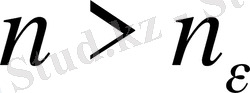 нөмірлері үшін осы теңсіздіктердің екеуі де сөзсіз орындалады. Сонда
нөмірлері үшін осы теңсіздіктердің екеуі де сөзсіз орындалады. Сонда
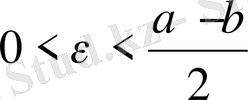 теңсіздігін түрлендіре келе, табатынымыз:
теңсіздігін түрлендіре келе, табатынымыз:
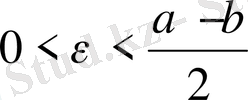
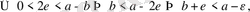
яғни
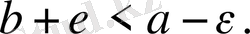
Барлық
 нөмірлері үшін соңғы теңсіздіктерден
нөмірлері үшін соңғы теңсіздіктерден
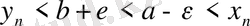 , нeмесе
, нeмесе
 теңсіздігі шығады. Алайда, бұл теңсіздік теореманың шарты
теңсіздігі шығады. Алайда, бұл теңсіздік теореманың шарты
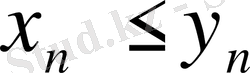 теңсіздігіне қайшы. Демек,
a>b
деп жору қате. Сондықтан
теңсіздігіне қайшы. Демек,
a>b
деп жору қате. Сондықтан
 болады ( яғни теңсіздікте шекке көшуге болады) .
болады ( яғни теңсіздікте шекке көшуге болады) .
- салдар. Егержағдайдажәне барлықнөмірлері үшінболса ондатеңсіздігі орындалады. Бұған көз жеткізу шекке көшсек жеткілікті
- салдар. Егер барлық мүшелерікесіндісіне тиісті болса, онда оның шегіссаны да осы кесіндіге тиісті болады. Шынында да,, теңсіздігінде шекке көшсек, іздегентеңсіздігі шығады. Ендіжәнетеңсіздіктері барлықнөмірлері үшін емес, қандай болса да бірнөмірінен артық барлықүшін орындалғанда да жоғарыда дәлелденген теорема мен одан шығатын бірінші салдардың дүрыс болып қала беретіндігін ескертеміз.
- Функция шегі теоремаларын сыныптан тыс жүйелі түсіндіруФункция шегінің екі анықтамасы және олардың пара - парлығы
ɑ нүктесінің қандай болмасын (с, d) маңайында ( мүмкін ɑ нүктесінде де ) анықталған ƒ функциясын қарастырайық.
1-анықтама. Егер a санына жинақталатын кез келген
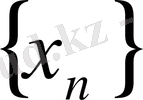 тізбегі (мұның ешбір элементі
тізбегі (мұның ешбір элементі
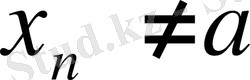 ) үшін ƒ функциясы мәндерінің сәйкес
) үшін ƒ функциясы мәндерінің сәйкес
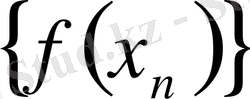 тізбегі
тізбегі
 санына жинақталатын болса, онда A санын ƒ функциясының
санына жинақталатын болса, онда A санын ƒ функциясының
 -
тің ɑ
-
ға ұмытылғандағы шегі деп атайды және былай белгілейді:
-
тің ɑ
-
ға ұмытылғандағы шегі деп атайды және былай белгілейді:
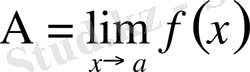
немесе
 жағдайда
жағдайда
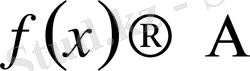 (символдар арқылы:
(символдар арқылы:
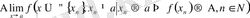 ) .
) .
2-анықтама. Егер кез келген
 санына сәйкес
санына сәйкес
 саны табылып,
саны табылып,
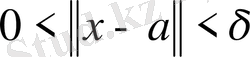 шартын қанағаттандыратын барлық
шартын қанағаттандыратын барлық
 үшін
үшін
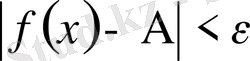 тенсіздігі орындалса, онда
тенсіздігі орындалса, онда
 санын ƒ функциясының
санын ƒ функциясының
 -тің ɑ
-
ға ұмтылғандағы шегі деп атайды және (1) өрнегімен белгілейді (символдар арқылы:
-тің ɑ
-
ға ұмтылғандағы шегі деп атайды және (1) өрнегімен белгілейді (символдар арқылы:
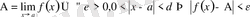 ) . Егер нүкте маңайының (жеке жағдайда ортасынан тесілген ) белгілеуін пайдалансақ, былай жазуға болады:
) . Егер нүкте маңайының (жеке жағдайда ортасынан тесілген ) белгілеуін пайдалансақ, былай жазуға болады:
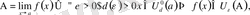
яғни кез келген
 үшін
үшін
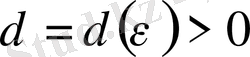 саны табылып, аргумент мәндері ɑ нүктесінің ортасынан (тесілген)
саны табылып, аргумент мәндері ɑ нүктесінің ортасынан (тесілген)
 маңайына тиісті болғанда ƒ функциясының сәйкес мәндері
маңайына тиісті болғанда ƒ функциясының сәйкес мәндері
 нүктесінің
нүктесінің
 маңайына (yөсі бойында) тиісті болады. Енді осы екі анықтаманың пара
-
парлығын дәлелдейік.
маңайына (yөсі бойында) тиісті болады. Енді осы екі анықтаманың пара
-
парлығын дәлелдейік.
1
-
анықтамада айтылған мағынада
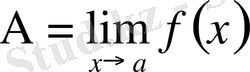 болсын, сонда осы шектің 2
-
анықтамада айтылған мағынада да бар болатынын көрсетейік. Қарсы жорып, екінші анықтама дұрыс болмайды дейік. Бұл жорамалды әдеткі
болсын, сонда осы шектің 2
-
анықтамада айтылған мағынада да бар болатынын көрсетейік. Қарсы жорып, екінші анықтама дұрыс болмайды дейік. Бұл жорамалды әдеткі
 символын
символын
 символымен,
символымен,
 символын
символын
 символымен, яғни, "барлық
символымен, яғни, "барлық
 үшін" сөз тіркесін "
үшін" сөз тіркесін "
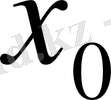 мәні табылады" сөз тіркесімен алмастыра отырып, керісінше тұжырымдап, 2
-
анықтаманы теріске шығарайық.
мәні табылады" сөз тіркесімен алмастыра отырып, керісінше тұжырымдап, 2
-
анықтаманы теріске шығарайық.
Сонда
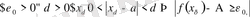 немесе
немесе
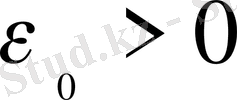 саны табылып, кез келген
саны табылып, кез келген
 саны үшін ең болмағанда бір
саны үшін ең болмағанда бір
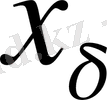 нүктесін табуға болады және
нүктесін табуға болады және
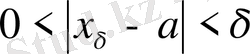 тенсіздігі орындалғанда
тенсіздігі орындалғанда
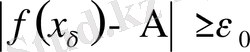 тенсіздігіде орындалады.
тенсіздігіде орындалады.
 саны үшін
саны үшін
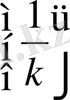 ,
,
 тізбегінің барлық мүшелерін алайық. Сонда әрбір
тізбегінің барлық мүшелерін алайық. Сонда әрбір
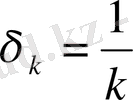 және оған сәйкес
және оған сәйкес
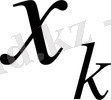 нүктесі үшін
нүктесі үшін
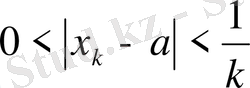 теңсіздігінен
теңсіздігінен
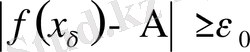 теңсіздігі шығады. Алайда
теңсіздігі шығады. Алайда
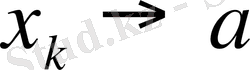 жағдайда оған функция мәндерінің
жағдайда оған функция мәндерінің
 тізбегі
тізбегі
 санына ұмтылмайды. 1
-
анықтаманың мағынасына қарсы осы табылған қайшылық айтылған болжамды дәлелдейді.
санына ұмтылмайды. 1
-
анықтаманың мағынасына қарсы осы табылған қайшылық айтылған болжамды дәлелдейді.
Енді 2
-
анықтамада
 тілінде айтылған мағынадағы ƒ функциясы шегінің 1
-
анықтамада айтылған мағынада да бар болатынын көрсетеміз. Ол үшін
тілінде айтылған мағынадағы ƒ функциясы шегінің 1
-
анықтамада айтылған мағынада да бар болатынын көрсетеміз. Ол үшін
 санын тағайындап алып, оған сәйкес
санын тағайындап алып, оған сәйкес
 санын табамыз. Енді
санын табамыз. Енді
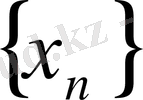
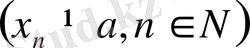 ұмтылатын қандайда да болсын тізбек дейік (
ұмтылатын қандайда да болсын тізбек дейік (
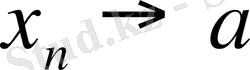 ) . Сонда
) . Сонда
 санына (жоғарыда тауып алған) сәйкес
санына (жоғарыда тауып алған) сәйкес
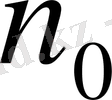 нөмері табылып, барлық
нөмері табылып, барлық
 үшін
үшін
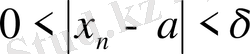 теңсіздігі орындалады. Бұдан 2
-
анықтама бойынша
теңсіздігі орындалады. Бұдан 2
-
анықтама бойынша
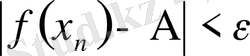 теңсіздігі шығады. Сонымен
теңсіздігі шығады. Сонымен
 жағдайда
жағдайда
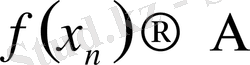 болады. Демек, функция шегінің екі анықтамасы бір-бірімен пара-пар болып шықты. Бұл екі анықтаманың қай-қайсысын да қолайлы болған кезде падалана беруге болады.
болады. Демек, функция шегінің екі анықтамасы бір-бірімен пара-пар болып шықты. Бұл екі анықтаманың қай-қайсысын да қолайлы болған кезде падалана беруге болады.
2. 2 Бір жақты шектер.
ƒ функциясы (с, d] жарты интервалда (мүмкін ɑ ϵ (с, d] нүктесінде де) анықталған дейік. 1-анықтама. Егер ɑ санына жинақталатын кез келген
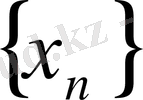 , мұндағы
, мұндағы
 ,
,
 , тізбегіне ƒ функция мәндерінің сәйкес
, тізбегіне ƒ функция мәндерінің сәйкес
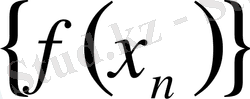
тізбегі
 санына жинақталатын болса, онда
санына жинақталатын болса, онда
 саны
саны
 -тің ɑ -ға ұмтылғандағы ƒ функциясының сол жақты шегі деп аталады және былай жазылады:
-тің ɑ -ға ұмтылғандағы ƒ функциясының сол жақты шегі деп аталады және былай жазылады:
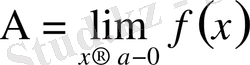
(символдар арқылы:
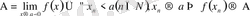 ) .
) .
2-анықтама. Егер кез келген
 үшін оған тәуелді
үшін оған тәуелді
 саны табылып,
саны табылып,
 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
 үшін
үшін
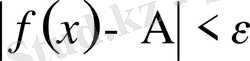 теңсіздігі орындалса, онда A саны x-тің ɑ -ға ұмтылғандағы ƒ функциясының сол жақ шегі деп аталады және былай жазылады:
теңсіздігі орындалса, онда A саны x-тің ɑ -ға ұмтылғандағы ƒ функциясының сол жақ шегі деп аталады және былай жазылады:
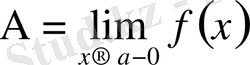 (символдар арқылы:
(символдар арқылы:
 ) .
) .
1 және 2-анықтамалардың мәндестігін 1-пункттегідей дәлелдеуге болады. Жоғары келтірілген анықтамаларға ұқсас түрде
 -тің ɑ -ға ұмтылғандағы ƒ функциясының оң жақ шегінің 1 және 2-анықтамаларын тұжырымдауға болады. Ол шекті
-тің ɑ -ға ұмтылғандағы ƒ функциясының оң жақ шегінің 1 және 2-анықтамаларын тұжырымдауға болады. Ол шекті
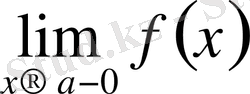 арқылы жазып көрсетейік
арқылы жазып көрсетейік
1.
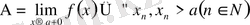
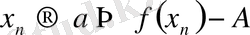
2.

Егер
ɑ=0
болса, онда
 орнына
орнына
 деп, ал
деп, ал
 орнына
орнына
 деп жазады.
деп жазады.
Теорема.
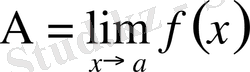 болуы үшін
болуы үшін
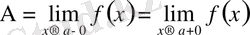
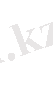 болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
Дәлелдеуі. Қажеттілік.
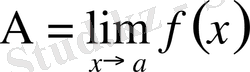 деп алайық. 2-анықтама бойынша, кез келген
деп алайық. 2-анықтама бойынша, кез келген
 үшін
үшін
 саны табылып,
саны табылып,
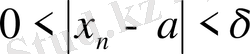 теңсіздігін қанағаттандыратын барлық x үшін
теңсіздігін қанағаттандыратын барлық x үшін
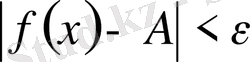 теңсіздігі орындалады. Бұдан шығатыны:
теңсіздігі орындалады. Бұдан шығатыны:
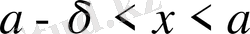 және
және
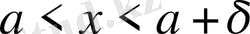 теңсіздіктерін қанағаттандыратын
теңсіздіктерін қанағаттандыратын
барлық
 үшін
үшін
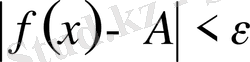 теңсіздігі орындалады, яғни
теңсіздігі орындалады, яғни
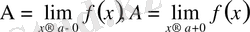 .
.
Жеткіліктік.
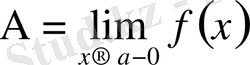 және
және
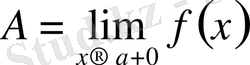 деп алайық. Сонда кез келген
деп алайық. Сонда кез келген
 үшін
үшін
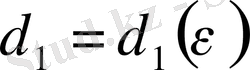 және
және
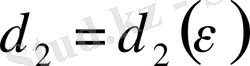 сандары табылып,
сандары табылып,
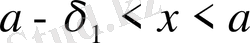 және
және
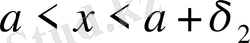 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық
 үшін
үшін
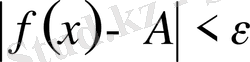 теңсіздігі орындалады. Енді
теңсіздігі орындалады. Енді
 және
және
 сандарының ең кішісін
сандарының ең кішісін
 деп белгілесек, онда
деп белгілесек, онда
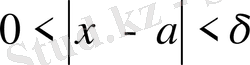 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
 үшін
үшін
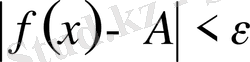 теңсіздігі шығады, яғни
теңсіздігі шығады, яғни
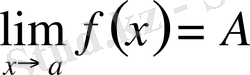 .
.
Ескерту.
 -тің ɑ-ға ұмтылғандағы ƒ функциясының бір жақты шектерін сол функцияның ɑ нүктесіндегі бір жақты шектерді деп те атайды және былай белгілейді:
-тің ɑ-ға ұмтылғандағы ƒ функциясының бір жақты шектерін сол функцияның ɑ нүктесіндегі бір жақты шектерді деп те атайды және былай белгілейді:
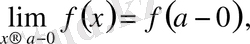
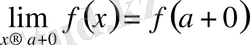
2. 3Функцияның шексіздіктегі шегі.
Алдыңғы пунктте келтірілген 1 және 2-анықтамаларда ɑ мен A сандары арқылы болатын. Енді біз аргумент тұрақты таңбалы шексіздікке ұмытылғандағы функция шегінің анықтамасын тұжырымдаймыз. ƒ функциясы
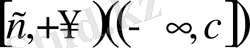 сәулесінде анықталған болсын.
сәулесінде анықталған болсын.
3-анықтама. Егер мүшелері белгілі бір нөмірден бастап оң (теріс) сан болатын аргумент мәндерінің кез келген ақырсыз үлкен
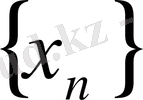 тізбегі үшін ƒфункциясының сәйкес мәндерінің
тізбегі үшін ƒфункциясының сәйкес мәндерінің
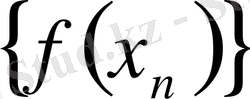 тізбегі A санына жинақталатын болса, онда A саны
тізбегі A санына жинақталатын болса, онда A саны
 оң (теріс) шексіздікке ұмтылғандағы ƒ функциясының шегі деп аталады және былай белгіленеді:
оң (теріс) шексіздікке ұмтылғандағы ƒ функциясының шегі деп аталады және былай белгіленеді:
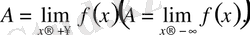 4-анықтама. Егер кез келген оң
4-анықтама. Егер кез келген оң
 саны үшін
саны үшін
 саны табылып,
саны табылып,
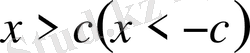 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 -тің барлық мәндері үшін
-тің барлық мәндері үшін
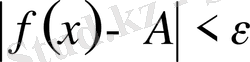 теңсіздігі орындалса, онда A саны
теңсіздігі орындалса, онда A саны
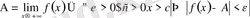 оң (теріс) шексіздікке ұмтылғандағы ƒ функциясының шегі деп аталады. (символдар арқылы:
оң (теріс) шексіздікке ұмтылғандағы ƒ функциясының шегі деп аталады. (символдар арқылы:
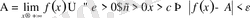
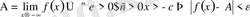 ) .
) .
Шегі бар функцияның шенделгендігі.
Егер функция шегінің тізбек шегі түсінігіне негізделген анықтамаларымен пайдаланатын болсақ (1 және 2-анықтамалар), онда функцияның шенделгендігі дәлелденді деп санауға болады; (шынында да, кез келген
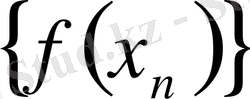 жинақталатын тізбек болып табылады) . Бұл тұжырымды функция шегінің 2 және 4-анықтамаларын пайдалана отырып тексерейік.
жинақталатын тізбек болып табылады) . Бұл тұжырымды функция шегінің 2 және 4-анықтамаларын пайдалана отырып тексерейік.
Теорема. Егер
 -тің
ɑ
-ға ұмтылғандағы ƒ функциясының шегі
A
саны бар болса, онда ƒ функциясы ɑ нүктесінің белгілі бір маңайында(мүмкін ɑ нүктесінде де) шенделген болады (символдар арқылы:
-тің
ɑ
-ға ұмтылғандағы ƒ функциясының шегі
A
саны бар болса, онда ƒ функциясы ɑ нүктесінің белгілі бір маңайында(мүмкін ɑ нүктесінде де) шенделген болады (символдар арқылы:
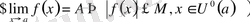 ) .
) .
Дәлелдеуі.
 -
тің
ɑ
-
ға ұмтылғандағы ƒ функциясының A-ға тең шегі бар болуы кез келген
-
тің
ɑ
-
ға ұмтылғандағы ƒ функциясының A-ға тең шегі бар болуы кез келген
 санына сәйкес
санына сәйкес
 саны табылып,
саны табылып,
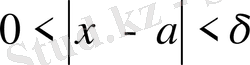 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
 үшін
үшін
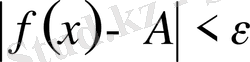 теңсіздігінің орындалуымен пара-пар болады.
теңсіздігінің орындалуымен пара-пар болады.
Енді
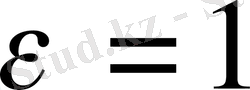 деп алайық. Соңғы теңсіздікті, айырым модулінің қасиетін пайдалана отырып, былай жазайық:
деп алайық. Соңғы теңсіздікті, айырым модулінің қасиетін пайдалана отырып, былай жазайық:
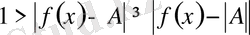 . Бұдан
. Бұдан
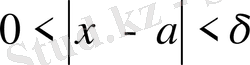 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
 -тер үшін
-тер үшін
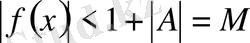 теңсіздігі орындалатыны шығады. Осыған
теңсіздігі орындалатыны шығады. Осыған
ұқсас теорема
 жағдайында шегі бар болатын ƒ функциясы үшін де дұрыс болады. ƒ функциясының шенделгендігін ақырсыз қашықтықтағы нүкте маңайында орналасқан барлық
жағдайында шегі бар болатын ƒ функциясы үшін де дұрыс болады. ƒ функциясының шенделгендігін ақырсыз қашықтықтағы нүкте маңайында орналасқан барлық
 үшін де (яғни, барлық
үшін де (яғни, барлық
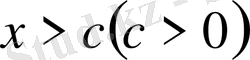 , немесе
, немесе
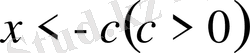 үшін) дәлелдеуге болады. Мұның дәлелдемесі жоғарыда келтірілген теореманың дәлелдемесін сөзбе-сөз дерлік қайталайды. Сонымен,
үшін) дәлелдеуге болады. Мұның дәлелдемесі жоғарыда келтірілген теореманың дәлелдемесін сөзбе-сөз дерлік қайталайды. Сонымен,
 -тің
ɑ
-ға ұмтылғанда (немесе
-тің
ɑ
-ға ұмтылғанда (немесе
 жағдайда) ƒ функциясының арқылы шегі бар болса, онда ол функция
ɑ
нүктесінің қандай болса да бір маңайында шенделген болуы қажетті.
жағдайда) ƒ функциясының арқылы шегі бар болса, онда ол функция
ɑ
нүктесінің қандай болса да бір маңайында шенделген болуы қажетті.
Функция шектері туралы теоремалар.
Бұл пунктте функцияларға арифметикалық амалдар қолдану жөнінде әңгімеленеді. Қарастырылатын барлық функциялар да қандай болса да бір интервалында (ақырлы немесе ақырсыз) ( мүмкін
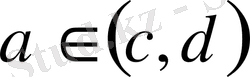 нүктесінде де) анықталған деп санаймыз. Егер
ɑ = с
немесе
ɑ = d
болса, онда қарастырылып отырған функция шегі сәйкес оң жақты немесе сол жақты шек деп түсініледі. Бұған қоса
нүктесінде де) анықталған деп санаймыз. Егер
ɑ = с
немесе
ɑ = d
болса, онда қарастырылып отырған функция шегі сәйкес оң жақты немесе сол жақты шек деп түсініледі. Бұған қоса
 немесе
немесе
 жағдайлары да қарастырылуы мүмкін. Функция сәйкес ақырсыз қашықтық тағы маңайында анықталған болады.
жағдайлары да қарастырылуы мүмкін. Функция сәйкес ақырсыз қашықтық тағы маңайында анықталған болады.
1-теорема. Егер
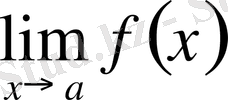 және
және
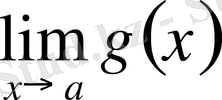 шекткрі бар болса, онда
шекткрі бар болса, онда
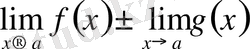 шегі де бар болады және мына теңдік орындалады:
шегі де бар болады және мына теңдік орындалады:
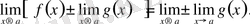
Бұл теорема қосылғыштар саны шектеулі болған жағдай үшін де орындалады.
2- теорема. Егер
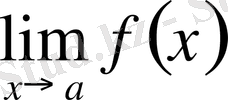 және
және
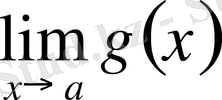 шектері бар болса, онда
шектері бар болса, онда
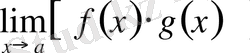 шегі де бар болады және теңдік орындалады:
шегі де бар болады және теңдік орындалады:
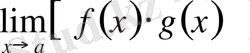 =
=
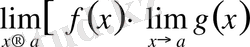
Ескерту. Егер
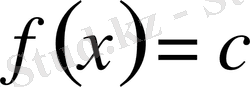 (тұрақты сан) болса, онда
(тұрақты сан) болса, онда
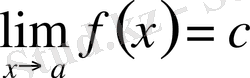 .
.
1-салдар. Егер
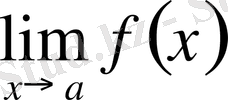 бар болса, онда кез келген с саны үшін
бар болса, онда кез келген с саны үшін
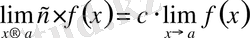 .
.
2-салдар
.
Егер
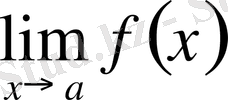 бар болып,
бар болып,
 - натурал сан болса, онда
- натурал сан болса, онда
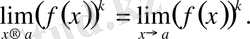
3-теорема
.
Егер
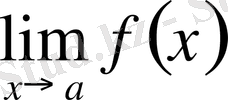 және
және
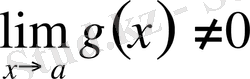 шектері бар болса, онда
шектері бар болса, онда
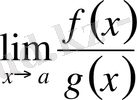 шегі де бар болады және
шегі де бар болады және
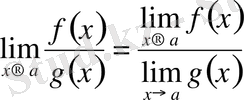 теңдігі орындалады.
теңдігі орындалады.
Бұл теоремалардың барлығы да тізбек шектері үшін дәлелденген сәйкес теоремаларды пайдалана отырып дәлелденеді.
Ақырсыз кіші және ақырсыз үлкен функциялар.
Бұл пунктте қарастырылатын барлық функциялар қандай болса да бір
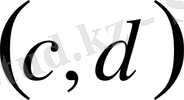 интервалында ( ақырлы және ақырсыз) , (мүмкін
интервалында ( ақырлы және ақырсыз) , (мүмкін
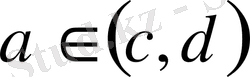 нүктесінде де анықталған деп санаймыз. Егер ɑ = с немесе ɑ = d болса, онда функцияның сәйкес шектерін оң жақты немесе сол жақты шектер деп түсіну керек.
нүктесінде де анықталған деп санаймыз. Егер ɑ = с немесе ɑ = d болса, онда функцияның сәйкес шектерін оң жақты немесе сол жақты шектер деп түсіну керек.
Анықтама. Егер
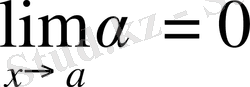 болса, онда
болса, онда
 жағдайда
жағдайда
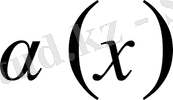 ақырсыз кіші функция деп аталады.
ақырсыз кіші функция деп аталады.
Ақырсыз кіші функция түсінігін пайдаланып функция шегінің тағы бір анықтамасын мына теорема түрінде беруге де болады.
Теорема.
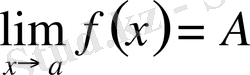 теңдігі орындалуы үшін
теңдігі орындалуы үшін
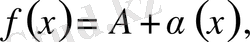 мұндағы
мұндағы
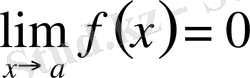 , теңдігінің орындалуы қажетті және жеткілікті (символдар арқылы:
, теңдігінің орындалуы қажетті және жеткілікті (символдар арқылы:
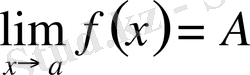

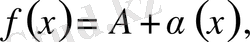 ) . Ақырсыз кіші функциялардың мына қасиеттерін келтірейік.
) . Ақырсыз кіші функциялардың мына қасиеттерін келтірейік.
1-лемма.
 жағдайда саны шектеулі ақырсыз кіші функциялардың алгебралық қосындысы да
жағдайда саны шектеулі ақырсыз кіші функциялардың алгебралық қосындысы да
 жағдайда ақырсыз кіші функция болады
жағдайда ақырсыз кіші функция болады
2-лемма.
 жағдайда ақырсыз кіші
жағдайда ақырсыз кіші
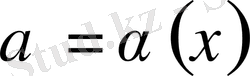 функциясы мен ɑ нүктесі маңайында шенделген
функциясы мен ɑ нүктесі маңайында шенделген
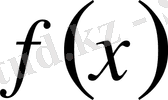 функциясының
функциясының
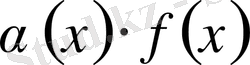 көбейтіндісі де
көбейтіндісі де
 жағдайда ақырсыз кіші функция болады.
жағдайда ақырсыз кіші функция болады.
Салдар.
 жағдайда саны шектеулі ақырсыз кіші функциялардың көбейтіндісі де ақырсыз кіші функция болады. Бұл қасиеттердің барлығы да функция шегінің тізбектер түсінігіне негізделген 1-анықтамасымен ақырсыз кіші тізбектер үшін келтірілген сәйкес леммаларға сүйеніп дәлелденді.
жағдайда саны шектеулі ақырсыз кіші функциялардың көбейтіндісі де ақырсыз кіші функция болады. Бұл қасиеттердің барлығы да функция шегінің тізбектер түсінігіне негізделген 1-анықтамасымен ақырсыз кіші тізбектер үшін келтірілген сәйкес леммаларға сүйеніп дәлелденді.
Алдыңғы пункттегі 1-3 теоремаларды жоғарыдағы теорема мен 1-2-леммаларды пайдаланып дәлелдеуге болатындығын ескертеміз. Ақырсыз кіші функциялар түсінігімен қатар ақырсыз үлкен функциялар түсінігі де жиі қолданыла береді.
 жағдайдағы ақырсыз үлкен функцияның бір анықтамасын келтірейік.
жағдайдағы ақырсыз үлкен функцияның бір анықтамасын келтірейік.
Анықтама. Егер кез келген
 саны үшін
саны үшін
 саны табылып,
саны табылып,
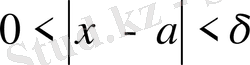 шартын қанағаттандыратын барлық
шартын қанағаттандыратын барлық
 үшін
үшін
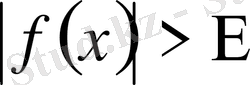 теңсіздігі орындалса, онда ƒ функциясы
теңсіздігі орындалса, онда ƒ функциясы
 жағдайда ақырсыз үлкен функция деп аталады және былай жазылады:
жағдайда ақырсыз үлкен функция деп аталады және былай жазылады:
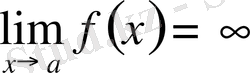
Осыған ұқсас түрде ɑ нүктесінің сол жағындағы не оң жағындағы тұрақты таңбалы ақырсыз үлкен функция анықтамасын тұжырымдап айтуға болады. Оларды былай жазады:
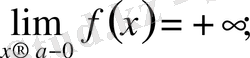
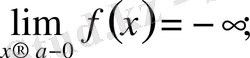
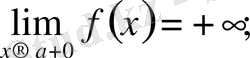
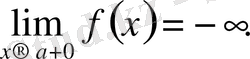
Енді ақырсыз кіші функциялар мен ақырсыз үлкен функциялар арасындағы қарапайым байланысты атап өтейік.
Теорема. Егер
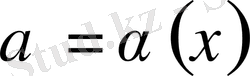 функциясы
функциясы
 жағдайдағы ақырсыз кіші және
жағдайдағы ақырсыз кіші және
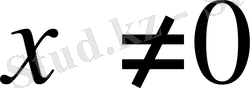 үшін
үшін
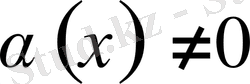 болса, онда
болса, онда
 жағдайда
жағдайда
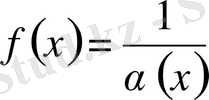 функциясы ақырсыз үлкен болады.
функциясы ақырсыз үлкен болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz