Дирихле принципі туралы жалпы ақпарат

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Дирихле принципі туралы жалпы ақпарат

Дирихле Вестфалия қаласында почтмейстердің отбасында дүниеге келген. 12 жасында Дирихле Бонндағы гимназияда, екі жылдан кейін Кельндегі иезуит гимназиясында оқыды, онда оған неміс физигі Георг Ом білім берді. 1822 жылдан 1827 жылға дейін ол Парижде үй мұғалімі ретінде өмір сүрді, онда ол Фурье шеңберін зерттеумен айналысты. 1825 жылы Дирихле А. Легандрмен бірге N=5 нақты жағдайға арналған Ферманың үлкен теоремасын дәлелдеді. 1827 жылы Жас жігіт Александр фон Гумбольдттың шақыруымен Бреслау университетінің приват-доценті қызметіне орналасады. 1829 жылы ол Берлинге көшіп, онда үздіксіз 26 жыл жұмыс істеді, алдымен доцент, содан кейін 1831 жылдан бастап ерекше, ал 1839 жылдан бастап Берлин университетінің қарапайым профессоры болды. 1831 жылы Дирихле әйгілі композитор Феликс Мендельсон-Бартольдидің қарындасы Ребекка Мендельсон-Бартольдиге үйленді.

Дирихле математиканың әртүрлі салаларында, сонымен қатар механика мен математикалық физикада бірқатар үлкен ашылуларға ие. 1855 жылы Дирихле Гаусстың мұрагері ретінде Геттинген университетінің Жоғары математика профессоры болды. Оның жетістіктерінің бірі-Фурье қатарларының жақындасуының дәлелі.

Көптеген есептерді шешу үшін, логикалық әдістер қолданылады. Біз оның бір түрі - Дирихле принципін қарастырайық. Дирихле принципін оқып үйрену арқылы әр түрлі логикалық есептерді, олимпиадалық есептерді оңай шешуге болады. Бұл қарапайым принципті бірінші болып неміс математигі Лежен Дирихле (1805-1859) тұжырымдаған.

Дирихле принципі екі жиын арасындағы қатынасты өрнектейді. Дирихле принципін үйрену үшін бірнеше сабақ өткізу қажет. Дирихле принципін қосымша сабақтарда да үйретуге болады, себебі ол олимпиадалық есептерді шешуде жиі қолдаланылады. Дирихле принципінің негізгі ерекшелігі есептің конструктивті емес жолын беруде, яғни тор не екенін білеміз, бірақ оның қайда орналасқанын нақты айту қиын. Ал конструктивті шешімін табу қиындықтар туғызуы мүмкін. Дирихле принципінің негізгі анықтамасы: n торда m қоян отыр және n ˃ m болса, онда ең болмағанда 1 бос тор көз табылады.

Дирихле принципінің ең кең тараған тұжырымдамасы:

Егер қояндардың саны торлардың санынан артық болып қояндарды торларға орналастыру керек болса, онда кем дегенде бір торда қояндардың саны 1-ден артық болатындай орналастыруға болады. (1-суретте көрсетілгендей)

Image result for принцип Дирихле

1-сурет

2012 жылы жарық көрген авторы Ә. Н. Шыныбековтың 8 сынып алгебрасының Натурал сандар тарауының §6-ы осы Дирихле принципіне арналған. Осы тақырыпта мынадай мысал келтірілген:

Мысал. Кез келген 13 оқушының ішінен туған айлары бірдей кем дегенде екі оқушы табылатынын көрсетейік.

Шешуі. Шынында да, барлығы 12 ай болғандықтан, 13 оқушының кем дегенде екеуі бір айда туады. Мұнда «үйшіктер» - 12 ай, «қояндар» - 13 оқушы.

Енді осы тақырыпқа байланысты оқушыларға шығаруға берілген есептерді қарастырайық:

778. Дүкенге алманың үш сортынан 10 қорап алма әкелінді. Әрбір қорапқа алманың тек бір ғана сорты салынған. Алманың бірдей сорты салынған 4 қорап табыла ма?

Шешуі. Мұндай есепті шығаруда оқушыға жай ғана Дирихле принципін білу жеткіліксіз. Логикалық ойлауды талап етеді. Мұндағы «Үйшіктер» - 10 қорап, ал «қояндар» - үш сортты алмалар. Ендеше Дирихле принципі бойынша әр 3қорапта бір сорт, сонда 1 қорап артық қалады. Демек осы қорапта үш сортты алманың кез келген біреуі болуы мүмкін. Демек кез келген сортты алмалардың біреуі 4 қорапқа салынған.

Жоғарыда көрсетілген мысалдардан тыс Дирихле принципін қолдана отырып шығаруға болатын есептерді мазмұнына қарай мынадай бірнеше топтарға жіктеуге болады:

Геометриялық есептер;
Жұптауға берілген тапсырмалар;
Танысу мен туған күндерге арналған тапсырмалар;
Арифметикалық орта есептер;
Бөлінгіштікке арналған есептер;
Комбинаторикаға тапсырмалар;
Сандар теориясына арналған есептер;

1 - тапсырма. Қабырғасы 1 см болатын теңқабырғалы үшбұрыштың ішінде 5 нүкте орналасқан. Кейбір екі нүктенің арақашықтығы 0, 5 см-ден кем болатынын дәлелдеңдер. (Геометриялық есеп)

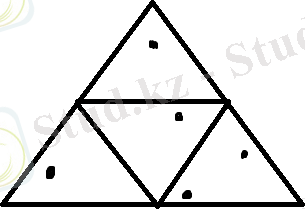
Шешуі. Теңқабырғалы үшбұрыштың орта сызықтары оны қабырғалары 0, 5 см болатын бірдей төрт үшбұрышқа бөледі. Пайда болған үшбұрышты - «үйшіктер» десек, онда нүктелер - «қояндар» болады. Дирихле принципі бойынша кем дегенде екі нүкте бір үшбұрыштың ішінде болады. Яғни осы екі нүктенің арасы 0, 5 см- ден кем болады.

* Мұнда үшбұрыштың ішінде орналасқан кесіндінің ұзындығы оның ең үлкен қабырғасының ұзындығынан аз болатындығы туралы белгілі лемма қолданылады.

2 - тапсырма. Орманда миллион шырша бар. Олардың әрқайсысындағы инелер саны 600 000-нан аспайтыны белгілі. Орманда инелер саны бірдей болатын екі шырша табылатынын дәлелдеңдер. (Жұптауға арналған есеп)

Шешуі. Шыршалар - «қояндар», ал шыршадағы инелер саны: 0, 1, 2, 3, . . . , 6 - «ұяшықтар» болсын. «Ұяшықтар» саны 61, ал «қояндар» 1. Мұнда «қояндар» «ұяшықтардан» әлдеқайда көп. Онда Дирихле принципі бойынша қандай да бір «ұяшықта» кем дегенде екі «қоян» болады. Яғни, бір «ұяшықта» екі «қоян» отырса, онда бұл шыршалардағы инелер саны бірдей.

3 - тапсырма. 12 бүтін сан берілген. Олардың ішінен айырмасы 11-ге бөлінетіндей екі санды таңдап алуға болатынын дәлелде. ( Бөлінгіштікке арналған есеп)

Шешуі. Бүтін сандар-«қояндар», олардың саны 12, онда торлардың саны 12-ден аз болу керек. «торлар»- бұлар бүтін сандарды 11-ге бөлгендегі қалдықтар. Барлық «торлар» саны 11 болады: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Онда Дирихле принципі бойынша бір торда 2 қоян отыратындай кем дегенде бір тор табылады. Яғни қалдықтары бірдей болатындай екі бүтін сан табылады. Ал 11-ге бөлгенде бірдей қалдық қалатын екі санның айырмасы 11-ге бөлінеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.