Жанармай станциясының қызмет көрсетуін математикалық және компьютерлік модельдеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 31 бет
Таңдаулыға:
Мазмұны
КІРІСПЕ
I Модель және компьютерлік моделдеу негіздері
1. 1 Модель және оның этаптары
1. 2 Модель түрлері
1. 3 Математикалық модель
II ЖАНАРМАЙ СИАНЦИЯСЫНЫҢ ЖҰМЫСЫНЫҢ МОДЕЛІ.
2. 1 Модельденетін объекттің сипаттамасы
2. 2 Есептің қойылымы
2. 3 Жүйенің концептуалды моделі
2. 4 Жүйенің модельдеуші алгоритмі
III СТАНЦИЯНЫҢ қызмет көрсетуі мен дамуын модельдеу
3. 1 Машиналық эксперимент жоспары және оны жүргізу
3. 2 Компьютермен модельдеу нәтижелерін талдау
Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
"Модель" түсінігімен біз бала кезімізден таныспыз. Ойыншық автомобильдер, ұшақ және кеме көпшілігіміз үшін сүйікті ойыншықтарымыз болды. Баланың дамуына, қоршаған ортаны тану процесіне осындай, нақты объектінің моделі болып табылатын ойыншықтар маңызды роль атқарады.
Модельдің көптеген әртүрлі аныќтамалары бар. Физикада, экономикада, математикада немесе географияда модель туралы айтќанда оны ќандай маќсат үшін пайдалануға байланысты әртүрлі түсінуге болады.
Ќарапайым модельдер орта сыныптарда арифметикалыќ амалдардың ќасиеттерін оќу кезінде кездеседі. Кейінірек модельдер саны өсіп физика, география жєне т. б. пайда болды. Себебі практикалыќ жағынан кез келген ќұрал жабдыќтар (карта, глобус, кристалды тор жєне т. б. ) натуралды модель болып табылады. Олар зерттелетін объектілер, процестер мен ќұбылыстардың ең маңыздысын көрсетуге мүмкіндік береді. Модель міндетінің негізгісі осы.
Моделдеу ғылыми орталықтарда өзінің қолданыныс аясын кеңейтуде. Бірақ, моделдеу біраз жылдар бойы басқа ғылымдарға қосылмай жекеше дамыды. Өзгеше дамығандықтан жалпы терминологиядан, жалпы түсіну системасынан алшақта болды.
Модеьдеу жүйесі (modeling system) - зерттелетін жүйенің немесе оның элементтерінің математикалық және физикалық аналгтарын құру және талдау. Модельдік тәжшрибе зерттеу тәсілі ретінде жүйені жаңғыртуға және зерттеуге мүмкіндік береді, ал зерттелетін жүйеге тікелей тәжірибе жүргізу қиын немесе экологиялық тұрғыдан тиімсіз болуы мүмкін.
«Модель» термині көп мағыналы. Модельдеп қандай да бір заттың кішірейтілген көшірмесін (самолет моделі, тұрғын үйлер макеті), математикалық формулаларды, бұрыштан горизонтқа лақтырылған лақтырылған дененің ұшу моделін, іштен жану двигателі жұмысының моделін, қандай да бір нәрсенің эталонын (метр эталоны, килограм эталоны) айтамыз.
Қарастырылған моделдеу әдісінің маңыздылығы күйін және күрделі жүйе элементтерінің өзара әректін имитациялайтын арнайы алгоритмде компьютерде талдануыннан тұрады. Процесс уақытында кездейсоқ факторларға әсер ету моделдеу процессінде өңделінетін ықтималдық сипатпен берілген кездейсоқ сандар арқылы өндіріледі.
Компьютерлік модельдеу күрделі процесстерді зерттеуде әлдеқайда қолданылады және моделдеудің басқа түрлерінің алдында маңызды артықшылықты игереді. Оның негізгі артықшылығы болып едәуір күрделі есептерді шешу мүмкіндігі болып табылады: зерттелінетін жүйеде бір мезгілде үздіксіз және дискретті әрекеттер бар болуы мүмкін, күрделі табиғаттағы көпсанды кездейсоқ сандарға әсер етуі мүмкін, громоздикалық қатынастармен суреттелуіі мүмкін және т. б.
Компьютерлік моделдеу басқа да кез келген сандық әдіс бар кемшіліктерге ие болады, алынған шешім әрдайым жеке меншік сипатты алып жүреді. Бұл кемшіліктерге қарамастан компьютерлік моделдеу қазіргі уақытта күрделі жүйелерді зерттеуде анағұрлым әсерлі құрал болып табылады.
Компьютерлік моделдеудің маңызды ролі есепті шешу кезінде басқаруды автоматтандырумен байланысты жүргізіледі. Компьютерлік моделдеу көмегімен басқарудың әртүрлі принциптерінің әсерлілігі, басқарушы жүйелерді құру нұсқалары, сондай-ақ басқарушы аппаратураның сенімділігі мен жұмысқа қаблеттілігі бағалануы мүмкін.
Курстық жұмыстың тақырыбы «Жанармай станциясының жұмысын модельдеу».
Курстық жұмыстың мақсаты - Жанармай станциясының қызмет көрсетуі мен дамуын модельдеу болып табылады.
Жанармай станциясының жұмысын сипаттайтын мына шамаларды табу керек:
- автомобильдер кезегінің орташа ұзындығын;
- автомобильдердің кезек күту уақытының орта шамасын;
- автомобильдің жанармай станциясында тұрған орта уақыт;
- жанармай станциясы жабдықтарының бос тұрған орташа уақытын;
- жанармай станциясында тұрған автомобильдер орташа санын.
I Модель және компьютерлік моделдеу негіздері
1. 1 Моделдеу және оның этаптары
Обьектінің шартты бейнесі немесе кейбір обьектілі жүйелер(немесе процесс), өзімен бірге байланысты компьютерлік кестемен бейнеленген, блок-схема, диаграмма, графика, суреттер, анимациялық бейнелер, гипермәтіндер т. с. с және обьектінің элементтері арасындағы тікелей байланыстарын және бейнеленетін құрылымды біз структуралық - функционалдық моделдеу деп атаймыз.
Ғылыми танымның әдісі ретінде модельдеу элементтерімен оқушылар орта кластарда математика курсын оқуда танысады. Формула, сызба, теңдеу және т. б. моделдер мысалдары болып табылады.
Адамзат танымындағы кез келген Q1 және Q2 объектілерінің қандай да бір ұқсастығы мен айырмашылықтары болады.
Бірінші Q1 объектісі екінші Q2 объектісіне ауысқанда олардың белгілі бір ұқсастығы мен белгілі бір айырмашылығы болғанда ерекше мән беріледі. Бұл жағдайда Q1 - дің маңызды қасиеттерін Q2 - арқылы зерттеу мүмкіндігі пайда болады. Q2 объектісінің көмегімен Q1 объектісінің маңызды қасиеттерін зерттеу мен анықтау үшін Q1 объектісін Q2 объектісімен алмастыру - Q1 объектісін Q2 объектісі арқылы моделдеу деп аталады. Алмастырылушы (модельденуші) объект оригинал немесе натура деп, алмастырушы (модельденуші) - модель деп аталады. Модель - оригиналдың негізгі қасиеттерін анықтау мен зерттеуде қолданылатын баламасы. [19]
Демек, модель ќұру процесі модельдеу деп аталады. Наќтылы объектіні, ќұбылыс немесе процесті оған сәйкес көшірмесіне айырбастауды моделдеу деп түсінуге болады.
Моделдеу бірнеше этаптардан тұрады:
- Есептің қойылымы және объектінің зерттелетін маңызды қасиеттерін анықтау;
- Объектінің оригиналын зерттеудің қиындығы мен мүмкін еместігінің себептерін анықтау;
- Оригиналдың көптеген қасиеттерін қайталайтын және оңай зерттелетін модель таңдау;
- Модельді есептің қойылымы бойынша зерттеу;
- Модельді зерттеу нәтижелерін оригиналға ауыстыру;
- Нәтижелерді салыстыру.
1. 2 Модель түрлері
Классификациялау объектілерді жүйелеуде, оларды зерттеуді жеңілдетуде, терминологиясын реттеуде және ғылыми нәтижесін талдауда маңызды этап болып табылады.
Модельдерді төмендегідей классификациялауға болады:
Логикалық моделдер адамзат санасындағы логикалық заңдар арқылы пайда болады. Ол образдық және белгілік болып бөлінеді. Образды моделдер оригиналдың қасиеттерін оригинал элементтері немесе материалдық әлем элементтерін қайталайтын көптеген әлем элементтері арқылы зерттейді. Белгілік немесе символдық моделдер шартты белгілермен символдар (математикалық өрнектер мен теңдеулер, физикалық және химиялық формулалар) көмегімен оригинал қасиеттерін зерттейді.
Материалдық моделдер табиғаттың объективті заңдылықтары арқылы пайда болады. Оған функционалдық және геометриялық моделдерді жатқызуға болады.
Шартты модель оригиналдың қасиеттері мен қатынастарын белгілі бір шарттар мен келісімдер негізінде көрсетеді. Мұндай моделдің оригиналға сырттай ұқсастығы мүлдем болмауы мүмкін. Оған барлық белгілік және образды белгілік моделдер жатады.
Сәйкестік моделдерге сәйкестігіне байланысты оригиналға өтуге болатын ұқсас болу қасиеті жеткілікті. Яғни логикалық қорытынды бойынша моделде болатын кейбір қасиеттер оригиналда болуы мүмкін. Өйткені оригиналдың басқа қасиеттері модельдің қасиеттерімен бірдей болады.
Математикалық моделдер оригиналға өтуді, тиянақтылауды және қасиеттерін зерттеуді математикалық әдістер көмегімен жүргізеді. Математикалық моделдер есептік және сәйкестік болып екіге бөлінеді. Есептік моделдер оригинал қасиеттерін математикалық өрнектер, формулалар, теңдеулер, графиктер, кестелер және басқалар арқылы зерттейді. Сәйкестік моделдерде айнымалы шамалар оригиналдың математикалық тәуелділіктерімен анықталған айнымалы шамалармен тығыз байланысты болады.
Баламалық моделдер логикалық және баламалық болып егіге бөлінеді. Баламалық материалды моделдер аналогтық (үздіксіз, сандық, дискретті) және аналогты сандық (құрама және гибридті) болып бөлінеді. Олар сәйкесінше математикалық сипатына, яғни үздіксіз дискретті шамаларға байланысты болады. Соңғысын оригиналдың баламасы және материалдық моделі оригиналды сипаттайтын теңдеуді шешуге арналған есептеуіш құрылғы ретінде қолдануға болады.
1. 3 Математикалық модель
Ќуатты жылу станциясын ќаланынң жанынан соғуға бола ма? Егер соғатын болсаќ тұрғын аудандардың солтүстігі не ма, шығысына ма-? Немесе экологиялыќ катастрофа болдырмас үшін ќұрылыстан бас тарту керек па?
Адам шығармашылығы процесінде осы секілді көптеген сұраќтар пайда болады. Оларға көптеген ќаржыны талап ететін немесе адам өміріне ќауіпті табиғи зерттеулер көмегімен жауап алу мүлдем ќиын, ал кейде мүмкін болмайды. Ал зерттеуге мүмкін емес жер ќабатының астында немесе алыстағы космоста орналасќан объектерді ќалай зерттеуге болады? Мысалы, күннің түкпірінде немесе күн жүйесінің планеталарында ќандай процестер жүріп жатыр? Осы сияќты кейбір процестерді көзбен көріп, ќолмен ұстау мүлдем мүмкін емес.
Мұнда маманға ќоршаған болмысты оќытудың ерекше формасы - математикалыќ модель, яғни математикалыќ символдардан, ќатынастардан жєне операциялардан тұратын модель ќұру көмекке келеді.
Математикалыќ модель деп берілген өрнектермен бейнеленетін ќұбылыстарды беру тәсілін айтады.
Математикалық моделдер оригиналға өтуді, тиянақтылауды және қасиеттерін зерттеуді математикалық әдістер көмегімен жүргізеді. Математикалық моделдер есептік және сәйкестік болып екіге бөлінеді. Есептік моделдер оригинал қасиеттерін математикалық өрнектер, формулалар, теңдеулер, графиктер, кестелер және басқалар арқылы зерттейді. Сәйкестік моделдерде айнымалы шамалар оригиналдың математикалық тәуелділіктерімен анықталған айнымалы шамалармен тығыз байланысты болады.
Зертеу жұмысын мамандандырылып жүргізу үшін математика мен механиканың, физика мен химияның, экология мен экономиканың кіптеген білімдерін білу талап етіледі. Мұнда зерттеушінің негізгі ќұрылғысы электронды есептеу машинасы болып табылады. Бұл үшін маман математикалыќ модель облысында жоғары деңгейдегі алгоритмдік тілде программалаудың ќыры мен сырын меңгеруі ќажет.
Математика шындық дүниені тікелей физикалық объектілер арқылы емес, оның математикалық моделін жасап, тексеру арқылы зерттейді. Математикалық модельдеу болмыстық құбылысты таза күйінде, аса қажетті қасиеттері мен қырларын ғана қамтып, басқа қосалқы жағдайларына көңіл аудармай абстракті түрде бейнелеу.
Құбылысты математикаландыру үшін алдымен қажетті түсініктерге нақты дәл анықтамалар беріледі, олардың мәні мен сандық өлшемдері айқындалып, қандай айнымалы шамалармен қызметтес болатыны көрсетіледі. Бұдан соң айнымалылардың арасындағы функционалды байланыстардың, яғни зерттейтін құбылысқа тән объективті заңдылықтардың математикалық кескіндері табылады. Осындай математикаландырылған теория қалыптасқан соң алынған заңдылықтарға байланысты сандар мен қорытындыларды егжей - тегжейлі тексеру, бұл нәтижелерді басқа жәйттерге пайдалану мүмкіндігін қарастыру басталады. Бұл теория әр қадам сайын, қайта - қайта экспериментті сынақтан өтіп жасалған математикалық модельді әрі қарай дамытып, жетілдіре түседі. Бір керемет жері алынған нәтижелер мүмкіндігінше абстрактілі болғандықтан оларды пайдалану шеңбері мейлінше кең болады.
Математикалық модель объект қасиеттерін көрсететін математикалық сипаттаманың теңдеулер жүйесі болып табылады. Осы анықтама бойынша математикалық модель оның үш аспектісіне байланысты қарастырылуы тиіс. Олар мағыналық, аналитикалық және есептеуіш аспекттері.
Модельдің мағыналық жағы - формальды сипаттамасы моделдеуші объекттің физикалық табиғатын сипаттайды.
Аналитикалық жағы - моделдің әртүрлі параметрлерінің арасындағы функционалды қатыстары мен формалды сипатының теңдеулер жүйесі түрінде математика тіліндегі өрнегі.
Есептеуіш аспекті - моделдеуші алгоритм, математикалық модель параметрлерінің мәнін табу үшін қолданылатын математикалық сипаттамалар теңдеулерін шешуге арналған операциялар тізбегі ретінде анықталады, яғни моделдеу процесін алгоритмдейді.
Кез келген математикалық модель құру моделдеу объектісінің формальды сипаттамасынан басталады. Бұл кезде моделдеу көрсетілетін объектте жүріп жатқан қарапайым процестерді ерекшелеп, оларды сипаттау кезінде қолданылатын негізгі жорамалдар қалыптастырылады. Өз кезегінде қарапайым процестер тізбегі математикалық моделге қосылатын, оъектінің жағдайын сипаттайтын параметрлер байланысын анықтайды. Математикалық моделдеуде келесі параметрлер кластарын пажырата білу керек: конструктиті, физикалық және қарапайым процестер сипаттамасының параметрлері.
Өз кезегінде бұл кластардың ішінде модель мен моделдеу объектісіне қатысы мен байланысына қарай параметрлер топтарына бөлінеді.
Конструктивті параметрлер . Бұл класқа моделдеуші объекттің конструктивті құрылымын сипаттайтын геометриялық және құрылымдық параметрлері жатады.
Структуралық (құрылымдық) параметрлерге сандық өрнектері жоқ моделденуші объекттің сипаттаушы характеристикалары тұсіндіреледі. Құрылымдық параметрлер математикалық сипаттаманың түріне біршама әсер етеді.
Геометриялық параметрлерге моделденуші объекттің аппараттық құрылымының сандық характеристикалары түсіндіріледі.
Физикалық параметрлер . Бұл класқа моделденуші объекттің заттар тасқынының физикалық характеристикаларын сипаттайтын параметрлер жатады.
Қарапайым процестер параметрлері. Бұл класқа қарапайым процестердің механизмін сипаттауда қолданылатын гидродинамикалық және физико - химиялық параметрлер жатады.
Алынған моделдеу нәтижесінің дәлдігі математикалық моделдеуге нақты объектінің әртүрлі параметрлері қаншалықты толық көрсетілуіне байланысты. Бірақ моделдегі көрсетілген параметрлердің толықтығы моделдеу сапасын көрсете алмайды.
Математикалық модель біздің уақытымызда кең тараған. Математикалық моделдің дамуына ЭЕМ - ның пайда болуы игі әсерін тигізді, ал әдістің өзі 1000 -жыл бұрын математикамен бірге дүниеге келген еді.
Математикалық моделдеу кейде компьютерсіз де қарастырылады. Математикалық моделдеу шаманы аналитикалық жолмен зерттеуге ұмтылады. Ол сандық шешімнен гөрі ыңғайлы, бірақ кейде математикалық есептерді аналитикалық жолмен шешу мүмкін емес. Мұнда жаңа технологиялық және программалық жабдықталған компьютерде зерттейтін модельдер мен модельдеу қарастырылады. Сондай ақ, модельдеу нәтижелерін көрнекі әрі ыңғайлы түрде көрсету ерекшеленеді. Мысалы: графиктер, таблицалар, динамикадағы иллюстрациялар, дыбыстар мен т. с. с. Бұл кезде компьютер маңызды техникалық құрал болып табылады. Компьютерлік математикалық модельдеуге модельмен жүргізілетін сандық эксперименттер қосылады.
Негізгі этаптары:
- Түсіну. Нақты объекті жан жақты зерттеу, оның структурасын, негізгі қасиеттерін, даму заңдылықтарын және қоршаған ортамен қарым қатынасын толық анықтап білу;
- Басқару. Модель объекті (немесе процесті) басқаруды және берілген мақсаттар мен берілгендер бойынша ең жақсы басқару әдісін анықтауды үйрену үшін керек;
- Болжау. Модель берілген әдістерді жүзеге асырудың тура және жанама салдарын және объектке әсер ету формасын болжау үшін керек. [21]
1-суретте компьютерлік математикалық моделдеу процесінің жалпы схемасы көрсетілген
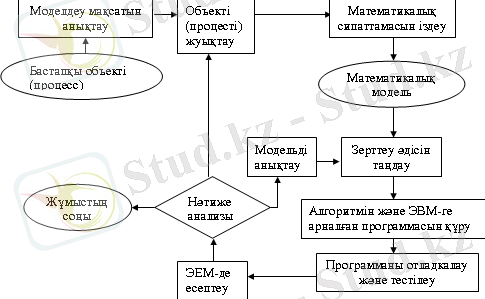 1- сурет
Компьютерлік математикалық модельдеу процесінің жалпы блок схемасы.
1- сурет
Компьютерлік математикалық модельдеу процесінің жалпы блок схемасы.
II ЖАНАРМАЙ СИАНЦИЯСЫНЫҢ ӨНІМДІЛІГІ БІРДЕЙ ЕКІ СТАНЦИЯ ҚЫЗМЕТІНІҢ МОДЕЛІ.
2. 1 Модельденетін объекттің сипаттамасы
Жанармай станциясы кездейсоқ уақытта келетін автомобильдерге қызмет көрсетеді. Егер оларға май құйып берілмесе, онда машиналар кезекке тұрады. Кезектің ұзындығына шектеу жоқ. Автомобильдердің келу арасындағы уақыт параметрі λ Пуассон процессі екені белгілі. Қызмет көрсету уақытының үлестіруі экспоненциялды, тығыздығы f 2 (t) = μexp(-μt), t>=0.
Сұраныстар көзі Кезектер Құрылғылар
Сурет 2. Көпшілікке қызмет көрсету жүйесінің құрылымы
Клиенттердің келу сәттері параметрі λ Пуассон заңын қанағаттандырады дейміз, егер
- кейбір кішкенеdtинтервал уақытында клиентің келу ықтималдығыλdtболса;
- осы уақытта бірден көп клиент келу ықтималдығы өте аз болса;
- келу ықтималдығы бақылау сәтіне және алдында келген клиент уақиғадан бұрынғы өткен жайтқа тәуелді болмаса.
Реквизиция
келу Қызмет көрсету Жіберу
Сурет 3. Кезек күтетін кызмет көрсету кұрылғысы
Осы қасиеттер қарапайым түрде келу тізбегінің үлестіру функциясын анықтауға жеткілікті.
F(t) =1-exp(-λt)
Клиенттер келу интервалының орта шамасы мына формуламен анықталады
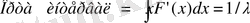 .
.
Көңіл аударатын қасиеттер: егер процестер параметрі λ i тәелсіз пуассондық келу процестерінің суперпозициясы болса, онда ол да пуассондық параметрі λ=Σλ i .
Клиенттер сұрайтын қызмет көрсету уақыты тәуелсіз кездейсоқ айнымалылар болса бәрі бірдей мынандай үлестіру функциясымен анықталатын:
B(t) =P(ts≤t) .
Үлестіру функциясының көңіл аударатын сипаттамалары: қызмет көрсету орта уақыты
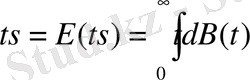
және дисперсиясы
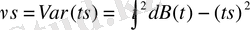
Қызмет көрсету уақыты үлестіруі ретінде жиі қолданыс тапқан экспоненциалды заңы мына функциямен анықталады:
B(t) =1-exp(μt)
Бұл жағдайда орта шамасы және дисперсиясы мыналар болады:
ts=1/μ, νs=1/μ 2
Экспоненциалды үлестіру “зердесінің жоқтығымен” сипатталады: егер клиент қызмет көрсету кезінде “байқалса”, онда қызмет көрсетуге қалған уақыттың үлестіруі қаған қызмет көрсету уақытына тәулді емес. Қызмет көрсету t мен t+dt аралығында аяқталу ықтималдығы нақты μt уақытына тең, уақиғадан бұрынғы өткен жайтқа тәуелсіз.
Сипатталған модельдің негізгі нәтижелері:
ρ=(қызмет көсету орта уақыт) /(орта интервал) =λts
Бұл параметр жүйенің жұмыс бастылығын сипаттайды. Егер ρ>1 , онда орта шамамен ол орындай алатын жұмыстан артық істейді, сол себепті кезек ұзындығы шексіз өседі. Бұл жағдайды шамадан артық жүйе жұмысы дейді. Біз тек қана ρ<1 жағдайын қарастырамыз, яғни стационарлық процесс қалыптасу жағдайын, Басқаша айтқанда жүйенің анықталатын парметрлері уақытқа тәуелді емес жағдайд мына шамаларды табуға болады:
- қызмет көрсету ықтималдығын;
- клиенттердің кезекті күту орта уақытын;
- кезектің орташа ұзындығын (клиенттер санын) .
Қызмет көрсетудің кез келген әдісінде стацинарлы режимде Литтл формуласы бойынша:
N=λW
Бұдан басқа, белгілі
W=Wq+ts
клиенттің жүйеде болу уақыты оның кезекте тұрған уақыты мен қызмет көрсетілген уақытының қосындысы болады. Бұдан
N=Nq+p.
Сонымен ρ қызмет көсету құрылғысының бос тұрмаған нормасы ретінде қарауға болады, ал құрылғы бос тұрғаны, кезек жоқтығы 1- ρ сипатталады.
Берілген уақыт аралығындағы клиентердің түсуі мүмкіндігін математикалық формуламен көрсетуге болады:
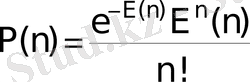
бұл жерде P (n) - берілген уақыт аралығындағы n клиентің түсу ықтималдылығы, E(n) - берілген уақыт аралығындағы n клиентер санының орташа мәні.
Пайдалану коэффиценті 70% қанағаттанарлық жұмыс істейтін жүйені жобалауға болады, бірақ 90% жоғары коэффицент қызмет көрсету сапасын төмендетеді. Егер каналдың жүктелуі 20% болса, онда кезектің пайда болуы екіталай, . ал егер жүктеу 90% құраса, онда, әдетте, кезек пайда болады және өте үлкен болады.
2. 2 Есептің қойылымы
Жанармай станциясында n=2 қызмет көрсететін құрылғы бар. Клиенттер ағыны ықтымалдығының тызыздығы f 2 (t) = μexp(-μt) экспоненциалды үлестіру заңымен берілген. Клиенттер ағыны екі категорияға бөлінеді. Бензин жанармайын құятын клиенттер ағынының ықтималдығының тығыздығы f(t) гамма үлестіру заңымен берілген. Дизель жанармайын құятын клиенттер ағынының ықтымалдығының тызыздығы g(t) экспоненциалды үлестіру заңымен берілген. Клиентке қызмет көрсету уақыты - ықтималдық тығыздығы h(t) бір қалыпты үлестірілген кездейсоқ шама.
Клиентке қызмет көрсету уақыты - ықтималдық тығыздығы h(t) бір қалыпты үлестірілген кездейсоқ шама. Жанармай станциясында кезек күту ұзындығы шектеу жоқ. Кезек күту уақыты ықтымалдығының тығыздығы k(t) нормалды үлестірілген кездейсоқ шама. Кезекке қойылатын шетеулер m [5, 7] интервал шегінен таңдалады.
Клиенттерге бір құрылғыдан көбірек құрылғылардың қызмет көрсету жағдайын қарастырайық, параллелді қызмет көрсету жағдайына тап боламыз. Егерде оның тек “өз” құрылғысы болса, онда бір құрылғымен қызмет көрсету жағдайына тап болар едік, ол 4-і суретте көрсетілген. Белгіленген құрылғымен қызмет көрсету моделі клиенттердің кезекте тұру жалпы уақыты, бірінші босаған құрылғымен қызмет көрсетуден көбірек болады. Модельде қолданылатын көп мастермен қызмет көрсету жүйесі жоғарыда аталған шарттарға негізделеді (қызмет уақыты бір қалыпты үлестірілген кездейсоқ шама) .
Жеке кезек
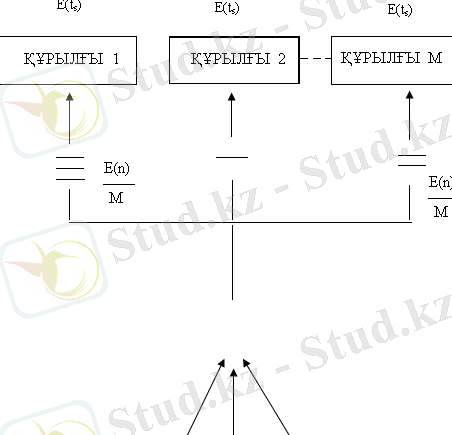
4-ші сурет. Параллелді қызмет көрсетілетін құралдардың М кезектері бар ҚКЖ.
Приоритет бойынша бір ресурсты (процессорды) бөлісу моделін қарастырайық. Реквизиция процессорға басқа тапсырма беруге мүнкіндік береді, таңдалған процесс аяқталмай тұрып. Сондықтан, ол жаңа түскен жұмыстың приоритетін және таңдалған процестің қолданған уақытын ескеруге мүмкіндік береді.
Приоритет бірнеше әдіспен анықталады: бірінші келді - бірінші қызмет көрсетілді (First In, First Out немесе FIFO), “келесі - үлкен жауап қайтару қатынасымен” (Highest Response Next немесе HRN) т. б.
Модельдеу нәтижесінде табу керек:
- автомобильдер кезегінің орташа ұзындығын;
- автомобильдердің кезек күту уақытының орта шамасын;
- автомобильдің жанармай станциясында тұрған орта уақыт;
- жанармай станциясы жабдықтарының бос тұрған орташа уақытын;
- жанармай станциясында тұрған автомобильдер орташа санын.
Жанармай станциясында бірінші келді - бірінші қызмет көрсетілді (First In, First Out немесе FIFO) ” әдісін қарастырамыз. FIFO әдісі приоритетсіз және реквизициясыз бір кезекті пайдаланады. Таңдалған процесс аяқталғанша орындалады, оған ең жақын тұрған процесс кезектің басында болады. Жаңадан келген процесс кезектің аяғына орналасады. Бұл жерде M/G/1 моделі нәтижелерін қолдануға болады. Хинчин-Полачек формуласы жауап қайтару орташа уақытын мына түрде береді :
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz