Математикалық өрнектермен таныстыру

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

Жаркент гуманитарлық-техникалық
колледжінің 401-топ студенті
... ... ... ... ... ... ...
Бастауыш сыныптағы математикалық
өрнектермен жұмыс әдістемесін
оқып үйрену тақырыбы бойынша
жазған курстық жұмысына

Пікір

Бұл курстық жұмыста бастауыш сынып математикасындағы алгебра ұғымы - математикалық өрнек және оны оқыту әдістемесі туралы жазылған. Білім алушы бастауыш сыныпта оқушыларға алгебралық материалдарды жетік меңгерте алғанда ғана, олардың математикадан бiлiм деңгейiнің жоғарылайтынын және тағы басқа пәндердi оқушылардың жетік түсiнетінін, қазіргі заман талабына сай терең білім алуына ықпал жасайтынын тұжырымдай алған.
Студент өз тақырыбында қазіргі жаңа буын математика оқулықтарындағы өрнектерді оқытудың орны мен ролін атап көрсеткен. Бұл курстық жұмыс екі тараудан тұрады. Ол тарауларда бастауыш сынып математикасындағы алгебра элементтері туралы жалпы түсінік, математикалық өрнек ұғымы жайында, сандық өрнектерді оқу, жазу, салыстыру және өрнек құруға үйретуде оқу есептерінің қолданылуы, өрнекпен таныстыру әдістемесі, амалдар тәртібінің ережелерін оқып үйрену, өрнектерді түрлендірумен таныстыру, әріпті өрнек туралы баяндалған.
Студент диплом жұмысын жазу процесі кезінде материалды зерттеу талдау және жүйелеу әдістерін, безендіру тәсілдерін дұрыс пайдаланған, студент тапсырма бойынша барлық қойылған талаптарды толық орындаған.
Жұмыс материалдары ғылыми жүйелі түрде баяндалған, мазмұны түсінікті әрі тілге жатық.
Курстық жұмыстың танымдық маңызы бар, мамандық бойынша арнайы пәндер мен қосымша материалдарға және мерзімді басылымдарға зерттеулер жүргізіліп талданған.Қорытынды нәтижесі жасалынып, негізгі тұжырымдар келтірілген
Комиссия мүшелерінің шешімі бойынша деп бағаланды.

Математиканың теориялық негіздері және математиканы оқыту әдістемесі пәнінің оқытушысы Г.Н.Әшімбекова

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3

1 Тарау. Математиканың бастауыш курсында қарастырылатын алгебра элементтері
Бастауыш сынып математикасындағы алгебра элементтері
туралы түсінік ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

ІІ Тарау Бастауыш сынып математикасында өрнектерді оқыту әдістемесі
2.1 Математикалық өрнектер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
2.2 Амалдар тәртібінің ережелерін оқып үйрену ... ... ... ... ... ... ... ... ... ..
2.3 Әріпті өрнек ... ... ... ... ... ... ... ... ... ... ... ... .
2.4 Педагогикалық іс-тәжірибе нәтижесі. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Қорытынды. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Әдебиеттер. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

КІРІСПЕ

Тақырыптың өзектілігі. Қазіргі заманның талаптарына сай еңбекке, қоршаған ортаға, қоғамға деген қарым - қатынастылықтар мен көзқарастарды қалыптастыру мектеп курсының барлық пәндерін оқыту процесінде жүргізіледі, орындалады. Алайда, осы бағытта математика пәнін алып қарастыратын болсақ, оны оқытудағы әдіс - тәсілдер өте қуатты құрал болып табылатыны сөзсіз.
Математиканың әр қадамы өмірдің қажетінен туады, сабақта
қарастыратын көп есептер адамның практикалық дүниесіне байланысты. Сондықтан математикалық ұғымдардың нақты және тиімді болуы оқушылардың жеке тәрбиесіне байланысты, оқу жүйесіне қойылатын бірінші шарт - ол оқушылардың оқу процесі өмірімен байланысты болуы. Математикадан алған білім, біліктерін оқушылар тек еңбек және оқу әрекеттерінде қолданып қоймай, сонымен қатар мәдениеттің басқа салаларында меңгертуге де пайдалануға болады. Математиканың тәрбиелік әсер етуі - оқушылардың бойында ой - өрісті, саналы ойлай білу ерекшеліктерін, өмірге деген көзқарастарын, танымдық ерекшеліктерін, патриоттық сезімдерін оята отырып дамыту, қалыптастыруда үлкен роль атқарады. Ал, ондай жетістіктерге бастауыш сынып оқушыларына математика сабақтарында математикалық өрнектерді оқытуды ұйымдастыру арқылы жеткізу мүмкін.Оқушыларды санды өрнекпен, әріпті өрнектермен таныстыру, әріптің мәнін өрнектегі орнына қоя білуге баулу, өрнектің мәнін таба білуге үйрету, өрнектерді мәндері бойынша салыстыра білуге дағдыландыру-тақырыптың өзектілігі болып табылады.
Курстық жұмыстың: Оқушылардың математикалық ойлануын дамыту, математикалық мәдениетке тәрбиелеу; оқушылардың математикаға деген ықыласының тиянақты болуын қамтамасыз ету.
Зерттеу объектісі: Бастауыш сыныптың математика сабақтарындағы оқыту процесі.
Курстық жұмыстың: Егер бастауыш сыныпта оқушыларға алгебралық материалдарды, соның ішінде өрнетерді жетік меңгерте алсақ, онда олардың математикадан бiлiм деңгейi жоғарылайды, қазіргі заман талабына сай терең білім алуына ықпал жасайды.
Курстық жұмыстың міндеттері:
-Бастауыш сыныптың математика сабағында алгебра элементтерін оқыту арқылы оқушылардың ой - өрiсiн дамыту мүмкiндiктерiн анықтау;
-Өрнектің мәнін табу тәсілдерін қарастыратын ретпен оқытып үйрету және олардың көмегімен есеп шығаруды қарастыру. Курстық жұмыстың практикалық құндылығыБастауыш сыныпта математиканы оқыту әдістемесін жетілдіруде, студенттердің iс - тәжiрiбесiнде қолдануға болады.
Зерттеу жұмысы кіріспе бөлімнен, негізгі бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен тұрады.

1 Тарау. Математиканың бастауыш курсында қарастырылатын алгебра элементтері
Бастауыш сынып математикасындағы алгебра элементтері туралы түсінік

Математика бастауыш курсының өзекті мәселесі теріс емес бүтін сандар, олармен жүргізілетін амалдар, шамалар және оларды өлшеу болып табылады. Осы өзектің төңірегінде алгебра және геометрия элементтері шоғырландырылған. 1969 жылғы бағдарламаға сәйкес математиканың бастауыш курсында алгебра әлементтері енгізіледі, осыған байланысты Алгебра элементтері тақырыбында, атап айтқанда өрнек, теңдеу, теңсіздік, теңдеулер жүйесі, теңсіздіктер жүйесі мен жиынтығы және т.б. ұғымдарды қарастыру барысында жалпы ұғымдар мен әр алуан жиындар туралы білімдер кеңінен қолданылады.
Бастауыш сынып оқушылары математикалық өрнектермен танысып қана қоймай, санды теңдіктер мен теңсіздіктер жайлы мағлұматтар алса, әріптік символика және айнымалысы бар өрнектер, қарапайым теңдеулер мен теңсіздіктерді шешуге үйренсе,теңдеулер құру арқылы шығарылатын жай және құрама есептердің түрлерімен танысса, оқушылардың білімдерінің терендей түсетіні сөзсіз. Практикалық іс-тәжірибе көрсеткендей бұл жұмыстар озық тәжірибелерді жинақтай түсу, әдістемеліктерді жетілдіру мәселелеріне әрқашан ерекше көңіл бөлуі тиіс, ал бұл алгебралық материалдарды оқытуда мәні зор.
Алгебралық материал 1-ші сыныптан бастап арифметикалық, шама және геометриялық материалдармен тығыз байланыста оқылады.
Мұнда оқушылар алгебра элементтері математикалық өрнектер, сандық теңдіктер мен теңсіздіктер жайлы алғашкы мағлұматтар алуы тиіс, айнымалысы бар өрнекпен танысуы керек, қиын емес теңдеулер мен теңсіздіктерді шешуді үйрену, теңдеулер құруда жай және күрделі есептерді шығару дағдысын игерулері керек және санды теңдік, санды теңсіздік, санды өрнек, әріпті өрнек, теңдеу сияқты ұғымдардың мәнді белгілерін еске түсіру және оларды бір-бірінен ажыратуға машықтандырудың қажеттігі ескерілуі тиіс, себебі, ілгеріде осы ұгымдарымен байланысты мәселелер жиірек қарастырыла бастайды және біртіндеп күрделене түседі. Сондықтан өрнекті кұру, оқу, жазу, оның мәнін табу, оларды бір-бірімен салыстыру, қарапайым теңдеулері сияқты мәселелерді пысықытауға мән беріледі.Алгебра элементтерін енгізу, сан және арифметикалық амалдар, математикалық катынастар туралы ұғымдарды жалпылауға көмектеседі.
Негізгі алгебралық ұғымдарға курста санды теңсіздік және теңдік, өрнек, сандық өрнектің мәні, әріпті өрнек, әріпті өрнектің мәні, әріптің әрбір мәніне өрнектің бір ғана мәнінің сәйкес болатындығы, қарапайым теңдеулер және оларды шешу тәсілдері, алгебралық тәсілмен есептер шығару және тағы басқалар жатады.

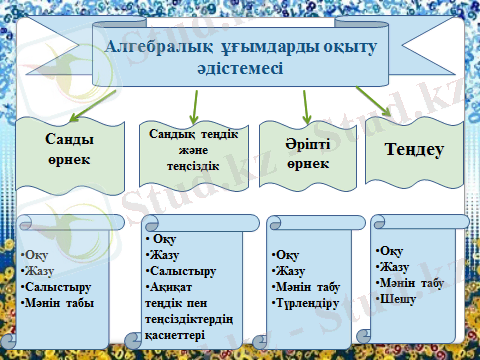
Бұл ұғымдарға бастауыш сыныптарда анықтама берілмейді, олар көрнекілік, жаттығулар арқылы қалыптастырылады.
Тақырыпты оқытып үйретудің міндеттері:
Теңдік, теңсіздік ұғымымен таныстыру;
Өрнектерді оқи, жаза және салыстыра білу біліктерін қалыптастыру;
Санды өрнектермен жүргізілетін жұмыстардың табиғи жалғасы ретінде қарапайым әріпті өрнектерді бір - бірімен ажырату, оларды оқу, жазу және құру, әріпті өрнектің берілген мәнінде мәнін табу жайында түсінік қалыптастыру, тәжірибе жинақтау.
Алгебра элементтерінің ішінде дидактикалық тұрғыдан алғанда аса маңыздысы - теңдеу жайында түсінік беру және оны шешудің тәсілдерін оқытып - үйрету.
Жақша, амал ретімен оқытып үйрету.
Есепті алгебралық тәсілмен шешудің мән мағынасын ашу. Теңдеулер құруға келтірілетін арифметикалық есептер шығару.Арифметикалық амалдардың белгісіз компоненттерін табу, теңдеудің жәрдемімен шығару.Арифметикалық амалдың компоненті немесе нәтижесінің санды өрнек түрінде болып келуі мүмкін теңдеулер құрылатын есептер ұсынылады.Мұнда құрама есепті теңдеу жәрдемімен шығару көрсетіледі.Теңдеулер құру арқылы шығарылатын құрама есептер қарастырылады. Оларды шығару барысында алгебралық тәсілді енгізу және оның мәнді ерекшелігі мен артықшылығын нақты көрсетіп беру қажет.
Теңдеулерді шешу тәсілдерін қарастыратын ретпен оқытып үйрету және олардың көмегімен есеп шығаруды қарастыру бастауыш буын оқушыларын келесі сыныптардың талабына сай дайындауды қамтамасыз етеді. Өйткені, олар теңдеуді шешуге дағдыланады және теңдеу құру арқылы есеп шығарудың тәсілінің мән - мағынасы, ерекшелігі жайында бастама түсінік алды. Соның нәтижесінде алгебра элементтерін оқытудың басты мақсатына жетудің негізі қаланады.

Төртінші сыныптағы математикалық білімінің мазмұнында 1-3 сыныпта өтілген алгебра элементтерінің мазмұндық-әдістемелік желілері әрі қарай сабақтастыра жалғастырылады. Осы бағыт бойынша бастауыш буынының соңғы 4-сыныбында қайталау мен пысықтау және қорытындылау оңтайлы үйлестіріледі.Алгебраның элементтері болып табылатын санды теңдік, санды теңсіздік, санды өрнек, әріпті өрнек, теңдеу сияқты ұғымдардың мәнді белгілерін еске түсіру және оларды бір-бірінен ажыратуға машықтандырудың қажеттігі ескерілуі тиіс. Себебі, ілгеріде осы ұғымдармен байланысты мәселелер жиірек қарастырыла бастайды және біртіндеп күрделене түседі. Сондықтан өрнекті құру, оқу, жазу, оның мәнін табу, оларды бір-бірімен салыстыру, қарапайым теңдеулері сияқты мәселелерді пысықытауға мән беріледі. Сондай-ақ, өрнектермен байланысты жұмыстарды орындау барысында амалдардың орындалуының рет-тәртібі жайындағы ережелерді қолдануға машықтандыру түсу көзделеді. Осы ережелер өрнекті құру және оны оқу кезінде екі бағытта қолданылатынын ескеру керек. Өрнекті құру кезінде ең алдымен бірінші орындалатын амалмен байланысты өрнек жазылады, содан кейін екінші амалмен жазылатын өрнек, т.с.с. әрі қарай осылайша жалғаса береді. Ал өрнекті оқу кезінде, ең алдымен соңғы орындалатын амал, яғни өрнек қосынды, айырма, көбейтінді, бөлінді екені анықталады, сонан соң сәйкес амалды анықтайтын сандар немесе өрнектер сараланады. Демек, осы екі бағытта іс-әрекет жасауға балаларды машықтандырған жөн.
Өрнектермен жұмыс дүркін-дүркін қайталанып отырады. Дегенмен осы ұғыммен байланысты мәселелерді біршама қорытындылап және оны жаңа жағдайда қолдануға ерекше көңіл бөлінеді, өйткені ілгеріде екі амалмен шығарылатын есепті теңдеу құру арқылы шешудің мән-мағынасы ашылады, сонда өрнектер жайындағы оқушылардың игерген білімі тірек болуы тиіс. Шындығында есеп мазмұны бойынша теңдеу құру, алдымен оның құрамына енетін өрнектерді құрумен байланысты, әрі қарай сол құрылған өрнектерден теңестірілетіндері сараланады. Демек, өрнек құруды, оқуды, жазуды және оның мәнін табуды, оларды салыстыруды игере алмаған оқушы есепті теңдеу құру арқылы шығару тәсілін де меңгере алмайды.
Сондықтан пысықтау кезінде мына сияқты мәселелерге көңіл бөлінеді:
-басқа жазулардың ішінен өрнектерді ажырата білу;
-өрнектерді мәнді белгісіне қарай топтарға (санды және әріпті өрнекерге) бөлу; санды өрнектерді құру және оқу;
-санды өрнектің мәнін табу;
-әріпті өрнек құру және оқу, санды өрнектің мәнін табу және оларды салыстыру;
-бірнеше амал араласып келетін және амалдардың орындалу реті ережесін қолдануға тәуелді болатын санды өрнектердің мәндерін есептеу.
Ал ілгеріде есепті тендеу құру арқылы шығарғанда есеп мазмұнына орай құрылатын тендеудің құрылысы оқушылар шеше алатын, яғни түбірін таба алатын теңдеулердің құрылысындай болу тиіс. Алайда бір есептің өзі бойынша жүргізілетін талқылауға байланысты әр түрлі тендеулер құрылуы мүмкін. Осындай жағдайда оқушыларға әріпті өрнек болып келетін тендеулерді шешу тәсілімен оқушыларды біртіндеп таныстыруды жүзеге асыру артық болмайды.
Амал компоненттерінің бірі санды өрнек болып келетін теңдеуді шешудің оқушыларға белгілі тәсілдеріне ұқсас болғанмен, біршама күрделі болып келеді және теңдеуді шешу процесінің қадамдары арта түседі.
Әріпті өрнектерді құру және оларды оқу мен жазу теңдеу құру арқылы шығаруға дайындық болып табылады, өйткені есеп мазмұнына қарай құрылатын теңдеу әрдайым санды және әріпті өрнектерді құрумен байланысты болады да, ол өрнектер тендеудің құрамына енеді. Теңдеу құру арқылы әр түрлі тақырыпқа байланысты және құрылысы да бір-бірінен өзгеше есептерді шығару ұсынылады.
Теңдеулер және оларды шешу тәсілдерін қарастырумен байланысты жұмыс ұғымдар мен терминдердің болатыны жайында мағлұмат беру, қарапайым және құрылысы біршама күрделі теңдеулерді әр түрлі білімге сүйеніп құру және шешу сияқты мәселелердің төңірегінде өрбиді. Бұл да келесі сыныптарда математиканы оқып үйрену үшін өте қажетті дайындық болып табылады.

ІІ Тарау Бастауыш сынып математикасында өрнектерді
оқыту әдістемесі
2.1 Математикалық өрнектер

Математикалық өрнектермен таныстыру.
Мақсаты: оқушыларға алгебра элементтерін оқыту.
Міндеттері:
1. Сандар мен өрнектерді салыстыру негізінде санды теңдік жэне теңсіздік ұғымдарымен таныстыру.
2. Өрнектерді оқуға, жазуға, өрнектердің мәнін табуға, салыстыруға үйрету.
3. Қарапайым өрнектермен (сандардың қосындысы, айырмасы, көбейтіндісі, бөліндісі) және олардың мәндерімен, сондай-ақ амалдардың компоненттерімен таныстыру.
4. Санды және әріпті өрнектер жэне олардың мэндерін табуға үйрету.
Математика бағдарламасы бойынша 1-4 сыныптарда балаларды математикалық өрнектерді оқуға және жазуға үйрету, амалдарды орындау тәртібімен таныстыру және есептеулерде оларды пайдалануға үйрету, оқушыларды өрнектерді теңбе-тең түрлендірумен таныстыру жағы қарастырылады.

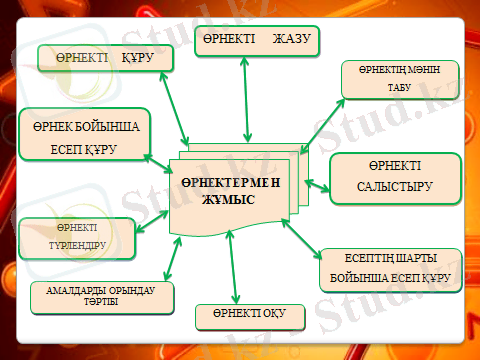
Өрнектермен жұмыс мақсаты:

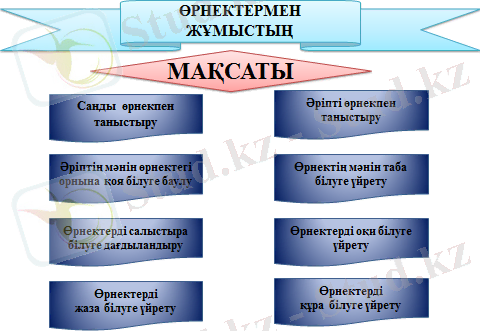
Өрнектерді оқуға, жазуға, өрнектердің мәнін табуға, салыстыруға үйрету,
өрнек ұғымымен оқушы бірінші сыныпта танысады.
2+1
1+2
3-1
3-2 - бұлар өрнектер
Өрнектер - бұл цифрлар мен таңбалардың көмегімен орындалған жазу екендігі түсіндіріледі.
Өрнекте көрсетілген амалдарды орындау арқылы өрнектің мәнін табуға болады.
2+1=3
3 - өрнектің мәні
Өрнектің мәні амалдарды орындауда табылатын нәтиже.
Қарапайым өрнектермен (сандардың қосындысы, айырмасы, көбейтіндісі, бөліндісі) және олардың мәндерімен, сондай-ақ амалдардың компоненттерімен таныстыру.
Оқушылар қосынды - +, айырма -- - таңбасы қолданылатын қарапайым өрнектің атауларымен танысады. Сондай-ақ амалдар компоненттерімен танысады: бірінші қосылғыш, екінші қосылғыш, азайғыш, азайтқыш. Қосындының мәнін және айрыманың мәнін таба білуді үйренеді.Қосу мен азайтудың өзара байланысын тағайындайды.
Көбейтінді ::, бөлінді : таңбасы қолданылатын қарапайым өрнектер атауларымен танысады. Көбейтудың мәні, бөлудің мәні, осы амалдар компоненттері енгізіледі. Көбейту мен бөлудің өзара байланысы белгіненеді.
Санды және әріпті өрнектер және олардың мәндерін табуға үйрету.
6+4
10-7 - бұлар санды өрнектер.
Балаларда математикалық өрнек жайлы түсінігін қалыптастырғанда сандар арасында қойылған амал таңбасының екі түрлі мағынасы бар екендігін ескеру қажет: ол бір жағынан сандар қолданылатын амалды білдіреді (мысалы, 6+4 алтыға төртті қосу); екінші жағынан амал таңбасы өрнекті белгілеу қызметін атқарады (6+4 6 мен 4 сандарының қосындысы).
Өрнектермен жұмыс әдістемесінде екі кезең қарастырылған. Олардың біріншісінде қарапайым өрнектер (екі санның қосындысы, айырмасы, көбейтіндісі, бөліндісі) туралы ұғым, ал екіншісінде күрделі өрнектер
( көбейтінді мен санның қосындысы, екі бөліндінің айырмасы т.б.) туралы ұғым қалыптастырылады.Өрнек, оның түрлері мен өрнектің мәні атты мәселелер бастауыш математика курсында арифметикалық амалдар туралы ұғыммен тығыз байланыста қарастырылады және оларды оқушылардың терең меңгеруіне ықпал жасайды. Жалпы,математика курсында өрнектер - құрамындағы элементтердің жағдайына қарай санды өрнек және әріпті өрнек деп екіге бөлінеді.
Санды өрнек дегеніміз - сандардан, амалдар таңбаларынан және жақшалардан құрылған математикалық сөйлем.
Мысалы 5+3, 7-2, 21:(3+4) т.б.
Жеке санның өзін де санды өрнек десек, өрнектің анықтамасына қайшы келмейді.
Демек, өрнек бір саннан немесе бірнеше саннан, амал таңбаларынан және жақшалардан тұруы мүмкін. Ал егер өрнек бір амалдан тұрса онда мақсат - амалды орындау. Егер өрнекте бірнеше амал болса, онда сол амалды ережелерге сәйкес орындау қажет. Бұл операцияны математикада өрнектің мәнін табу деп атайды. Санды өрнекте өрнектің мәні сан болады. Жалпы, 1-сыныпта өрнектің қосынды және айырма деп аталатын түрі ғана қарастырылады. Демек, қосынды мен айырма, бұл - өрнектер.
Өрнектің мәнін табу үшін өрнектегі қажетті амалды орындау керек.
Бірінші өрнекпен - екі санның қосындысымен таныстыру І сыныпта 10 көлемінде қосу және азайтуды оқығанда болады.
Жиындармен операциялар орындағанда балалар алдымен қосу мен айырманың нақты мағынасын меңгеріп алады, сондықтан 5+1, 6-2 түріндегі жазуда амалдардың таңбаларын олар қосу,азайту сөздерінің қысқаша белгісі ретінде түсінеді.Содан кейін балаларплюс,минусамалдар таңбаларының аттарын білетін болады және амалдар таңбаларын атай отырып, мысалдарды оқиды (4 қосу 2 алтыға тең болады, 7 азайту 2 беске тең болады).
Компоненттердің және қосу амалы нәтижесінің аттарымен таныса отырып, оқушылар қосудың нәтижесі болып табылатын санды белгілеу үшін қосынды деген терминді пайдаланады.
Қосудағы сандардың аттары жөніндегі балалардың біліміне сүйене отырып, мұғалім қосу таңбасымен қосылған екі саннан тұратын қосуға берілген мысалдардың жазуы тең таңбасының екінші жағында тұрған сан сияқты аталады (5-қосынды, 4+1-де қосынды). Көрнекі түрде ол былай кескінделеді:

Осындай жаттығуларды орындау процесінде оқушылар қосынды терминінің екі түрлі мағынасын біртіндеп түсіне бастайды: сандардың қосындысын жазу шін оларды плюс таңбасымен қосу керек; қосындысының мәнін табу үшін берілген сандарды қосу керек.
Мына өрнектермен орындалатын жұмыс та шамамен осындай тұрғыда жүргізіледі: екі санның айырмасы (І сынып), көбейтіндісі және бөліндісі (ІІ сынып). Алайда енді осы терминдердің әрқайсысы амал нәтижесінің аты ретінде де және өрнектің аты ретінде де бірден енгізіледі. Өрнектерді оқу және жазу, олардың мәнін сәйкес амалдардың көмегімен таба білу қосындыға берілген жаттығу сияқты жаттығуларда көп рет орындау процесінде қалыптасады.
10 көлемінде қосу және азайтуды оқығанда үш және одан да артық сандардан тұратын , амалдардың бірдей немесе әр түрлі таңбаларымен қосылған мына түрдегі өрнектер қосылады:
3+1+1, 4 -1 -1, 2+2+2+2, 7 - 4+2, 6+3 - 7.
Осындай өрнектердің мағынасын айқындай отырып, мұғалім оларды қалай оқитындығын көрсетеді ( мысалы, үшке бірді қосу керек және алынған санға тағы бірді қосу керек ). Бұл өрнектердің мәндерін есептеп шығара отырып, оларға тұжырымдама жасамаса да, балалар іс жүзінде жақшасыз берілген өрнектерге амалдар қолдану тәртібін игереді.
Бұдан біраз кейін балаларды өрнектерді есептеп шығару процесінде оларды түрлендіруге үйретеді, мысалы: 10-7+5=3+5=8.
Мұндай жазулар теңбе-тең түрлендіруге жасалған алғашқы адым болып табылады.
Екінші сынып оқушыларын 10-(6+2), (7-4)+5 т.б. түріндегі өрнектермен таныстыру оларды санды қосындыға қосу, санды қосындыдан шегеру т.б., құрама есептердің шешуін жазу ережесін үйренуге дайындайды, сондай-ақ өрнек ұғымын тареңірек меңгеруге көмектеседі.
Оқушыларды 10+(6-2), (5+3) - 1 түріндегі өрнектермен таныстыру әдістемесі әр түрлі болады. Оқушыларды үлгісіне қарай отырып, ұқсастық бойынша дайын өрнектерді оқуға және амалдар тәртібін түсіндіре отырып, өрнектердің мәндерін есептеп шығаруды бірден үйретуге болады. Нақты мысалдарды қарастыра отырып, мұнда сандардың қосындысын (айырмасын) қосатынын, не азайтатынын, сондықтан қосындыны (айырманы) жақша ішіне алып, әуелі қосынды (айырма) неге тең екенін есептеп шығарылады, содан кейін ғана осы шыққан санға амал қолданатынын балаларға көрсету керек.Алдағы уақытта түрлі жаттығулар процесі кезінде оқушылар осындай өрнектердің мәндерін оқи, жаза және таба білуді біртіндеп игеретін болады.Мысалы өрнекті оқуға,жазуға,құруға және мәнін табуға байланысты математикалық диктант алуға болады,әртүрлі ойындар ойнатуға болады.

Ойын Әр машинаның гаражын тап
Машинаға жазылған өрнектердің мәндеріне сәйкес келетін гаражды тауып, әр машинаны өз гаражына кіргізуге көмектесіңдер.
92
13
70
24
59
67
93
14
10+60-3
60-40+4
30+30-1
97-7+2
100-10+3
9+1+60
10+5+-1
65+3-1
92
13
70
24
59
67
93
14
10+60-3
60-40+4
30+30-1
97-7+2
100-10+3
9+1+60
10+5+-1
65+3-1

Өрнектерді құру және олардың мәндерін таба білуді оқушылар құрама есептерді шығарғанда падаланады, есептердің шешулерінің жазуындағы өрнектердің нақты мағынасын түсінеді. Бұл тұрғыдан алғанда мынадай жаттығу пайдалы: есептің шарты беріледі,
мысалы: Баланың 90 теңгесі бар еді, балмұздақ 42 теңге, ал кәмпит 36 теңге тұрады. балалар бұл жағдайда мына өрнектер нені білдіретінін түсіндіреді:
90-42 42+36 90-36 90-(42+36)
ІІ сыныпта бұрын қарастырылған өрнектермен қатар екі жай өрнектерден тұратын өрнектер, мысалы: (50+20)+(30+10). Сондай-ақ сан мен көбейтіндіден немесе екі санның бөліндісінен тұратын өрнектер енгізіледі, мысалы: 7·3-5, 27:9+17. Амалдарды орындау тәртібі олардың жазумен сәйкес келмейтін жерде жақша пайдаланылады: 16+(8:4), 50-(3·9). І кластағы сияқты, балалар осындай өрнектерді оқуға және жазуға жаттығады, есептеулерді түсіндіре отырып, олардың мәндерін табады.
ІІ сыныпта математикалық өрнек және математикалық өрнектің мәні терминдері енгізіледі (анықтамасыз). Бірнеше мысалды бір амалға жазғаннан кейін мұғалім бұл мысалдар басқаша түрінде математикалық өрнектер деп аталатындығын хабарлайды. Мұғалімнің тапсырмасы бойынша балалардың өздері түрлі өрнектер құрастырады.

Мұғалім нәтижені есептеп шығаруды ұсынады және нәтиже дегеніміз басқаша математикалық өрнектердің мәндері деп аталатындығын түсіндіреді.
Күрделі өрнектерде қарапайым өрнектерді қосатын амалдар таңбаларының да екі жақты мағынасы бар, оны оқушылар біртіндеп айқындай түседі. Мысалы, 20+(34-8) өрнектерде + таңбасы 20 саны мен 34 және 8 сандарының айырмасына қолданатын амалды білдіреді.Сонымен қатар + таңбасын қосындыны белгілеу үшін қолданылады, бұл өрнек - бірінші қосылғышы 20-ға тең, ал екінші қосылғышы 34 пен 8 сандарының айырмасы арқылы өрнектелген қосынды.
Балалар күрделі өрнектердегі амалдарды орындау тәртібімен танысқаннан кейін жеке компоненттері өрнектермен берілген қосынды, айырма, көбейтінді, бөлінді ұғымдарын қалыптастыруға кіріседі.
Алдағы уақытта өрнектерді оқуға, құруға және жазуға көпрет жаттығу процесінде оқушылар біртіндеп күрделі өрнектің (2-3 амалдан тұратын) түрін тағайындау дағдысын игеретін болады. Бұл жұмысты коллективті түрде құрылатын схема едәуір жеңілдіктерді және мынадай өрнектерді оқығанда пайдаланылады:
қандай амал ең соңымен орындалатынын тағайындау керек;
осы амалды орындағанда сандар қалай аталатынын еске түсіру керек;
бұл сандар қалай өрнектелгенін оқу керек.
Қарапайым өрнектермен берілген амалдар компоненттерінен тұратын күрделі өрнектерді оқу және жазуға жаттығулар жүргізу балалардың амалдар тәртібі ережесін игеруге көмектеседі.
Өрнекті түрлендіру - өрнектің мәні берілген өрнектің мәніне тең болатын берілген өрнекті басқа өрнекпен алмастыру болып табылады. Оқушылар мұндай өрнектерді түрлендіруді арифметикалық амалдардың қасиеттері мен одан шығатын сандарға (қосындыны санға қалай қосу керектігі, санды қосындыдан қалай шегеру керектігі, санды көбейтіндіге болатындағы жайлы т.б. ережелер) сүйене отырып орындайды.
Әр ережені оқып үйренуде оқушылар қандай да бір түрдегі өрнектерде амалдарды түрліше орындауға болатындығына. Бір ақ мұнда өрнектің мәні өзгермейтіндігіне көздерн жеткізеді. Алдағы уақытта оқушылар амалдар қасиеттері туралы білімін берілген өрнектерді олармен тең өрнектерге олармен тең өрнектерге түрлендіру үшін пайдаланапды. Мысал, мына өрнектердің жазуын = таңбасы сақталатындай етіп жалғастыру ұсынылады:
76-(20+4)=76-20...
(10+7) ·5=10·5...
60(2·10)=60·10...
Бірінші тапсырманы орындай отырып оқушылар былай пайымдайды: сол жағынан 76-дан 20 мен 4 сандарының қосындысын шегеру керек, ал оң жағында 76 дан 20-ны шегердік; сол жақта қанша болса, оң жақта да сонша болу үшін оң жағынан тағы 4-ті шегеру керек. Осылайша басқа өрнектерде түрлендіріледі, яғни өрнекті оқып, оқушы сәйкес ережені есіне түсіреді және амалдарды ережені бойынша орындай отырып, түрлендірілген өрнек алады. Түрлендірудің дұрыстығына көз жеткізу үшін балалар берілген және түрлендірілген өрнектердің мәндерін есептеп шығарады және оларды салыстырады.
Есептеу әдістерін негіздеу үшін амалдар қасиеттері туралы білімді қолдана отырып, мына түрдегі өрнектерді түрлендіруді орындайды:
36+20=(30+6)+20=(30+20)+6=56
72:3=(60+12):3=60:3+12:3=24
18·30=18·(10·3)=(18·3) ·10=540
Мұнда сондай-ақ оқушылар әрбір келесі өрнек неге негізделіп алынатынын тек түсіндіріп қана қоймай, сонымен қатар барлық бұл өрнектер = ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.