Транспорттық есептерді модельдеу және шешу: қойылымы, бастапқы жоспарлар мен потенциалдар әдісі


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
АКАДЕМИК Е. А. БӨКЕТОВ АТЫНДАҒЫ ҚАРАҒАНДЫ УНИВЕРСИТЕТІ
МАТЕМАТИКА ЖӘНЕ АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАР ФАКУЛЬТЕТІ
«ҚОЛДАНБАЛЫ МАТЕМАТИКА ЖӘНЕ И НФОРМАТИКА» КАФЕДРАСЫ
КУРСТЫҚ ЖҰМЫС
«Операцияларды зерттеу есептерін модельдеу» пәнінен
«Транспорттық есептер» тақырыбы бойынша
Орындаған: МКМ-19-1 топ ст. Тұрғынбек А. А
Қабылдаған: аға оқытушы Есендаулетова Ж. Т
ҚАРАҒАНДЫ 2022 ЖЫЛ
Мазмұны
Кіріспе . . . 3
§ 1. n айнымалысы үшін транспорттық есептің (ТЕ) қойылымы . . . 4
§2. Теориялық материал . . . 7
2. 1 Транспорттық есептерінің жалпы тұжырымы . . . 7
2. 2 Транспорттық есептің негізгі жоспарын құру әдістері . . . 11
2. 3 Минималды элемент әдісі . . . 12
2. 4 Потенциалдар әдісі . . . 13
§3. Әртүрлі критерийлер бойынша транспорттық есептер . . . 20
§4. Excel бағдарламасында транспорттық есепті шешу . . . 21
§5. Қорытынды . . . 26
§6. Пайдаланылған әдебиеттер . . . 27
Кіріспе
«Транспорттық есеп» деген атпен есептердің кең ауқымы бір математикалық модельмен біріктірілген. Классикалық транспорттық есеп, біртекті өнімді немесе бір-бірін алмастыратын өнімді өндіріс орындарынан тұтыну нүктелеріне тасымалдаудың ең үнемді жоспарының есебі сызықтық бағдарламалаудың практикалық қолдануларында жиі кездеседі. Сызықтық программалау - математикалық бағдарламалаудың бір саласы - шектеулері бар көпөлшемді экстремалды есептерді шешудің теориясы мен сандық әдістерін әзірлейтін математика саласы.
Ықтимал транспорттау нұсқаларының үлкен саны эмпирикалық немесе сараптамалық түрде жеткілікті үнемді жоспарды алуды қиындатады. Тасымалдауды жоспарлауда математикалық әдістер мен есептеу әдістерін қолдану үлкен экономикалық нәтиже береді. Көлік тапсырмаларын симплекс әдісімен шешуге болады, дегенмен транспорттық тапсырманың шектеулер жүйесінің матрицасы ерекше болғандықтан, оны шешу үшін арнайы әдістер әзірленген. Бұл әдістер симплекс әдісі сияқты бастапқы анықтамалық шешімді табуға, содан кейін оны жетілдіре отырып, оңтайлы шешімді алуға мүмкіндік береді.
Транспорттық есептің түрлері
Транспорттық есептің шарттары мен шектеулері өте ауқымды және әртүрлі. Сондықтан оны шешудің арнайы әдістері әзірленді. Олардың кез келгенінің көмегімен сіз анықтамалық шешім таба аласыз. Содан кейін оны жақсартып, ең жақсы нұсқаны алыңыз.
Транспорттық есеп шарттарын екі жолмен көрсетуге болады:
• желілік (схема) түрінде;
• матрицалық (кесте) түрінде.
Шешу процесінде шектеулер болуы мүмкін (немесе есеп оларсыз шешіледі) .
Шарттардың сипаты бойынша көлік міндеттерінің келесі түрлері бөлінеді:
• ашық тасымалдау тапсырмалары (жеткізушінің тауар қоры тұтынушының тауарға сұранысына сәйкес келмейді) ;
• жабық (жеткізушілер мен тұтынушылардың өнімдерінің жалпы қоры бірдей) .
Жабық трансорттық есепті потенциалды әдіспен шешуге болады. Оған әрқашан рұқсат етілген. Ашық түр жалпы қорға жетіспейтін бірліктерді қосу немесе теңдікке жету үшін өнімге қажеттілік арқылы жабық түрге қысқарады.
Транспорттық есептің мақсаты - өнімді (тауарды) тұтынушыға қажетті уақытта және қажетті жерде еңбек, материалдық, қаржылық ресурстардың мүмкін болатын ең аз жалпы құнымен алуын (жеткізуін) қамтамасыз ету.
Транспорттық есептің мақсаты алты шарт орындалғанда қол жеткізілген болып саналады:
- қалаған өнім;
- талап етілетін сапа;
- қажетті мөлшерде жеткізіледі;
- қажетті уақытта;
- дұрыс жерге;
- ең аз шығынмен.
Зерттеу объектісі өндірістік және коммерциялық қызметпен жүретін материалдық және сәйкес қаржылық, ақпараттық ағындар болып табылады.
§1. n айнымалысы үшін транспорттық есептің (ТЕ) қойылымы
Біртекті өнімдердің бірнеше жеткізушілері (әрқайсысының белгілі бір қоры бар) және осы өнімнің бірнеше тұтынушылары (әрқайсысының қажеттіліктері белгілі) болсын. Сондай-ақ әрбір жеткізушіні әрбір тұтынушымен байланыстыратын коммуникациялар желісі (жолдар, өзендер, әуе желілері және т. б. ) берілген. Әрбір байланыс желісінде тасымалдау бағасы - өнім бірлігін тасымалдау құны белгіленеді. Егер байланыс болмаса, онда ол бар деп есептейміз, бірақ біз оған тасымалдау бағасын шексіздікке (+∞) тең етіп белгілейміз. Бұл келісім оның бойымен тасымалдауды тиімсіз етеді және бұл қатынасты тасымалдау жоспарынан автоматты түрде алып тастайды.
Осылайша, жеткізушілерден қорды алып тастау арқылы тұтынушылардың қажеттіліктерін қанағаттандыру үшін өнімді жеткізушілерден тұтынушыларға тасымалдау жоспарын жасау қажет. Мақсат - барлық тасымалдаудың жалпы құнын барынша азайту.
Транспорттық есептердің міндеттері:
1) ашық m ≠ n (жеткізушілерден алынатын өнімдердің жалпы қоры тұтынушылардың өніміне жалпы қажеттілікпен сәйкес келмейді) .
2) жабық m = n (жеткізушілерден қол жетімді өнімдердің жалпы қоры тұтынушылардың өніміне жалпы қажеттілікке сәйкес келеді) .
Потенциалдар әдісі тек жабық ТЕ үшін «жұмыс істейді», сонымен қатар жабық ТЕ әрқашан шешілетін болады.
Ашық ТЕ жабық ТЕ-ке жетіспейтін бірліктерді өнімнің жалпы қорына немесе жалпы өнім қоры мен өнімге қажеттілік тең болғанға дейін өндірістің жалпы қажеттілігіне қосу арқылы азайтылады.
Жабық траспорттық есеп келесі формадағы сызықтық бағдарламалау мәселесі (СБМ) ретінде тұжырымдалған:
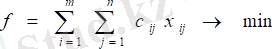 (1)
(1)
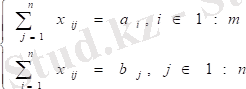 (2)
(2)
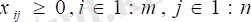
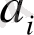 - i-ші жеткізушінің қоры
- i-ші жеткізушінің қоры
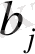 - j-ші тұтынушының қажеттілігі
- j-ші тұтынушының қажеттілігі
 байланысқа арналған өнім бірлігін тасымалдау бағасы (i, j)
байланысқа арналған өнім бірлігін тасымалдау бағасы (i, j)
(i-ші жеткізушіден j-ші тұтынушыға дейін)
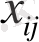 - коммуникациялар бойынша өнімді тасымалдау көлемі (белгісіз) (i, j) .
- коммуникациялар бойынша өнімді тасымалдау көлемі (белгісіз) (i, j) .
Транспорттық есептің оңтайлылығының критерийін алу үшін қосарлы есеп құрастырамыз.
Тасымалдау есебінің шектеу матрицасының құрылымы айнымалыға сәйкес бағанда дәл екі нөлдік емес элемент болатындай: біреуі i саны бар жолда және біреуі m + i жолында.
Қос айнымалылар векторы Y = (
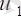 , …,
, …,
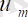 ,
,
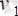 , . . . ,
, . . . ,
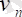 ) m + n құраушыға ие (ТЕ шектеулерінің санына сәйкес), олар потенциалдар деп аталады: айнымалылар
) m + n құраушыға ие (ТЕ шектеулерінің санына сәйкес), олар потенциалдар деп аталады: айнымалылар
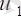 ,
,
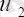 , …,
, …,
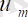 жеткізушілердің потенциалдары; айнымалылар
жеткізушілердің потенциалдары; айнымалылар
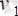 ,
,
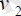 , …,
, …,
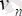 - тұтынушылардың потенциалдары.
- тұтынушылардың потенциалдары.
Стандартты нысанда СБМ-не қосарлы есепті құру схемасын пайдалана отырып, бізде:
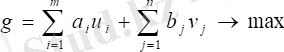 (3)
(3)
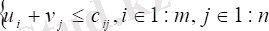
Алынған қосарлы есепте ТЕ-нің әрбір айнымалысына сәйкес келетін n m шектеулер бар. Қос есептің шектеулеріндегі сол және оң жақ бөліктер арасындағы сәйкессіздік бастапқы есептің сәйкес айнымалысы үшін бағалау болып табылатынын еске сала отырып, ағымдағы тасымалдау жоспарының оңтайлылығының шарттарын ТЕ-ке жазамыз:
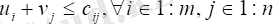
Белгісіз потенциалдар және (олардың жалпы саны m + n тең) негізгі айнымалылар үшін бағалаулар (кестенің толтырылған ұяшықтары) TЕ нөлге тең (бар m + n - 1) төмендегі ескертуден туындайтын осындай теңдіктер) .
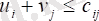
TЕ кестесінің толтырылған ұяшықтары (i, j) үшін.
Белгісіздердің бірі (жалпы айтқанда, кез келген) белгілі бір санға (сонымен қатар, жалпы айтқанда, кез келген) тең деп болжанған кезде алынған жүйенің шешімі (ол теңдеулер санынан біреуге көп белгісізді қамтиды) ізделеді. Осыдан кейін қалған жүйенің бірегей шешімі бар.
§2. Теориялық материал
2. 1 Транспорттық есептерінің жалпы тұжырымы
Көлік есептері сызықтық бағдарламалау есептерімен байланысты және оларды симплекс әдісімен шешуге болады. Дегенмен, көлік мәселесінің шектеулер жүйесінің матрицасы ерекше болғандықтан, оны шешудің арнайы әдістері жасалған. Бұл әдістер симплекс әдісі сияқты бастапқы анықтамалық шешімді табуға, содан кейін оны жетілдіре отырып, оңтайлы шешімді алуға мүмкіндік береді. Классикалық көліктік тапсырма үшін тапсырмалардың екі түрі ажыратылады: шығындар критерийі (тасымалдау шығындарының минимумына жету) немесе қашықтық және уақыт критерийі (тасымалдауға ең аз уақыт жұмсалады) . Көлік мәселесінің жалпы тұжырымы кейбір біртекті жүктерді m жөнелту (өндіріс) a1, a2, …an пунктінен n бағытқа (тұтыну) b1, b2, …, bn тасымалдаудың оңтайлы жоспарын анықтау болып табылады. Бұл жағдайда, әдетте, оңтайлылық критерийі ретінде не бүкіл жүкті тасымалдаудың ең аз құны немесе оны жеткізудің ең аз уақыты алынады. Сәйкесінше a1, a2, …an m базалардың (қорлардың) әрқайсысында қолжетімді жүк көлемін және қолжетімді жүктің жалпы көлемін a:
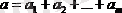 ; тұтынушылардың (қажеттіліктердің) әрқайсысының тапсырыстары сәйкесінше белгіленеді
; тұтынушылардың (қажеттіліктердің) әрқайсысының тапсырыстары сәйкесінше белгіленеді
 , ал қажеттіліктердің жалпы саны:
, ал қажеттіліктердің жалпы саны:
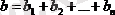 .
.
Содан кейін шарт бойынша бізде жабық үлгі, ал шарт бойынша көлік мәселесінің ашық үлгісі бар. Әлбетте, жабық модель жағдайында барлық қолда бар жүк толығымен тасымалданады және тұтынушылардың барлық қажеттіліктері толығымен қанағаттандырылады, ал ашық модельде барлық тұтынушылар қанағаттандырылады және сонымен бірге артық. Жүк кейбір базаларда қалады (a>b) немесе қажеттіліктер толығымен қанағаттандырылмаса да, бүкіл жүк таусылды (a<b) . Сондай-ақ, тасымалдау, мысалы, базадан немесе өндірушінің зауытынан тұтынушыға тікелей жүзеге асырылатын бір сатылы тапсырма үлгілері және олардың арасында «қайта тиеу пункті» бар екі сатылы модельдер бар, мысалы: қойма.
a=b немесе a≠b шарты көлік мәселесінің жабық үлгісімен немесе ашық үлгісімен айналысатынымызды білдіреді. xij айнымалысы базалық ai-дан тұтынушыға bj тасымалданатын жүк көлемін білдіреді, бұл мәндердің жиынтығы матрицаны (трафик матрицасын) құрайды. Әлбетте, xij айнымалысы шарттарды қанағаттандыруы керек:
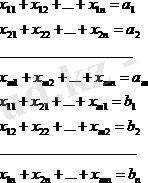
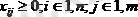 (4)
(4)
(4) жүйеде m*n белгісіздері бар m+n теңдеулері бар. Оның ерекшелігі белгісіздердің коэффициенттері барлық жерде бірге тең. Сонымен қатар (4) жүйенің барлық теңдеулерін екі топқа бөлуге болады: бірінші топ m бірінші теңдеу («көлденең» теңдеулер) және қалған n теңдеулердің екінші тобы («тік» теңдеулер) . Көлденең теңдеулердің әрқайсысында бірінші индексі бірдей белгісіздер бар (олар қозғалыс матрицасының бір жолын құрайды), тік теңдеулердің әрқайсысында бірдей екінші индексі бар белгісіздер бар (олар қозғалыс матрицасының бір бағанасын құрайды) . Осылайша, әрбір белгісіз (4) жүйеде екі рет кездеседі: бір және тек бір көлденең және бір және тек бір тік теңдеуде. Жүйенің бұл құрылымы (4) оның дәрежесін анықтауды жеңілдетеді. Шынында да, трафик матрицасының бірінші жолы мен бірінші бағанасын құрайтын белгісіздер жиынын негізге алуға болатынын көрсетейік. Базистің мұндай таңдауымен олардың екі индексінің кем дегенде біреуі біреуге тең, демек, бос белгісіздер i≥2, j≥2 шартымен анықталады. (4) жүйесін келесі түрде қайта жазайық:
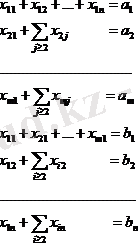 (5)
(5)
мұндағы таңбалар
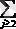 және
және
 сәйкес көрсеткіш бойынша қосындыны білдіреді. Мысалға:
сәйкес көрсеткіш бойынша қосындыны білдіреді. Мысалға:
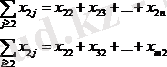 (6)
(6)
Мұндай қосындының таңбаларының астында тек бос белгісіздер ғана біріктірілетінін байқау қиын емес (мұнда i≥2, j≥2) . Біз қарастырып отырған жүйеде тек екі теңдеу, атап айтқанда, бірінші көлденең және бірінші тік, біз негіз құру үшін таңдағандардың ішінен бірден көп белгісізді қамтиды. Тік теңдеулерді пайдаланып бірінші көлденең теңдеуден x12, x13, …, x1n негізгі белгісіздерді алып тастап, мына теңдеуді аламыз:
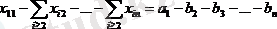 (7)
(7)
немесе қысқарақ
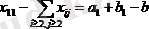 (8)
(8)
мұндағы
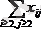 таңбасы барлық бос белгісіздердің қосындысын білдіреді. Сол сияқты көлденең теңдеулерді қолданып бірінші тік теңдеуден x21, x31, …, xm1 негізгі белгісіздерді алып тастап, теңдеуді аламыз:
таңбасы барлық бос белгісіздердің қосындысын білдіреді. Сол сияқты көлденең теңдеулерді қолданып бірінші тік теңдеуден x21, x31, …, xm1 негізгі белгісіздерді алып тастап, теңдеуді аламыз:
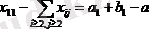 (9)
(9)
олардың біреуінен белгісіз x11-ді алып тастасақ, біз 0=0 теңдеуін аламыз, ол жойылады. жүйе. Сонымен, (7) жүйені түрлендіру екі теңдеуді (бірінші көлденең және бірінші тік) (8) теңдеуімен ауыстыруға дейін қысқартылды. Қалған теңдеулер өзгеріссіз қалады. Жүйе келесі пішінді алды:
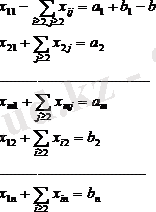 (10)
(10)
(10) жүйеде жоғарыдағы негіз таңдалады: бірінші n теңдеуден негізгі белгісіздер қозғалыс матрицасының бірінші бағанын құрайды, ал қалған теңдеулердің негізгі белгісіздері бірінші белгісіз x11 жоқ қозғалыс матрицасының бірінші жолын құрайды. (10) жүйенің бірінші теңдеуіне кіреді) . (10) жүйесінде m + n-1 теңдеулері бар, таңдалған негіз m + n-1 белгісізді қамтиды, демек, (7) жүйенің рангі m + n-1-ге тең болады. Тасымалдау мәселесін шешу үшін қорлар мен қажеттіліктерден басқа cij тарифтерін білу қажет, яғни жүк бірлігін базалық ai-дан тұтынушыға bj дейін тасымалдау құнын білу қажет. cij тарифтер жиынтығы трафик матрицасы мен қор және сұраныс деректерімен бір кестеге біріктірілетін матрицаны да құрайды. Тарифтер жиынтығы Барлық шығындардың сомасы, яғни осы тасымалдау жоспарын жүзеге асыру құны, xij айнымалыларының сызықтық функциясы болып табылады:
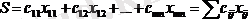 (11)
(11)
Ол теңдеулер жүйесінің рұқсат етілген шешімдері аймағында қажет (7) және (6) сызықтық функцияны (11) кішірейтетін шешімін табу. Осылайша, тасымалдау мәселесі сызықтық бағдарламалау мәселесі екенін көреміз. Оны шешу үшін симплекс әдісі де қолданылады, бірақ мәселенің ерекшелігіне байланысты мұнда симплекс кестелерінен бас тартуға болады. Шешімді тасымалдау кестесін кейбір түрлендірулер арқылы алуға болады. Бұл трансформациялар бір тасымалдау жоспарынан екіншісіне өтуге сәйкес келеді. Бірақ, жалпы жағдайдағыдай, негізгі шешімдердің ішінен оңтайлы шешім ізделеді. Сондықтан біз тек негізгі (немесе қосалқы) жоспарлармен айналысамыз. Бұл жағдайда теңдеулер жүйесінің рангі m + n-1-ге тең болғандықтан, барлық m * n белгісіздердің ішінен xij, m + n-1 негізгі белгісіздер ажыратылады, ал қалған (m-1) * (n) -1) белгісіздер бос. Негізгі шешімде бос белгісіздер нөлге тең. Әдетте бұл нөлдер кестеге енгізілмейді, сәйкес ұяшықтар бос қалады. Осылайша, негізгі жоспарды білдіретін тасымалдау кестесінде бізде m+n-1 толтырылған және (m-1) *(n-1) бос ұяшықтар бар. Бақылау үшін тасымалдау кестесінің әрбір жолының толтырылған ұяшықтарындағы сандардың қосындысы сәйкес базадағы жүк қорына тең екендігін, ал әрбір бағандағы тапсырыс берушінің қажеттіліктеріне тең екендігін тексеру қажет (бұл бұл жоспардың (5) жүйесіне шешім екенін растайды) . 1-ескертпе: бұл жерде азғындау жағдайлары жоққа шығарылмайды, яғни бір немесе бірнеше негізгі белгісіздердің жойылу мүмкіндігі. Бірақ бұл нөлдер, бос белгісіздердің нөлдерінен айырмашылығы, сәйкес ұяшыққа сәйкес келеді және бұл ұяшық толтырылған болып саналады. 2-ескертпе: cij мәндері арқылы тек тарифтерді айтудың қажеті жоқ екені анық. Сіз сондай-ақ оларды тарифтерге пропорционалды мәндер ретінде қарастыра аласыз, мысалы, базадан тұтынушыларға дейінгі қашықтық. Егер, мысалы, xij тоннамен және cij километрмен өрнектелсе, онда (11) формула бойынша анықталатын S мәні осы тасымалдау жоспарының көлемін құрайтын тонна-километрлердің саны болып табылады. Әлбетте, тасымалдау шығындары тонна-километрлер санына пропорционалды және, демек, S минимумында минималды болады. Бұл жағдайда тарифтік матрицаның орнына бізде қашықтық матрицасы бар.
2. 1 Транспорттық есептің негізгі жоспарын құру әдістері
Тасымалдау тапсырмасы үшін негізгі сызықты табудың көптеген әдістері бар, мысалы: «Қос артықшылық әдісі», «Ең аз оңтайлылық критерийі әдісі», «Алға жүгіру әдісі», бірақ ең маңыздылары «Солтүстік-батыс бұрышы» болып табылады. және «Ең аз элемент әдісі». «Солтүстік-батыс бұрыш әдісі» көлік мәселесінің ерікті негізгі жоспарын табу үшін қолданылады, ал «минималды элемент әдісі» тасымалдау мәселесінің бастапқы негізгі жоспарын құруға мүмкіндік береді және солтүстік-батыс бұрыш әдісінің нұсқасы болып табылады, ол С=(Сij) mn матрицасының ерекшеліктерін ескеріңіз. Солтүстік-батыс бұрыштық әдіске қарағанда, бұл әдіс жеткілікті үнемді жоспарды дереу алуға мүмкіндік береді және оны оңтайландыру үшін итерациялардың жалпы санын азайтады.
2. 2 Минималды элемент әдісі
Әдістің мәні мынада: барлық шығындар кестесінің ең кішісі таңдалып, оған сәйкес ұяшыққа ai және bj сандарының ең кішісі орналастырылады. Содан кейін, не қорлары толығымен пайдаланылған жеткізушіге сәйкес келетін жол, немесе қажеттіліктері толығымен қанағаттандырылған тұтынушыға сәйкес келетін баған немесе жеткізушінің қорлары пайдаланылған болса және тұтынушының қажеттіліктері болса, жол мен бағанның екеуі де. қанағаттандырылды, қараудан шығарылады. Шығындар кестесінің қалған бөлігінен ең төменгі құн қайтадан таңдалады және қорларды бөлу процесі барлық қорлар бөлінгенге және талаптар қанағаттандырылғанға дейін жалғасады.
2. 3 Потенциалдар әдісі
Транспорттық есепті шешудің бұл бірінші нақты әдісін 1949 жылы Кантарович А. В. және Гавурин М. К. мәні бойынша, бұл көлік мәселесіне қатысты жоспарды дәйекті жетілдіру әдісін егжей-тегжейлі көрсету. Дегенмен, басында ол сызықтық бағдарламалаудың жалпы әдістерінен тыс ұсынылды. Біраз уақыттан кейін ұқсас алгоритмді сызықтық бағдарламалаудың жалпы идеясына негізделген Данзиом әзірледі. Американдық әдебиетте оны әдетте модификацияланған дистрибутив әдісі деп атайды. Потенциалдар әдісі қандай да бір негізгі тасымалдау жоспарынан бастап, шектеулі қадамдар (итерациялар) ішінде тасымалдау мәселесінің шешімін құруға мүмкіндік береді. Көлік есебінің оптималды жоспарын осы әдіспен анықтаудың жалпы принципі сызықтық программалау есебін симплекс әдісімен шешу принципіне ұқсас, атап айтқанда: біріншіден, көлік есебінің негізгі жоспары табылады, содан кейін ол оңтайлы жоспар алынғанға дейін дәйекті түрде жетілдіріледі.
Потенциалдар әдісі - бұл тасымалдау есебінің ерекшелігін ескеретін симплекс әдісінің модификациясы, сондықтан оның алгоритмі шешімдер жиынында мақсат функциясының шектелмегендігін тексеру қадамын қоспағанда, симплекс әдісінің алгоритмінен айырмашылығы жоқ. Потенциалдар әдісінде бұл қадамның болмауы тұйық ТЕ әрқашан шешілетін теоремаға байланысты. Сонымен, ТЕ шешудің потенциалдар әдісінің алгоритмі келесі қадамдардан тұрады:
1-ҚАДАМ. Бастапқы тасымалдау жоспарын құру.
2-ҚАДАМ. Ағымдағы жоспардың оңтайлылығын тексеру.
Егер жоспар оңтайлы болса, онда алгоритм аяқталған болады.
3-ҚАДАМ. Тасымалдау жоспарын жетілдіру. 1-қадамға өту.
Әр қадамды суреттей отырып, алгоритмді кезең-кезеңімен сипаттап көрейік
1-ҚАДАМ. Бастапқы тасымалдау жоспарын құру.
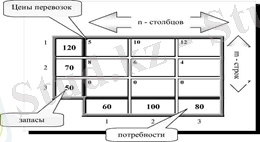
Бастапқы шешімнің құрылымы (сонымен қатар кейінгі есептеулер) келесідей кестеде жүзеге асырылады(1-кесте) :
қажеттіліктер
Тасымал құны
қор
m-жол
n- баған
1-кесте. Бастапқы шешімнің құрылымы
Кестенің ұяшығы (i, j) i-ші жеткізушіні j-ші тұтынушымен байланыстыратын байланысқа сәйкес келеді.
Бастапқы тасымалдау жоспарын құру кестенің ұяшықтарына трафик көлемін келесідей етіп тағайындауды білдіреді:
а) толтырылған ұяшықтар саны (m + n-1) болды. (Содан кейін тасымалдау жоспары СБМ негізгі шешіміне сәйкес келеді) ;
б) кез келген қатардағы жөнелтілімдер сомасы сәйкес жеткізушінің қорына, ал әрбір бағандағы жөнелтілімдер сомасы тұтынушының сұранысына тең болуы керек. (ТЕ шектеулерін орындау шарты) . Бастапқы шешімді табудың бірнеше жолы бар, олар тек келесі тасымалдау тағайындалған ұяшықты таңдауда ғана ерекшеленеді. Сонымен, солтүстік-батыс бұрыш (СББ) әдісінде кестенің жоғарғы сол жақ ұяшығы келесі тасымалдау бағыты үшін таңдалады (бұл ретте тасымалдау бағасы ешбір жағдайда есепке алынбайды) . Керісінше, минималды шығын әдісінде толтыру үшін ең төменгі тасымалдау бағасы бар ағымдағы кестенің ұяшығы таңдалады, бұл көп жағдайда (бірақ әрқашан емес) бастапқы арзанырақ (сондықтан оңтайлыға жақын) тасымалдау жоспарына әкеледі.
Біз минималды шығын әдісін қолданамыз.
Енді бастапқы шешімді табу алгоритмін сипаттайық.
1-ҚАДАМ. Белгілі бір жолмен ағымдағы кестедегі ұяшықты таңдаңыз. Оның индекстері (i, j) болсын (i - жеткізушінің нөмірі, j - тұтынушының нөмірі) .
2-ҚАДАМ. Осы ұяшыққа тасымалдау ретінде біз ең кіші ai мен қажет bj тағайындаймыз.
xij = мин {ai, bj}
3-ҚАДАМ. ai қорын және bj сұранысын xij тасымалдау көлеміне азайтыңыз, яғни.
ai = ai - xij,
bj=bj-xij
4-ҚАДАМ. Қор таусылғанда (ai = 0), біз i-ші қатардың қалған бос ұяшықтарын тасымалдауға тыйым саламыз және сұраныс таусылған кезде
(bj =0) j-ші бағандағы бірдей ұяшықтарға тыйым саламыз.
Сұраныс қорлары бір мезгілде таусылған жағдайда (ai =bj = 0), біз не қатарда тасымалдауға тыйым саламыз (бұл жағдайда тұтынушыда қанағаттандырылуы тиіс нөлге тең мөлшердегі қажеттілік бар деп есептейміз) немесе бағанында (бұл жағдайда жеткізушіде нөлге тең қор бар деп есептейміз, оны шығару керек) . Бұл қатар мен бағанда тасымалдауға бір мезгілде тыйым салынған кезде кестедегі толтырылған ұяшықтар саны m + n-1-ден кем болмауы үшін жасалады.
Толтырылған және тыйым салынған ұяшықтарды қамтымайтын жаңа ағымдағы кестені алайық (2-кесте) . Кесте бос болмаса, 1-қадамға өтіңіз. (Кесте таусылғанда, аяқтаңыз) .
Минималды шығындар әдісі.
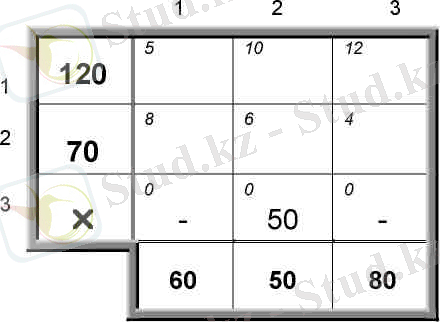
2-кесте.
1. Ең төменгі бағасы бар ұяшықтар (3. 1), (3. 2) және (3. 3) . Біз, мысалы, (3, 2) таңдаймыз. (бұдан әрі барлық қадамдар, алдыңғы әдістегідей) .
2. = мин {50, 60} = 50
3. =50-50=0, = 100-50=50
4. 3-жолға тыйым салу. (3- кесте)

3-кесте
- Min бағасы бар ұяшық ~ (2, 3)
- x23= min{70, 80} = 70
- a2=70-70=0, b'3= 80-70=10
- 3-жолға тыйым салу. (4- кесте)
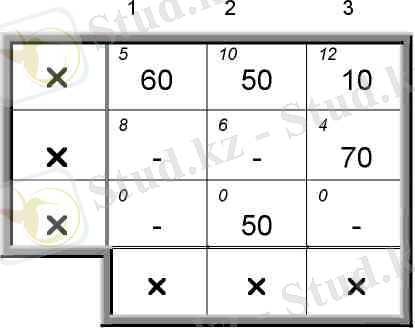
5
60
8
-
6
-
4
70
0
50
0
-
4-кесте
1. Минималды бағасы бар ұяшық ~ (1, 1)
2. =мин{120, 60} = 60
3. =120-60 = 60, = 0
4. Бірінші бағанда тыйым салатын ештеңе жоқ. Ағымдағы кестеде екі ұяшық (1, 2) және (1, 3) бар. (5-кесте)
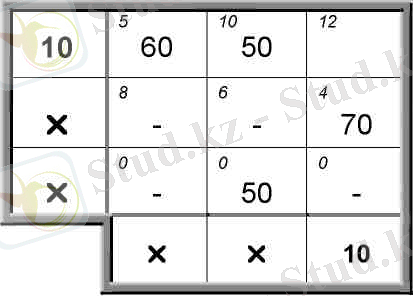
5-кесте
1. Ұяшықты таңдаңыз (1, 2)
2. =мин{110, 100} = 100
3. =110-100=10, =0
4. Ағымдағы кестеде бір ұяшық бар (1, 3) . (6-кесте)
6-кесте
1. Соңғы ұяшықты таңдаңыз (1, 3)
2. =мин{10, 10} = 10
3. = = 0
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz