Екі жазықтықтың кеңістікте өз ара орналасуы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

№6 Дәріс. Екі жазықтықтың кеңістікте өз ара орналасуы.

Қарастырылатын сұрақтар:

Параллель жазықтықтар;
Қиылысушы жазықтықтар;
Өзара перпендикуляр жазықтықтар

еКІ ЖАЗЫҚТЫҚТЫҢ ӨЗАРА ОРНАЛАСУ ЖАҒДАЙЫ

Екі жазықтық кеңістікте бірі-біріне параллель болуы мүмкін немесе қиылысуы мүмкін. Өзара перпендикуляр жазықтықтар қиылысушы жазықтықтардың жеке жағдайы болып табылады.

1. Параллель жазықтықтар . Егер бір жазықтықтың қиылысушы екі түзуі, сәйкесінше басқа жазықтықтағы түзулерге параллель болса, онда жазықтықтар параллель.

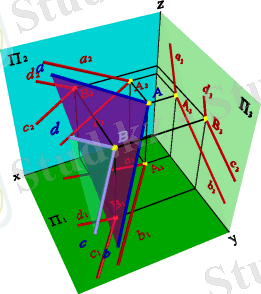
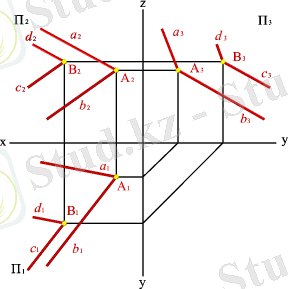
Бұл анықтама келесі есепке сәйкестендіріледі, В нүктесі арқылы берілген жазықтыққа параллель жазықтық жүргіземіз, жазықтық α( a, b) қиылысушы екі түзулер арқылы берілген (5. 24. - сурет) .

Есеп. Берілген: α( a, b қиылысушы түзулері арқылы берілген жалпы жағдайдағы жазықтық және В нүктесі берілген .

α( a, b жазықтығына параллель В нүктесі арқылы берілген жазықтықты жүргізіп, оны екі қиылысушы c мен d түзулері арқылы беру керек.

Анықтамаға сәйкес егер бір жазықтықтың екі қиылысушы түзуі басқа жазықтықтағы екі қиылысушы түзуге параллель болса, онда бұл жазықтықтар өзара параллель болады.

Эпюрде параллель түзулер жүргізу үшін параллель проекциялаудың қасиеттерін қолдану керек - параллель түзулердің проекциясы өзара параллель болады.

d // a , с // b €⇒ δ ₁ // α ₁ , с ₁ // b ₁ ; δ ₂ // α ₂ , с ₂ // b ₂ ; δ ₃ // α ₃ , с ₃ // b ₃ .

: 5. 24. - Сурет. Параллель жазықтықтар

2. Қиылысушы жазықтықтар , жеке жағдайы - өзара перпендикуляр жазықтықтар. Екі жазықтықтың қиылысу сызығы түзу болады, оны тұрғызу үшін екі жазықтықтың ортақ екі нүктесін, немесе бір нүктесін және жазықтықтар қиылысу сызығының бағытын тапса жеткілікті.

Екі жазықтықтың қиылысу сызығын тұрғызу керек, егер олардың біреуі проекциялаушы болса (5. 25. - сурет) .

Есеп. Берілген: АВС үшбұрышы мен жалпы жазықтық берілген, ал екінші α жазықтығы горизонталь проекциялаушы.

: 5. 25. - Сурет. Жалпы жағдайдағы жазықтық пен горизонтальды проекциялаушы жазықтықтың қиылысуы

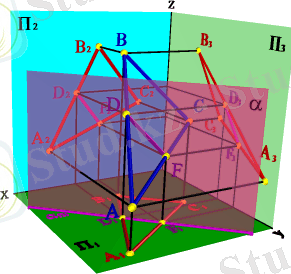
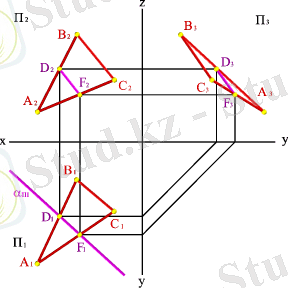
Жазықтықтың қиылысу сызығын тұрғызу қажет болсын.

Есепті шешу үшін осы жазықтықтарға түзу сызық жүргізуге болатын, ортақ екі нүктені табу қажет. АВС үшбұрышымен берілген жазықтықты АВ , АС , ВС түзулері ретінде қарастыруға болады. АВ түзуімен α жазықтығының қиылысу нүктесі - D нүктесі, ( AС ) түзуінің қиылысу нүктесі - F . [ DF ] кесіндісі - жазықтықтың қиылысу сызығын анықтайды. α горизонталь проекциялаушы жазықтық болғандықтан, D ₁ F ₁ проекциялары α _П1  жазықтығының ізімен сәйкес келеді, сондықтан DF - тің П ₂ және П ₃ -те жетіспей тұрған проекцияларын тұрғызу қажет.

Жалпы жағдайға өтелік. Кеңістікте жалпы жағдайдағы екі жазықтық берілсін: α ( ν, μ ) және β ( ABC ) (5. 26. - сурет) .

: 5. 26. - Сурет. Жалпы жағдайдағы жазықтықтардың қиылысуы

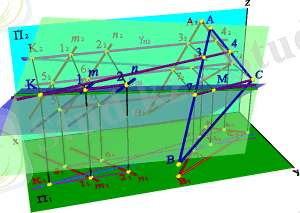
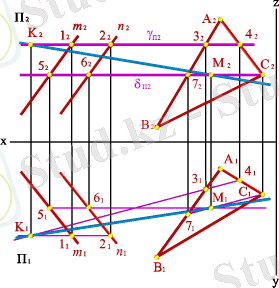
α(m//n) және β( АВС ) жазықтықтарының қиылысу сызығын тұрғызуды қарастырайық. Берілген жазықтық қиылысу тұрғызу үшін көмекші қиюшы жазықтықтар γ және δ жүргіземіз. Осы жазықтықпен қарастырып отырған жазықтықтың қиылысу сызығын табамыз. γ жазықтығы α жазықтығын ( 1, 2 ) түзуі бойынша, ал β жазықтығы ( 3, 4 ) түзуі бойынша қияды. К нүктесі - осы түзудің қиылысу нүктесі бір уақытта α, β және γ жазықтықтарына тиісті болады, сонымен қатар, α мен β жазықтықтарының қиылысу сызығына тиісті. δ жазықтығы α мен β жазықтықтарын ( 56 ) және ( 7C ) түзулері бойынша қияды, олардың М қиылысу нүктесі біруақытта α, β, δ жазықтықтарында орналасқан және α мен β жазықтықтарының қиылысу түзу сызығына тиісті. Осы арқылы α мен β жазықтықтарының қиылысу сызығына тиісті екі нүктесі табылады- ( КМ ) - түзуі.

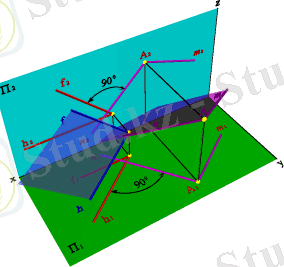
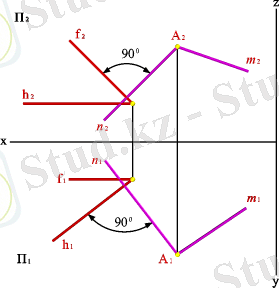
Өзара перпендикуляр жазықтықтар болатындығы . стереометриядан белгілі. Екі жазықтық өзара перпендикуляр, егер олардың біреуі перпендикуляр арқылы басқасына өтсе. онда А нүктесі арқылы берілген α(f, h) жазықтығына перпендикуляр жазықтықтар жиынын жүргізге болады. Өсі А нүктесінен α жазықтығына түсірілген перпендикуляр болатын бұл жазықтықтар кеңістікте жазықтықтар шоғырын құрайды. А нүктесінен hf жазықтығына перпендикуляр болатын n түзуін жүргізу қажет ( n - нің горизонталь проекциясы h горизонталінің горизонталь проекциясына перпендикуляр, n - нің фронталь проекциясы f фронталінің фронталь проекциясына перпендикуляр) . n түзуі арқылы өтетін кез-келген жазықтық hf жазықтығына перпендикуляр, сондықтан А нүктесі арқылы жазықтық жүргізу үшін кез-келген m түзуін жүргіземіз. mn екі қиылысушы түзулері арқылы берілген жазықтық hf жазықтығына перпендикуляр болады (5. 27. - сурет) .