7-9 сынып геометрия курсындағы салу есептерін оқыту және шешу әдістемесі


Тақырыбы: 7-9 сынып геометрия курсындағы салу есептері
Кіріспе
Геометрия - өте ерте кездерде пайда болып, әрі дамыған пәндердің бірі екенін оқушы 7 - ші сыныптың «Геометрия» оқулығынан мәлімет ала алады. Аталмыш кітаптарда геометрияның адамзат баласының күнделікті өмірде, демек практикалық жұмыстарда қолданылуы туралы да айтылған. Қазіргі заманда геометрияның ролі не себепті төмендеп кетті? Геометрия ұғымдарымен оқушылар тек 7 - ші сыныптан бастап танысады. Бұл пәннің ең қарапайым фигураларымен, (дөңгелек шар, төртбұрыш, үшбұрышпен) тіпті, жас нәресте кезімізден таныс болып, оларды күнделікті көріп, біліп, пайдаланып жүргенімізді байқамаймыз, оларға мән де бере қоймаймыз. Ал ас ішкенде көретін, ұстайтын заттары: кесенің, құлақшынның (бокал), тәрелкенің шеттері мен түбі, қуыршағының не өзінің арбаларының дөңгелектері, төбедегі шам, телевизор, есік - терезе, қабырға т. б. ; демек баланы қоршаған ортада толып жатқан заттар геометриялық фигуралар екендігіне мән бере бермейміз. Яғни баланың тіпті тілі шықпай - ақ, санауға үйренбей жатып, цифрлармен таныспай тұрып-ақ геометриялық фигуралармен таныс. Одан арғысы бала - бақша мен бастауыш мектепте тәрбиеші мен мұғалім математикалық қарапайым артық - кем, үлкен - кіші, қанша болса, сонша сияқты түсініктерді немесе қосу - азайту амалдарын түсіндіргенде жолақты полотнаға көбінесе геометриялық фигураларды пайдаланады. Айтарымыз, осыншама уақыт геометриямен танысып келген оқушы, 7 - ші сыныптан бастап геометрияның жүйелі курсы басталғанда, не себепті оған геометрия ең қиын пәндердің бірі болып шыға келеді?! Оқушылар алгебралық өрнектерді, теңдеулерді, қысқаша көбейту формулалары, қосу мен азайтудың көбейту мен бөлуге қатысты үлестірімділік тәрізді заңдарына сүйеніп жеңіл түрде орындай алса, геометрия аксиомаларын қолданып теоремаларды дәлелдеуге, есептер шығаруға не себепті қиналады? Осы қиындықтардың туу себептері неде және оны шешу жолдары қандай? -деген сауал әр мұғалімді ойландырары сөзсіз.
Зерттеу өзектілігі: Оқушылардың шығармашылық қабілеттерін арттыруда математика ерекше роль атқарады. Математиканың негізгі мақсаты-ойлауды, абстрактілі ойлауды қалыптастыру. Оқу үрдісінде, ең алдымен, логикалық ойлау, алгоритмдік ойлау, конструктивтілік, сын тұрғысынан ойлау және тағы басқа ойлау қабілеттері дамиды. Математикалық қабілеттерін дамытуда геометрияның оқыту үрдісінде алатын орны ерекше. Қазіргі заман техникасы бұл салуларды кез келген адамнан әлде қайда тез, әлі дәлірек орындау мүмкіндігін, сонымен қатар, циркуль мен сызғышты қолданып шешуге мүмкін емес салу есептерін шешу мүмкіндігін туғызып отыр. Солай бола тұрса да салу есептерінсіз геометрия, геометрия болудан қалады. Геометрияны шын мәнінде жақсы сезіну үшін, оны жақсы көріп, ұнату үшін, салу есептерін айналып өтуге болмайды. Осы уақытқа дейін байқағаным, қалалық, облыстық олимпиадаларда, жоғарғы оқу орындарына түсу емтихандарында геометриялық салу есептерін шешу мектеп оқушыларына өте үлкен қиындықтар туғызады. Олар есептің жалпы шешу жолдарын білмейді, шешу әдістерін қолдана алмайды немесе жеткіліксіз қолданады. Салу есептеріне білім мен дағдының дамуының жоғары дайындық деңгейінің жетіспеушілігінің негізгі себептері:
- Геометрияның жалған түрде қабылдануы;
- Геометриялық фигураларды салуда, өлшеуде және модельдеуде планиметрияның мәселелерін оқытуда белгілі бір сипаттың жоқтығы,
- 5-6 сыныптарда геометрия курсын оқытуда, оның ішінде салу есептерінің элементтерін үйрену дайындықтарының болмауы;
Жоғарыда айтылғандардан осы тақырыптың өзекті екендігі белгілі.
Зерттеу пәні: 7-9 сынып геометрия курсындағы салу есептері
Мақсаты: Оқушылардың математикалық қабілеттіліктерін дамыту негізінде геометрия курсындағы салу есептерін оқытудың әдістемелік қағидаларын құрастыру
Күтілетін нәтижелер:
-Мектептегі геометрияға берілген сағат санын ұлғайту;
-Оқушылардың кеңістікті болжауын, елестетуін 10-сыныпка дейін күтпей - ак ертерек бастау;
-Көрнекіліктерді мейлінше көбірек пайдалану, мүмкіндігінше өздеріне де жасату;
-Аксиомалар мен теоремалардың, есеп шарттарын модельдерді қолданып, мағынасын жете меңгерту;
-Жоғары оқу орындарында геометрияны оқытуға баса көніл аудару;
-Геометриялық ұғымдарға байланысты өздік жұмыстар, мақалалар, жобалар, құрып оларды топтарда талқылап отыру;
-ҰБТ - дағы геометрия есептерінің санын көбейту;
-Мектепке геометрия пәнінен емтихан енгізу.
-Салу есептерін шешудің жалпы әдістерін белгілеу және осы әдістер оқушыларға 5-7 сыныптарда үйрету;
-Салуға берілген есептер жүйесіне шығармашылық компоненттер енгізу;
1. 1ҚАРАПАЙЫМ САЛУ ЕСЕПТЕРІ
Геометрияда «Салу есептері» деп аталатын ерекше есептер бар. Салу есептері сызу құралдарының көмегімен орындалады. Салу есебінің шартында геометриялық фигураны салу талап етіледі. Фигураны салумен есеп шешілді деуге болмайды. Салу есептерін шешу процесінде мұғалім оқушылардың алгоритмдік мәдениетінің элементтерін ұтымды қалыптастыра алады. Салу есептері, тіпті олардың ең қарапайым есебінің өзі негізгі геометриялық фигура туралы теориялық мәліметтерді терең тануға мүмкіндік береді. Осы есептерді шешу процесінде оқушы оқу материалының моделін елестетіп, осы модельмен жұмыс жасайды. Есепті шешу үшін есептің мазмұнын мұқият түсініп, берілген және салынатын фигуралардың арасындағы байланысты ескере отырып, фигураны қалай салуға болатынын біліп алу керек. Салуды неден бастаймыз, алдымен нені саламыз, одан соң нені саламыз, тағы сол сияқты. Салу есептерін шешуде көбінесе сызғыш пайдаланып:
- берілген нүкте арқылы өтетін түзулерді жүргізуге болады;
- берілген екі нүкте арқылы түзу жүргізуге болады;
- кез келген түзуді жүргізуге болады;
Осылардан басқа ешқандай салу жұмыстарын орындауға сызғыштың мүмкіндігі жоқ. Циркульді пайдаланып:
- берілген нүктені центр етіп алып, радиусы берілген кесіндіге тең шеңбер салуға болады;
- берілген кесіндіге тең кесінді салуға болады.
Салу есептерінің бірнешеуін қарастырсақ:
- Берілген бұрышқа тең бұрыш салу,
- Берілген бұрыштың биссектрисасын салу,
- Кесіндіні қақ бөлу,
- Берілген нүктеден тҥзуге перпендикуляр түсіру.
Қандай да бір салу есебінің бірнеше шешімі болуы мүмкін, яғни есептің барлық шартын қанағатандыратын әр түрлі фигуралар бар. Салу есебін шешу - есептің барлық шешімін табуды білдіреді. Бұл анықтама кейбір түсініктемелерді талап етеді. Есеп шартын қанағаттандыратын фигуралар пішінімен және өлшемдерімен ерекшеленсе, сол сияқты жазықтықтағы орнымен ерекшеленеді. Мысалы, қарапайым есепті қарастырайық:
Екі қабырғасы және олардың арасындағы бұрыш бойынша үшбұрыш салу.
Бұл есептің дәл мағынасы келесіде: екі қабырғасы, сәйкесінше, берілген екі кесіндіге, ал олардың арасындағы бұрыш берілген бұрышқа тең болатындай үшбұрыш салу, мұнда ізделінді фигура (үшбұрыш) берілген фигуралармен ( екі кесінді және бұрыш) тек теңдік арақатынасымен байланысты, ізделінді фигураның орналасуы басқа фигурамен салыстырғанда талғаусыз. Бұл жағдайда есеп шартын қанағаттандыратын үшбұрышын салу оңай. үшбұрышына тең барлық үшбұрыштар есеп шарттарын қанағаттандырады. Бірақ бұл үшбұрыштарды берілген есептің әр түрлі шешімдері ретінде қарастырудың мағынасы жоқ, өйткені олар бір-бірімен тек жазықтықта орналасуымен ерекшеленеді. Сондықтан есептің бір ғана шешімі бар деп есептейміз. Күрделі есептердің шешіміне жиі құрама бөліктері ретінде кіретін көптеген қарапайым геометриялық салу есептері бар. Мұндай текті есептер, әдетте, мектеп курсындағы геометрияның бірінші тарауларында қарастырылады. Элементар есептер қатарына кесілер жатады:
1. Берілген кесіндіні қақ бөлу.
2. Берілген бұрышты қақ бөлу.
3. Берілген түзуде берілген кесіндіге тең кесінді салу.
4. Берілген бұрышқа тең бұрыш салу.
5. Берілген нүкте арқылы өтетін, берілген түзуге параллель түзу салу.
6. Берілген нүкте арқылы өтетін, берілген түзуге перпендикуляр түзу салу.
7. Берілген қатынаста кесіндіні қақ бөлу.
8. Үш қабырғасы бойынша үшбұрыш салу.
9. Бір қабырғасы және іргелес жатқан екі бұрышы бойынша үшбұрыш салу.
10. Екі қабырғасы және олар арасындағы бұрыш бойынша үшбұрыш салу керек.
Бұл элементар есептердің толық шешімдерін біз циркуль және сызғыш көмегімен құрамыз.
Мысалдар қарастырайық:
1 - мысал . Берілген бұрышқа тең бұрыш салу. Ең алдымен есепті қалай түсіну керек екенін айқындап алу керек, яғни не берілді және нені салу қажет екеніне жауап берейік. Төбесі О нүктесінде болатын (pq) бұрышы берілген. Онда циркульді және сызғышты пайдаланып, берілген (pq) бұрышына тең BAC бұрышын салу қажет. Ол үшін О центрінен радиусы кез келген шеңбер жүргіземіз. Бұл шеңбердің p және q түзулерімен қиылысу нүктелерін сәйкесінше P және Q арқылы белгілейік. Бастапқы нҥктесі А болатын кез келген а сәулесін алып, центрі А және радиусы ОР-ға тең шеңбер жүргіземіз. Бұл шеңбер а сәулесін В нүктесінде қиып өтсін. Осы шеңберді, яғни А, радиусы РО-ға тең шеңберді ω(А; РО) арқылы белгілейік. Сонымен, В= а∩ω (А; РО) . Енді келесі ω(В; PQ) шеңберін жүргізейік. (центрі В, радиусы PQ) . ω(А; РО) және ω(B; PQ) шеңберлерінің қиылысу нүктелерін С арқылы белгілейміз. Онда ВАС - бізге қажетті бұрыш. Шынында да, ∆ OPQ= ∆ ABC, өйткені салуымыз бойынша AB=OP, AC=OQ, BC=PQ. Олай болса, POQ= BAC.

2 - мысал . Берілген бҧрыштың биссектрисасын салу. Төбесі А болатын (ab) бұрышы берілсін. ω (A; r) шеңберін жүргіземіз, r - кез келген оң сан. В = a ∩ ω(A; r) және C = b ∩ ω(A; r) нүктелерін аламыз. Енді ω (B; r) және ω (C; r) шеңберлерін жүргізіп, олардың қиылысу нүктесін D арқылы белгілейміз. Онда AD сәулесі (ab) бұрышының биссектрисасы болады. Бұл тұжырым ABD= ACD теңдігінен шығады. (2-сурет)

3 - мысал . Кесіндіні қақ бөлу. АВ кесіндісі берілсін. Кез келген r(r>АВ/2) радиусын алып, ω(A; r) және ω(B; r) шеңберлерін жүргіземіз. Бұл шеңберлер С және D нҥктелерінде қиылысатын болсын. Онда O=AB∩СD нҥктесі - АВ кесіндісінің ортасы: AO=OB. Шынында да, ACD және BDC үшбұрыштары тең бүйірлі және өзара тең (үш қабырғасы бойынша) . Осыдан ACD=BCD теңдігі шығады, яғни СО - АСВ тең бүйірлі үшбұрышының биссектрисасы. Олай болса, СО осы үшбұрыштың медианасы да болады. Онда AO=OB. (3-сурет)
4 - мысал . Берілген О нүктесі арқылы берілген а түзуіне перпендикуляр түзу жүргізу қажет. Екі жағдай қарастырамыз: 1) О € а; 2) О € а.
1) О€ а болсын. Радиусы кез келген ω(O; r) шеңберін жүргізіп, оның түзуімен қиылысуын А және В арқылы белгілейік. Радиустары r1, (r1>r) бірдей ω(A; r1) және ω(B; r1) шеңберлерін жүргіземіз. Бұл шеңберлердің қиылысу нҥктесін С арқылы белгілейік. Онда ОС бізге қажет тҥзу, яғни, ОС┴ а. Шынында да, ∆ АОС= ∆ BOC (үш қабырғасы бойынша), онда АОС= BOC (үш қабырғасы бойынша), онда ∟ AOC= ∟ BOC= 900 . (4-сурет)

2) О € а болсын. А түзуін А және В нҥктелерінде қиятын ω(O; r) шеңберін жүргіземіз. Енді ω (A; r) және ω (B; r) шеңберлері О және О1 нүктелерінде қиылысады. Онда ОО1 а. Шынында да, АОВ= AO1В (үш қабырғасы бойынша) . Онда OAB= O1АВ және үшбұрыштар теңдігінің 1 белгісі бойынша ∆ АОС= ∆ AO1С. Мұнда С=OO1∩ a. Сондықтан ACO= ACO1=90градус. (5-сурет)
1. 2Планиметриядағы салу есептері
Салу есептері оқушылардың геометриялық есептеулерін толығымен қалыптастырудың маңызды құралы болып табылады. Геометриялық салуларды орындау процесі кезінде оқушылар геометриялық фигуралар және олардың арасындағы қатынастар қасиеттерімен танысады, сызбалық құралдарды қолдануды үйренеді, графикалық дағдыларды қалыптастырады. Көптеген математикалық тұжырымдардың дұрыстығына оқушылар көптеген жағдайда геометриялық салулар процесінде көз жеткізеді.
Қазіргі уақытта геометриялық салу есептері кейбіреулерге қызықсық, қажетсіз, ойдан шығарылған болып көрінуі де мүмкін. Циркуль мен сызғышты пайдаланып дұрыс он жетібұрышты көпбұрыш салу, үш биіктігі бойынша үшбұрыш салу немесе берілген түзуге параллель түзу салу не үшін қажет?
Оқушылардың планиметриядағы салу есептерін шешу қабілеті мен білігін жүйелі қалыптастыруда Geogebra математикалық бағдарламасының көмегіне де жүгінуге болады. Осы бағдарлама арқылы салу есептерін қалай орындауға болатындығына тоқталамыз.
Geogebra (www. geogebra. org) тегін интерактивті математикалық орта (ИМО) болып табылады. Планиметрия курсының сызбаларын, әсіресе, сызғыш пен циркуль көмегімен салынатын есептерді салуда пайдасы көп. Бағдарлама толығымен қазақ тіліне аударылған.
 Әлемдегі ең танымал математикалық интерактивті бағдарлама ретінде танылған GeoGebra көптеген марапаттау мен сыйларға ие болды. Сонымен қатар STEM оқытуға және дүние жүзі бойынша білім берудегі инновациаларға қолдау білдіреді. 2013 жылдың маусымында Еуропалық заманауи білім беруге арналған журналында (European Journal of Contemporary Education, ISSN 2304-9650), GeoGebra бағдарламасын оқу процесінде пайдалану мүмкіндіктеріне арналған арнайлы басылым шықты (шақырылған редколлегия: п. ғ. д Дэниэл Джарвис, Университет Ниписсинг, Канада және ф-м. ғ. к Рушан Зиатдинов, Университет Фатих, Стамбул, Турция) .
Әлемдегі ең танымал математикалық интерактивті бағдарлама ретінде танылған GeoGebra көптеген марапаттау мен сыйларға ие болды. Сонымен қатар STEM оқытуға және дүние жүзі бойынша білім берудегі инновациаларға қолдау білдіреді. 2013 жылдың маусымында Еуропалық заманауи білім беруге арналған журналында (European Journal of Contemporary Education, ISSN 2304-9650), GeoGebra бағдарламасын оқу процесінде пайдалану мүмкіндіктеріне арналған арнайлы басылым шықты (шақырылған редколлегия: п. ғ. д Дэниэл Джарвис, Университет Ниписсинг, Канада және ф-м. ғ. к Рушан Зиатдинов, Университет Фатих, Стамбул, Турция) .
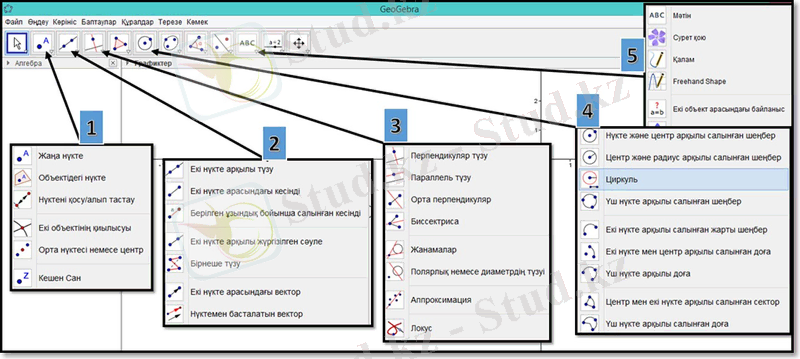
1-сурет. Geogebra ИМО-да элементар салуларды орындауға қажет құралдар
Жана нүкте енгізуге арналған командалар тобы. Сызбадағы екі обектінің қиылысу нүктелерін, кесіндінің ортасын белгілеуге немесе жана нүкте енгізуге мүмкіндік береді.
Сызғыш аксиомаларын сақтай отырып, сызғыштың мүмкіндіктерін толық пайдалануға мүмкіндік беретін құралдар тобы. Қосымша берілген ұзындық бойынша кесінді салу, екі нүкте арасындағы вектор салуға мүмкіндік береді.
Түзуге перпендикуляр, паралель түзу салу және бұрышқа биссектриса шеңберге жанама жүргізуге мүмкіндік беретін құралдар тобы. Циркуль аксиомасының ерекшеліктерін сақтай отырып, қарапайым циркуль мүмкіндіктерін кеңейтетін құралдар. Үш нүкте арқылы шеңбер салуға, диаметрдің ұштары бойынша жарты шеңбер салуға, доға салуға мүмкіндік береді. Сызбаға қосымша мәтін немесе сурет енгізуге мүмкіндік береді. Сызбадағы әр объектінің атауын, түсін, сызық қалыңдығын, типін, толығымен өзгертуге болады. Ол үшін объектіге тышқанның оң жақ батырмасын басып объект баптаулары командасын таңдау қажет.
Жоғарыда (1-сурет) көрсетілгер құралдарды пайдалана отырып мектеп курсының элементар салу есептерін салайық.
Есептер қарастырайық:
1. және ұштары берілген кесіндінің ортасын салу. Бұл есептің шешуін әр түрлі құралдар көмегімен табамыз.
I Циркуль және сызғыш.
Тізбектей саламыз:
1. түзуін ( 2 негізгі салу) ; (екі нүкте арасындағы кесінді)
2. шеңберін (4 негізгі салу) ; (циркуль)
3. шеңберін; (циркуль)
4. және шеңберлерінің және ортақ нүктелерін ( 6 негізгі салу) ; (екі обьектінің қиылысуы)
5. түзуін (2 негізгі салу) ; (екі нүкте арасындағы кесінді)
6. және түзулерінің ортақ нүктесін; (екі обьектінің қиылысуы)
, яғни ізделінді нүкте екеніне оңай көз жеткізуге болады.

1-сызба. Кесіндіні қақ бөлу
II. Циркуль.
Тізбектей саламыз:
1. шеңберін (аксиома Б, а) ; (нүкте және центр арқылы салынған шеңбер)
2. шеңберін; (нүкте және центр арқылы салынған шеңбер)
3. және шеңберлерінің ортақ нүктесін (6, 7 аксиома) ; (екі объектінің қиылысуы)
4. ; шеңберін; (нүкте және центр арқылы салынған шеңбер)
5. және шеңберлерінің, нүктесінен басқа, D ортақ нүктесін; (екі объектінің қиылысуы)
6.
 шеңберін; (нүкте және центр арқылы салынған шеңбер)
шеңберін; (нүкте және центр арқылы салынған шеңбер)
7. және шеңберлерінің нүктесінен басқа, ортақ нүктесін; (екі объектінің қиылысуы) және бір түзде орналасқанын ескерсек және де . Әрі қарай саламыз. ;
8. шеңберін; (нүкте және центр арқылы салынған шеңбер)
9. және шеңберлерінің және ортақ нүктелерін; (екі объектінің қиылысуы)
10. шеңберін; (нүкте және центр арқылы салынған шеңбер)
11. шеңберін; (нүкте және центр арқылы салынған шеңбер)
12. және шеңберлерінің, нүктесінен басқа, ортақ нүктесін; (екі объектінің қиылысуы)
нүктесі кесіндісінде орналасқанын көруге болады. Сонымен бірге,
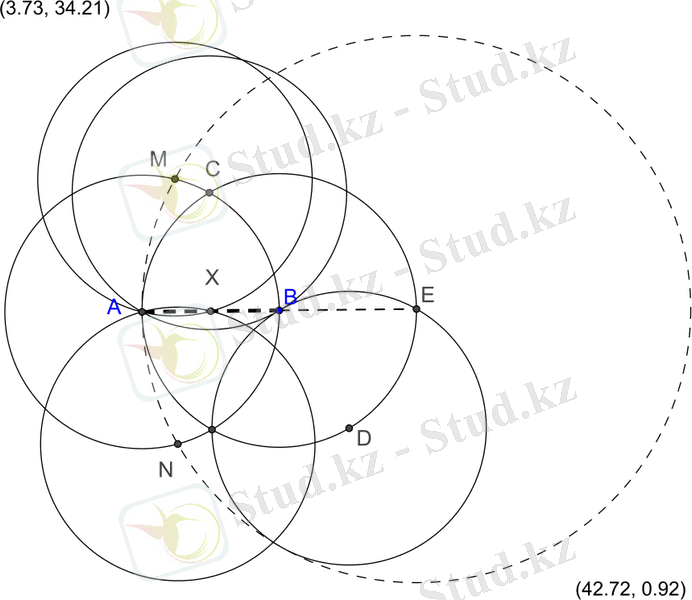
2-сызба. Кесіндіні қақ бөлу
III. Екі жақты сызғыш.
Тізбектей саламыз:
1. түзуін ( аксиома В, а) ; (екі нүкте арқылы өтетін түзу)
2. -ға параллель және одан қашықтықта өтетін түзуін ( -сызғыш ені) ; (паралель түзу)
3. -ға параллель және одан қашықтықта өтетін, түзуінен басқа, түзуін; (паралель түзу)
4. түзуінде нүктесін ( 7 аксиома) ; (жаңа нүкте)
5. және түзулерін; (екі нүкте арқылы өтетін түзу)
6. және нүктелерін ( 6, 7 аксиома) ; (екі объектінің қиылысуы)
( жазуы, және түзулерінің қиылысу нүктесі екенін білдіреді)
7. және түзулерін; (екі нүкте арқылы өтетін түзу)
8. ; (екі объектінің қиылысуы)
9. түзуін; (екі нүкте арқылы өтетін түзу)
10.
- үшбұрышының орта сызығы болғандықтан, және - оның медианалары, ал бұдан, - медиана, демек - ізделінді нүкте.
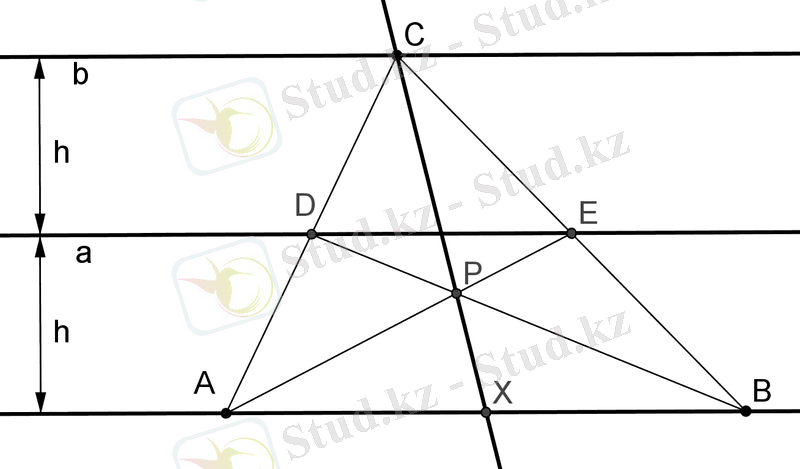
3-сызба. Кесіндіні қақ бөлу
IV. Тік бұрыш.
Тізбектей саламыз:
1. түзуін саламыз ( аксиома Г, а) ; (перпендикуляр түзу)
2. түзуіне перпендикуляр a және b түзулерін жүргіземіз (аксиома Г, ә) ;
3. a түзуінде, нүктесінен басқа өз еркімізше нүктесін аламыз (4, 7аксиома) ; (екі объектінің қиылысуы)
4. нүктесі арқылы түзуіне түзуінде c перпендикулярын жүргіземіз. Әрі қарай тізбектей саламыз: (перпендикуляр түзу)
5.
6. және түзулерін; (перпендикуляр түзу)
7. нүктесін; (екі объектінің қиылысуы)
8. түзуіне перпендикуляр түзуін; (перпендикуляр түзу)
9.
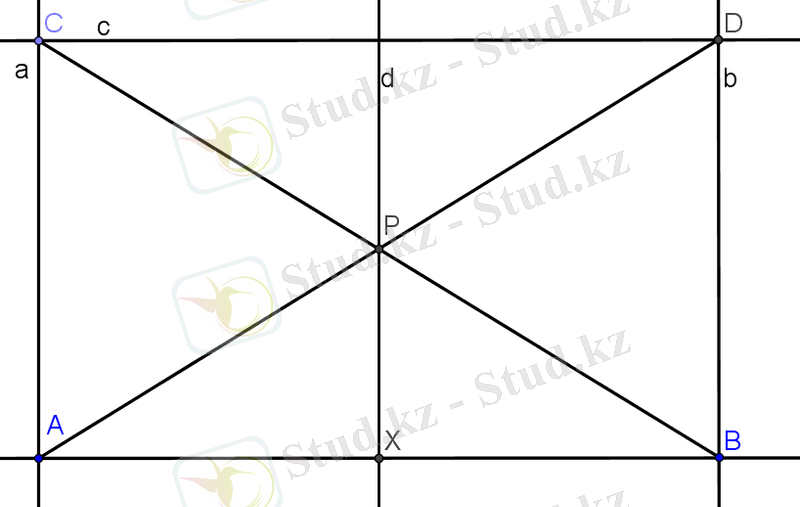
4-сызба. Кесіндіні қақ бөлу
2. Берілген бұрыштың биссектрисасын салу.
бұрышын саламыз.
Тізбектей саламыз:
1) шеңберін (аксиома Б, а) ;
2) және ортақ нүктелерін (6 негізгі салу) ;
3) шеңберін;
4) шеңберін;
5) және шеңберлерінің ортақ нүктесін;
6) түзуін (2 негізгі салу) ;
сәулесі - берілген бұрыш биссектрисасы.
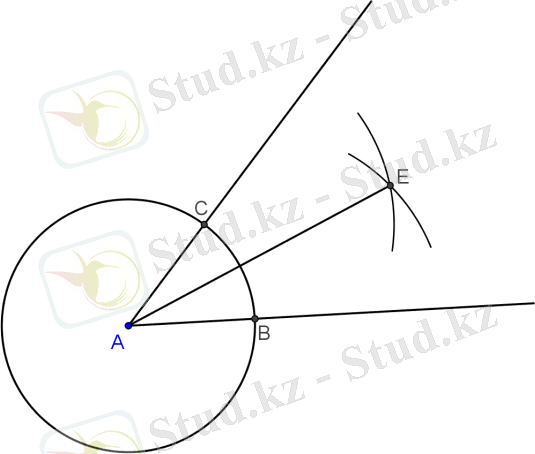
5-сызба. Биссектриса
Дәлелдейік:
және үшбұрыштарын қарастырайық:
, өйткені
1) - ортақ қабырға;
2) - шеңбер радиустары;
3) (салу бойынша) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz