Үздіксіз бөлшектер арқылы анықталмаған теңдеулерді шешу әдістері


№ 11 мектеп-лицейі
Авторы: Әлібекова Айжан
11 сынып оқушысы
Тақырыбы: Анықталмаған теңдеулерді шешудің кейбір әдістері
Секция: Математика
Ғылыми жетекшісі: Қорқыт Ата атындағы Қызылорда
Университетінің «Физика және математика» кофедрасының
қауымдастырылған профессоры, педагогика ғылымдарының
кандидаты Меңліқожаева Саулеш Қойлыбайқызы
Жетекшісі: Джузбаева Айнур Мнажқызы
№ 11 мектеп-лицейінің математика пәнінің
мұғалімі
2021-2022 оқу жылы
АННОТАЦИЯ
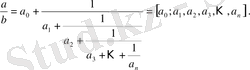
Зерттеу жұмысында қарастырылатын үздіксіз бөлшектер кез келген алдын ала берілген дәлдікпен рационал бөлшектер арқылы өрнектеуге мүмкіндік тудырады, бұл жағынан алғанда үздіксіз бөлшектердің маңызы ондық бөлшектердікінен кем түспейді.
Үздіксіз бөлшектердің таза практикалық қолданылуымен қатар теориялық маңызы да зор. Олардың әдістері негізінен алғанда сандар теориясында, алгебрада, ықтималдықтар теориясында тіпті анализде де қолданылады.
AnnotationContinued fractions, considered in the research work, allow expressing in terms of rational fractions with any predetermined accuracy; in this sense, the value of continued fractions is not inferior to decimal ones.
Along with the purely practical use of continued fractions, it is of great theoretical importance. Their methods are mainly used in number theory, algebra, probability theory and even analysis.
АННОТАЦИЯ
Непрерывные дроби, рассматриваемые в исследовательской работе, позволяют выражать через рациональные дроби с любой заранее заданной точностью, в этом смысле значение непрерывных дробей не уступает десятичным.
Наряду с чисто практическим использованием непрерывных дробей имеет большое теоретическое значение. Их методы в основном используются в теории чисел, алгебре, теории вероятностей и даже в анализе.
МАЗМҰНЫ
КІРІСПЕ
Сандар теориясы курсында үздіксіз бөлшектер теориясының маңызы зор. Басқа әдістер арқылы мұндай шешімдердің бар екені дәлелденіп жатқан кезде үздіксіз бөлшектерді қолдана отырып есептердің дәл шешімдерін беруге болады.
Үздіксіз бөлшектердің таза практикалық қолданылуымен қатар теориялық маңызы да зор. Олардың әдістері негізінен алғанда сандар теориясында, алгебрада, ықтималдықтар теориясында, тіпті, анализ бен механикада да қолданылады.
Үздіксіз бөлшектер жайлы біраз деректерге тоқталатын болсам, үздіксіз бөлшектер туралы деректер ХVІ ғасырдағы итальян математигі Р. Бомбеллидің еңбектерінде кездеседі. Оны ХVІІ ғасырда ағылшын математигі Дж. Валлис зерттеген. Үздіксіз бөлшектердің кейбір маңызды қасиеттерін Х. Гюйгенс ашқан. Сонымен қатар ХVІІІ ғасырда үздіксіз бөлшектер теориясының дамуына Л. Эйлер өзінің үлкен үлесін қосты. Ал П. Л. Марков пен А. А. Чебышев ХІХ ғасырда үздіксіз бөлшектерді ортогональ көпмүшеліктерді зерттеу үшін қолданды.
Сонымен қатар сандар теориясы пәнінің дамуында ұлы француз математигі Жозе Луи Лагранж, Эварист Галуа еңбектерінің мәні зор. Сандар теориясында Лагранж шектеусіз үздіксіз бөлшектер теориясының негізгі теорияларын берді және олардың анықталмаған теңдеулерді шешуге қолданылуын көрсетті. Сонымен қатар Лагранждың сандар теориясынан зерттеулері, нақты сандардың арифметикалық қасиеттерін оқып-білуде үздіксіз бөлшектердің негізгі рөл атқаратындығын көрсетті.
Э. Галуа теоремасының дәлелдеуі 1828 жылы жарыққа шықты. Сонымен қатар Галуа таза периодты жіктелуде түйіндес квадрат иррационалдықтың дәл сондай элементтері болады, бірақ ол элементтер кері тәртіппен орналасатынын дәлелдеді.
Бұл ғылыми жұмыста шектеусіз үздіксіз бөлшектердің практикалық маңызын, яғни қолданылу жақтарын ашып көрсеттім. Мұнда шектеусіз үздіксіз бөлшектерді қолданып анықталмаған теңдеулерді шешуге болатынын, яғни шектеусіз үздіксіз бөлшектердің қолданылу аймағы өте кең екенін көрсеттім.
«Үздіксіз бөлшектер» атты таныстыру буклетін жасадық.
Зерттеу тақырыбы: Анықталмаған теңдеулерді шешудің кейбір әдістері
Мақсаты: «Анықталмаған теңдеулерді шешудің кейбір әдістері» тақырыбы бойынша теориялық және практикалық материалдарды жалпылау.
Міндеттері:
- Оқушыларды өздерінің практикалық жұмыстарында есептеу әдістерін қолдана білуге үйрету;
- б) Оқушылардың жалпы математикалық білім деңгейін жетілдіру, пән бойынша жүйелі білімді қалыптастыру;
- в) Математикалық есептерді зерттеуде, талдауда болашақ мамандардың шығармашылық ойлау деңгейін дамыту;
- Г) Оқушыларды оқу және ғылыми әдебиеттермен өздігімен жұмыс жасауға үйрету.
Зерттеу әдістері: әдебиет көздерімен жұмыс, ғаламтордан мәлімет іздестіру, жетекшімен әңгімелесу.
Зерттеу нысаны: Анықталмаған теңдеулер.
Болжам: Үздіксіз бөлшектердің қолданыс аясы кең.
2. 1 Анықтамалар, шектеулі және шектеусіз үздіксіз бөлшектер.
Үздіксіз бөлшектер кез келген заттық санды кез келген алдын ала берілген дәлдікпен рационал бөлшектер арқылы өрнектеуге мүмкіндік тудырады, бұл жағынан алғанда үздіксіз бөлшектердің маңызы ондық бөлшектердікінен кем түспейді.
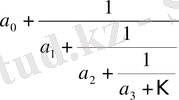 (1)
(1)
түріндегі өрнекті үздіксіз бөлшек деп атаймыз. Мұндағы
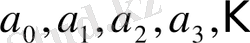 сандар,
сандар,
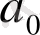 -ден басқасы, бүтін оң сандар. Олар үздіксіз бөлшектің толымсыз бөлінділері деп аталады. Шектеулі толымсыз
-ден басқасы, бүтін оң сандар. Олар үздіксіз бөлшектің толымсыз бөлінділері деп аталады. Шектеулі толымсыз
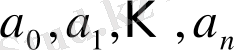 бөлінділері бар үздіксіз бөлшекті шектеулі, ал шектеусіз толымсыз
бөлінділері бар үздіксіз бөлшекті шектеулі, ал шектеусіз толымсыз
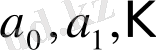 бөлінділері бар үздіксіз бөлшекті - шектеусіз үздіксіз бөлшек деп атайды. Егерде толымсыз бөлінділердің мәндері мен орналасу реті берілсе, онда үздіксіз бөлшек толық анықталған деп саналады. Сондықтан
бөлінділері бар үздіксіз бөлшекті - шектеусіз үздіксіз бөлшек деп атайды. Егерде толымсыз бөлінділердің мәндері мен орналасу реті берілсе, онда үздіксіз бөлшек толық анықталған деп саналады. Сондықтан
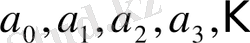 толымсыз бөлінділі үздіксіз бөлшекті
толымсыз бөлінділі үздіксіз бөлшекті
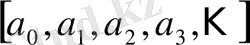 деп те белгілейді. Олай болса,
деп те белгілейді. Олай болса,
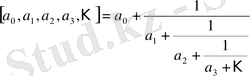
Теорема. Кез келген рационал санды шектеулі, ал иррационал санды шектеусіз үздіксіз бөлшек түрінде көрсетуге болады.
Дәлелдеуі. Шынында да, айталық
 рационал сан болсын,
рационал сан болсын,
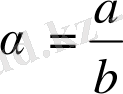 .
.
 -ны
-ны
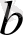 -ге бөліп,
-ге бөліп,
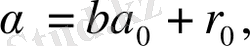 0<
0<
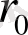 <
<
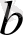 , (2)
, (2)
екенін табамыз. Мұндағы
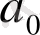 саны
саны
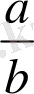 -ден аспайтын ең үлкен бүтін сан, яғни
-ден аспайтын ең үлкен бүтін сан, яғни
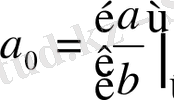 екені түсінікті.
екені түсінікті.
(2) теңдікті
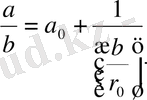 (3)
(3)
түрінде қайта жазып,
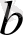 -ні
-ні
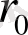 -ге бөлеміз:
-ге бөлеміз:
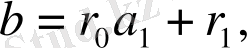
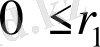 <
<
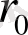 , (4)
, (4)
мұндағы
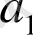 саны
саны
 -ден аспайтын ең үлкен бүтін сан болады, яғни
-ден аспайтын ең үлкен бүтін сан болады, яғни
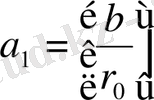 .
.
(4) -ден
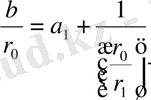 мәнін тауып, (3) -ге қоямыз. Сонда
мәнін тауып, (3) -ге қоямыз. Сонда
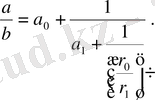 (5)
(5)
Енді
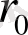 -ді
-ді
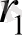 -ге бөлеміз:
-ге бөлеміз:
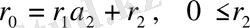 <
<
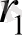 ,
,
мұндағы
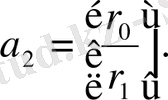 Бұдан
Бұдан
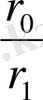 -нің мәнін
-нің мәнін
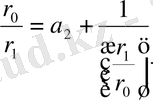
тауып, (5) -ге қойсақ, мынау шығады:
 (6)
(6)
Тағыда
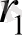 -ді
-ді
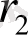 -ге бөлеміз:
-ге бөлеміз:
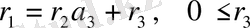 <
<
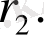
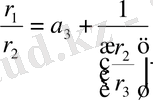 -нің мәнін (6) -ға қойып,
-нің мәнін (6) -ға қойып,
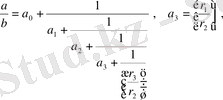 (7)
(7)
аламыз.
Бұдан әрі
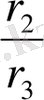 қатынасын тауып,
қатынасын тауып,
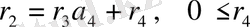 <
<
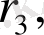
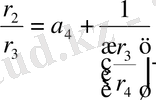
жоғарыдағы сияқты, (7) -ге қоямыз және осы процесті соза береміз. Мына
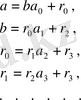
теңдіктері мен
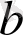 >
>
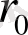 >
>
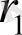 >
>
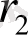 >
>
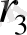 >
>
 теңсіздіктері саны шектеулі бөлулерден кейін, міндетті түрде алдыңғысы соңғысына қалдықсыз бөлінетін
теңсіздіктері саны шектеулі бөлулерден кейін, міндетті түрде алдыңғысы соңғысына қалдықсыз бөлінетін
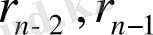 қалдықтары шығатынын көрсетеді:
қалдықтары шығатынын көрсетеді:
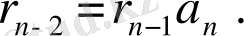
Олай болса,
 рационал санын көрсететін үздіксіз бөлшек саны шектеулі
рационал санын көрсететін үздіксіз бөлшек саны шектеулі
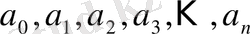 толымсыз бөлінділерін ғана қамтиды, яғни
толымсыз бөлінділерін ғана қамтиды, яғни
Айталық енді,
 - иррационал сан болсын.
- иррационал сан болсын.
 арқылы
арқылы
 -дан аспайтын ең үлкен бүтін санды белгілейік, яғни
-дан аспайтын ең үлкен бүтін санды белгілейік, яғни
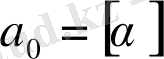 . Сонда
. Сонда
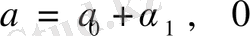 <
<
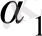 <
<
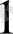 . (8)
. (8)
Мұнда
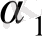 иррационал сан болады, әйтпесе
иррационал сан болады, әйтпесе
 рационал сан болған болар еді.
рационал сан болған болар еді.
Айталық
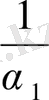 -нің бүтін бөлігі
-нің бүтін бөлігі
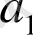 болсын, сонда
болсын, сонда
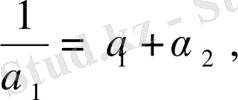 мұнда
мұнда
 <
<
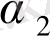 <
<
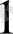 . (9)
. (9)
Дәл осы сияқты, егерде
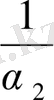 -нің бүтін бөлігі
-нің бүтін бөлігі
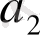 болса, онда
болса, онда
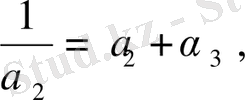
 <
<
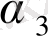 <
<
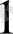 . (10)
. (10)
Жоғарыдағыдай, төмендегі теңдіктерді табамыз:
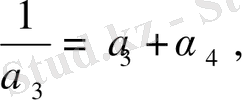
 <
<
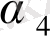 <
<
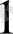 ,
,
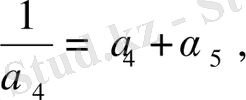
 <
<
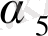 <
<
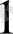 , (11)
, (11)
. . .
Мұндағы
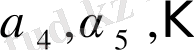 иррационал сандар
иррационал сандар
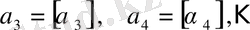
 иррационал сан болғандықтан, сандардың бүтін бөлігін табу процесі шектеулі бола алмайды.
иррационал сан болғандықтан, сандардың бүтін бөлігін табу процесі шектеулі бола алмайды.
(8), (9), (10) және (11) теңдіктерінен біртіндеп,
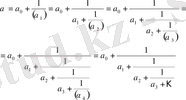
табамыз.
Сөйтіп,
 үшін шектеусіз үздіксіз бөлшек аламыз [8, 272-274б] .
үшін шектеусіз үздіксіз бөлшек аламыз [8, 272-274б] .
 иррационал санын үздіксіз бөлшекке жіктеуге мысалдар қарастырайық.
иррационал санын үздіксіз бөлшекке жіктеуге мысалдар қарастырайық.
Мысал 1.
 -дің жіктелуін табайық.
-дің жіктелуін табайық.
Шешуі.
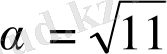 болсын.
болсын.
 -дің бүтін бөлігін айырып алайық
-дің бүтін бөлігін айырып алайық
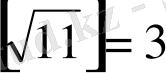 , ал оның бөлшек бөлігін
, ал оның бөлшек бөлігін
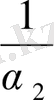 түрінде алайық, мұндағы
түрінде алайық, мұндағы
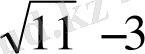 <
<
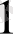 . Сонда
. Сонда
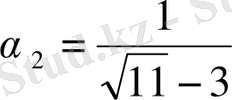 >
>
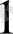 . Осы процесті жалғастыра отырып мынаны аламыз.
. Осы процесті жалғастыра отырып мынаны аламыз.
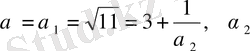 >
>
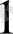 ,
,
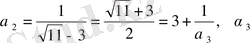 >
>
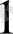 ,
,
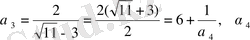 >
>
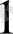 .
.
Егер осы қадамда тоқтайтын болсақ,
 санын былай жазуға болады:
санын былай жазуға болады:
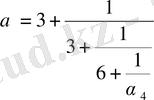
Екінші жағынан
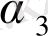 үшін жазылған формуладан
үшін жазылған формуладан
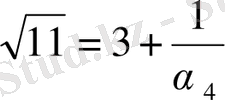 екенін көруге болады. Сондықтан
екенін көруге болады. Сондықтан
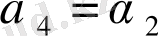 болғандықтан, осы кезден бастап толымсыз бөлінділер қайталанып отырады.
болғандықтан, осы кезден бастап толымсыз бөлінділер қайталанып отырады.
Ендеше
 санының үздіксіз бөлшекке жіктелуі
санының үздіксіз бөлшекке жіктелуі
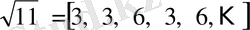
түрінде болады.
Мысал 2.
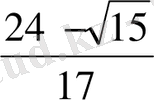 - ті үздіксіз бөлшек түрінде көрсетейік.
- ті үздіксіз бөлшек түрінде көрсетейік.
Шешуі.
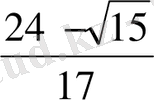 -тің бүтін бөлігі
-тің бүтін бөлігі
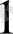 -ге тең, демек
-ге тең, демек


Ары қарай үздіксіз бөлшекке жіктеудегі
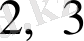 толымсыз бөлінділері шектеусіз қайталанып отырады.
толымсыз бөлінділері шектеусіз қайталанып отырады.
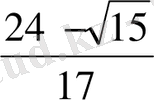 -тің үздіксіз бөлшекке жіктелуі
-тің үздіксіз бөлшекке жіктелуі
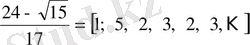
түрінде болады.
Мысал 3.
 жіктелуін табайық.
жіктелуін табайық.
Шешуі.
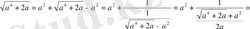
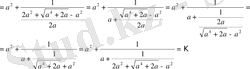
Көріп отырғанымыздай
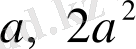 толымсыз бөлінділері қайталанып отыр. Бұл теңдіктер ақырында
толымсыз бөлінділері қайталанып отыр. Бұл теңдіктер ақырында
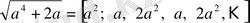
береді.
2. 2 Шектеусіз үздіксіз бөлшектердің лайықты бөлшектері
Шектеулі немесе шектеусіз үздіксіз бөлшек берілсін:
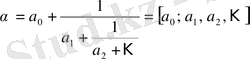 . (1)
. (1)
Бұл үздіксіз бөлшектің алғашқы
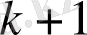 толымсыз бөліндісінен құралған шектеулі үздіксіз
толымсыз бөліндісінен құралған шектеулі үздіксіз
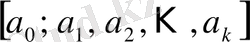 бөлшегін
бөлшегін
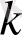 нөмірлі лайықты бөлшек деп атап,
нөмірлі лайықты бөлшек деп атап,
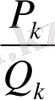 деп белгілейді:
деп белгілейді:
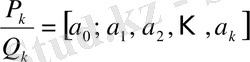 .
.
Дербес жағдайда,
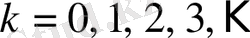 болса,
болса,
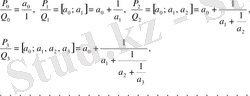
Шектеулі үздіксіз бөлшектің саны шектеулі лайықты бөлшегі, ал шектеусіз
үздіксіз бөлшектің саны шектеусіз лайықты бөлшегі болатыны түсінікті. (1) үздіксіз бөлшек шектеусіз үздіксіз бөлшек болса, оның мәнін төмендегі лайықты бөлшектер шегі ретінде қарастыруға болады:
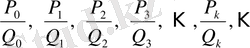
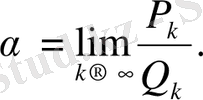
(1) үздіксіз бөлшектің
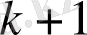 -ден бастап барлық келесі толымсыз бөлінділерінен құралған
-ден бастап барлық келесі толымсыз бөлінділерінен құралған
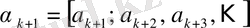
үздіксіз бөлшегін толық бөлінді деп атайды.
(1) үздіксіз бөлшекті
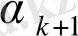 толық бөлінді арқылы шектеулі үздіксіз бөлшек түрінде көрсетуге болады:
толық бөлінді арқылы шектеулі үздіксіз бөлшек түрінде көрсетуге болады:
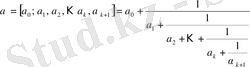
мұндағы
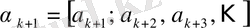 .
.
Егерде
 шектеулі үздіксіз бөлшек болса, онда оның барлық толық бөлінділері де шектеулі үздіксіз бөлшектер болады, ал
шектеулі үздіксіз бөлшек болса, онда оның барлық толық бөлінділері де шектеулі үздіксіз бөлшектер болады, ал
 шектеусіз үздіксіз бөлшек болса, онда толық бөлінділері шектеусіз үздіксіз бөлшектер болады.
шектеусіз үздіксіз бөлшек болса, онда толық бөлінділері шектеусіз үздіксіз бөлшектер болады.
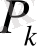 мен
мен
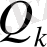 -ның мәндерін кесте бойынша да есептеуге болады.
-ның мәндерін кесте бойынша да есептеуге болады.
Кесте 1. 1 Лайықты бөлшектерді есептеу
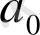
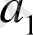
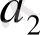
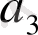

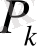
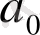
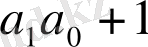
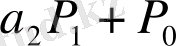
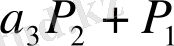

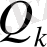
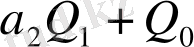
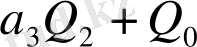

2. 3 Лайықты бөлшектердің қасиеттері
Лайықты бөлшектердің қасиеттеріне тоқталайық.
 Тетелес
Тетелес
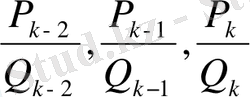 үш лайықты бөлшектің алымдары
үш лайықты бөлшектің алымдары
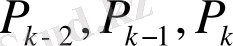 мен бөлімдері
мен бөлімдері
 өзара
өзара
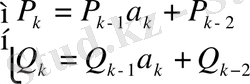 (1)
(1)
қатысы арқылы байланысады.
Дәлелдеуі. Айталық, шектеулі немесе шектеусіз үздіксіз
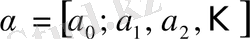
бөлшек берілсін. Егер
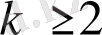 болса,
болса,
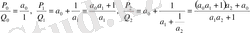 .
.
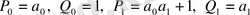 болғандықтан,
болғандықтан,
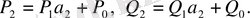 Сөйтіп,
Сөйтіп,
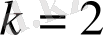 болғанда (1) қатыс орынды болады. Айталық (1) қатыс
болғанда (1) қатыс орынды болады. Айталық (1) қатыс
 болғанда дұрыс болсын
болғанда дұрыс болсын
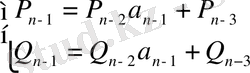 (2)
(2)
Енді (1) қатыстың
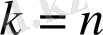 үшін орынды екендігін көрсетейік. Ол үшін
үшін орынды екендігін көрсетейік. Ол үшін
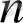 нөмірлі лайықты
нөмірлі лайықты
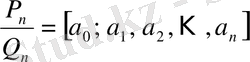
бөлшекті алып,
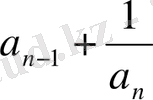 қосындысын
қосындысын
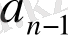 деп белгілейік. Сонда біз
деп белгілейік. Сонда біз
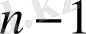 толымсыз бөлінділерден тұратын
толымсыз бөлінділерден тұратын
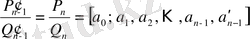 ,
,
үздіксіз бөлшекке келеміз. Бұл бөлшек үшін жоруымыз бойынша төмендегі қатыс орынды:
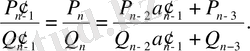
Мұндағы
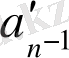 -тың орнына оның мәні
-тың орнына оның мәні
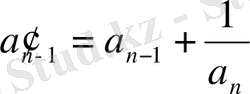
қосындыны қойып,

табамыз, немесе (2) теңдікті алсақ,
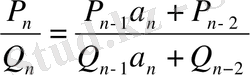 ,
,
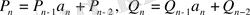
шығады.
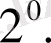 Егерде
Егерде
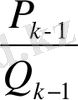 мен
мен
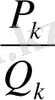 кез келген тетелес тұрған екі лайықты бөлшек болса, онда
кез келген тетелес тұрған екі лайықты бөлшек болса, онда
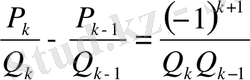
немесе
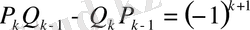 (3)
(3)
қатысы орынды.
Дәлелдеуі. Шынында да,
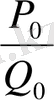 мен
мен
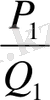 лайықты бөлшектері үшін (3) қатыстың орынды екендігін тікелей тексеру арқылы байқаймыз:
лайықты бөлшектері үшін (3) қатыстың орынды екендігін тікелей тексеру арқылы байқаймыз:
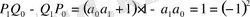 .
.
Айталық,
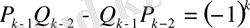 . (4)
. (4)
Онда
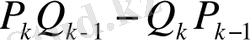 -ге (1) қатыстан
-ге (1) қатыстан
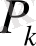 мен
мен
 -нің мәнін тауып алып қойсақ:
-нің мәнін тауып алып қойсақ:

немесе (4) -ге сүйенсек:
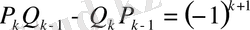
екенін табамыз. (3) қатыстың біріншісі екіншісін
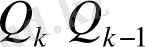 -ге бөлуден шығады.
-ге бөлуден шығады.
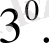 Лайықты бөлшектер - қысқармайтын бөлшектер.
Лайықты бөлшектер - қысқармайтын бөлшектер.
Дәлелдеуі. Шынында, айталық
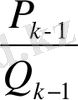 мен
мен
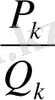 үздіксіз бөлшектің көршілес екі лайықты бөлшектері болсын. Онда
үздіксіз бөлшектің көршілес екі лайықты бөлшектері болсын. Онда
 -
қасиеттегі (3) қатыстың екіншісі бойынша:
-
қасиеттегі (3) қатыстың екіншісі бойынша:
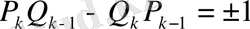 .
.
Бұл қатыстан
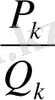 лайықты бөлшегінің алымы
лайықты бөлшегінің алымы
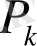 мен бөлімі
мен бөлімі
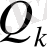 -нің
-нің
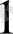 -ден басқа ортақ бөлгіші жоқ екендігі көрініп тұр.
-ден басқа ортақ бөлгіші жоқ екендігі көрініп тұр.
 Барлық
Барлық
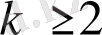 сандары үшін
сандары үшін
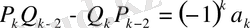
немесе
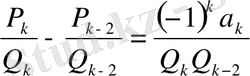 (5)
(5)
қатысы орынды.
Дәлелдеу үшін
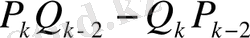 өрнегіне
өрнегіне
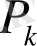 мен
мен
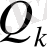 -нің (1) -дегі мәндерін
-нің (1) -дегі мәндерін
қояйық. Сонда

Бұдан (4) -ге сүйенсек:
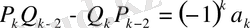 .
.
Мұны
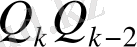 -ге мүшелеп бөлсек, (5) қатыстың екіншісін аламыз.
-ге мүшелеп бөлсек, (5) қатыстың екіншісін аламыз.
Дәлеледенген (5) қатыстан жұп және тақ реті лайықты бөлшектердің өзара орналасуына байланысты маңызды бір салдар шығады.
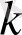 - жұп сан болсын дейік,
- жұп сан болсын дейік,
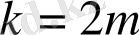 . Онда (5) қатыстан:
. Онда (5) қатыстан:
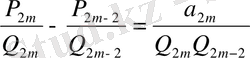 >
>

немесе
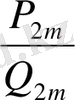 >
>
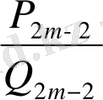
шығады. Мұнда
 дей отырып, индексі жұп болып келген лайықты
дей отырып, индексі жұп болып келген лайықты
бөлшектердің үдеме тізбек құрастыратынын байқаймыз:
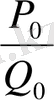 <
<
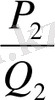 <
<
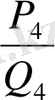 <
<
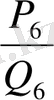 <
<
 (6)
(6)
Егерде
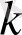 - тақ сан болса,
- тақ сан болса,
 , онда (5) -ден:
, онда (5) -ден:
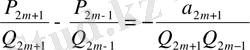 <
<
 ,
,
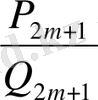 <
<
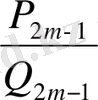 .
.
Мұндағы
 -ге
-ге
 мәндер бере отырып, индекстері тақ сан болып келген лайықты бөлшектер кеміме тізбек құрастырады деген қорытындыға келеміз:
мәндер бере отырып, индекстері тақ сан болып келген лайықты бөлшектер кеміме тізбек құрастырады деген қорытындыға келеміз:
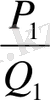 >
>
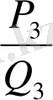 >
>
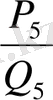 >
>
 (7)
(7)
Егерде (3) -дегі
 десек,
десек,
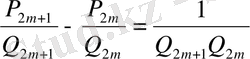 >
>
 ,
,
яғни
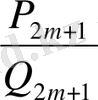 >
>
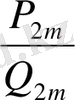
шығады. Сөйтіп, қандай болса да, тақ ретті лайықты бөлшек өзінің алдында тұрған жұп ретті лайықты бөлшектен үлкен болады. Мысалы,
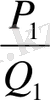 >
>
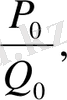
 >
>
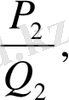
 >
>
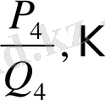 (8)
(8)
(6), (7) және (8) теңсіздіктерден әрбір тақ ретті лайықты бөлшек жұп ретті лайықты бөлшектердің кез келгенінен үлкен болатындығын шығарып алу оңай.
Сөйтіп,
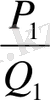 >
>
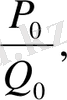
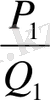 >
>
 >
>
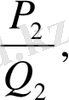
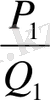 >
>
 >
>
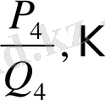
 Жұп ретті лайықты бөлшектер үдеме, ал тақ ретті лайықты бөлшектер
Жұп ретті лайықты бөлшектер үдеме, ал тақ ретті лайықты бөлшектер
кеміме тізбек құрастырады. Әрбір тақ ретті лайықты бөлшек кез келген жұп ретті лайықты бөлшектен үлкен болады.
Дәлелдеуі. Ең алдымен жұп ретті лайықты бөлшектер үдеме, ал тақ ретті
лайықты бөлшектер кеміме тізбек құрастыратынын дәлелдейік.
 - қасиетке
- қасиетке
байланысты
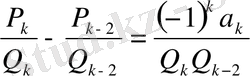 ,
,
сондықтан
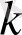 жұп болғанда
жұп болғанда
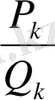 >
>
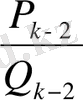 аламыз, ал
аламыз, ал
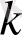 тақ болғанда
тақ болғанда
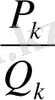 <
<
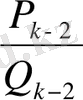 аламыз.
аламыз.
Ендеше тетелес екі
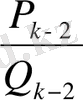 мен
мен
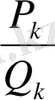 лайықты бөлшектің тақ ретті лайықты бөлшегі жұп ретті лайықты бөлшегінен үлкен.
лайықты бөлшектің тақ ретті лайықты бөлшегі жұп ретті лайықты бөлшегінен үлкен.
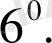 Үздіксіз бөлшек өзінің кез келген тақ ретті лайықты бөлшегінен кем де, жұп ретті лайықты бөлшегінен артық болады.
Үздіксіз бөлшек өзінің кез келген тақ ретті лайықты бөлшегінен кем де, жұп ретті лайықты бөлшегінен артық болады.
Дәлелдеуі. Айталық
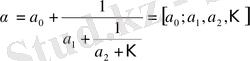
үздіксіз бөлшегі берілсін. Толық бөліндіні
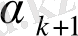 арқылы белгілейік:
арқылы белгілейік:
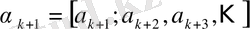 .
.
Сонда
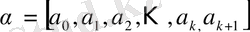 -ні
-ні
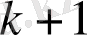 нөмірлі лайықты бөлшек ретінде қарастыруға болады.
нөмірлі лайықты бөлшек ретінде қарастыруға болады.
Демек
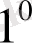 - қасиет бойынша
- қасиет бойынша
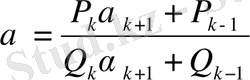 (9)
(9)
Мұндағы
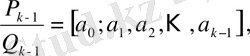
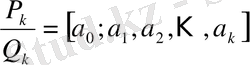
(9) -дан
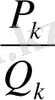 лайықты бөлшегін шегеріп,
лайықты бөлшегін шегеріп,
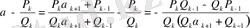
екенін табамыз, немесе (3) -ге сүйенсек
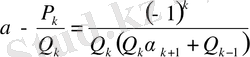 (10)
(10)
шығады.
Егер
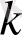 -жұп сан болса,
-жұп сан болса,
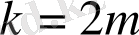 , онда (10) -дан кез келген
, онда (10) -дан кез келген
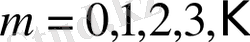 үшін
үшін
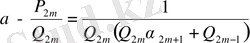 >
>
 (11)
(11)
аламыз, ал
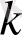 -тақ болса,
-тақ болса,
 , онда
, онда
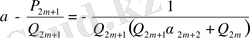 <
<
 (12)
(12)
(11) мен (12) теңсіздіктері
 >
>
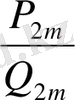 ,
,
 <
<
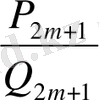 ,
,
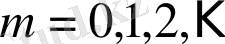
береді, яғни
 үздіксіз бөлшегінің мәні әрбір жұп ретті лайықты бөлшектен артық, бірақ тақ ретті лайықты бөлшектен кем болады.
үздіксіз бөлшегінің мәні әрбір жұп ретті лайықты бөлшектен артық, бірақ тақ ретті лайықты бөлшектен кем болады.
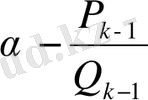 айырмасын табайық. Ол үшін
айырмасын табайық. Ол үшін
 -нің (9) -дағы мәнін пайдаланайық. Сонда
-нің (9) -дағы мәнін пайдаланайық. Сонда
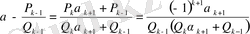 . (13)
. (13)
Егерде
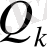 >
>
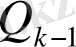 ,
,
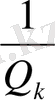 <
<
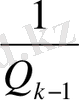 ,
,
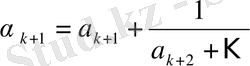 >
>
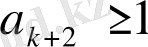 екенін ескерсек, (10) мен (13) теңдіктерінен
екенін ескерсек, (10) мен (13) теңдіктерінен
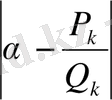 <
<
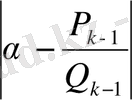 (14)
(14)
теңсіздігіне келеміз. Бұл теңсіздік бізді қажетті қорытындыға әкеледі.
 Үздіксіз бөлшектің мәні әрқашанда кез келген тетелес екі лайықты
Үздіксіз бөлшектің мәні әрқашанда кез келген тетелес екі лайықты
бөлшектің арасында болып, алдыңғысынан қарағанда келесісіне жақын жатады.
Дәлелдеуі. Теорема бойынша
 үздіксіз бөлшегі
үздіксіз бөлшегі
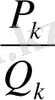 ,
,
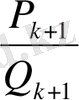 лайықты
лайықты
бөлшектерінің аралығында жатады, сондықтан да
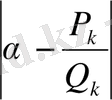 <
<
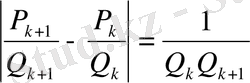 .
.
Бірақ
 >
>
 ,
,
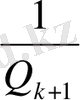 <
<
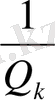
болғандықтан, соңғы теңсіздік
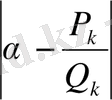 <
<
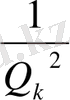
түріне келеді.
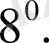 Кез келген
Кез келген
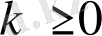 бүтін саны үшін
бүтін саны үшін
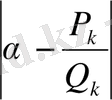 <
<
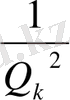 (15)
(15)
теңсіздігі орындалады.
Дәлелдеуі.
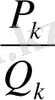 лайықты бөлшегінің алымы мен бөлімі
лайықты бөлшегінің алымы мен бөлімі
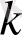 -нің өсуіне байланысты өседі. Сонымен қатар, егер
-нің өсуіне байланысты өседі. Сонымен қатар, егер
 - шектеусіз үздіксіз бөлшек болса, онда
- шектеусіз үздіксіз бөлшек болса, онда
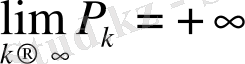 ,
,
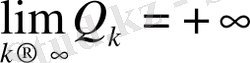
(15) теңсіздікке қарағанда
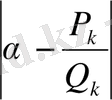 модулы
модулы
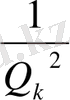 -нен кем бола отырып, қажетінше кішкене бола алатындығы шығады, яғни
-нен кем бола отырып, қажетінше кішкене бола алатындығы шығады, яғни
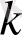 -нің
-нің
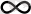 -ке ұмтыла өсуіне байланысты
-ке ұмтыла өсуіне байланысты
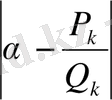 модулы
модулы
 -ге,
-ге,
 -ның
-ның
 -ке ұмтылуына қарағанда тезірек ұмтылады.
-ке ұмтылуына қарағанда тезірек ұмтылады.
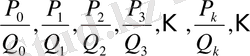 (16)
(16)
лайықты бөлшектердің тізбегі жинақты болса,
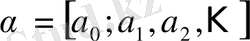 (17)
(17)
шектеусіз үздіксіз бөлшегі жинақты үздіксіз бөлшек деп аталады.
Жоғарыда дәлелденген үздіксіз бөлшектің қасиеттеріне сүйене отырып, натурал мәнді толымсыз
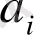 ,
,
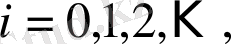 бөлінділі (17) үздіксіз бөлшектің жинақты болатындығын дәлелдеу қиын емес.
бөлінділі (17) үздіксіз бөлшектің жинақты болатындығын дәлелдеу қиын емес.
Шынында, (17) тізбектің бір ғана шекке ұмтылатындығын көрсетейік.
Ол үшін тізбектің жинақтылығы туралы Коши критерийін пайдаланайық.
Бұл критерий төмендегідей.
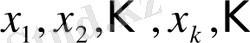 тізбегінің жинақты болуы, демек, шектеулі және бір ғана шекке ұмтылуы үшін, алдын ала берілген оң
тізбегінің жинақты болуы, демек, шектеулі және бір ғана шекке ұмтылуы үшін, алдын ала берілген оң
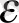 санына сәйкес
санына сәйкес
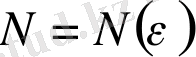 натурал сан (жалпы алғанда
натурал сан (жалпы алғанда
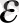 -ға тәуелді) табылып, кез келген бүтін
-ға тәуелді) табылып, кез келген бүтін
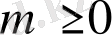 үшін
үшін
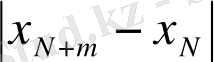 <
<
 (18)
(18)
теңсіздігінің орындалуы қажетті және жеткілікті.
(16) тізбек үшін (18) теңсіздіктің орындалатынын-орындалмайтынын тексерейік:
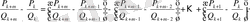
Бұдан
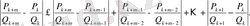 (19)
(19)
Бірақ, бұл арада
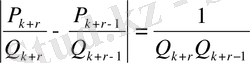 <
<
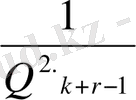
Олай болса (19) теңсіздіктен мынаны табамыз:
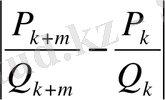 <
<
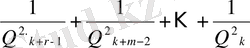 <
<
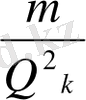 .
.
Егерде
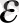 берілсе,
берілсе,
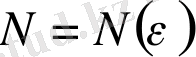 -нің мәні
-нің мәні
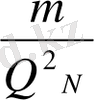 <
<
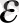 ,
,
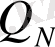 >
>
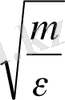 (20)
(20)
теңсіздігінен анықталады.
Қандай да шектеулі
 берілсе де, бөлімі
берілсе де, бөлімі
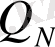 (20) теңсіздікті қанағаттандыратын
(20) теңсіздікті қанағаттандыратын
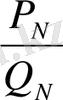 лайықты бөлшек табылады. Сөйтіп, берілген
лайықты бөлшек табылады. Сөйтіп, берілген
 мәніне сәйкес (16) тізбек үшін (18) теңсіздігін қанағаттандыратын
мәніне сәйкес (16) тізбек үшін (18) теңсіздігін қанағаттандыратын
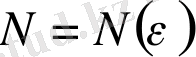 санын әрқашанда тауып алуға болады.
санын әрқашанда тауып алуға болады.
Осымен, (16) тізбектің, олай болса (17) шектеулі үздіксіз бөлшектің жинақтылығы дәлелденді, демек,
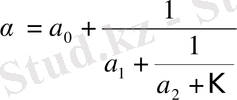
теңдігінің заңдылығы көрсетілді.
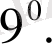 Әрбір
Әрбір
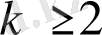 үшін
үшін
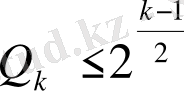
болады.
Дәлелдеуі. Шынында,
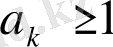 болғандықтан,
болғандықтан,
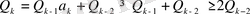 .
.
Дәл осы сияқты:
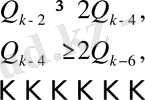
Егер
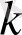 жұп сан болса, онда
жұп сан болса, онда
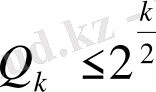 , ал егер
, ал егер
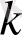 тақ сан болса, онда
тақ сан болса, онда
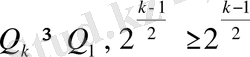 . Бұл теореманың дұрыстығын дәлелдейді.
. Бұл теореманың дұрыстығын дәлелдейді.
 Әрбір
Әрбір
 үшін
үшін
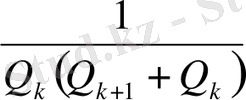 <
<
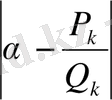 <
<
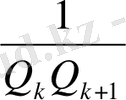 (21)
(21)
теңсіздіктері орындалады.
Дәлелдеуі. Егер
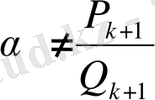 болса, онда біреуі жұп, ал екіншісі тақ болатын
болса, онда біреуі жұп, ал екіншісі тақ болатын
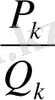 және
және
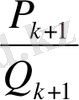 лайықты бөлшектері
лайықты бөлшектері
 -ның әр түрлі жағында жатады, сондықтан
-ның әр түрлі жағында жатады, сондықтан
 -дан олардың әрқайсысына дейінгі ара қашықтық осы екі лайықты бөлшек арқылы пайда болған интервал ұзындығынан кіші болады, яғни
-дан олардың әрқайсысына дейінгі ара қашықтық осы екі лайықты бөлшек арқылы пайда болған интервал ұзындығынан кіші болады, яғни
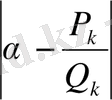 <
<
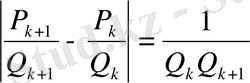 .
.
Егер
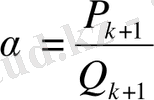 болса, онда
болса, онда
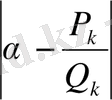
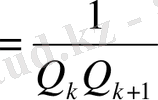 .
.
Енді
 -ның
-ның
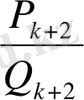 лайықты бөлшегі болсын. Жоғарыда дәлелдегеніміздей
лайықты бөлшегі болсын. Жоғарыда дәлелдегеніміздей
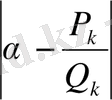 >
>
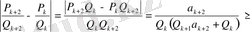
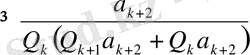
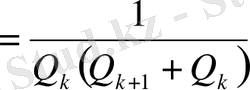 .
.
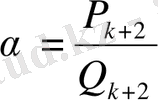 үшін
үшін
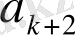 >
>
 болады, сондықтан
болады, сондықтан
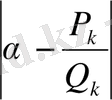 >
>
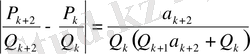 >
>
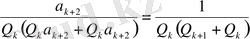 .
.
Егер де
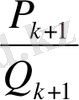 - ең соңғы лайықты бөлшек болса, яғни
- ең соңғы лайықты бөлшек болса, яғни
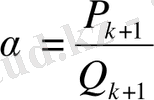 болса, онда
болса, онда
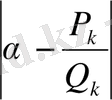
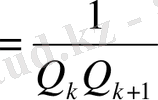 >
>
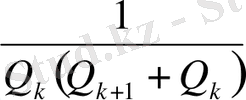 .
.
 (Лагранж теоремасы) . Тетелес екі
(Лагранж теоремасы) . Тетелес екі
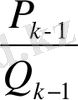 мен
мен
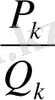 лайықты бөлшектерінің арасында жататын, бөлімі
лайықты бөлшектерінің арасында жататын, бөлімі
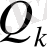 -дан аспайтын
-дан аспайтын
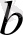 болып келген
болып келген
 оң бөлшегі болмайды.
оң бөлшегі болмайды.
Дәлелдеуі. Айталық,
 бөлшегі
бөлшегі
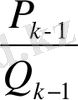 мен
мен
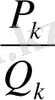 арасында жатып,
арасында жатып,
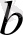 <
<
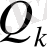 болсын. Онда
болсын. Онда
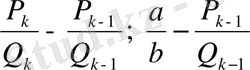
айырмаларының таңбалары бірдей болатындығы түсінікті және
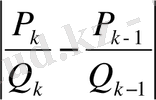 >
>
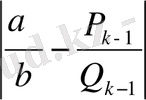
болады.
 - қасиет бойынша
- қасиет бойынша
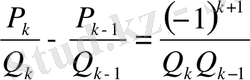
Осыдан
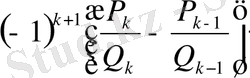 >
>
 ,
,
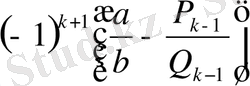 >
>

шығады. Алайда
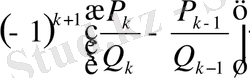 >
>
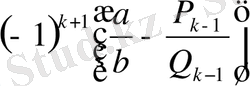
немесе
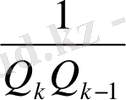 >
>
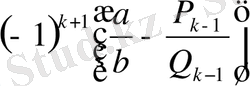
болғандықтан, соңғы теңсіздіктің екі жақ бөлігін де
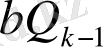 -ге көбейтіп
-ге көбейтіп
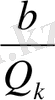 >
>
 >
>

табамыз. Бұл теңсіздіктің оң жақ бөлігі оң және бүтін сан болғандықтан, 1-ден артық болады. Олай болса
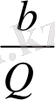 >
>
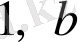 >
>
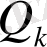 .
.
 (Вален теоремасы) . Тетелес екі лайықты
(Вален теоремасы) . Тетелес екі лайықты
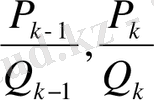 бөлшектерінің ең
бөлшектерінің ең
болмағанда біреуі
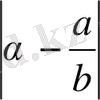 <
<
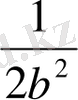
теңдігін қанағаттандырады.
Мұндағы
 саны
саны
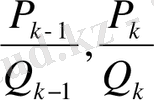 бөлшектерінің бірі.
бөлшектерінің бірі.
Дәлелдеуі. Шынында, айталық
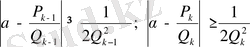
теңсіздіктері қатар орындалсын.
Онда
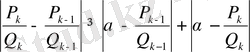
теңсіздігінен
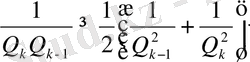
алған болар едік, яғни
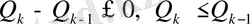 ,
,
бұл
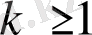 болғанда орындалмайды.
болғанда орындалмайды.
Мысал 1.
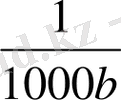 -ға дейінгі дәлдіктегі
-ға дейінгі дәлдіктегі
 -нің
-нің
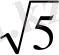 -ке рационал жуықтауын табайық.
-ке рационал жуықтауын табайық.
Шешуі. Бұл есепті шешу үшін, ең алдымен, Дирихле теоремасына сәйкес бөлшектердің арасынан бөлімдері
 -нан кіші болатын бөлшекті табуға болатынын анық көреміз.
-нан кіші болатын бөлшекті табуға болатынын анық көреміз.
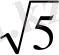 -ті үздіксіз бөлшекке жіктесек
-ті үздіксіз бөлшекке жіктесек
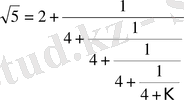 ,
,
яғни
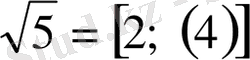 .
.
Лайықты бөлшектерін табайық.
Кесте 1. 2 Лайықты бөлшектер табу

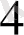
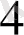
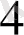
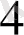
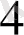

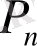

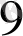
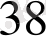
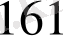
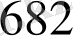


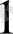
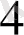


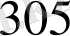
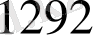

 -нан кіші болатын ең үлкен бөлім
-нан кіші болатын ең үлкен бөлім
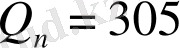 -ке тең екені көрініп тұр. Берілген бөлшек
-ке тең екені көрініп тұр. Берілген бөлшек
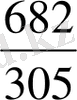 -ке тең; ендеше
-ке тең; ендеше
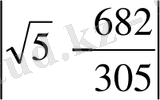 <
<
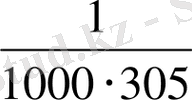 .
.
Мысал 2.
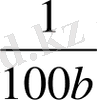 -ға дейінгі дәлдіктегі
-ға дейінгі дәлдіктегі
 -нің
-нің
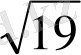 -ға жуықтауын анықтайық.
-ға жуықтауын анықтайық.
Шешуі. Ең алдымен
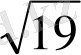 -ті үздіксіз бөлшекке жіктей отырып
-ті үздіксіз бөлшекке жіктей отырып
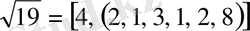
табамыз. Лайықты бөлшектер кестесінен
Кесте 1. 3 Лайықты бөлшектер табу

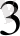
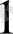

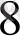

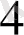
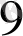
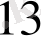
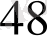
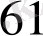
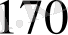


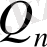

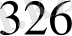

ең үлкен бөлім
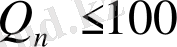 , ол
, ол
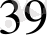 -ға тең екені көрініп тұр. Сондықтан шешім ретінде
-ға тең екені көрініп тұр. Сондықтан шешім ретінде
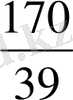 бөлшегін алуға болады;
бөлшегін алуға болады;
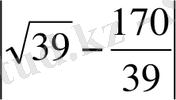 <
<
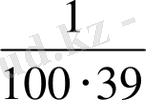 .
.
2. 4 Квадрат иррационалдық және периодты үздіксіз бөлшектер
Рационал сандар бүтін коэффициентті
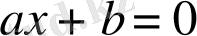 түріндегі бірінші дәрежелі теңдеудің түбірлерін көрсетеді.
түріндегі бірінші дәрежелі теңдеудің түбірлерін көрсетеді.
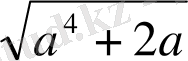
Бүтін коэффициентті квадрат теңдеудің түбірлері болып табылатын иррационалдықтар иррационал сандардың ішіндегі ең қарапайымы болып табылады; мұндай сандарды біз квадраттық иррационалдық деп атайтын боламыз.
 саны квадраттық иррационалдық деп аталады, егер
саны квадраттық иррационалдық деп аталады, егер
 бір уақытта нольге тең емес және бүтін коэффициентті
бір уақытта нольге тең емес және бүтін коэффициентті
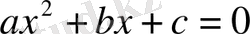 (1)
(1)
теңдеуінің иррационал түбірі болса. Мұндағы
 .
.
(1) теңдеуіндегі
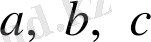 коэффициенттерін өзара жай деп алуға болады; мұндай жағдайда бұл теңдеудің
коэффициенттерін өзара жай деп алуға болады; мұндай жағдайда бұл теңдеудің
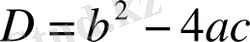 дискриминантын
дискриминантын
 -ның да дискриминанты деп атаймыз.
-ның да дискриминанты деп атаймыз.
(1) теңдеуінің түбірлері
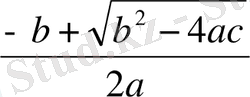 және
және
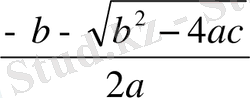 тең, ендеше кез келген
тең, ендеше кез келген
 квадраттық иррационалдығын
квадраттық иррационалдығын
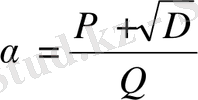 түрінде беруге болады, мұндағы
түрінде беруге болады, мұндағы
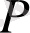 және
және
 бүтін, ал
бүтін, ал
 >
>
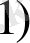 - бүтін квадрат емес сан. (1) теңдеуінің
- бүтін квадрат емес сан. (1) теңдеуінің
екінші түбірін
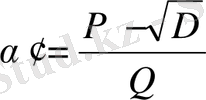
 -мен байланысқан иррационалдық дейміз.
-мен байланысқан иррационалдық дейміз.
Квадрат иррационалдықтың анықтамасында ең алдымен бүтін коэффициентті квадрат теңдеулер жайында айтылып жатқанына көңіл аудару керек. Кез келген
 квадрат теңдеудің, тіпті бірінші дәрежелі, мысалы
квадрат теңдеудің, тіпті бірінші дәрежелі, мысалы
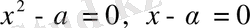 теңдеулерінің түбірі болады.
теңдеулерінің түбірі болады.
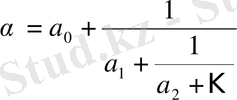
шектеусіз үздіксіз бөлшегінің белгілі
 толымсыз бөлінділер тобы орналасу реттерін сақтай отырып, шектеусіз рет қайталанатын болса, онда мұндай үздіксіз бөлшекті периодты бөлшек деп атайды. Ал орналасу реттерін сақтай отырып қайталанатын толымсыз бөлінділер тобын үздіксіз бөлшектің периоды деп атайды.
толымсыз бөлінділер тобы орналасу реттерін сақтай отырып, шектеусіз рет қайталанатын болса, онда мұндай үздіксіз бөлшекті периодты бөлшек деп атайды. Ал орналасу реттерін сақтай отырып қайталанатын толымсыз бөлінділер тобын үздіксіз бөлшектің периоды деп атайды.
Егер периодтың басы үздіксіз бөлшектің бірінші толымсыз бөліндісімен сәйкес келсе, онда мұндай периодты бөлшекті таза периодты бөлшек деп, ал басқаша жағдайда - аралас периодты бөлшек деп атайды.
Таза периодты үздіксіз бөлшек
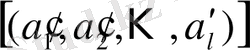 түрінде жазылады,
түрінде жазылады,
ал аралас периодты үздіксіз бөлшек
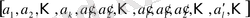
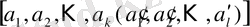 түрінде жазылады.
түрінде жазылады.
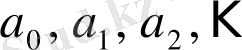 тізбегінің периодының ұзындығын
тізбегінің периодының ұзындығын
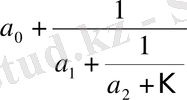
үздіксіз бөлшегінің периодының ұзындығы деп те атаймыз.
Егер
 -ның жіктелуінде
-ның жіктелуінде
 элементтерінен кейін
элементтерінен кейін
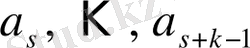 элементтерінің периодты қайталануы басталса, яғни периодтың ұзындығы
элементтерінің периодты қайталануы басталса, яғни периодтың ұзындығы
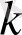 -ға тең болса
-ға тең болса
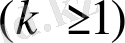 , онда
, онда
 -ны
-ны
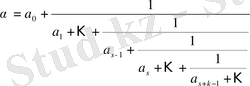
түрінде жазамыз, көбінесе таза периодты жіктелу кезінде, яғни
 болғанда
болғанда
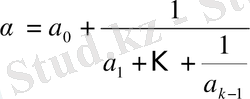
түрінде жазамыз.
Теорема.
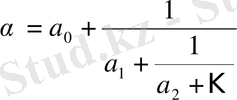 (2)
(2)
үздіксіз бөлшегі периодының ұзындығы
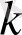 болатын периодты үздіксіз бөлшек болады, сонда және тек қана сонда, егер кейбір
болатын периодты үздіксіз бөлшек болады, сонда және тек қана сонда, егер кейбір
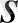 үшін толымсыз бөлінділердің
үшін толымсыз бөлінділердің
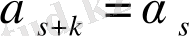 теңдігі орындалса.
теңдігі орындалса.
Дәлелдеуі.
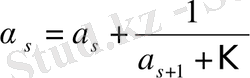 (3)
(3)
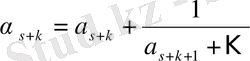 (4)
(4)
1) Егер (2) -нің оң бөлігі периодының ұзындығы
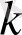 болатын периодты үздіксіз бөлшекті көрсетсе, онда барлық
болатын периодты үздіксіз бөлшекті көрсетсе, онда барлық
 үшін
үшін
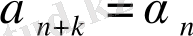 және осы сияқты (3) жіктелуіндегі
және осы сияқты (3) жіктелуіндегі
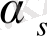 пен (4) жіктелуіндегі
пен (4) жіктелуіндегі
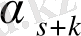 тең, яғни
тең, яғни
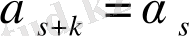 орындалатын қандай да бір
орындалатын қандай да бір
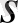 бар болса.
бар болса.
2) Егер
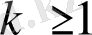 болғанда
болғанда
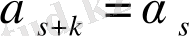 , онда үздіксіз бөлшектің жалғыздығы туралы теоремаға сәйкес (3) және (4) жіктелулері тең, яғни барлық
, онда үздіксіз бөлшектің жалғыздығы туралы теоремаға сәйкес (3) және (4) жіктелулері тең, яғни барлық
 үшін
үшін
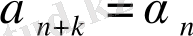 және осыдан (2) ұзындығы
және осыдан (2) ұзындығы
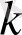 болатын периодты үздіксіз бөлшек болады.
болатын периодты үздіксіз бөлшек болады.
(2) үздіксіз бөлшегі таза периодты болады, сонда және тек қана сонда, егер кейбір
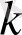 -да
-да
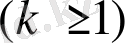
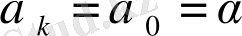 болса.
болса.
Периодты үздіксіз бөлшектердің шамаларын қарастыра отырып, біз
нақты сандардың кейбір бөлігін аламыз. Мұндай сандар жиыны квадрат иррационалдықтар жиынымен сәйкес келеді.
Ең алғаш 1770 жылы Лагранж осындай бір қорытындыға келген.
Кез келген периодты үздіксіз бөлшектің шамасы квадрат иррационалдық болатыны оңай дәлелденеді. Ал кез келген квадрат иррационалдықтың периодты үздіксіз бөлшекке жіктелетіндігін дәлелдеу күрделі; мұны негізінен Лагранж теоремасы деп атайды.
Лагранж теоремасын дәлелдемес бұрын оған көмекші теоремаға тоқтала кетейік.
Теорема. Егер
 квадрат иррационалдығы
квадрат иррационалдығы
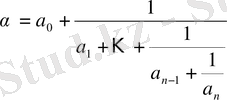 ,
,
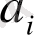 -бүтін
-бүтін
түрінде берілсе, онда
 -дағы сияқты дискриминанты бар
-дағы сияқты дискриминанты бар
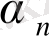 -де квадрат иррационалдық болады.
-де квадрат иррационалдық болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz