Тригонометриялық теңдеулер мен теңсіздіктер: теориядан практикалық шешу тәсілдері


Қазақстан Республикасының Ғылым және Білім министрлігі
Павлодар Педагогикалық Университеті
«Математиканы оқыту әдістемесі» пәні бойынша
Курстық жұмыс
Тақырыбы: Тригонометриялық теңдеулер мен теңсіздіктер және олардың жүйелерін шешу
Мамандық: 6B01510-“Математика”
Орындаған: М-31тобының студенті
Мирзаметова Д. А
Қабылдаған: Алпысов А. К
Павлодар қаласы 2021-2022 оқу жылы
Жоспар:
Кіріспе
- Тригонометрия, теңдеу, теңсіздіктің шығу тарихы
- Негізгі қасиеттері мен формулалары
- Тригонометриялық теңдеулер мен мысалдары
- Тригонометриялық теңдеулерді шешу әдістері.
- Тригонометриялық теңдеулер жүйесін шешу
- Тригонометриялық теңсіздіктер мен мысалдары
- Тригонометриялық функциялардың графигі және қасиеттері.
- Тригонометриялық теңсіздіктердің жүйесін шешу
Қорытынды.
Дереккөздері.
КІРІСПЕ
Қазақстан Республикасы білім және ғылым министрлігінің нұсқалығына сәйкес, егер біз Қазақстан экономикасын, мәдениетін дамытып, жоғары дамыған елдердің қатарына жеткіземіз десек, онда бірінші орында білімді дамытуға тиіспіз. Ол үшін Қазақстанды болашақта өрге жетелейтін білікті мамандар даярлап, Отанына адал қызмет ететін азамат тәрбиелеп шығаруымыз керек. Қазіргі кезде осы мақсаттарды жүзеге асыру үшін жалпы білім беретін орындарға қойылған талаптар қатаңдалып, күннен күнге өсуде. Соның ішінде мектеп курсындағы гуманитарлық пәндер арасында математиканы оқыту үлкен іскерлікті қажет етеді. Мектепте математиканы оқыту - онымен тығыз байланыста жүретін пәндерді меңгеруге, күнделікті тұрмысқа қажетті біліктілік пен дағдыны қалыптастыруға және математиканы тереңдетіп оқытуға тиіс. Математиканы тереңдетіп оқыту - оқушының математикаға тұрақты қызығушылығын тудырып, олардың математикалық қабілеттілігін дер кезінде анықтап, дамуына ықпал етеді де жоғарғы оқу орнына түсуге дайындық мәселелерін шешеді. Оқушылардың математикалық даму әрежесі олардың есеп шығару қабілеттілігінен көрінеді. Кез - келген қиын есепті шығару оқушылардың үлкен еңбекті талап етеді. Мұғалімнің міндеті баланың бойындағы қасиеттерді ояту болып табылады.
Ол үшін мұғалімнің үздіксіз ізденуін, әдістемелік - теориялық білімін жүйелі көтеріп отыруын, терең толғауын, оқушылардың психологиясын зерттеп, тақырып ерекшелігін жете талдай білуін қажет етеді. Әсіресе бұл талаптар жоғары сыныптарда күшейе түседі. Соның ішінде 10 - сыныпта оқытылатын тригонометрия тақырыбының өзі үлкен бір тарау болып келеді. Тригонометриялық функциялар негізгі үш параграфтан тұрады. Соның ішінде біз тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерін шешу әдістерін қарастырамыз. Бұлардың ішіндегі тригонометриялық теңдеулер, теңсіздіктер тақырыбы өте күрделі. Оқушылар тригонометриялық теңдеулер мен теңсіздіктерді шешкенде үлкен қиындықтарға кездеседі. Сол себепті де мен өзімнің курстық жұмысымның тақырыбын Тригонометриялық теңдеулер теңсіздіктер және олардың жүйелерін шешу жолдары деген тақырыпқа арнадым. Курстық жұмысымды жазу барысында мынандай мақсат, міндеттер қойдым.
Мақсаты:
Жалпы тригонометриялық теңдеулердің, теңсіздіктердің түрлерін және олардың шешу жолдарын ашып көрсету.
Міндеті:
- Тригонометриялық теңдеулердің, теңсіздіктердің шешу жолдарын көрсету.
- Тригонометриялық теңдеулерді және теңсіздіктерді шешкенде ыңғайлы әрі оңай жолын таңдауға үйрету.
1. Тригонометрияның шығу тарихы
Тригонометрия (грек. trіgōnon - үшбұрыш және metreo - өлшеу) - геометрияның үшбұрыш элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы өрнектелетін саласы. Тригонометрияның негізгі мәселесі үшбұрыштың белгісіз шамаларын берілген шамалар арқылы есептеу болып табылады. Тригонометрия жазық , түзу сызықты және сфералық тригонометрия болып бөлінеді. Евклидтік кеңістіктің сфералары қарастырылатын тригонометрия сфералық тригонометрия деп аталады. Жазық тригонометрия сфералық тригонометриядан кейінірек дами бастады. Мысалы, Евклидтің «Негіздерінің» 2-кітабында косинустар теоремасы жайында айтылған. Тригонометрияны әл-Баттани (9-10 ғасырлар), Әбу-л-Вефа (10 ғасыр), Бхаскара (10 ғасыр) және ат-Туси (13 ғасыр), т. б. одан әрі дамытты. Оларға синустар теоремасы белгілі болған. Тангенстер теоремасын Региомонтан (15 ғасыр) тапқан. Одан кейін тригонометрияны дамытуға Н. Коперник (16 ғасырдың 1-жартысы), Т. Браге (16 ғасырдың 2-жартысы), Ф. Виет (16 ғасыр), И. Кеплер (16-17 ғасырлар), т. б. үлес қосты. Қазіргі түріндегі Т. Л. Эйлердің еңбектерінде баяндалды. Тригонометрия ғылыми термин ретінде адамның практикалық әрекеттерінің нәтижесінде пайда болды. Ерте кезде астрономия ғылымы, суда жүзу, жер өлшеу, архитектура талаптары қандай да бір элементтер арқылы есептеу әдістерін ойлап табуға әкелді. Мысалы, олардың көмегімен қол жетпейтін заттарға дейінгі қашықтықты анықтау және географиялық карталарды құрастыруға арналған жергілікті жердің геодезиялық көшірмесін жасау жұмыстары бірқатар оңайлатылды. Мектепте тригонометриялық материалмен алғаш рет планиметрия курсын оқығанда танысады. Тригонометрияның көмегімен жазық үшбұрыштарды шығарды. Тригонометриялық қатынастар «синус», «тангенс» деген атқа ие болды, олардың мәндері есептеліп шығарылды. Тригонометриялық танымдардың негізі ежелгі заманда пайда болды. Аталмасы біршама кейінірек шыққанымен, тригонометрияға қатысты қазіргі көптеген ұғымдар мен фактілер бұдан екі мың жыл бұрын белгілі болған. Кейбір тригонометриялық мәліметтер ежелгі вавилондықтар мен египеттіктерге белгілі болған, бірақ ғылым ретінде Ежелгі Грецияда негізделген. Тригонометрия сөзі алғаш рет 1505 жылы неміс геологы және математигі Питискустың кітабының мазмұнында кездеседі. «Тригонометрия» атауының өзі грек сөзінен аударғанда «үшбұрыштарды өлшеу» деген ұғымды білдіреді. Ежелгі грек ғалымы белгілі астроном Клавдий Птолемей (ІІ ғ) «хорда тригонометриясын» ойлап тапты. Дайын кестелермен жұмыс істегенде немесе калькуляторды пайдаланғанда, біз көбінесе кестелер әлі ойлап табылмаған кездердің де болғанын естен шығарып аламыз. Оларды құру үшін аса көлемді есептеулерді орындап қана қоймай, кестелерді құрудың тәсілдерін де ойлап табу қажет болды. Птолемей кестесі бес ондық үлес таңбаларын қоса алғандағы дәлдікпен жасалған. Хордаларды синустармен ауыстырып, тригонометрияның әрі қарай дамуына үндістандық ғалымдар үлкен үлес қосты. Бұл жаңа енгізіу VIII ғасырда тригонометрияны бірте-бірте астрономия тарауынан бөліп алып, жеке ғылымға айналдырды. Ол араб тіліндегі жақын және алыс Батыс мемлекеттерінің математикасына ауысты. Оған үлес қосқандар Аль-хорезми, Аль-Коши, Насриддин Тусси, Жан фурье, Иоганн Бернули, Леонард Эйлер. Л. Эйлер тригонометрияның қазіргі кездегі түріне келтірілген XVIII ғасырдың ірі математигі еді, ол негізі швейцарлық, ұзақ жылдар бойы Россияда жұмыс істеген және Санкт-Петербург ғылым академиясының мүшесі болған. Тригонометриялық функциялардың белгілі анықтамасын да енгізген Л. Эйлер, кез келген бұрыштың функциясын қарастырып, келтіру формулаларын шығарып алды. Осылайша тригонометрия туралы жалпы ұғымдар, тригонометриялық функциялардың белгілеулері және анықтамалары ұзақ тарихи даму процесінде қалыптасып отыр.
Теңдеу деп белгісіз айнымалысы бар алгебралық өрнекті атаймыз. Теңдеулердің түрлері сан алуан- сызықты, квадраттық, тригонометрикалық, логарифмдік және тағы да сол сияқты.
Теңсіздіктерді шешу дегеніміз -теңсіздікті қанағаттандыратын және оған кіретін белгісіздердің мәндер жиынын табу.
Бастапқы кезден тригонометриялық функциялар тік бұрышты үшбұрыштағы қабырғаларының қатынастарымен байланыста болғаны белгілі. Олардың жалғыз аргументі сол үшбұрыштың бір сүйір бұрышы болып табылады.
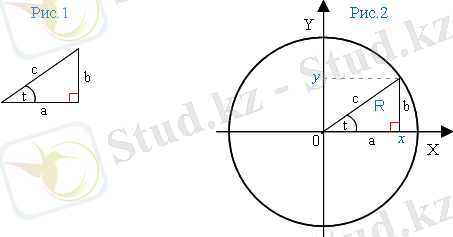
Синус - қарама-қарсы жатқан катеттің гипотенузаға қатынасы.
Косинус - жанама катеттің гипотенузаға қатынасы.
Тангенс - қарама-қарсы жатқан катеттің жанама катетке қатынасы.
Котангенс - жанама катеттің қарама-қарсы жатқан катетке қатынасы
2. Негізгі қасиеттері мен формулалары .
Альфа бұрышының синусы (сәйкесінше, косинус ) деп М0 (1; 0) нүктесін тригонометриялық шеңберде (бірлік шеңберінде) альфа радинаға координаталар басының айналасында айналдырғанда шығатын М нүктесінің ординатасын ( сәйкесінше абциссасын ) атайды.
Бұрыштың тангенсі (катангенсі ) деп бұрыштың синусының(косинусының ) оның косинусына (синусына ) Қатынасын айтады.
Sinx=y, cosx=y, tgx=y, ctgx=y функциялары негізгі тригонометриялық функциялар деп аталады.
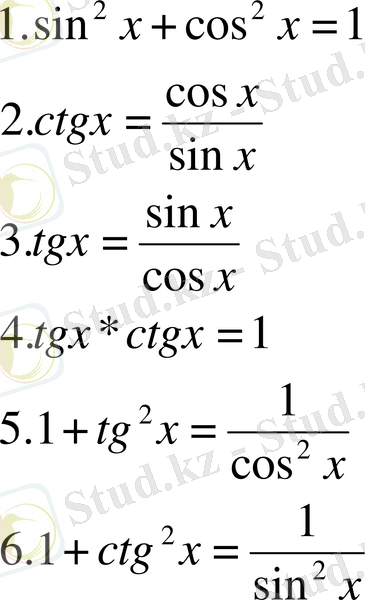
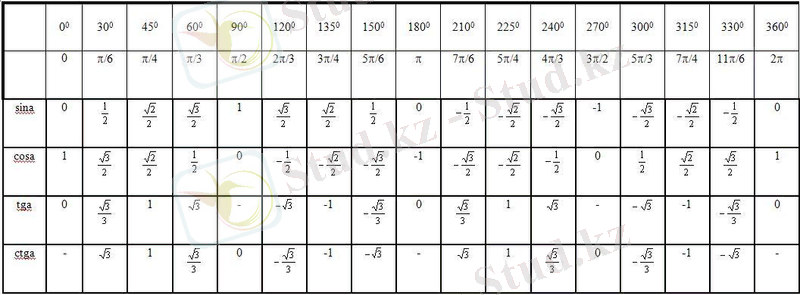
Тригонометриялық функциялардың төмендегі таблицада берілген бұрыштардағы мәндерін жаттап алған жөн.
Синус, тангенс және котангенс функциялары тақ, ал синус функциясы жұп, яғни Х-тің барлық мүмкін мәндері үшін келесі тепе-тең түрлендірулер орындалады:
cos(-α) = cosα - жұп
sin(-α) = - sinα;
tg(-α) =-tg α;
ctg(-α) =-ctg α - тақ
Келтіру формулалары
Келтіру формуласы тригонометриялық функцияның кез-келген аргументін мәндес тригонометриялық функцияның сүйір бұрышына келтіруге мүмкіндік береді.
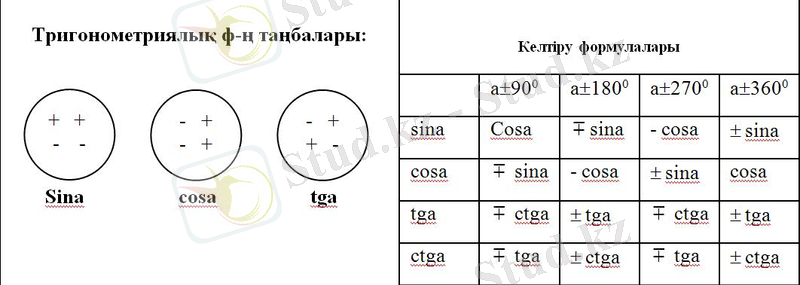
Бұрыштарды қосу және алу формулалары.
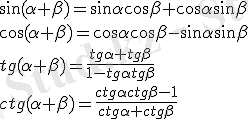
3. Тригонометриялық теңдеулер.
Тригонометриялық теңдеу деп айнымалысы тригонометриялық функция ішінде берілген теңдеуді айтады.
Тригонометриялық теңдеулерді шешудің негізгі ерекшеліктері бар
1) Тригонометриялық теңдеудің бір түбірі болса, онда оның шексіз түбірлері болады.
2) Тригонометриялық теңдеуді оның екі жақ бөлігінде ортақ көбейткіш болатын тригономнтриялық функцияға бөлуге болмайды, себебі теңдеудің ең болмағанда бір шешімі жоғалады.
Қарапайым тригонометриялық теңдеулер.

Тригонометриялық теңдеулерді шешуді негізінен мынадай қарапайым тригонометриялық теңдеулерге келтіріп алып шешеді: sin x = a, cos x = a, tgx = a, ctgx = a . Енді осы теңдеулерді шешу тәсілдерін қарастырайық.
- sinx=a, ∣a∣≤1теңдеуі. Егер ∣a∣∈1 болса, онда бұл теңдеудің екі шешімі бар:α+2κπжәнеβ+2κπ, κ∈ZАлβ=π−αболғандықтан, бұл шешімдерді сәйкесα+ 2κπжәне −α+( 2κ+1 ) πнемесе оларды біріктіріп, (−1 ) κ α+2κπ, κ∈Z, түрінде жазуға болады.
Мұнда α =arcsin a болатынын ескерсек, онда берілген теңдеудің шешімін
x =(−1) κ arcsin a + κπ, κ ∈ Z (1)
түрінде жазамыз. Егер ∣ a ∣=1 немесе ∣ a ∣=0 болса, онда (1)
формуладан төмендегідей дербес жағдайлардағы формулаларды аламыз:
sin x =1 , ⟶ x = +2 κπ, κ ∈ Z;
sin x =0 , ⟶ x = κπ, κ ∈ Z; (2)
sin x =−1 , ⟶ x = +2 κπ, κ ∈ Z;
- cosx=a, ∣a∣≤1 теңдеуі. Оның шешімдері
x =±arccos a +2 κπ, κ ∈ Z (3)
түрінде жазылады. Формуланың дербес жағдайлары ( ∣ a ∣=1 , a =0 ) :
cos x =1 , ⟶ x =2 κπ, κ ∈ Z ; (4)
cos x =0 , ⟶ x = +2 κπ, κ ∈ Z;
cos x =−1 , ⟶ x =( 2 κ +1) π, κ ∈ Z .
- tg=a, a∈(−∞; +∞ ) теңдеуінің шешімдері
x = arctga + κπ, κ ∈ Z
- ctgx=a, a∈(−∞; +∞ ) теңдеуінің шешімде
x = arcctga + κπ, κ ∈ Z
4. Тригонометриялық теңдеулерді шешу әдістері
Тригонометриялық өрнектерден құралған теңдеулерді тригонометриялық теңдеулер деп атайды. Жалпы, тригонометриялық теңдеулерді түрлендірулер арқылы қарапайым тригонометриялық теңдеулерге келтіріп шешеді. Ал тригонометриялық теңдеулерді қарапайым теңдеулерге келтірудің жиі қолданылатын бірнеше әдісі бар. Енді осы әдістерге мысалдар келтіру арқылы тоқталып өтейік. Күрделі тригонометриялық теңдеулерді тригонометриялық өрнектерді түрлендіру, көбейткіштерге жіктеу формулалары арқылы бір немесе бірнеше қарапайым теңдеулерге келтіру арқылы шешімін табуға болады.
1. Квадрат теңдеуге келтіретін теңдеулер .
1-есеп
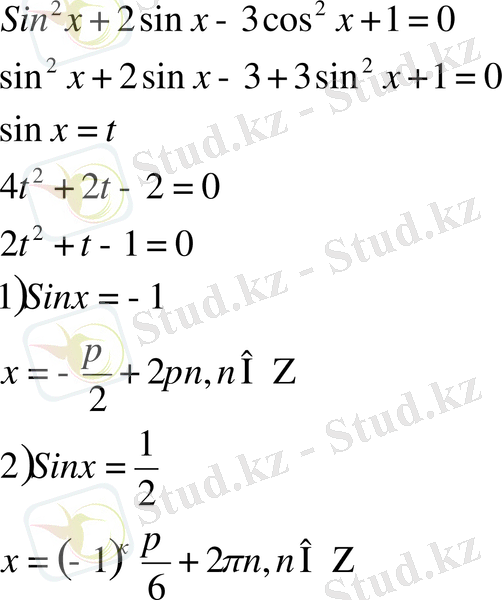
2. Көбейткіштерге жіктеу арқылы.

5. Тригонометриялық теңдеулер жүйесін шешу.
Тригонометриялық теңдеулер жүйесінің шешімі алгебралық теңдеулер жүйесінің шешіміне негізделеді. Тригонометриялық теңдеулер жүйесін шешу үшін алгебралық теңдеулер жүйесін шешу әдістерін білу, түрлендіруде тригонометриялық формулаларды қолдана алу, тригонометриялық теңдеулердің шешімін таба білу қажет.
Тригонометриялық теңдеулер жүйесін шешуге бірнеше мысал қарастырайық.
1 түрі .
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz