Электромагниттік индукция: теориялық негіздер мен сапалық есептерді шешу әдістері


Қазақстан Республикасының білім жӘне ғылым министрлігі
М. Х. Дулати атындағы Тараз өңірлік университеті
Ақпараттық технологиялар, автоматика және телекоммуникация факультеті
Физика
кафедрасы
КУРСТЫҚ Жұмыс
Математикалық физика әдістері
пәні бойынша
Тақырыбы: «Электромагниттік индукция» бөлiмi бойынша сапалық есептерді шешудің ерекшеліктері
Білімгер Турлықұл Гүлназ Тобы В19Физ-1, 3 ___
/аты-жөні/ /қолы/
Жетекші
/қызметі/ /аты-жөні/
Қорғауға жіберілді «»20ж.
/қолы/
Жұмыс қорғалды «»20__ж. бағасы
/жазбаша/
Комиссия мүшелері:
/аты-жөні/ /қолы/
/аты-жөні/ /қолы/
Тараз 2022___
Мазмұны
Кіріспе . . . 3-4
1-бөлім. Теориялық негіз
1. 1 «Электромагниттік индукция заңы» тақырыбына есептер шығару алгоритмі . . . 5-7
1. 2 Электромагниттік индукция . . . 8-11
1. 3 Ленц ережесі . . . 12-16
2-бөлім. Электромагниттік индукция тақырыбына есептер
2. 1 Есептерді шешу әдістері және шығару мысалдары . . . 17-17
2. 2 Дирихле және Нейман есептері . . . 18-20
Қорытынды . . . 21-22
Пайдаланылған әдебиеттер . . . 23
Кіріспе
Математикалық физика қатаң математикалық идеяларды физикадан туындаған мәселелерге қолданады. Сондықтан, бұл өте кең тақырып.
Математика мен физика дәстүрлі түрде тығыз байланысты пәндер болып табылады және Ньютон мен Гаусс сияқты көптеген тарихи тұлғалар физиктер де, математиктер де болған. Дәстүрлі түрде математикалық физика есептеудегі тәсілдермен, әсіресе дифференциалдық теңдеулермен өте тығыз байланысты болды. Алайда соңғы жылдары, ішінара супержол теориясының өсуіне байланысты, математиканың көптеген салалары физикаға негізгі үлес қосты.
Дьюкте зерттелген кейбір математикалық физика геометриялық идеялармен байланысты. Мысалы, Хуберт Брей гравитацияны, қара тесіктерді және кеңістік уақытының қисаюын зерттеу үшін минималды беттер мен гармоникалық функциялар сияқты геометриялық құралдарды пайдаланады. Оны галактикалар массасының көп бөлігін құрайтын қараңғы материя да қызықтырады және оны «ғаламның кең ауқымды түсіндірілмеген қисықтығы» деп атауға болады.
Дифференциалдық геометрия сияқты, алгебралық геометрия пәні қазір математикалық физикада көптеген қолданбаларға ие. Пол Аспинволл - физикалық әлем үшін жолдық теорияларға үміткер жоғары өлшемді кеңістіктерді (және олардың неғұрлым таныс төрт өлшемді кеңістік уақыттарына тығыздалуын) зерттеу үшін алгебралық геометрияны қолданатын жол теоретигі.
Марк Стерн негізгі ядролық күштерді сипаттайтын математикалық модель және геометрия мен топологияның негізгі құралы болып табылатын Ян Миллс теориясын зерттеу үшін геометрия мен ішінара дифференциалдық теңдеулерді пайдаланады.
Математикалық физика тобы статистикалық механиканың, атомдық және молекулалық физиканың, өрістің кванттық теориясының мәселелерімен және жалпы теориялық физиканың математикалық негіздерімен айналысады. Бұған кванттық механика (релятивистік емес те, релятивистік те), атомдық және молекулалық физика, конденсацияланған заттардағы тәртіпсіздік әсерлері, модельдік ферромагнетиктердің фазаларының болуы мен қасиеттері, материяның тұрақтылығы, симметрия теориясы және кванттық симметрияның бұзылуы сияқты пәндер кіреді. Өріс теориясы (жалпы да, нақты модельдерде де) және функционалдық талдаудағы математикалық әзірлемелер, алгебра және осындай пәндер әкелетін заманауи ықтималдықтар теориясы.
Математикалық физикада сіз теориялық физиканы дифференциалдық теңдеулер, векторлық есептеулер және қолданбалы математикадағы жоғары деңгейлі математикалық курстармен біріктіресіз. Сондай-ақ механика, электр тогы және магнетизм, компьютерлік бағдарламалау, оптика және т. б. бойынша тәжірибелік зертханаларда осы оқуды қолдану мүмкіндігіне ие боласыз.
- «Электромагниттік индукция заңы» тақырыбына есептер шығару алгоритмі
«Электромагниттік индукция заңы» тақырыбына есептер шығару алгоритмі
1. Тізбекпен байланысты магнит ағынының өзгеру себептерін анықтаңыз, және В, S мәндерінің қайсысы Ф үшін өрнекке кіретінін анықтаңыз, уақыт өте өзгереді.
2. Электромагниттік индукция заңының формуласын жаз:
3. ΔФ өрнегі кеңейтілген (Ф) түрінде орнына ауыстырылады және электромагниттік индукция заңының бастапқы формуласы қойылады.
4. Барлық көмекші шарттарды математикалық түрде жаз.
5. Алынған теңдеулер жүйесін қажетті мәнге қатысты шешіңіз.
6. Сыни тұрғыдан тексеру және бағалау шешімі.
Электромагниттік индукцияның не екенін түсінбес бұрын, магнит ағыны сияқты затты анықтау керек.
Елестетіп көріңізші, сіз қолыңызға құрсау алып, жаңбырға шықтыңыз. Неғұрлым күшті жаңбыр болса, соғұрлым бұл құрсау арқылы су көп өтеді - су ағыны көбірек болады.
Егер құрсау көлденең болса, онда ол арқылы су көп өтеді. Ал егер сіз оны айналдыра бастасаңыз - қазірдің өзінде аз, өйткені ол тік бұрышта орналаспаған.

Енді құрсауды тігінен қоямыз - одан бір тамшы да өтпейді (әрине, жел соқпаса) .

Магнит ағыны негізінен құрсау арқылы өтетін судың бірдей ағыны болып табылады, тек біз жаңбырды емес, аймақ арқылы өткен магнит өрісінің шамасын қарастырамыз.
Тізбектің S ауданы арқылы өтетін магнит ағыны - бұл магнит индукциясы векторының B модулінің, осы ағынның енетін S бетінің ауданы мен бұрыш косинусының көбейтіндісіне тең скаляр физикалық шама. α магниттік индукция векторының бағыты мен нормаль векторының арасындағы (берілген беттің жазықтығына перпендикуляр) :
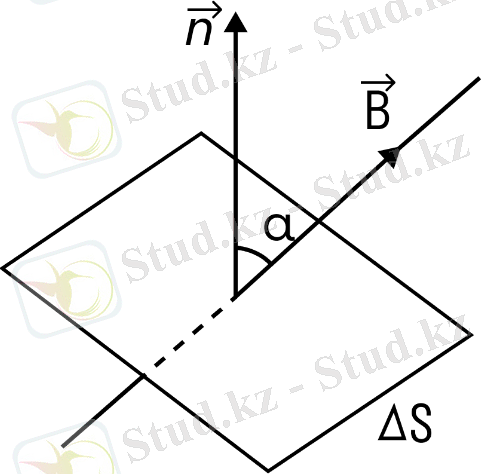
Магниттік ағын
Ф - магнит ағыны [Вб]
B - магниттік индукция [Tл]
S - енетін бетінің ауданы [м²]
Магнит ағынын берілген аумақ арқылы өтетін магниттік сызықтардың санына пропорционалды шама ретінде бейнелеуге болады.
α бұрышына байланысты магнит ағыны оң (α < 90°) немесе теріс (α > 90°) болуы мүмкін. Егер α = 90° болса, онда магнит ағыны 0. Бұл бұрыштың косинусына байланысты.
Магниттік ағынды тізбек аймағын, өріс индукциялық модулін немесе магнит өрісіндегі тізбектің орнын өзгерту (оны айналдыру) арқылы өзгертуге болады.
Біркелкі емес магнит өрісі және жазық емес контур жағдайында магнит ағыны осы бетті бөлуге болатын секциялардың әрқайсысының ауданына енетін магнит ағындарының қосындысы ретінде табылады.
1. 2 Электромагниттік индукция
Электромагниттік индукция - тұйық өткізгіш контурда оған енетін магнит ағыны өзгерген кезде токтың пайда болу құбылысы.
Электромагниттік индукция құбылысын М. Фарадей ашқан.
Майкл Фарадей электромагниттік индукция құбылысын ашуға көмектесетін бірқатар эксперименттер жүргізді.
Тәжірибе уақыты. Бір өткізбейтін негізге екі катушкалар оралған: бірінші орамның бұрылыстары екіншісінің бұрылыстарының арасында орналасқан. Бір катушканың бұрылыстары гальванометрге жабылды, ал екіншісі ток көзіне қосылды.
Кілт жабылып, ток екінші катушка арқылы өткенде, біріншісінде ток импульсі пайда болды. Кілтті ашқан кезде ток импульсі де байқалды, бірақ гальванометр арқылы өтетін ток қарама-қарсы бағытта өтті.
Екінші тәжірибе. Бірінші катушка ток көзіне, екіншісі гальванометрге қосылды. Бұл жағдайда екінші катушка біріншіге қатысты қозғалды. Орамға жақындағанда немесе оны алып тастағанда, ток тіркелді.
Үшінші тәжірибе. Катушка гальванометрге жабық, ал магнит катушкаға қатысты ішке (шыға) жылжиды.
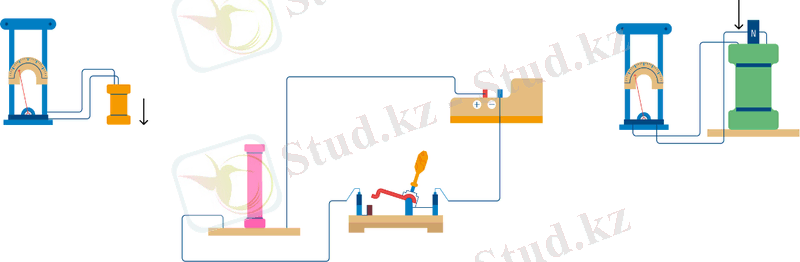
Міне, бұл эксперименттер көрсеткендей:
- Индукциялық ток магниттік индукция сызықтары өзгергенде ғана пайда болады.
- Токтың бағыты сызықтар санының артуымен және олардың азаюымен әртүрлі болады.
- Индуктивті токтың күші магнит ағынының өзгеру жылдамдығына байланысты. Өрістің өзі өзгеруі мүмкін немесе тізбек біркелкі емес магнит өрісінде қозғалуы мүмкін.
Электромагниттік индукция заңы
Электромагниттік индукция заңы (Фарадей заңы) :
Тұйық контурдағы индукциялық ЭҚ контурмен шектелген бет арқылы магнит ағынының өзгеру жылдамдығына таңбасы бойынша тең және қарама-қарсы.
Математикалық түрде оны мына формуламен сипаттауға болады:
- ЭҚК индукциясы [В]
- Магнит ағынының өзгеру жылдамдығы
Формуладағы «-» белгісі индукциялық токтың бағытын ескеруге мүмкіндік береді. Жабық контурдағы индукциялық ток әрқашан тізбекпен шектелген бет арқылы осы ток тудыратын өрістің магнит ағыны индукциялық токтың пайда болуын тудырған өрістегі өзгерістерді азайтатындай етіп бағытталады.
Егер тізбек N бұрылыстан тұрса (яғни ол катушка), онда индукциялық ЭҚК келесідей есептеледі.
- индукцияның ЭҚК [В]
- магнит ағынының өзгеру жылдамдығы [Вб/с]
N - айналымдар саны [-]
Кедергісі R бар тұйық өткізгіш контурдағы индукциялық токтың күші:
Өткізгіш тізбек үшін Ом заңы:
- индукцияның ЭҚК [В]
I - индукциялық ток күші [A]
R - цикл кедергісі [Ом]
Магниттік өрісте қозғалатын өткізгіште индукциялық ЭҚК пайда болуы қозғалыстағы өткізгіштердегі бос зарядтарға Лоренц күшінің әсерімен түсіндіріледі. Лоренц күші бұл жағдайда сыртқы күш рөлін атқарады.
Индукциялық ток өтетін магнит өрісінде қозғалатын өткізгіш магниттік тежеуді бастан кешіреді. Лоренц күшінің жалпы жұмысы нөлге тең.
Тізбектегі жылу мөлшері не өткізгіштің жылдамдығын өзгеріссіз ұстап тұратын сыртқы күштің жұмысы есебінен, не өткізгіштің кинетикалық энергиясының төмендеуіне байланысты бөлінеді.
Жабық контурға енетін магнит ағынының өзгеруі екі себепке байланысты болуы мүмкін:
- контурдың немесе оның бөліктерінің тұрақты магнит өрісіндегі қозғалысына байланысты. Бұл өткізгіштер және олармен бірге бос заряд тасымалдаушылар магнит өрісінде қозғалатын жағдай
- тұрақты контуры бар магнит өрісінің уақытының өзгеруіне байланысты. Бұл жағдайда индукциялық ЭҚК пайда болуын енді Лоренц күшінің әрекетімен түсіндіруге болмайды. Айналадағы магнит өрісі өзгергенде пайда болатын қозғалмайтын өткізгіштердегі электромагниттік индукция құбылысы да Фарадей формуласымен сипатталады.
Осылайша, қозғалатын және қозғалмайтын өткізгіштердегі индукция құбылыстары бірдей жүреді, бірақ индуктивті токтың пайда болуының физикалық себебі осы екі жағдайда әртүрлі болып шығады:
- қозғалатын өткізгіштер жағдайында индукциялық ЭҚК Лоренц күшімен байланысты
- қозғалмайтын өткізгіштер жағдайында индукциялық ЭҚК магнит өрісі өзгерген кезде пайда болатын құйынды электр өрісінің бос зарядтарына әсер ету салдары болып табылады.
Ленц ережесі
Индукциялық токтың бағытын анықтау үшін Ленц ережесін қолдану керек.
Академиялық тұрғыдан бұл ереже келесідей естіледі: магнит ағыны өзгерген кезде тұйық контурда қозғалатын индукциялық ток әрқашан бағытталған, сондықтан ол тудыратын магнит өрісі индукциялық токты тудыратын магнит ағынының өзгеруіне жол бермейді.
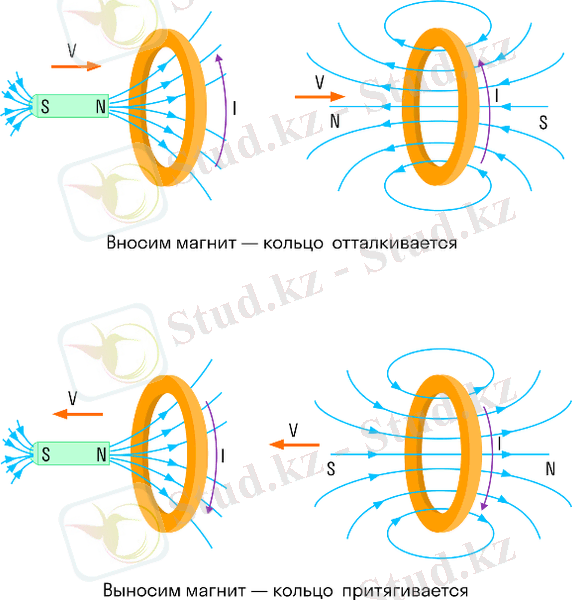
Қарапайым тілмен түсіндіретін болсақ: бұл жағдайда катушкалар - наразы әже. Олар одан магнит ағынын алып қояды - ол оған наразы болады және магнит өрісін жасайды, бұл магнит ағынын қайтарғысы келеді.
Олар оған магнит ағынын береді де ал пайдалан деп айтады, ал әже : «Мен сендердің магнит ағындарыңды не істеймін?» деп осы магнит ағыны сыртқа шығаратын магнит өрісін жасайды.
1. 2
Магниттік индукция B векторының S беті арқылы ағуы беттік интеграл деп аталады:
векторы нормаль n бойымен элементар ауданына бағытталған және оның ауданына тең модулі бар. Белгілерді сәйкестендіру үшін қалыпты вектордың бағыты n және контурды айналып өту бағыты 1-суреттегідей оң жақ бұранданың ою арқылы байланыстырылады деп болжанады.
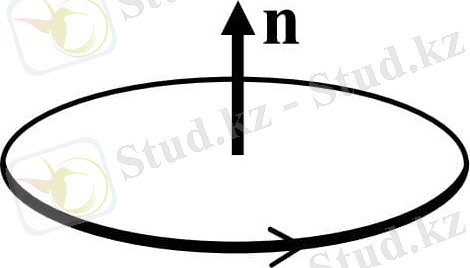
1-сурет. Қалыпты вектордың жазық контурға бағытын анықтау
Магниттік ағынның SI бірлігі вебер (Вб=Т*м 2 ) болып табылады.
Фарадейдің электромагниттік индукция заңы магниттік және электрлік құбылыстардың динамикалық байланысын белгілейді.
Электромагниттік индукция заңының интегралдық түрі: электромагниттік индукцияның ЭҚК ɛ ерікті L тізбегіндегі магнит ағынының Ф еркін S беті арқылы өзгеру жылдамдығына пропорционал, осы контур негізінде:
Минус белгісі өткізгіштердегі индукциялық ЭҚК тудыратын индукциялық ток өзінің магнит өрісімен оны тудырған магнит ағынының өзгеруіне қарсы әрекет ететінін білдіреді (Ленц ережесі) .
Электромагниттік индукцияның ЭҚК пайда болуы электромагниттік өрістегі зарядқа әсер ететін Лоренц күшінің жұмысымен түсіндіріледі.
мұндағы - зарядтың жылдамдығы. Әртүрлі физикалық жағдайларда және әртүрлі анықтамалық жүйелерде бұл күш тек электрлік құрамдас (бірінші мүше) немесе тек магниттік (екінші мүше) болуы мүмкін немесе осы компоненттердің қосындысы болуы мүмкін.
Ф(t) ағынының өзгеруі екі түрлі себеппен туындауы мүмкін, олар бірлесіп әрекет ете алады. Олар келесі екі жағдайға сәйкес келеді:
1) Магниттік индукция векторы В тұрақты, ал Ф(1) өткізгіштердің қозғалысына байланысты өзгереді, мысалы, өткізгіш контурдың деформациясы немесе оның бағытының өзгеруіне қатысты векторының бағыты B.
2) Өткізгіш контур қозғалыссыз, ал Ф(t) шамасының және В(t) бағытының өзгеруіне байланысты өзгереді.
1) жағдайда индукция ЭҚК Лоренц күшінің магниттік құрамдас бөлігі есебінен туындайды, бұл жағдайда өткізгішпен бірге қозғалатын зарядтарға әсер етеді:
Жабық контурда бұл сыртқы күш индукцияның ЭҚК-ін тудырады:
Егер өткізгіштің берілген қимасымен бірге қозғалатын санақ жүйесін алсақ, онда Лоренц күшінің магниттік құрамдас бөлігі пайда болмайды, өйткені мұндай жақтаудағы зарядтар қозғалмайтын болады. Бұл бөлімде индукциялық ЭҚК пайда болуын релятивистік әсермен, қозғалмалы санақ жүйесінде пайда болатын электр өрісінің пайда болуымен түсіндіруге болады. Жарық жылдамдығынан әлдеқайда аз жылдамдықтар үшін бұл өріс келесі формуламен анықталады:
Бұл жағдайда ЭҚК Лоренц күшінің электрлік құрамдас бөлігінің жұмысына байланысты туындайды және оның мәні бірдей мәнге әкеледі.
- жағдайда индукциялық ЭҚКB(t) B(t) магнит өрісі өзгерген кезде кеңістікте пайда болатын құйынды электр өрісініңEқұйынE_{құйын}жұмысына байланысты. Электростатикалық өрістен айырмашылығы, ЕқұйынЕ_{құйын}өрісі потенциалды емес және электр зарядтары болмаған кезде пайда болады. Жергілікті өзара байланысEқұйынE_{құйын}жәнеB(t) B(t) Максвелл электродинамикасының төрт іргелі теңдеулер жүйесіне кіретін келесі теңдеуімен анықталады.
Электромагниттік индукция заңының дифференциалды түрі
Стокс теоремасын құйынды электр өрісінен туындаған L тұйық контурдағы индукция ЭҚК мәнін мына түрде көрсетуге болады:
Осылайша, интегралдық қатынас әмбебап болып табылады, өйткені ол ЭҚК пайда болуының екі нұсқасын да, олардың біріккен әрекетін қоса сипаттайды.
Сызықтық өткізгіш контурдың индуктивтілігі (өзіндік индукция коэффициенті) контурдағы ток күші және осы ток осы тізбек негізінде еркін бет арқылы жасайтын магнит ағыны Ф (I) арасындағы пропорционалдық L коэффициенті болып табылады.
Индуктивтілігі оң, оның вакуумдағы мәні тек контурдың пішіні мен өлшемімен анықталады.
Индуктивтіліктің SI бірлігі Генри (Гн) деп аталады. Тогы бар сызықтық тізбектің магнит өрісінің энергиясы:
Ерікті өткізгіш контурдың индуктивтілігі қатынастан анықталады:
сызықтық контурлардың өзара индукциясының коэффициенті - j-ші контурда магнит өрісі i-ші контур арқылы өтетін токтан/ағып жатқан магнит өрісі жасаған магнит ағынының арасындағы пропорционалдық коэффициенті:
мәні контурлардың пішінімен, өлшемімен және өзара орналасуымен анықталады. Оң деп қабылданатын тізбектердің өзара бағдарына және олардағы токтардың бағыттарына байланысты таңбасы оң және теріс болуы мүмкін. Вакуумда немесе сызықтық магниттік сезімталдығы бар ортада (диа- және парамагнетиктер) өзара индукция коэффициенттері индекстерде симметриялы болады (өзара теорема) .
Тогы бар тізбектер жүйесінің магнит өрісінің энергиясы:
Бұл энергияны екі бөлікке бөлуге болады:
Бірінші мүше контурлардың өзіндік энергияларының қосындысы, екіншісі - оң және теріс болуы мүмкін олардың өзара әрекеттесуінің энергияларының қосындысы. Жалпы энергия әрқашан оң болады.
Ерікті тізбектердің өзара индукция коэффициенті олардың әрекеттесу энергиясымен анықталады
.
- Есептерді шешу әдістері және шығару мысалдары
Тұрақты магнит өрісінде қозғалатын сызықтық өткізгіштердегі индукцияның ЭҚК-ін табу
Шешім әдісі жалпы интегралдық қатынасты қолдану немесе Лоренц күші негізіндегі есептеу болып табылады.
Екі жағдайда да тізбектің сызықтық өткізгіштері бойымен жүргізілетін тізбекті таңдау қажет.
Лоренц күшінің жұмысын есептеу үшін контурлық интегралды есептеуді қажет етеді, сондықтан ол қарапайым контур пішіні үшін ыңғайлы, мысалы, тікбұрышты.
Индукцияның ЭҚК табу үшін қолдану контур ауданы арқылы өтетін ағынды анықтауды, яғни контурмен шектелген бетке интегралдауды талап етеді. Бұл нұсқа қарапайымырақ болады, егер барлық өткізгіштер бір жазықтықта жатса және контур бетіндегі индукцияның қалыпты құраушысының мәні тұрақты болса немесе координаттардың оңай интегралданатын функциясымен берілген.
Жалпы физика курсының типтік есептерін шешу үшін релятивистік қатынасты қолдану көп жағдайда ақталмайды, өйткені ол қажетсіз күрделенуге әкеледі. Бұл әсіресе өткізгіштердің трансляцияланбаған қозғалысы жағдайында, мысалы, олардың айналуы кезінде көрінеді, өйткені өрісті түрлендіру заңы инерциялық санақ жүйесіне жатады.
1-тапсырма (негізгі тапсырма) . Бір жазықтықта ток өтетін ұзын түзу сым және ұзындығы АВ болатын жылжымалы секіргіші бар П-тәрізді ABCD өткізгіші орналасқан. Тізбектің CD жағы өткізгіштен a қашықтықта орналасқан. Секіргіш берілген тұрақты жылдамдықпен қозғалады (2-сурет) . Табу керек:
1) Тізбектегі индукцияның ЭҚК секіргіштен сымға дейінгі қашықтыққа байланысты;
2) контурдағы ток күші, егер оны құрайтын барлық өткізгіштердің бірлік ұзындығына кедергісі тең болса және тізбектің индуктивтілігін елемеуге болады.
Шешуі:
Индукцияның ЭҚК табу (3 әдіс) .
Анық болу үшін токтың бағытын белгілейік (2-сурет) . Контурды айналып өтудің оң бағыты ретінде сағат тіліне қарсы бағытты таңдайық. Сонда контурға нормальдың n векторы сызба жазықтығына перпендикуляр болады және сызбадан бізге бағытталған. Сымнан тізбектің ең жақын өткізгішіне дейінгі қашықтықты a деп белгілейік, сонда қашықтық болады:
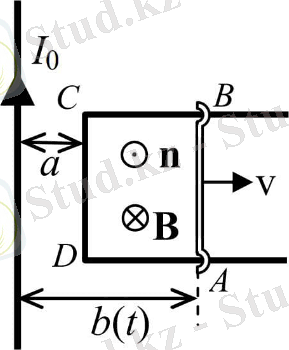
2-сурет. Қозғалыстағы секіргіші бар тізбектегі индукциялық ЭҚК есептеу үшін
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz