Безу теоремасы және Горнер сызбасы: жоғары дәрежелі теңдеулерді шешудің теориясы мен қолданылуы


Мазмұны
Кіріспе 3
І-тарау.
1. 1. Көпмүшеліктер. Көпмүшеліктердің дәрежесі, түбірлері, қалдықпен бөлу.
1. 2. Евклид алгоритмі
1. 3. Өрісте жіктелмейтін көпмүшеліктер
Кіріспе
Үшінші және одан жоғары дәрежелі теңдеулерді шешу қиын. Жалпы рецепттер жоқ. Көп нәрсе шеберлікке, тез тапқырлыққа, байқау мен тәжірибеге байланысты. Мұндай теңдеулерді әрдайым көбейткіштерге жіктеуге болмайды. Жоғары дәрежелі теңдеулерді шешуге көмектесетін әдістердің бірі - Безу теоремасы, Горнер сызбасы.
Зерттеудің өзектілігі.
Безу теоремасының дәлелдемесін тұжырымдау; теоремадан алынған салдарларды анықтау және дәлелдеуін талдау; теореманы және Горнер сызбасын қолданудың нақты мысалдарын көрсету - қазіргі уақытта көкейтесті мәселе болып отыр. Бұл тақырыптар алдын-ала профильдік кластарда оқытылуда.
Зерттеу мақсаты: Жоғары дәрежелі теңдеулерді Безу теоремасын, Горнер сызбасын пайдаланып шешу.
Зерттеу нысаны: Безу теоемасы, Горнер сызбасы.
Зерттеу пәні: орта мектепте сыныптан тыс жұмыстарда, оқушыларды қазіргі заманғы алгебрамен танысуда, ойлау қабілеттерін қалыптастыруда жоғары дәрежелі теңдеулерді және олардың қолданысын пайдалану.
Зерттеу міндеттері:
- Безу теоремасының дәлелдемесін тұжырымдау;
- теоремадан алынған салдарларды анықтау және дәлелдеуін талдау;
- Безу теоремасын қолданудың нақты мысалдарын көрсету;
- Горнер схемасының көмегімен шығарылатын жүйеленген таңдаулы есептерді көрсету.
Зерттеудің әдістемелік негіздері: Білім беру жүйесінің философиялық, психологиялы - педагогикалық, әдістемелік негіздері, ғылыми тәжірибе қағидаларын жасауда орта білім беру үдерісін зерттеудегі жүйелілік, тұлғалылық және іс-әрекет тұрғысынан қараудың жалпы ғылыми ұстанымдары, жеке тұлғаны дамыту саласындағы отандық және шетелдік ғалымдардың еңбектері құрайды.
Зерттеудің теориялық негіздері: іс-әрекеттің философиялық, психологиялық, педагогикалық теориясы; жоғары дәрежелі теңдеулерді зерттеу идеялары және теориялары қолданылды.
Мәселенің зерттелу деңгейі: жоғары дәрежелі теңдеулерді шешу мүмкіндіктері кеңінен қарастырылды, тапсырмалар жинақталды және жүйеленді.
Зерттеу әдістері: Ғылыми және әдістемелік әдебиеттерді талдау, теориялық талдау, материалдарды жинақтап қорытындылау және жоғары дәрежелі теңдеулерді және қасиеттерін осы тәжірибелерге сүйене отырып зерттеу.
Теориялық маңыздылығы: Безу теоремасының, Горнер сызбасының қолданысы көрсетілді, түрлі есептерді тиімді және оңай шешу тәсілдерін табу арқылы олардың қолдану аясы мейлінше кеңірек ашылды.
Зерттеудің практикалық маңыздылығы: Жұмыс нәтижесін жоғары оқу орнының оқу үдерісіндегі алгебра курсында, мектептегі элективті курстарда, оқушыларды қазіргі заманғы алгебрамен таныстыруда және ғылыми жобаларды жазуда пайдалануға болады.
Диплом жұмысының құрылымы кіріспе, екі тарау, қорытынды мен пайдаланылған деректерден тұрады және жалпы көлемі 60 бет.
Безу теоремасының дәлелдемесін тұжырымдау; теоремадан алынған салдарларды анықтау және дәлелдеуін талдау; теореманы және Горнер сызбасын қолданудың нақты мысалдарын көрсету - қазіргі уақытта көкейтесті мәселе болып отыр. Бұл тақырыптар алдын-ала профильдік кластарда оқытылуда.
Этьен Безудің негізгі еңбектері жоғары алгебрамен байланысты, олар алгебралық теңдеулерді шешу теориясын құруға арналған.
Безу теоремасы
x
-қа тәуелді
n
-ші дәрежелі кез келген көпмүшені
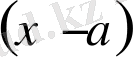 екімүшесіне бөлгенде шыққан қалдық - бөлінгіш көпмүшенің
екімүшесіне бөлгенде шыққан қалдық - бөлінгіш көпмүшенің
 болғандағы мәніне тең.
болғандағы мәніне тең.
Теореманы дәлелдемес бұрын екі түсініктеме берелік. .
1. Құрамына кіретін әріптердің кейбір жеке мәндерінде мағынасын жоғалтатын алгебралық өрнектердің бар екенін білеміз. Мысалы,
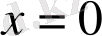 болғанда
болғанда
 мағынасыз;
мағынасыз;
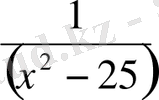 өрнегі
өрнегі
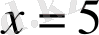 және
және
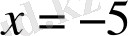 кезінде мағынасын жоғалтады.
кезінде мағынасын жоғалтады.
Кез- келген бүтін оң дәрежелі көпмүшелік ешқашан мағынасын жоғалтпайтынын ескереміз. Айнымалының кез келген мәнінде ол белгілі бір мәнді қабылдайды.
2. Біреуінің мәні нөлге тең, ал екіншісі қандай да бір мәнге ие болатыын екі көбейткіштің көбейтіндісі әрқашан нөлге тең. Егер көбейткіштің біреуі нөлге айналып, ал екіншісінің мағынасы болмаса, онда бұл көбейтіндіні нөлге тең деп айтуға болмайды. Мұндай көбейтінді туралы анық ештеме айту мүмкін емес. Әрбір жағдайда арнайы зерттеу қажет.
Мынадай көбейтіндіні қарастырайық:
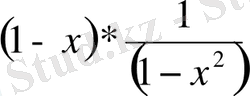 .
.
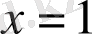 болғанда, бірінші көбейткіш нөлге тең болады, ал екіншісі мағынасыз болады. Бұл көбейтінді
болғанда, бірінші көбейткіш нөлге тең болады, ал екіншісі мағынасыз болады. Бұл көбейтінді
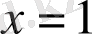 үшін нөлге тең деп тұжырымдауға болмайды.
үшін нөлге тең деп тұжырымдауға болмайды.
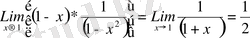
Сонымен,
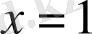 болғанда
болғанда
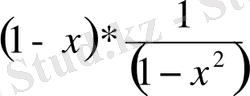 көбейтіндінің мәні жоқ. Бірақ оның шегінің мәні бар, яғни
көбейтіндінің мәні жоқ. Бірақ оның шегінің мәні бар, яғни
 -ге емес
-ге емес
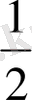 -ге тең.
-ге тең.
Дәлелдеуі:
Бөлінгіш көпмүшені
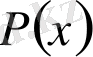 деп белгілейік. Бөлгіш бірінші дәрежелі көпмүше, сондықтан қалдық
R(x
) дәрежеcі нөлге тең, яғни
деп белгілейік. Бөлгіш бірінші дәрежелі көпмүше, сондықтан қалдық
R(x
) дәрежеcі нөлге тең, яғни
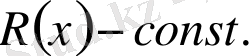
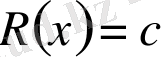 болсын.
болсын.
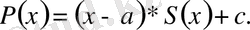
Демек,
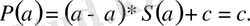
Салдар 1.
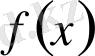 полиномын
полиномын
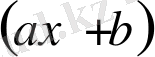 екімүшелігіне бөлгендегі қалдық оcы полиномның
екімүшелігіне бөлгендегі қалдық оcы полиномның
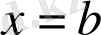 болғандағы мәніне, яғни
болғандағы мәніне, яғни
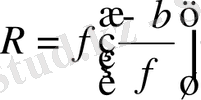 тең болады.
тең болады.
Дәлелдеуі:
Көпмүшеліктерді бөлу ережесіне сәйкес:
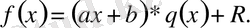
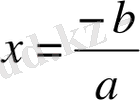 болғанда
болғанда
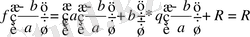 орындалады. Яғни,
орындалады. Яғни,
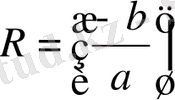 бізге дәлелдеу керегі де осы еді.
бізге дәлелдеу керегі де осы еді.
Салдар 2.
Егер
 саны
саны
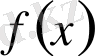 көпмүшелігінің түбірі болса, онда бұл көпмүшелік
көпмүшелігінің түбірі болса, онда бұл көпмүшелік
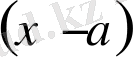 екімүшеліне қалдықсыз бөлінеді.
екімүшеліне қалдықсыз бөлінеді.
Салдар 3.
Егер
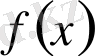 көпмүшелігінің қос-қостан әртүрлі
көпмүшелігінің қос-қостан әртүрлі
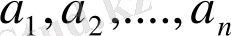 түбірлері бар болса, онда ол көпмүшелік
түбірлері бар болса, онда ол көпмүшелік
 көбейтіндісіне қалдықсыз бөлінеді.
көбейтіндісіне қалдықсыз бөлінеді.
Салдар 4.
Көпмүшенің нөлге тең емес әртүрлі нақты түбірлерінің саны көпмүшенің дәрежесінен артық емес.
Дәлелдеуі.
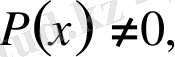 дәрежесі
дәрежесі
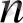 және
және
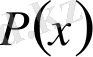 көпмүшесінің әртүрлі
көпмүшесінің әртүрлі
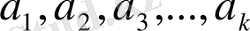 түбірлерінің саны
түбірлерінің саны
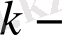 ға тең болсын. Онда 3-салдар бойынша
ға тең болсын. Онда 3-салдар бойынша
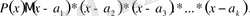
дәр.
дәр.
дәр.
сондықтан
немесе
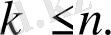
Мысал 1:
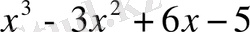 көпмүшелігін
көпмүшелігін
 екімүшесіне бөлгендегі қалдықты табайық.
екімүшесіне бөлгендегі қалдықты табайық.
Безу теоремасы бойынша
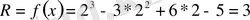
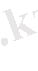
Жауабы:
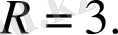
Мысал 2:
 -ның қандай мәнінде
-ның қандай мәнінде
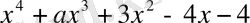 көпмүшелігі
көпмүшелігі
 екімүшесіне қалдықсыз бөлінеді?
екімүшесіне қалдықсыз бөлінеді?
Безу теоремасы бойынша:
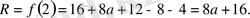 Бірақ
Бірақ
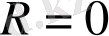 шартына сәйкес,
шартына сәйкес,
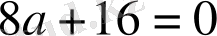 бұдан
бұдан
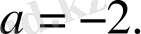
Жауабы:
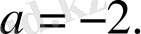
Безу теоремасы француз ғалымы Этьен Безудің атымен аталған алгебраның негізгі теоремаларының бірі. Безу теоремасы көпмүшелердің бөлінгіштігіне байланысты есептерді шешуде, мысалы, көпмүшелерді бөлу кезінде қалдықты табуда, көпмүшелердің еселігін анықтауда және т. б. қолдануды табады деп қорытынды жасауға болады. Сондай-ақ, теореманы пайдаланып көпмүшелерді көбейту, түбірлердің еселігін анықтау және басқа да жіктеулерді орындауға болады.
Этьен Безу - француз математигі, Париж ғылым академиясының мүшесі (1758 жылдан бастап), 1730 жылы 31 наурызда Немурда туып, 1783 жылы 27 қыркүйекте қайтыс болды.
1763 жылдан Безу мичмандар мектебінде, ал 1768 жылдан корольдік артиллерия корпусында математикадан сабақ берді.
Этьен Безудың негізгі еңбектері жоғары алгебрамен байланысты, олар алгебралық теңдеулерді шешу теориясын құруға арналған. Сызықтық теңдеулер жүйесін шешу теориясында анықтауыштар теориясының пайда болуына үлес қосты, жоғары дәрежелі теңдеулер жүйесінен белгісіздерді жою теориясын жасады, екі қисық теореманы (алғаш рет К. Маклаурин тұжырымдаған) дәлелдеді. реті m және n mn артық емес нүктеде қиылысады. Францияда және шетелде 1848 жылға дейін оның 1764-69 жылдары жазған алты томдық «Математика курсы» өте танымал болды. Безу анықталмаған көбейткіштер әдісін жасады, элементар алгебрада осы әдіске негізделген теңдеулер жүйесін шешу әдісі оның атымен аталады. Безу жұмысының бір бөлігі сыртқы баллистикаға арналған. Алгебраның негізгі теоремаларының бірі ғалымның атымен аталады.
Уильям Джордж Хорнер (туылған Уильям Джордж Горнер, 1786 - 22 қыркүйек 1837) - британдық математик, Горнер схемасы оның атымен аталған. Ол сондай-ақ зоотропты өнертапқыш болып саналады. 1786 жылы Англияның Бристоль қаласында дүниеге келген. Ол Бристольдегі Кингсвуд мектебінде білім алған. 16 жасында Кингсвуд мектебінде директордың көмекшісі, ал 4 жылдан кейін директор болды. 1809 жылы ол Бристольді тастап, Батта өз мектебін (Классикалық семинария) құрды.
1819 жылы ол көпмүшенің нақты түбірлерін жуықтап есептеу әдісін жариялады, ол қазір Руффини-Горнер әдісі деп аталады (бұл әдіс қытайлықтарға 13 ғасырда белгілі болған) . Жұмыс Корольдік Қоғамның Философиялық еңбектерінде жарияланған.
19-шы және 20-шы ғасырдың басында Горнер әдісі алгебра бойынша ағылшын және американдық оқулықтарда маңызды орын алды. Де Морган өз еңбектерінде Горнер әдісінің кең мүмкіндіктерін көрсетті.
І-тарау. Көпмүшеліктер
Анықтама
1. 1 Коммутатив K сақинасындағы көпмүше деп
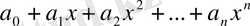 түріндегі формальды қосынды аталады, мұндағы
түріндегі формальды қосынды аталады, мұндағы
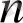 теріс емес бүтін сан,
теріс емес бүтін сан,
 айнымал немесе белгісіз деп аталатын арнайы символ.
айнымал немесе белгісіз деп аталатын арнайы символ.
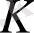 сақинасындағы көпмүшелердің жиыны
сақинасындағы көпмүшелердің жиыны
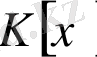 деп белгіленеді.
деп белгіленеді.
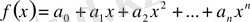 көпмүшесінің
көпмүшесінің
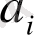 элементтері
элементтері
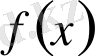 көпмүшесінің коэффициенттері,
көпмүшесінің коэффициенттері,
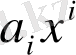 қосылғышы мүшесі деп аталады. Жалғыз мүшеден құралған
қосылғышы мүшесі деп аталады. Жалғыз мүшеден құралған
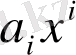 көпмүшесі бірмүше деп аталады. Коэффициенттері бәрі нөлге тең көпмүше нөлдік көпмүше деп аталады және
көпмүшесі бірмүше деп аталады. Коэффициенттері бәрі нөлге тең көпмүше нөлдік көпмүше деп аталады және
 деп белгіленеді.
деп белгіленеді.
Анықтама 1. 2
Егер
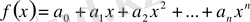 және
және
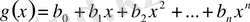 көпмүшелеріне
көпмүшелеріне
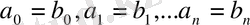 болса, онда
болса, онда
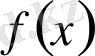 және
және
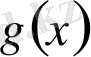 көпмүшелері тең деп аталады.
көпмүшелері тең деп аталады.
Сонымен екі көпмүшенің сәйкес коэффициенттері тең болса, онда олар тең болады.
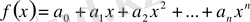 және
және
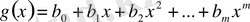 көпмүшелерінің қосындысы
көпмүшелерінің қосындысы
 деп анықталады, мұндағы
деп анықталады, мұндағы
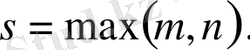
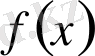 және
және
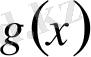 көпмүшелерінің көбейтіндісінің
көпмүшелерінің көбейтіндісінің
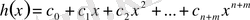 көпмүшесі болады. Оның коэффициенттері
көпмүшесі болады. Оның коэффициенттері
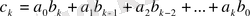 формуласымен есептеледі.
формуласымен есептеледі.
Теорема 1
. Коммутатив
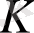 сақинасындағы көпмүшелердің
сақинасындағы көпмүшелердің
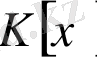 жиыны коммутатив сақина құрайды.
жиыны коммутатив сақина құрайды.
Дәлелдеу . Екі көпмүшенің қосындысы және көбейтіндісі көпмүше болатыны анықтамадан шығады.
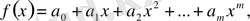
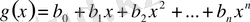 және
және
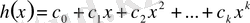 көпмүшелері берілсін және
көпмүшелері берілсін және
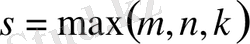 болсын. Онда
болсын. Онда
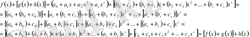
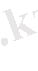 Берілген көпмүшелердің коэффициенттері
Берілген көпмүшелердің коэффициенттері
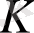 сақинасының элементтері болғанлықтан, коэффициенттерге қосудың ассоциативтілігі орындалады. Осы алдыңғы теңдіктерде қолданылды. Сөйтіп, көпмүшелердің қосуына ассоциативтік ереже орындалады
сақинасының элементтері болғанлықтан, коэффициенттерге қосудың ассоциативтілігі орындалады. Осы алдыңғы теңдіктерде қолданылды. Сөйтіп, көпмүшелердің қосуына ассоциативтік ереже орындалады
 .
.
Нөлдік көпмүшені
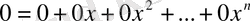 деп келтіруге болады. Егер
деп келтіруге болады. Егер
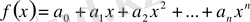 көпмүшесі берілсе, онда
көпмүшесі берілсе, онда
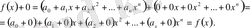
Oсыған ұқсас
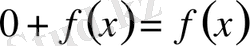 екенін де көрсетуге болады. Сондықтан нөлдік көпмүше қосуға қатынасты бейтарап элемент болады.
екенін де көрсетуге болады. Сондықтан нөлдік көпмүше қосуға қатынасты бейтарап элемент болады.
Енді
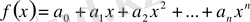 көпмүшесі үшін
көпмүшесі үшін
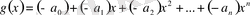 деп алайық. Онда қосудың анықтамасы бойынша,
деп алайық. Онда қосудың анықтамасы бойынша,
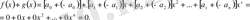
Осыған ұқсас
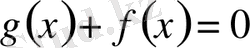 теңдігі көрсетіледі. Сондықтан
теңдігі көрсетіледі. Сондықтан
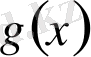 көпмүшесі
көпмүшесі
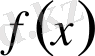 көпмүшесіне қарама-қарсы болады.
көпмүшесіне қарама-қарсы болады.
Егер
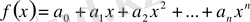 ,
,
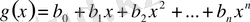 берілсе, онда
берілсе, онда
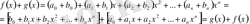
Сондықтан қосуға коммутативтік ереже орындалады.
Сөйтіп, көпмүшелер қосуға қатынасты коммутатив топ құрайды.
Енді
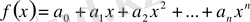 ,
,
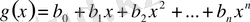 және
және
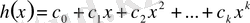 көпмүшелері берілсін. Одан әрі
көпмүшелері берілсін. Одан әрі
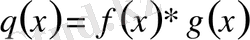 ,
,
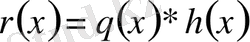 ,
,
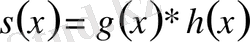 ,
,
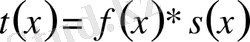 және
және
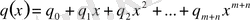 ,
,
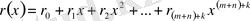 ,
,
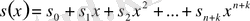 ,
,
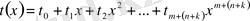 болсын. Көбейтудің анықтамасы бойынша,
болсын. Көбейтудің анықтамасы бойынша,
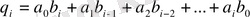 ,
,
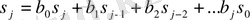 ,
,
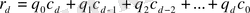 ,
,
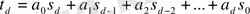 . Осыдан
. Осыдан
 Соңғы өрнектегі мүшелерді басқаша топтаса, онда
Соңғы өрнектегі мүшелерді басқаша топтаса, онда
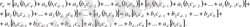 Мұнда квадрат жақшаларда осы ретте алынған
Мұнда квадрат жақшаларда осы ретте алынған
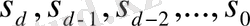 коэффициенттері болатынын көруге болады. Сондықтан
коэффициенттері болатынын көруге болады. Сондықтан
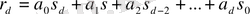 . Ал бұл
. Ал бұл
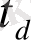 коэффициенті де болады. Сөйтіп, кез келген
коэффициенті де болады. Сөйтіп, кез келген
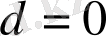 ,
,
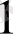 ,
,
 , …,
, …,
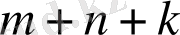 үшін
үшін
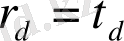 . Сондықтан
. Сондықтан
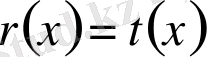 немесе
немесе
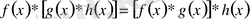 . Бұл ассоциативтік теңдігі.
. Бұл ассоциативтік теңдігі.
Осыған ұқсас дистрибутивтік ережесі орындалатынын көрсетуге болады:
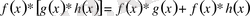 және
және
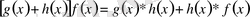 . Оған қоса,
. Оған қоса,
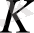 сақинасы коммутатив болса, онда копмүшелердің көбейтуі коммутатив болатынын да осылай көрсетуге болады.
сақинасы коммутатив болса, онда копмүшелердің көбейтуі коммутатив болатынын да осылай көрсетуге болады.
Енді көпмүшелердің
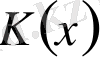 жиынында көбейтуге қатысты бейтарап элемент табылатынын көрсетейік.
жиынында көбейтуге қатысты бейтарап элемент табылатынын көрсетейік.
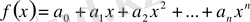 көпмүшесі берілсін. Онда
көпмүшесі берілсін. Онда
 . Осыған ұқсас
. Осыған ұқсас
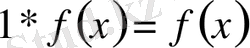 теңдігін де көрсетуге болады. Сөйтіп,
теңдігін де көрсетуге болады. Сөйтіп,
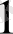 көпмүшесі көбейтуге қатысты бейтарап элемент болады.
көпмүшесі көбейтуге қатысты бейтарап элемент болады.
Сонымен, коммутатив
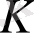 сақинасындағы көпмүшелердің
сақинасындағы көпмүшелердің
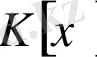 жиыны коммутатив сақина құрайды.
жиыны коммутатив сақина құрайды.
Анықтама
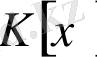 сақинасы
сақинасы
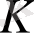 сақинасындағы бір айнымалды көпмүшелер сақинасы деп аталады.
сақинасындағы бір айнымалды көпмүшелер сақинасы деп аталады.
Екі
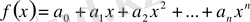 және
және
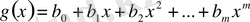 көпмүшелерінің көбейтіндісін есептегенде көбейтіндінің коэффициенттерін
көпмүшелерінің көбейтіндісін есептегенде көбейтіндінің коэффициенттерін
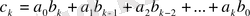 формуласымен іздемей, сақинаның жоғары дәлелденген қасиеттері пайдалануға болады. Екі көпмүше сәйкесінше
формуласымен іздемей, сақинаның жоғары дәлелденген қасиеттері пайдалануға болады. Екі көпмүше сәйкесінше
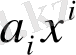 және
және
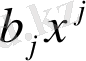 бірмүшелерінің қосындысы болады. Сондықтан көпмүшелердің көбейтіндісі
бірмүшелерінің қосындысы болады. Сондықтан көпмүшелердің көбейтіндісі
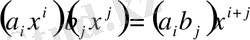 көбейтінділерінің қосындысы болады:
көбейтінділерінің қосындысы болады:
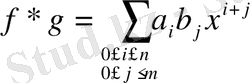
Анықтама
.
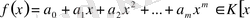 көпмүшесінің дәрежесі деп
көпмүшесінің дәрежесі деп
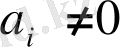 болатын ең үлкен теріс емес бүтін
болатын ең үлкен теріс емес бүтін
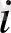 саны аталады және
саны аталады және
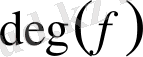 деп белгіленеді.
деп белгіленеді.
Кей кезде нөлдік көпмүшенің дәрежесі
 деп алынады:
деп алынады:
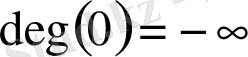 .
.
Теорема.
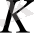 коммутатив сақина болсын. Онда кез келген
коммутатив сақина болсын. Онда кез келген
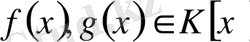 көпмүшелері үшін келесі қасиеттер орындалады.
көпмүшелері үшін келесі қасиеттер орындалады.
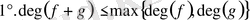 .
.
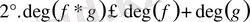 , мұнда
, мұнда
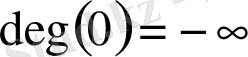 деп алынды.
деп алынды.
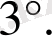 Егер
Егер
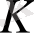 біртұтастық аймақ болса, онда
біртұтастық аймақ болса, онда
 .
.
Теорема
Егер
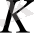 біртұтастық аймақ болса, онда
біртұтастық аймақ болса, онда
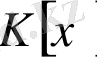 сақинасы да біртұтас аймақ болады.
сақинасы да біртұтас аймақ болады.
Теоремa.
Егер
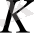 біртұтас аймақ болса, онда
біртұтас аймақ болса, онда
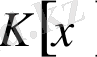 сақинасының бөлінділер өрісі табылады.
сақинасының бөлінділер өрісі табылады.
Дәлелдеу
. Сақиналар теориясында кез келген біртұтастық аймақтың бөлінділер өрісі болатыны дәлелденеді. Онда
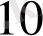 -теорема бойынша,
-теорема бойынша,
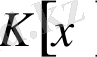 біртұтастық аймақ болады. Сондықтан
біртұтастық аймақ болады. Сондықтан
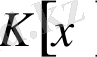 біртұтас аймақтың бөлінділер өрісі болады.
біртұтас аймақтың бөлінділер өрісі болады.
 екімүшесіне қалдықпен бөлу. Безу теоремасы
екімүшесіне қалдықпен бөлу. Безу теоремасы
Теорема
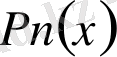 көпмүшелігін
көпмүшелігін
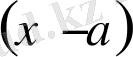 екімүшесіне бөлгендегі қалдық көпмүшенің
екімүшесіне бөлгендегі қалдық көпмүшенің
 болғандағы мәніне тең.
болғандағы мәніне тең.
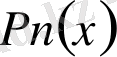 -
-
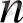 дәрежелі көпмүшелік,
дәрежелі көпмүшелік,
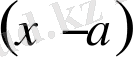 - оның бөлгіші,
- оның бөлгіші,
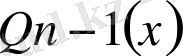 -
-
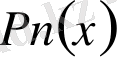 -ті
-ті
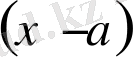 бөлгендегі бөліндісі
бөлгендегі бөліндісі
(
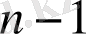 дәрежелі көп мүшелік) ,
дәрежелі көп мүшелік) ,
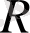 - қалдық (
- қалдық (
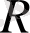 қалдығында
қалдығында
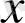 болмайды) .
болмайды) .
Дәлелі :
Көпмүшені қалдықпен бөлу ережесі бойынша:
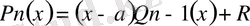 .
.
Осыдан шығатыны
 :
:

Демек,
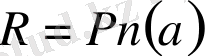 , яғни көпмүшеліктің
, яғни көпмүшеліктің
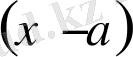 бөлгендегі қалдығы көпмүшеліктің
бөлгендегі қалдығы көпмүшеліктің
 тең болғандағы мәніне тең. Дәлелденді.
тең болғандағы мәніне тең. Дәлелденді.
Теорема салдарлары
Салдар 3. 1
:
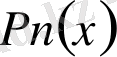 көпмүшелігін
көпмүшелігін
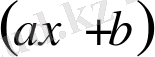 екімүшесіне бөлгендегі қалдық көпмүшенің
екімүшесіне бөлгендегі қалдық көпмүшенің
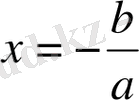 болғандағы мәніне тең, яғни
болғандағы мәніне тең, яғни
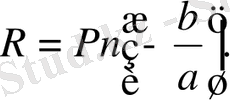
Дәлелі : Көпмүшені қалдықпен бөлу ережесі бойынша:
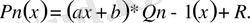
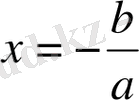 болғанда:
болғанда:
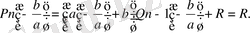
Демек,
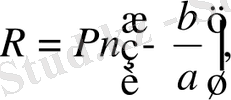 дәлелденді.
дәлелденді.
Салдар 3. 2
:
Егер
 саны
саны
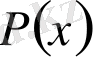 көпмүшелігінің түбірі болса,
көпмүшелігінің түбірі болса,
онда бұл көпмүшелік
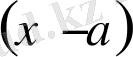 екімүшесіне қалдықсыз бөлінеді.
екімүшесіне қалдықсыз бөлінеді.
Дәлелі: Безу теоремасы бойынша
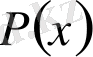 көпмүшелігін
көпмүшелігін
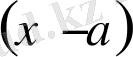 бөлгендегі қалдығы
бөлгендегі қалдығы
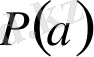 тең, ал шарт бойынша
тең, ал шарт бойынша
 саны
саны
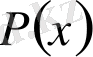 көпмүшелігінің түбірі, яғни
көпмүшелігінің түбірі, яғни
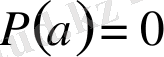 , дәлелденді.
, дәлелденді.
Безу теоремасының осы қорытындысынан
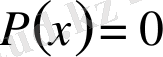 теңдеуін шешу есебі
теңдеуін шешу есебі
 көпмүшесінің бірінші дәрежелі (сызықтық бөлгіштері) бар бөлгіштерін таңдау есебіне тең екенін көруге болады.
көпмүшесінің бірінші дәрежелі (сызықтық бөлгіштері) бар бөлгіштерін таңдау есебіне тең екенін көруге болады.
Мысал:
 саны келесі көпмүшелікке неше еселі екенін анықтаңыз.
саны келесі көпмүшелікке неше еселі екенін анықтаңыз.
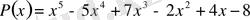 .
.
_
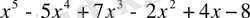

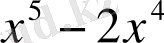
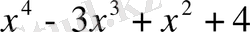
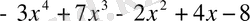
¯
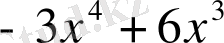
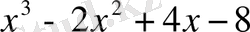
¯
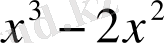
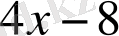
¯
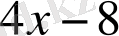

_
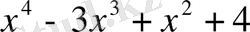

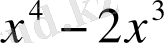
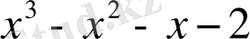
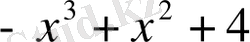
¯
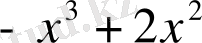
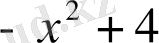
¯
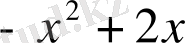
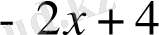
¯
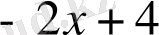

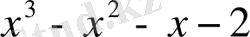
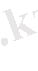

¯
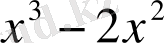
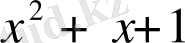
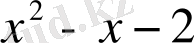
¯
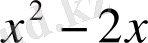

¯


Жауабы:
 түбірі
түбірі
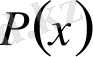 көпмүшелігінe
көпмүшелігінe
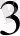 еселі түбір.
еселі түбір.
 элементі үшін
элементі үшін
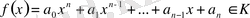 көпмүшесінің
көпмүшесінің
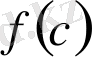 мәні
мәні
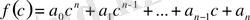 деп анықталады.
деп анықталады.
Қосу және көбейту алгебралық операция болғандықтан көпмүшенің мәні бірмәнді анықталады.
Теорема
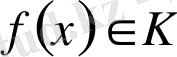 көпмүшесі берілсін. Кез келген
көпмүшесі берілсін. Кез келген
 үшін
үшін
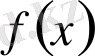 көпмүшесін
көпмүшесін
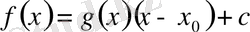 түрінде бірмәнді жазуға болады, мұндағы
түрінде бірмәнді жазуға болады, мұндағы
 , сонымен бірге
, сонымен бірге
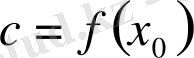 болады.
болады.
Дәлелдеу
.
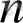 -дәрежелі
-дәрежелі
 көпмүшесі берілсін. Егер
көпмүшесі берілсін. Егер
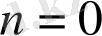 болса, онда
болса, онда
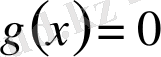 ,
,
 деп алуға болады. Сонымен бірге осы келтіру бірмәнді болады. Енді
деп алуға болады. Сонымен бірге осы келтіру бірмәнді болады. Енді
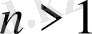 болсын. Көпмүшедегі
болсын. Көпмүшедегі
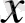 -тың дәрежелерін кемімелі түрде жазайық:
-тың дәрежелерін кемімелі түрде жазайық:
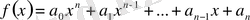 . Егер
. Егер
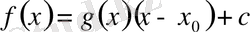 түрінде келтіру болса, онда
түрінде келтіру болса, онда
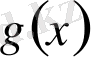 -ты анықталмаған коэфициенттермен алайық:
-ты анықталмаған коэфициенттермен алайық:
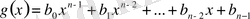 . Онда
. Онда
 Осы теңдіктің екі жағындағы
Осы теңдіктің екі жағындағы
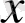 -тың дәрежелеріндегі сәйкес коэфициенттерін теңестірейік:
-тың дәрежелеріндегі сәйкес коэфициенттерін теңестірейік:
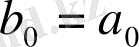 ,
,
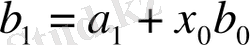 ,
,
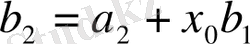 ,
,
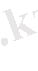
. . .

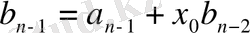 ,
,
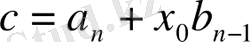 .
.
Осы формулалар бойынша біртіндеп
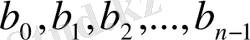 және
және
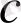 коэффициентерінің мәндерін табуға болады. Сондықтан теореманың шартын қанағаттандыратын
коэффициентерінің мәндерін табуға болады. Сондықтан теореманың шартын қанағаттандыратын
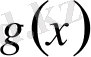 көпмүшесі және
көпмүшесі және
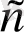 элементі табылады және олар бірмәнді анықталады.
элементі табылады және олар бірмәнді анықталады.
Енді
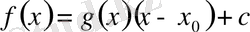 формуласына
формуласына
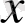 -тың орнына
-тың орнына
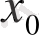 мәнін қойса, онда
мәнін қойса, онда
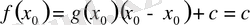 . Осымен теорема дәлелденді.
. Осымен теорема дәлелденді.
Теоремадағы
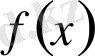 көпмүшесі - бөлінгіш,
көпмүшесі - бөлінгіш,
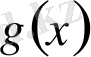 - толымсыз бөлінді,
- толымсыз бөлінді,
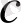 - қалдық,
- қалдық,
 екімүшесі - бөлгіш деп аталады.
екімүшесі - бөлгіш деп аталады.
Егер
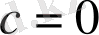 болса, онда
болса, онда
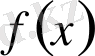 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді дейді және оны сандарға сияқты
екімүшесіне бөлінеді дейді және оны сандарға сияқты
 деп белгілейміз.
деп белгілейміз.
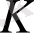 сақинасының
сақинасының
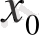 элементі
элементі
 көпмүшесінің түбірі деп аталады, егер
көпмүшесінің түбірі деп аталады, егер
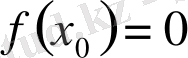 болса.
болса.
 Теңдіктердегі формулалар
Теңдіктердегі формулалар
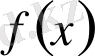 -ты
-ты
 -қа бөлудің ыңғайлы сұлбасын береді. Ол Горнер сұлбасы деп аталады.
-қа бөлудің ыңғайлы сұлбасын береді. Ол Горнер сұлбасы деп аталады.
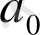
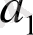
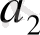
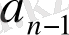
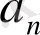
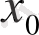
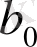
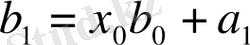

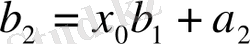
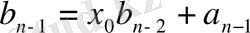
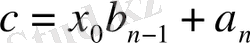
Ол былай толтырылады.
1) Әуелі бірінші жолда
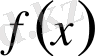 көпмүшесінің коэффициенттері жазылады.
көпмүшесінің коэффициенттері жазылады.
2)
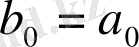 деп алынады.
деп алынады.
3) Келесі
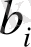 коэффициенті
коэффициенті
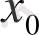 -ді алдынғы
-ді алдынғы
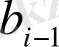 -ге көбейтіліп,
-ге көбейтіліп,
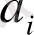 -ге қосылады:
-ге қосылады:
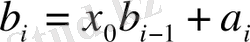 .
.
Мысалдар
. 1)
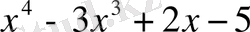 көпмүшесін
көпмүшесін
 екімүшесіне бөлейік.
екімүшесіне бөлейік.
Бұл жағдайда
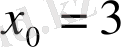 . Бөлінгіштің коэффициенттері
. Бөлінгіштің коэффициенттері
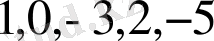 болады. Оны бірінші жолға жазамыз.
болады. Оны бірінші жолға жазамыз.
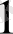
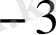


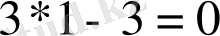
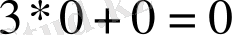
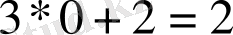
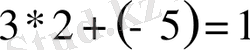
Сонымен
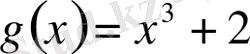 , қалдық
, қалдық
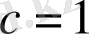 және
және
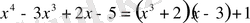 .
.
2)
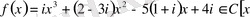
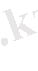 көпмүшесінің
көпмүшесінің
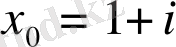 санындағы мәнін табайық.
санындағы мәнін табайық.
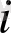

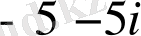
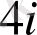
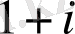
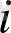
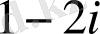
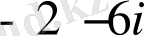

Сондықтан
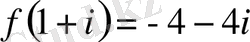 .
.
Мысал
2
.
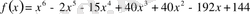 көпмүшесінің
көпмүшесінің
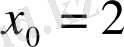 түбірінің еселігін табайық. Ол үшін Горнер схемасын пайдаланамыз.
түбірінің еселігін табайық. Ол үшін Горнер схемасын пайдаланамыз.
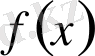
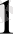
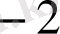
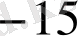
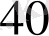
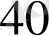
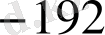
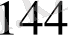
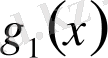



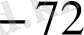

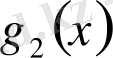

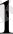

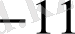
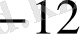
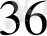

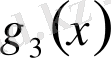


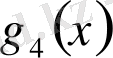

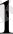
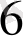
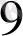

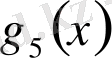

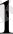
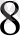
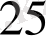
Мұнда әрбір адымдағы қалдықтары астынан сызылған. Соңғы,
 -адымда қалдық нөлден өзгеше, сондықтан
-адымда қалдық нөлден өзгеше, сондықтан
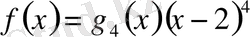 және
және
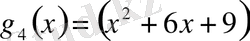

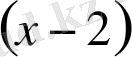 . Сөйтіп,
. Сөйтіп,
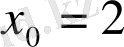 түбірінің еселігі
түбірінің еселігі
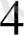 -ке тең.
-ке тең.
Теорема.
Егер
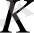 біртұтастық аймақ болса, онда
біртұтастық аймақ болса, онда
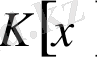 сақинасының кез келген
сақинасының кез келген
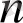 дәрежелі көпмүшенің түбірлерінің саны
дәрежелі көпмүшенің түбірлерінің саны
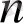 -нан артық болмайды.
-нан артық болмайды.
Дәлелдеу
. Нөлден өзге
 көпмүшесінің дәрежесі
көпмүшесінің дәрежесі
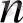 болсын.
болсын.
Егер
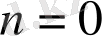 болса, онда
болса, онда
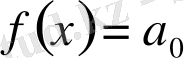 ,
,
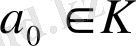 . Сондықтан көпмүшенің түбірі болмайды. Бұл жағдайда теорема орындалады.
. Сондықтан көпмүшенің түбірі болмайды. Бұл жағдайда теорема орындалады.
Енді
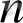 үшін теорема орындалсын, яғни кез келген
үшін теорема орындалсын, яғни кез келген
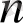 -дәрежелі көпмүшенің түбірлер саны
-дәрежелі көпмүшенің түбірлер саны
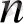 -нен аспасын.
-нен аспасын.
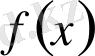 -тың дәрежесі
-тың дәрежесі
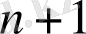 болсын. Егер оның түбірі болмаса, онда теорема орындалады
болсын. Егер оның түбірі болмаса, онда теорема орындалады
 .
.
Егер оның түбірі
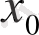 болса, онда Безу теоремасы бойынша,
болса, онда Безу теоремасы бойынша,
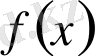 көпмүшесі
көпмүшесі
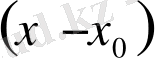 -ге бөлінеді:
-ге бөлінеді:
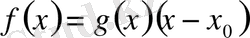 . Ал
. Ал
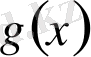 көпмүшесінің дәрежесі
көпмүшесінің дәрежесі
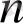 болады және, индукцияның жорымы бойынша,
болады және, индукцияның жорымы бойынша,
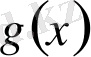 -тің түбірлерінің саны
-тің түбірлерінің саны
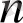 -нен аспайды. Осыдан
-нен аспайды. Осыдан
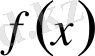 көпмүшесінің түбірлерінің саны
көпмүшесінің түбірлерінің саны
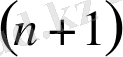 -ден аспайды.
-ден аспайды.
Математикалық индукция принципі бойынша, теорема кез келген натурал
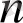 саны үшін орындалады, яғни кез келген
саны үшін орындалады, яғни кез келген
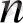 -дәрежелі көпмүшенің түбірлерінің саны
-дәрежелі көпмүшенің түбірлерінің саны
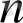 -нан артық болмайды.
-нан артық болмайды.
Математикалық анализде көпмүше функция ретінде анықталады. Егер екі функцияның анықталу аймағындағы кез келген нүктеде функциялардың мәндері тең болса, онда функциялар тең болады.
Анықтама
(көпмүшелердің
функциялық теңдігі
) .
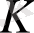 біртұтастық аймақ болсын.
біртұтастық аймақ болсын.
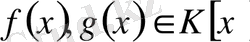 көпмүшелері берілсін. Егер кез келген
көпмүшелері берілсін. Егер кез келген
 элементі үшін
элементі үшін
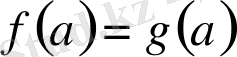 болса, онда
болса, онда
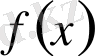 ,
,
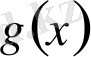 көпмүшелері тең болады,
көпмүшелері тең болады,
Көпмүшелердің бұрын анықталған теңдігін (сәйкес коэффициенттер теңдігі арқылы) алгебралық теңдігі деп аталады.
Теорема.
(Көпмүшелердің алгебралық және функциялық теңдігі туралы) . Егер
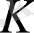 ақырсыз біртұтастық аймақ болса, онда
ақырсыз біртұтастық аймақ болса, онда
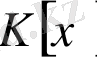 сақинасындағы көпмүшелердің функциялық теңдігінен алгебралық теңдігі шығады.
сақинасындағы көпмүшелердің функциялық теңдігінен алгебралық теңдігі шығады.
Дәлелдеу
.
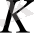 ақырсыз біртұтастық аймақ болсын және
ақырсыз біртұтастық аймақ болсын және
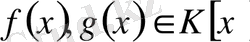 көпмүшелерінің дәрежелері
көпмүшелерінің дәрежелері
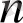 және кез келген
және кез келген
 үшін
үшін
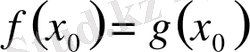 болсын. Одан әрі
болсын. Одан әрі
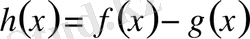 болсын. Онда кез келген
болсын. Онда кез келген
 үшін
үшін
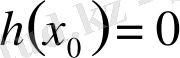 . Ал
. Ал
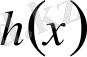 көпмүшесінің дәрежесі
көпмүшесінің дәрежесі
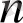 -нен аспайды және
-нен аспайды және
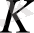 сақинасы ақырсыз, сондықтан
сақинасы ақырсыз, сондықтан
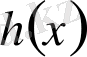 көпмүшесі нөлдік көпмүше болады. Осыдан
көпмүшесі нөлдік көпмүше болады. Осыдан
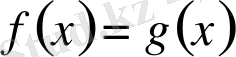 .
.
Сонымен, егер
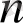 -дәрежелі
-дәрежелі
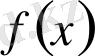 көпмүшесінің
көпмүшесінің
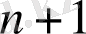 нүктедегі мәндері берілсе, атап айтқанда,
нүктедегі мәндері берілсе, атап айтқанда,
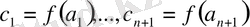 мәндері онда
мәндері онда
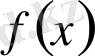 көпмүшесі бірмәнді анықталады. Берілген мәндер бойынша көпмүшені анықтау үшін әртүрлі формулалар қолданылады. Соның арасында
Лагранждың интерполяциялық формуласы
:
көпмүшесі бірмәнді анықталады. Берілген мәндер бойынша көпмүшені анықтау үшін әртүрлі формулалар қолданылады. Соның арасында
Лагранждың интерполяциялық формуласы
:
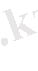
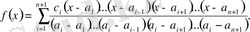
Мысалы, коэффициенттері белгісіз
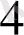 -дәрежелі
-дәрежелі
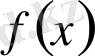 көпмүшесінің мәндері кестемен берілсін:
көпмүшесінің мәндері кестемен берілсін:
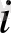
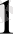

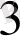
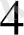
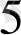
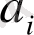
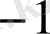


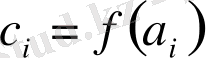


Ізделінген көпмүше Лагранж формуласымен анықталады:
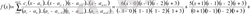

Теорема
(Қалдықпен бөлу туралы теорема) .
 өріс және
өріс және
 ,
,
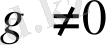 , көпмүшелері берілсін. Онда
, көпмүшелері берілсін. Онда
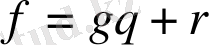 және
және
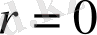 немесе
немесе
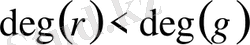

болатындай
 көпмүшелері бірмәнді табылады.
көпмүшелері бірмәнді табылады.
Дәлелдеу.
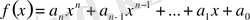 ,
,
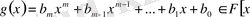 көпмүшеfлері берілсін. Оған қоса,
көпмүшеfлері берілсін. Оған қоса,
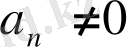 және
және
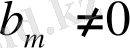 болсын. Егер
болсын. Егер
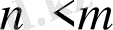 болса, онда
болса, онда
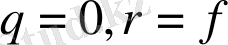 деп аламыз. Одна әрі
деп аламыз. Одна әрі
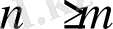 болсын. Егер
болсын. Егер
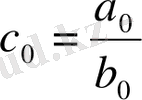 және
және
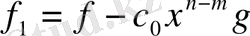 болса, онда
болса, онда
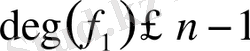 . Енді
. Енді
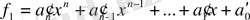 болсын. Онда
болсын. Онда
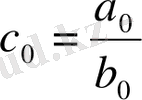 және
және
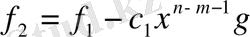 деп аламыз. Ал
деп аламыз. Ал
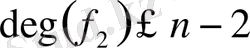 . Осы процесті жалғастыра берсе, көпмүшелердің
. Осы процесті жалғастыра берсе, көпмүшелердің
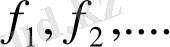 тізбегі шығады және
тізбегі шығады және
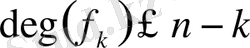 . Ең соңғы дәрежесі
. Ең соңғы дәрежесі
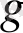 көпмүшесінің дәрежесінен кем көпмүшесі,
көпмүшесінің дәрежесінен кем көпмүшесі,
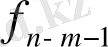 көпмүшесі болады. Олай болса,
көпмүшесі болады. Олай болса,
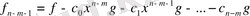 болады. Осыдан
болады. Осыдан
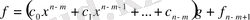 . Онда
. Онда
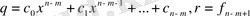 көпмүшелері үшін теореманың шарттары орындалады.
көпмүшелері үшін теореманың шарттары орындалады.
Енді
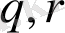 көпмүшелерінің бірмәнділігін көрсетейік.
көпмүшелерінің бірмәнділігін көрсетейік.
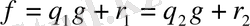 , болсын, сонымен бірге
, болсын, сонымен бірге
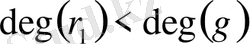 және
және
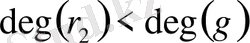 болса, онда
болса, онда
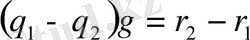 .
.
Егер
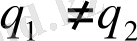 болса, онда
болса, онда
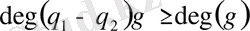 . Ал
. Ал
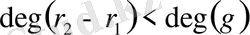 . Сондықтан
. Сондықтан
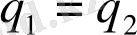 , ал осыдан
, ал осыдан
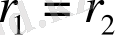 . Теорема дәлелденді.
. Теорема дәлелденді.
Евклид сақинасы
деп келесі шарттар орындалатын
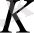 біртұтастық аймақ аталады:
біртұтастық аймақ аталады:
1) Кез келген нөлден өзге
 элементіне теріс емес бүтін
элементіне теріс емес бүтін
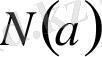 саны сәйкес беріледі.
саны сәйкес беріледі.
2) Кез келген
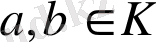 ,
,
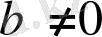 , элементтері үшін
, элементтері үшін
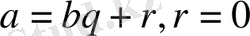 немесе
немесе
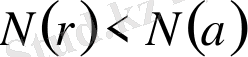

болатындай
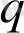 және
және
 элементтері табылады [6] .
элементтері табылады [6] .
Салдар 1
. Егер
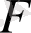 өріс болса, онда
өріс болса, онда
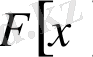 сақинасы Евклид сақинасы болады.
сақинасы Евклид сақинасы болады.
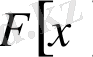 сақинасында
сақинасында
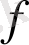 көпмүшесі үшін
көпмүшесі үшін
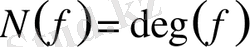 деп алу керек. Сондықтан, қалдықпен бөлу туралы теорема бойынша, орындалатын
деп алу керек. Сондықтан, қалдықпен бөлу туралы теорема бойынша, орындалатын
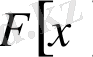 сақинасы Евклид сақинасы болады.
сақинасы Евклид сақинасы болады.
Келесі екі салдар Евклид сақинасы бас идеалдар сақинасы, бас идеалдар сақинасы факториалдық сақина болатынынан шығады.
Салдар 2
. Егер
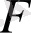 өріс болса, онда
өріс болса, онда
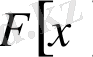 сақинасы бас идеалдар сақина болады.
сақинасы бас идеалдар сақина болады.
Салдар 3
. Егер
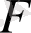 өріс болса, онда
өріс болса, онда
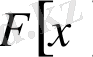 сақинасы факториалдық сақина болады.
сақинасы факториалдық сақина болады.
Мысал
.
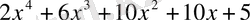 көпмүшесін
көпмүшесін
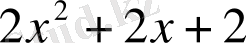 көпмүшесіне қалдықпен бөлейік. Бөлуді баған түрінде келтіруге болады.
көпмүшесіне қалдықпен бөлейік. Бөлуді баған түрінде келтіруге болады.
бөлінді
↓
бөлгіш
↓
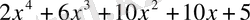
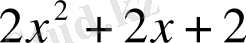
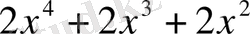
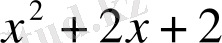
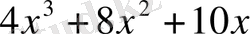
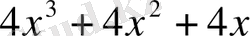
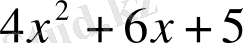
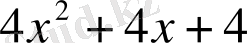
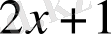 ←
←
Сонымен
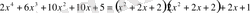 .
.
Бүтін сандарға сияқты берілген көпмүшелердің ортақ бөлгіші деп берілген көпмүшелерді бөлетін көпмүше аталады. Берілген көпмүшелердің ең үлкен ортақ бөлгіші деп берілген көпмүшелердің кез келген ортақ бөлгішіне бөлінетін ортақ бөлгіші аталады.
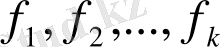 көпмүшелерінің ең үлкен ортақ бөлгіші әдетте
көпмүшелерінің ең үлкен ортақ бөлгіші әдетте
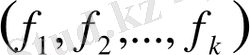 деп белгіленеді.
деп белгіленеді.
Егер
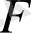 өрісі үшін
өрісі үшін
 және
және
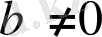 , болса,
, болса,
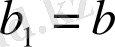 деп алып, қалдықпен бөлу процесін бастаймыз:
деп алып, қалдықпен бөлу процесін бастаймыз:
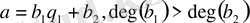 ,
,
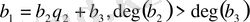 ,
,

. . .
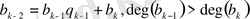 ,
,
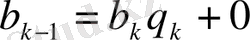 .
.
Осы процесті нөлдік қалдық шыққанша жалғастыру керек.
Ал
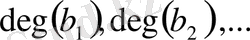 тізбегі кемімелі болады, сондықтан ол ақырлы адымнан кейін үзіледі. Енді
тізбегі кемімелі болады, сондықтан ол ақырлы адымнан кейін үзіледі. Енді
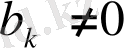 және
және
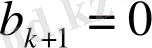 болсын. Онда
болсын. Онда
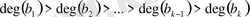 . Бүтін сандарға сияқты
. Бүтін сандарға сияқты
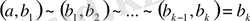 екенін көрсетуге болады мұндағы
екенін көрсетуге болады мұндағы
 одақтастырылғандық белгісі. Сондықтан
одақтастырылғандық белгісі. Сондықтан
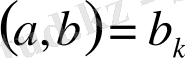 және келесі теорема дәлелденді.
және келесі теорема дәлелденді.
Осы біртіндеп қалдықпен бөлу процесі Евклид алгоритмі деп аталады.
Теорема 2. 6. 1
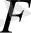 өрісіндегі кез келген нөлден өзгеше екі көпмүшенің ең үлкен ортақ бөлгіші табылады.
өрісіндегі кез келген нөлден өзгеше екі көпмүшенің ең үлкен ортақ бөлгіші табылады.
Теорема 2. 6. 2 (Ең үлкен ортақ бөлгішті сызықтық түрде келтіру туралы) . Егер
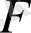 өріс,
өріс,
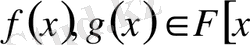 және
және
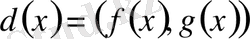 болса, онда кейбір
болса, онда кейбір
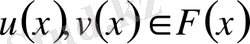 көпмүшелері үшін
көпмүшелері үшін
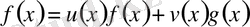 .
.

Дәлелдеу.
 -жүйені басқа түрде жазайық:
-жүйені басқа түрде жазайық:
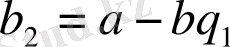 ,
,
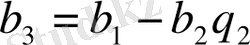 , (5)
, (5)
. . .
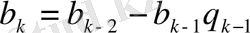 .
.
Бірінші теңдікте,
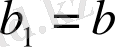 болғандықтан
болғандықтан
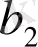 көпмүшесі
көпмүшесі
 және
және
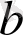 көпмүшелері арқылы сызықтық түрде өрнектелді:
көпмүшелері арқылы сызықтық түрде өрнектелді:
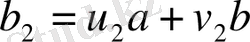 . Табылған өрнекті екінші теңдікте
. Табылған өрнекті екінші теңдікте
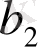 -нің орнына қойып ұқсас мүшелерді біріктірме,
-нің орнына қойып ұқсас мүшелерді біріктірме,
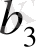 -ті
-ті
 және
және
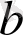 арқылы сызықтық түрде келтіруге болады:
арқылы сызықтық түрде келтіруге болады:
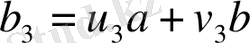 . Осы процесті жоғарыдан төменге қарай жалғастыра берсе, нәтижесінде
. Осы процесті жоғарыдан төменге қарай жалғастыра берсе, нәтижесінде
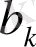 көпмүшесі
көпмүшесі
 және
және
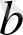 арқылы сызықтық түрде келтіріледі:
арқылы сызықтық түрде келтіріледі:
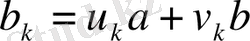
 .
.
Мысалдар. 1)
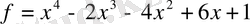 және
және
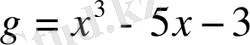 көпмүшелерінің ең үлкен ортақ бөлгішін сызықтық түрде келтірейік. Ол үшін Евклид алгоритмін қолданамыз.
көпмүшелерінің ең үлкен ортақ бөлгішін сызықтық түрде келтірейік. Ол үшін Евклид алгоритмін қолданамыз.
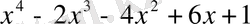
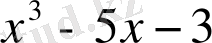
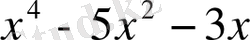
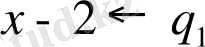
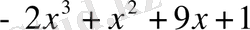
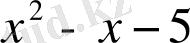
Сонымен,
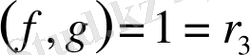 . Евклид алгоритмі бойынша,
. Евклид алгоритмі бойынша,
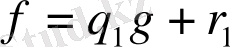 ,
,
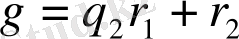 ,
,
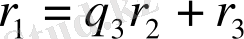 .
.
Осыдан
r 1 = f - q 1 g ,
r 2 = g - q 2 r 1 ,
r 3 = r 1 - q 3 r 2 ,
мұнда q 1 = x - 2, r 1 = x 2 - x - 5, q 2 = x + 1, r 2 = x + 2, q 3 = x - 3, r 3 = 1.
Енді бірінші теңдіктегі r 1 -дің мәнін екінші теңдікке қоямыз: r 2 = g - q 2 r 1 = g - q 2 ( f - q 1 g ) = g - q 2 f + q 1 q 2 g = - q 2 f + (1 + q 1 q 2 ) g .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz