Математикалық амалдарды ағылшын тілінде оқыту әдістері


Пән: Математиканы ағылшын тілінде оқыту.
Тақырып: Математикалық амалдарды ағылшын тілінде үйрету тәсілдері.
Тобы: МБ-18-01
Ғылыми жетекші: Шадимуратова М. М
Студент: Ерғали Жанерке
МазмұныКіріспе3
І Математикалық амалдарды ағылшын тілінде үйрету тәсілдері5
1. 1 Математика шет тілін меңгеру құралы ретінде5
1. 2 Ағылшын тілі сабақтарында математикалық сауаттылықты қалыптастыру16
1. 3 Практикалық бөлім20
Қорытынды. 24
Пайдаланған әдебиеттер26
Кіріспе
Қазақстандағы білім берудің аса маңызды стратег лық міндетіқазақстандық үздік білім беру дәстүрлерін сақтау және олардың лингвистикалық санасын дамыту болып табылады, оның негізінде - мемлекеттік, ана тілі және шет тілдерін меңгеру.
Жалпы білім беретін мектептің оқу - тәрбие процесіне үш тілде оқытуды енгізу - бұл Қазақстан Республикасында білім беруді дамыту тұжырымдамасын іске асыру бағытында маңызды қадам.
Ағылшын бағыттағы бірқатар пәндерді ағылшын тілінде оқыту «100 қадам» Ұлт жоспарында көзделген, онда 79-қадам «Білім беру жүйесінде - жоғары мектеп пен жоғары оқу орындарында ағылшын тіліне кезең-кезеңмен көшу» делінген.
Ағылшын бағыты бойынша физика, химия, математика, информатика пәндерін ағылшын тілінде оқытуға кезең-кезеңмен көшу 2015 жылғы «Үш тілде білім беруді дамытудың 2015-2020 жылдарға арналған
Жол картасында көрсетілген. 2017-2018 оқу жылында ЖМБ пәндерін ағылшын тілінде пилоттық оқыту басталды. 2018-2019 оқу жылында жалғасты. 2019-2020 жылдары 10-11- сынып білім алушылары, олардың ата-аналарының қалауымен ЖМБ физика, хим, математика, информатика пәндері ағылшын тілінде оқытылады.
Сауалнама онлайн-режимінде өткізілді. Онлайн-сауалнаманың сұрақтары келесі категор дағы респонденттерге арналған:
- қазақ тілі пәні мұғалімдері;
- орыс тілі пәні мұғалімдері;
- физика пәні мұғалімдері;
- хим пәні мұғалімдері;
- математика пәні мұғалімдері;
- информатика пәні мұғалімдері.
Онлайн-сауалнамаға ЖМБ пәндерін ағылшын тілінде пилоттық режимде оқытатын 153 мектептің мұғалімдері қатысты
Бұл зерттеу шет тілдеріне үйретілген Әдістемедегі маңызды мәселелердің біріне арналған-бұл оқыту кезінде амалдар мен әдістерді таңдау.
Әдістердің классификациясы күрделі мәселе болып табылады, өйткені олардың атаулары әртүрлі белгілерге негізделген. Қазіргі жағдайда оқыту амалдарі мен амалдарін дамытуға көп көңіл бөлу керек . Амалдар мен амалдар оқытылды-оқу процесінің маңызды компоненттерінің бірі. Тиісті амалдар қолданылмаса, мұғалім жоспарлаған мақсаттар мен міндеттерді жүзеге асыру мүмкін емес. Әрбір мұғалім оқытылған процесте амалдар мен әдістерді дұрыс қолдана білуі керек .
Оқытылған заманауи техниканың жетекші бағыттарының бірі-қойылған мақсаттарға толық сәйкес келетін оқытылған әдістерді іздеу. Әдіс пен техниканы дұрыс таңдау мәселесі өте күрделі. Ол әсіресе жас және бастауыш мұғалімдерде жұмыс істеу кезінде әрқашан белгілі бір қиындықтар тудырды.
Зерттеу пәні- математикм сабағын ағылшын тілінде оқыту амалдарі мен амалдарі .
Мақсаты -математиканы шетелдік және отандық әдістемелерде дамыған әр түрлі амалдар мен әдістерді зерттеу, заманауи әдістерді анықтау.
Мақсатқа жету үшін келесі міндеттерді шешу қажет болды :
- осы мәселе бойынша оқытылған Әдістемеде бар зерттеу және қорытындылау
- математиканы шетелдік оқыту амалдарі мен амалдарінің мәнін ашу
- ең тиімді амалдар мен тәсілдерді анықтау
- математиканы шетелдік негізінде жаттығулар кешенін әзірлеу
Қойылған міндеттер келесі әдістерді қолдану арқылы шешілді:
- қарастырылып отырған мәселе бойынша әдебиеттерді талдау
- педагогикалық процесті бақылау
І Математикалық амалдарды ағылшын тілінде үйрету тәсілдері 1. 1 Математика шет тілін меңгеру құралы ретінде
Біздің елімізде ата-аналар да, оқушылар да математика мен шет тілі кез-келген типтегі мектептерде міндетті пәндер екенін біледі: жалпы білім беретін және мамандандырылған. Неліктен мен, ағылшын тілі мұғалімі, математиканы есіме түсірдім? Газеттерде жұмыс туралы жарияланды, телереклама шет тілін міндетті түрде білуге, компьютерде жұмыс істеуге және таңдаған салада кәсіби дайындыққа бағытталған.
"Жаңа мыңжылдықтар үшін білім" - бұл шет тілдерін білу. Енді сіз кейбір студенттердің екі, кейде үш шет тілін үйренетіндігімен ешкімді таң қалдырмайсыз. Бұл ата-аналардың бала кезінен гуманитарлық білім алуға бағытталған сирек кездесетін жағдайлары.
Біздің өлкеміздің кейбір бұрыштарында шет тілі үнемі естіледі (Новороссийск, Анапа, Туапсе, Сочи, Краснодар, Ейск) . Осы аудандарда орналасқан мектептерде шет тілін үйрену, басқа мәдениетпен танысу қажеттілігін түсіндірудің қажеті жоқ.
Егер статистикалық мәліметтерді талдайтын болсақ, Тихорецк қаласындағы мектеп түлектерінің көпшілігі техникалық жоғары оқу орындарына немесе оқу орындарына түседі, онда болашақ мамандықты игеру барысында Жоғары математика курсы оқытылады. Олардың ішінде: Краснодар мен Ростовтың техникалық және аграрлық университеттері. Қазіргі уақытта елге бір немесе бірнеше шет тілдерін жетік білетін жоғары білікті мамандар қажет. Ресейдің кез-келген бұрышында дәл ғылымдар саласында жақсы инженерлік және іргелі білім жүйесі қалыптасқан. Алайда, нақты және инженерлік ғылымдар саласындағы іргелі дайындықтың жоғары деңгейі мен шет тілін кәсіби меңгерудің төмен деңгейі арасында алшақтық бар екенін ашық мойындау керек. Қазіргі деңгейде Биотехнология дамыған, қоғамның интернет жүйесі арқылы ақпарат алмасуға деген қызығушылығының артуы шет тілін меңгерудің төмен деңгейіне жол бермейді. Мұндай ереже барлық саналы түрде меңгерілген. Кәдімгі зубрежка-утомительна. Оқушылардың ағылшын тілін үйренуге деген қызығушылығын арттыру үшін қандай амалдар мен педагогикалық технологияларды қолдану керек? Елде әртүрлі амалдар мен амалдар игеріліп, қолданылады, атап айтқанда, эмоционалды-семантикалық әдіс, л. Гегечкоридің қарқынды курсы, батыру әдісі, резервтік мүмкіндіктерді белсендіру әдісі, Берлицтің табиғи әдісі және т. б. оқытылды, алайда олардың тек мектептерде ғана емес, сонымен қатар университеттерде де жарамсыз болуының көптеген себептері бар. Олардың ішінде: мектептердің материалдық базасының жеткіліксіздігі, қосымша курстарға қаржыландырудың жеткіліксіздігі, оқушылардың шамадан тыс жүктелуіне байланысты қарқынды оқытудың мүмкін еместігі.
Бірақ шет тілінде оқытылған мәселеге басқаша қарауға болады. Мұндай тәжірибе біздің елімізде бар. "Тіл "үшін" тіл " емес, шет тілін оның қолданбалы тілі арқылы оқыту маңызды .
5-сыныптан бастап Оқушылар математиканың базалық деңгейін қалыптастырады. Х-ХІ сыныптарға оқушылар осы пән бойынша белгілі бір білім деңгейіне жетеді. Көптеген студенттер болашақ мамандыққа бейімділікті анықтайды. Көбінесе оқушылар шешім қабылдады: кім болу керек, әрі қарай қайда оқу керек. Дәл, инженерлік немесе экономикалық ғылымдарды таңдаған студенттер үшін факультативті сабақтар, шет тіліндегі математиканы оқу өткізілді.
Бұл қандай мақсат үйретілген ? Математика мен ағылшын тілін меңгерудегі бірлікке қол жеткізу, яғни ағылшын тіліндегі математикалық терминологияны меңгеру, ғылыми-техникалық және экономикалық сипаттағы материалдарды ағылшын тілінде дамыту, бұл болашақ кәсіби қызметте қажет. Мұндай сабақтарды мен, Тихорецкадағы № 6 гтмназияның ағылшын тілі мұғалімі ағылшын тілінде математиканың жеке бөлімдерін көрсете отырып өткіздім . Мен келесі қағидаларды ұстануға тырыстым:
1. Математика бөлімін түсіндіруде тек ағылшын тілін қолданды.
2. Негізгі оқу материалы түпнұсқа шетелдік көздерден алынды ("математика" " мәтін-Поберт Пауэлл, математика жетекшісі
Barton Borough School, Shropshire - design and illustrations - BPP (Letts Educational) Ltd. )
Әрине, мұндай "математика" сабақтарында бұрын зерттелген материалдар қолданылды: 9-сыныпта оқушыларға ағылшын тілінде квадрат теңдеулерді шешу түсіндірілді ( оқушылар 8-сыныпта оқиды. ) Бірақ студенттер ағылшын тілінде сөйлеуді шетелдік тілдік ортада болғандай естіді және ағылшын тілін ана тіліндегідей тез және еріксіз қолдану әдеті пайда болды.
Математика ғылымы дәл және ақыл-ой гимнастикасы екенін есте ұстай отырып, математика материалы түпнұсқа шетелдік көздерден алынды, студенттерге ағылшын тіліндегі математикалық терминдердің қысқаша және нақты тұжырымдалуына дағдыланды.
Сонымен бірге ол ескерді; әр тілдің өзіндік ерекшеліктері бар: идиомалық өрнектер мен терминдер, кейде математика саласында аударма әдісімен айту мүмкін емес, өйткені әртүрлі тілдерде сөздердің бір-біріне сәйкес келмеуі жоқ. Бұл жағдайда ағылшын тілінде математикалық ойлау қажет. Ағылшын тілін үйренуге осындай көзқараспен математикалық тұжырымдама мен ағылшын тілі арасында бөлінбейтін байланыс орнатылады.
Жинақталған тәжірибеден мен ағылшын тілінде оқытылған әдістерді қабылдамаймын деп қорытынды жасауға болады, ал математика ағылшын тілін меңгерудің құралы болған кезде оларды тек толықтырады. Бұл қол жеткізілген білім деңгейін бекітуге, студенттерді одан әрі қызықтыруға және басқа жоғары деңгейге өтуге мүмкіндік береді.
Әрине, біздің жалпы білім беретін мектептерде ағылшын тілі тереңдетусіз оқытылды, кейбір пәндер ағылшын тілінде оқытылмайды, бірақ мектеп бағдарламасына сәйкес біздің № 6 гимназияда математика мен ағылшын тілінің қажетті деңгейі қамтамасыз етіледі. Мұндай сабақтарды сәтті өткізу үшін математика мен ағылшын тілін меңгерудің жоғары деңгейі қажет. Оқушылар үшін қосымша лексиканы игеру үлкен қиындық тудырмайды. Математиканың осы бөлімдерімен таныс бола отырып, олар оңай түсіндіреді квадрат түбірлерді қалай табуға болады ағылшын тілінде теңестірілген, мысалы:
Мен "квадрат теңдеулерді графикалық түрде шешілді"тақырыбында интеграцияланған сабақтың әдістемелік дамуын ұсынамын.
Solving Equations Using Graphs.
Quadratics.
A quadratics equation is an equation of the form ax2 + bx + c = 0 with a ≠ 0.
You can solve an equation of this form by plotting the graph of y = ax2 + bx + c and finding the value of x when y = 0. This means finding the values of x where the graph crosses the x - axis.
Eg. Solve the equation x2 - x - 2 = 0 by drawing the graph of y = x2 - x - 2
First produce a table of results.
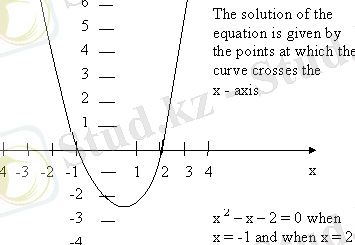
 Plot the points and join them with a smooth curve:
Plot the points and join them with a smooth curve:
And you have to check your results by substituting your solutions back into the equation.
Check: 22 - 2 - 2 =-2 = 0.
Where you can, solve the following equations by draning their graphs.
(One of the equations has no solutions)
a) x2 - 5x + 4 = 0 0 ≤ x ≤ 5
b) x2 - 3x + 2 = 0 -1 ≤ x ≤ 4
c) 2 + x - x2 = 0 -2 ≤ x ≤ 3
d) x2 - 4x + 4 = 0 -1 ≤ x ≤ 4
e) x2 + 3 = 0 -2 ≤ x ≤ 2
A quadratic equation has two solutions if the curve crosses the x - axis, it has one solution if the curve just touches the x - axis and it has no solution if the curve does not cross or touch the x - axis.
Another way to find the solutions of a quadratic equation is by drawing a curve and a straight line. The solutions are given by the points where the line crosses the curve.
E. g. A gardener wants to build a flower bed in her garden. She has 10 m of edging to construct a rectangular bed.
a) Find the maximum area of flower bed she can make with this edging.
b) If the gardener wants area of the flower bed to be 4. 5m2 what should the length be?
Draw a graph of area against length for the flower bed.
Cope and complete this table of values.
Copy and complete the graph.
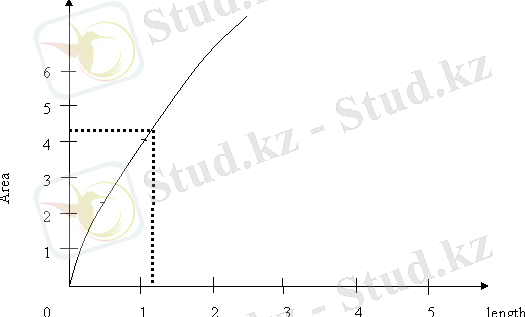
Let length = 1 width = w
We know 2(1+n) = 10
1 + w = 5
w = 5 - L
Let the area of the bed = A
A = Lw = 1(5-1)
So the equation of the curve is
A = 51- L2
a) From the graph, the maximum area is 6 . 25m2
b) Draw a horizontal line across the graph with the equation A = 4 . 5
This line crosses the curve at two points. At these points you draw a vertical line to the L - axis.
This gives you, two possible lengths for the flower bed.
To 1 decimal place, the lenthg is 1 . 2 m or 3 . 8 m
These points are the solutions of the equation 51 - 12 = 4 . 5
Remember Always check your answers are correct to 1 d. p.
Note: The accuracy of the answers depends on how carefully the graph is drawn.

 2. Draw the graph of y = x2(-3 = x = 3) and then use it to solve the following equations.
2. Draw the graph of y = x2(-3 = x = 3) and then use it to solve the following equations.
a) x2 = 4
b) x2 = 2x + 3 (Draw the line given by the equation) y = 2x + 3 and find where it crosser the curve.
c) x2 = - x
3. Draw the graphs of y = x2 + 2x - 4
(- 4 ≤ x ≤ 3) and y = x + 2 on the same pare of axes. Use the graph to solve the equation x2 + 2x - 4 = x + 2
Quadratic Equations.
You have already seen how to solve quadratic equations by drawing graphs and finding points intersection. This unit covers various algebraic methods for solving quadratic equations.
Factorisation
You already know how to factorise quadratic expressions into two bracket of the form (ax + b) (cx + d)
So. Given a quadratic equation you can write it in the form.
( ax + b) (cx +d) = 0
When two numbers multiply together to give zero then at least one of the numbers must itself equal zero.
 There fore (ax + b) = 0 or (cx + d) = 0 or both if (ax + b) = 0 then x = - ba
There fore (ax + b) = 0 or (cx + d) = 0 or both if (ax + b) = 0 then x = - ba


 and if (cx +d) = 0 then x = - dc so the solutions (roots) of quadratic equation are x = - ba and x = - dc
and if (cx +d) = 0 then x = - dc so the solutions (roots) of quadratic equation are x = - ba and x = - dc
E. g. Solve the equation 6x2 + 5x - 6 = 0 by factorizing.
First factorise 6x2 + 5x - 6
You need to find two factors, of 6 which combine with another two factor of 6 to give 5. Because the number term is negative you are looking for the difference to equal 5.
Hint: Start by trying the factors which are closes together.
The closests factors of 6 are 2 and 3.
Try the factor pairs (2, 3) and (2, 3) .
3 x 3 - 2 x 2 = 5 which gives the result you wait.
One factor pair gives the coefficients of x so start with.
(2x ) ( 3x )
The other factor pair goes at the ends of the brackets. To get 5 you need to multiply the 3`S together and the 2`S together so this tells you which brackets to put each number in.
(2x 3) (3x 2)
Because the number term is original expression is negative the signs in the brackets will be different. To get 5 you subtracted the 2 x 2 so the goes in front of the 2.
(2x+3) (3х- 2)
Check: (2x+3) (3x-2) = 6x2 -4x +9- 6 = 6x2 + 5x - 6.
So 6x2 + 5x - 6=(2x+3) (3x-2)
Putting (2x+3) (3x-2) =0.
gives (2x+3) =0 or (3x-2) =o

 So the solutions are x = - 32 and x = 23
So the solutions are x = - 32 and x = 23
Remember: Always check your answer multiplying the brackets.
Solve the following quadratics by factorizing:
a) 8x2 + 16x + 6 = 0. b) 9x2 + 27x + 20 = 0.
c) 6x2 - 40x -14 = 0.
Not all quadratics can be factorised into brackets with integer
(whole number) coefficients (eg. x2-7) so need an alternative method.
Hint: If a question ask you to solve a quadratic to a given number of decimal places then you cant do it by factorizing.
Completing the square.
One method winch works for all quadratic equations (unless the don`t have any solutions - see below) is completing the square. This is a way of getting x to appear only once in the equation so that you can then simply rearrange it to find the values of x.
E. g a) Sоlve the quadratic x2 - 7x -12 = 0 to 2 decimal places.
First get the terms involving x on one side and the number of the other.
x2 - 7x =12
Then write the expression on the left hand side (LHS) in the form of a square. To do this you divide the coefficient of x (the number in front of x ) by 2.
 (x - 72 ) 2
(x - 72 ) 2
 Expanding this bracket gives x2 - 7x+ 494
Expanding this bracket gives x2 - 7x+ 494
or x2 - 7x + 12 . 25
So by adding 12 . 25 to the LHS you can complete the square.
To preserve the equation you must also add 12 . 25 to the RHS.
x2 - 7x = 12
x2 - 7x + 12 . 25 = 12 + 12 . 25
(x - 3 . 5) 2 = 24 . 25

 Taking square roots,
Taking square roots,



 x - 3
.
5 = + 24
.
25
x - 3
.
5 = + 24
.
25

 x - 3
.
5 = + 24
.
25
x - 3
.
5 = + 24
.
25
To 2 decimal places the solutions are x = 8 . 42 and 1 . 42
b) Solve the quadratic 3x2 + 2x - 4 = 0.
to 2 decimal places.
First get all the terms involving x on the left hand side (LHS)
3x2 + 2x = 4.
Then divide through by the coefficient of x2.

 x2 + 23 x = + 43
x2 + 23 x = + 43
Divide the coefficient of x by 2 then square it and add to both sides.



 x2 + 23 x + 19 = 43 + 19
x2 + 23 x + 19 = 43 + 19
This can now be factorised

 (x += 139
(x += 139

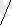 Taking the square root of both sides.
Taking the square root of both sides.



 x + 13 = + 139
x + 13 = + 139
To 2 decimal places the solutions are x = 0 . 87 and x = - 1 . 54
Solve the following equations to 2 decimal places by completing the square
a) x2 + 3x - 5 = 0 b) x2 - 2x - 34 = 0
The Formula
You can apply the same process of completing the square to the equation ax2 + bx + c = 0
(Try doing thing this yourself)
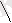

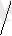 This gives the following formula for the solutions of a quadratic equation:
This gives the following formula for the solutions of a quadratic equation:

 -- b + b2 - 4 ac
-- b + b2 - 4 ac
E. g. Solve the quadratic 3x2 + 2x - 4 = 4
or to decimal places.
Comparing with ax2 + bx + c = 0 you have
a = 3 b = 2 c = - 4

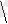
 Substituting the formula
Substituting the formula


-- 2 +x 3x - 4



-- 2 + 4 + 48




-- 2 + 52

To decimal places the roots are x = 0 . 87 and x = - 1 . 54
Solve the following quadratics to 2 decimal places using the formula
2x2 - 3x - 7 = 0 3x2 - 5x - 1 = 0
Note: You will usually be given the formula an exam.
Жоғарыда айтылғандардың бәрінен математика ағылшын тілін меңгеру құралы ретінде барлық студенттер үшін қолайлы емес деген қорытынды жасалады. Мен осындай топтарға математика мен шет тіліне қабілетті және қызығушылық танытатын студенттерді қатыстырдым. Жоғарыда айтылғандардың бәрі авторлық бағдарлама емес, сонымен қатар студенттердің қызығушылық танытуына ықпал ететін шет тілін меңгеруге көмектесетін практикалық тәжірибе.
Жүйелі көзқараспен, 1 - ші жылдың соңына қарай студенттер еркін, кідіріссіз, көрінетін күш-жігерсіз ағылшын тілінде зерттелген материалды, міндеттерді қоюды, олардың барысын шешеді .
Аударма қажеттілігі төмендейді: сандар әлемі бәріне түсінікті. Жадтың өзі қажетті сөздерді айтады және айтылады . Математикада оқушы қалай айту керектігін емес, айтылғанның мағынасына назар аударады. Бұл тіл артқы жағына өтіп, саналы түрде бақыланатын жағдай. Сөйлеу және сөйлеу дағдылары автоматизмге жеткізіледі.
Ең бастысы: математика бөлімдерін өз бетімше таңдау керек, оқушылар математиканы оқитын оқулықтардың авторына қарамастан, математиканың аспектілеріне әсер етпеймін. Бағдарламасын, әдістемесін оқытылған математика қалады мәні арнайы талқыланып, ортада жүргізілді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz