Модуль таңбасымен берілетін теңдеулерді оқытуға арналған үйірме бағдарламасын құру


Курстық жұмыс
Қазақстан Республикасы Білім және Ғылым министрлігі
Академик Е. А. Бөкетов атындағы Қарағанды университеті
Математика және ақпараттық технологиялар факультеті
Математиканы және информатиканы оқыту әдістемесі кафедрасы
КУРСТЫҚ ЖҰМЫС
Пәні: Сыныптан тыс жұмыс (факультативтік сабақ)
Тақырып: “Модуль таңбасымен берілген теңдеулер” үйірмесінің бағдарламасын құру
Орындаған: МиИ-419 топ студенті
Абдувалиева. У. М.
Тексерген: Ахманова Д. М.
Қарағанды, 2021
Мазмұны
КІРІСПЕ
І. МАТЕМАТИКАДА МОДУЛЬДІҢ ТЕОРИЯЛЫҚ МАҒЫНАСЫ
1. 1 Математикалық модуль және оның қасиеттері
1. 2 Математикалық модулдің басқа пәндермен байланысы
ІІ. МОДУЛЬ ТАҢБАСЫМЕН БЕРІЛГЕН ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ТАЛДАУ
2. 1 Модуль таңбасы бар теңдеулерді мен теңсіздіктерді шешу
2. 2 Модуль ішіндегі айнымалысы бар теңсіздіктерді шешу
ҚОРЫТЫНДЫ
ПАЙДАЛАНҒАН ӘДЕБІЕТТЕР
ҚОСЫМША
Түсінік және анықтама
Бұл тақырыпты кеңірек оқып үйрену үшін, маған қажет болатын қарапайым анықтамалар туралы түсінік келтіруді жөн санадым.
Теңдеу- бұл айнымалысы бар теңдік.
Модуль таңбасы бар теңдеу- айнымалысы модуль таңбасы немесе абсолют шама астында болатын теңдеу. Мысалы: x=1
Теңдеуді шешу- бұл барлық түбірді табу немесе түбірі жоқ екенін дәлелдеу.
Математикада модульдің әртүрлі мағынасы бар, мен өзімнің зерттеу жұмысымда тек бір мағынасын қарастырдым.
Модуль-санның абсолют шамасы, сандық түзуде санақ басынан берілген санға сәйкес нүктеге дейінгі қашықтық.
Кіріспе
Қазіргі заман математика ғылымының өте кең тараған кезеңі . Ал талапқа сай математикалық білім берудің басты шарты математикалық мəдениеттің деңгейін көтеру болып табылады.
Математикалық есептерді шешу, теоремаларды дəлелдеу оқушылардың ойын оятып, ойлау, есте сақтау қабілеттерін дамытуда, батыл қимылдар жасауға, шығармашылық ізденіске тəрбиелейді.
Ендеше оқушылардың математикаға дайындығын жан-жақты жетілдіру қазіргі аса маңызды міндеттердің бірі.
Бұл курстық жұмыста санның модулі туралы ұғым жəне оның қасиеттерін пайдаланып, модуль таңбасы бар теңдеулер мен теңсіздіктерді шешуді таңдап алдым. Себебі математикадан берілетін есептер ішінде модуль таңбасы бар теңдеулер мен теңсіздіктерді шешуге көптеп кездеседі. Бірақ бұл тақырыптың есептерін шешуге мектеп бағдарламасында сағат аз . Сондықтан модуль таңбасы бар теңдеулер мен теңсіздіктерді шешудегі оқушылардың білімдері саяз болғандықтан ондай есептерді шешуде қиындыққа кездеседі. курстық жұмыста есептердің мазмұны, оқулықтағы жəне ҰБТ - дағы есептер. Есептердің шығарылу жолдары алдымен əртүрлі тəсілдермен көрсетіліп, ал қалған есептерді оқушылардың өздерінің тиімді тəсілді таңдап алуына баса назар аударылады. Шешімдерді іздеудің математикалық методтарын, логикалық пайымдаулардың, математикалық модельдердің, адекваттылық мəселелерін оқушылар меңгеріп алуларына зор көңіл бөлінеді.
І. МАТЕМАТИКАДА МОДУЛЬДІҢ ТЕОРИЯЛЫҚ МАҒЫНАСЫ
- Математикалық модуль және оның қасиеттері
Тұрмыста кейбір шамалардың (ұзындықтың, массаның, температураның) өзгерістерінің сан мәні ғана жазылады. Өзен суы деңгейінің өзгерісі 20см. Мұнда өзен суының деңгейі 20см-ге жоғары көтерілді ме немесе 20 см-ге төмен түсті ме, оған назар аударылмайды. Демек берілген санның оң не теріс сан екені ескерілмейді. Тек өзен суының соңғы деңгейінің алғашқы деңгейінен айырмашылығы 20см, мұны математикада санның модулі деп атайды.
Жазылуы:20=20, -20=20
Оқылуы:20 немесе -20 санының модулі 20-ға тең.
Модуль - латынның modulus деген сөзі-«мөлшер»дегенді білдіреді. Кейбір жағдайда «модульдің» орнына абсолюттік шама деп те атайды. Модуль белгісін 1841 жылы неміс математигі Карл Вейерштрасс (1815-1897) енгізген. Бұл көп мағыналы сөз, математикамен қатар ол архитектурада, физикада, техникада, тағы басқа ғылымдар программасында кездеседі.
Теореманың дәлелдемесі
Анықтама : а санының модулі немесе а санының абсолют шамасы а-ға тең, егер а нольден үлкен немесе тең болса, -а-ға тең, егер а саны нольден кіші болса, яғни
a, егер а≥0
a=
-а, егер а<0
Анықтамадан кез келген нақты а саны үшін a≥0 екендігі шығады.
Теорема 1 . Кез келген а≠0 нақты санының абсолют шамасы а және -а сандарының үлкеніне тең болады.
Дәлелденуі
1. Егер а оң сан болса, онда -а теріс сан, яғни -а<0<a, бұдан -a<a.
Мысалы: 5 оң сан, -5 теріс сан және -5<0<5, бұдан -5<5.
Бұл жағдайда a=a, яғни a мәні а және -а сандарының үлкеніне тең болады.
2. Егер а теріс сан болса, онда -а оң сан болады және а<-а, яғни үлкен сан -а. Анықтама бойынша a=-a, бұл жағдайда да -а және а сандарының үлкені -а-ға тең болатыны шығады.
Салдар1. Теорема бойынша -a=a. Бұл жағдайда -a және a шамасы -а және а сандарының үлкеніне тең болады.
Салдар2. Кез келген нақты а саны үшін а ≤ a, -a ≤ a теңсіздіктері тура болады.
Екінші теңсіздікті (-а ≤ a ) -1-ге көбейтсек (бұл жағдайда теңсіздік таңбасы қарама-қарсы таңбаға өзгереді) а ≥-a теңсіздігі кез келген нақты а саны үшін тура болады. а≤a және а≥-a теңсіздіктерін біріктіріп
-a ≤ a ≤ a қос теңсіздігін аламыз.
Теорема2.
Кез келген нақты а санының абсолют шамасы а
2
санының арифметикалық квадрат түбіріне тең болады, яғни a=
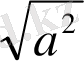 ;
;
Бұл жағдайда а≥0 болса, анықтама бойынша a=a, екінші жағынан а≥0,
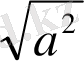 =a, яғни a=
=a, яғни a=
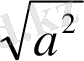
Егер а<0, онда a=-a және
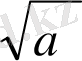 =-a бұл жағдайда a=
=-a бұл жағдайда a=
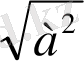
Бұл теореманы пайдаланып a ны
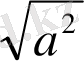 пен алмастыру арқылы кейбір теңдеулерді шешуге болады. Геометриялық мағынасы бойынша a координаталық түзудің бас нүктесінен a-ға сәйкес нүктеге дейінгі қашықтық. Егер а≠0 болса, онда координаталық түзуде а және -а сандарына сәйкес О нүктесінен бірдей қашықтықта екі нүкте болады, яғни a=-a. Егер а=0 болса, онда a координаталық түзуде О нүктесімен кескінделеді (1-сурет) .
пен алмастыру арқылы кейбір теңдеулерді шешуге болады. Геометриялық мағынасы бойынша a координаталық түзудің бас нүктесінен a-ға сәйкес нүктеге дейінгі қашықтық. Егер а≠0 болса, онда координаталық түзуде а және -а сандарына сәйкес О нүктесінен бірдей қашықтықта екі нүкте болады, яғни a=-a. Егер а=0 болса, онда a координаталық түзуде О нүктесімен кескінделеді (1-сурет) .
a a
1-сурет
1. 2 Математикалық модулдің басқа пәндермен байланысы
Геометриялық модуль туралы түсінік
Кез келген нақты сан белгілі бір сан түзуіндегі сәйкес нүктемен анықталуы мүмкін. Нөлден ерекшеленетін әрбір нүкте туралы оның нөлдің оң жағында немесе сол жағында жатқанын айтуға және нөлден осы нүктеге дейінгі қашықтықты өлшеуге болатындықтан, әрбір нақты санмен екі шаманы байланыстыруға болады: оның модулі және таңбасы. Егер белгілі бір санды көрсететін нүкте нөлдің оң жағында жатса, онда бұл санның таңбасы оң болып қабылданады. Егер бұл нүкте сол жақта жатса, онда белгі сәйкесінше теріс болады. Санның абсолютті мәні, бұл жағдайда, берілген санды көрсететін нүктеден нөлге дейінгі қашықтыққа тең.
Алгебралық модуль анықтамасы
Геометриялық тұрғыдан алғанда модульдің қызметі арасындағы қашықтық екенін біле отырып
Нақты сандар үшін де, күрделі сандар үшін де модульдің алгебралық қасиеттерін қарастырыңыз.
Нақты сандар үшін:
Модуль көлемі минус пен плюс шексіздікке дейін;
Нөлден плюс шексіздікке дейінгі мәндер диапазоны;
Модуль функциясы жұп (мұндай функцияның графигі аргумент белгісіне қатысты симметриялы) ;
Модуль функциясы нөлден басқа барлық аралықтарда дифференциялануы мүмкін. 0 нүктесінде функцияда үзіліс болады (осы нүктеде бастапқы функцияны бөлетін қисық тармақтарының жанамалары әртүрлі) .
Архитектурада-бұл өлшем бірлігі, архитектура құрылыстары үшін орнатылады және оның элементтер құрамының сәйкестігі үшін пайдаланылады.
Техникада-бұл термин, техниканың әрбір аймағында қолданылады, универсаль емес мән мен әртүрлі коэфициенттер және ұзындықтарын белгілеу үшін қолданылады.
Физикада-көлем қысымдылық модулі-материал ішінде нормаль күштің ұзындығына қатынастығы үшін қолданылады.
ІІ. МОДУЛЬ ТАҢБАСЫМЕН БЕРІЛГЕН ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ТАЛДАУ
2. 1 Модуль таңбасы бар теңдеулерді мен теңсіздіктерді шешу
Модуль таңбасымен берілген теңдеуді шешу үшін, біз санның модулінің анықтамасын және абсолют шама қасиеттерін негізге аламыз. Біз бірнеше мысалды әртүрлі тәсілмен шешуді қарастырып, олардың қайсысы тиімді екендігін көреміз.
Модуль белгісінің астында айнымалы шама болатын теңдеулерді шешудің мектеп программасындағы белгілі әдістері:
1. Модульдің геометриялық мағынасын пайдалану
2. Графиктік әдіс
3. Анықтама бойынша модульді ашу
Модуль таңбасымен берілген теңдеуді шешуде модульдің геометриялық мағынасын пайдалану.
x-a модулінің геометриялық мағынасы-координаталық түзуде х және а нүктелерінің арақашықтығы.
Мысал: x-1+x-2=1 модульдің геометриялық мағынасын пайдаланып теңдеуді шешейік. Ол үшін мына түрде талдау жасауға болады. Теңдеудің сол жақ бөлігінде х нүктесінен қашықтығы 1-ге және 2-ге тең болатын нүктелердің абсциссаларының қосындысын табамыз, яғни [1; 2] кесіндісіндегі барлық нүктелер берілген теңдеудің түбірі бола алады, ал ол кесіндіден тыс нүктелер абсциссалары теңдеу шешімі бола алмайды. Бұл жағдайда теңдеу шешімі [1; 2] кесіндісі болады.
Жауабы: x
 [1; 2]
[1; 2]
Мысал: x-1-x-2=1 теңдеуін шешейік.
Бұл теңдеудің сол жағындағы өрнек бойынша х нүктесінен қашықтығы 1 және 2 болатын нүктелердің абсциссаларының айырмасы 1-ге тең болатын аралық координаталық осьте 2 санының оң жағы, яғни берілген теңдеу шешімі бұл жағдайда кесінді емес, басы 2 санына тең нүкте болатын ох осінің оң бағытындағы сәуле болады.
Жауабы: x
 [2; ∞)
[2; ∞)
Бұл мысалдардан мынадай қорытынды жасадым.
x-a + x-b=b-a, егер b≥a
 a≤x≤b
a≤x≤b
x-a - x-b=b-a, егер b≥a
 x
x
Графиктік әдіс
Модуль таңбасымен берілген теңдеулерді шешудің бір әдісі -графиктік әдіс. Бұл әдіс функция графигін тұрғызуға негізделген. Егер берілген функциялар графиктері қиылысса, онда қиылысу нүктелерінің абсциссалары берілген теңдеу шешімі болады. Егер графиктер қиылыспаса, онда берілген теңдеу шешімі болмайды деген қорытындыға келеміз. Бұл әдіс модуль таңбасымен берілген теңдеулерді шешудің басқа әдістеріне қарағанда онша тиімді емес, себебі біріншіден, ол уақытты көп алады және үнемі рационалды емес, екіншіден график тұрғызғандағы нәтиже үнемі дәл болмайды.
Анықтама бойынша модульді ашу
Модуль таңбасымен берілген теңдеуді шешудің тағы бір әдісі-модуль анықтамасы бойынша модульді ашу, яғни кез келген f(х) функциясы үшін
f(х), егер f(х) ≥0 болса
f(х) =
-f(х), егер f(х) <0, болса
1-мысал. Теңдеуді шешу керек: 2x-5=1
Шешуі:1-ші тәсіл. a-b модулінің геометриялық мағынасы-түзудегі а мен b нүктелерінің арақашықтығы екенін ескерсек, жалпы жағдайда x-a=r түріндегі теңдеуді шешу үшін түзудегі а нүктеден r қашықтықта орналасқан екі нүктені тапса болғаны.
Біздің мысалымызда түзу бойында 5 санына сәйкес нүктеден 2х-ке сәйкес нүктеге дейінгі қашықтық 1-ге тең болатын екі нүкте бар, олар: 6; 4. Олай болса 2х=6 және 2х=4 теңдеулерін аламыз, бұдан х=3 және х=2. Жауабы:3 және 2.
4 5 6
Модулі бар теңдеулерді аралықтарға бөлу арқылы шешу
Аралықтарға бөлу әдісі бойынша теңдеулерді шешу үшін мына алгоритмді қолданған тиімді.
1) Модуль таңбасының ішіндегі өрнектерді нольге теңестіріп, теңдеуді шешу;
2) Теңдеулердің түбірлерін қолданып, сан түзуін аралықтарға бөлу;
3) Модуль анықтамасын ескеріп, әрбір жеке интервалда берілген теңдеуді шешу;
4) Теңдеудің шешімдерінің қарастырылып отырған аралыққа тиісті болатынын тексеру;
5) Тиісті түбірлерді берілген теңдеудің түбірі ретінде алу;
Берілген алгоритмнің қолданылуына мысалдар қарастырайық.
1-мысал. x-2+x-3+2x-8=9 теңдеуін шешейік. Шешуі: Алгоритм бойынша, алдымен
x-2=0 x=2
x-3=0 x=3
2x-8=0 теңдеулерін шешеміз. Сонда x=4
Табылған түбірлерді сан түзуінде белгілеп, (-∞; 2), [2; 3), [3; 4), [4; ∞) аралықтарын аламыз.
1 2 3 4 5, 5
2. 2 Модуль ішіндегі айнымалысы бар теңсіздіктерді шешу
Айнымалысы модуль таңбасымен берілген теңдеулерді модуль таңбасы бар теңдеулер деп атайды. Мысалы, =3, =2х+1, т. с. с. - модуль таңбасы бар теңдеулер.
Модуль таңбасы бар теңдеулерді шешудің бірнеше тәсілі бар. Оларды мысалдар арқылы қарастырайық.
1-мысал. =2 теңдеуінің түбірлерін табу керек.
1-тәсіл. (Геометриялық тәсіл) . өрнегінің геометриялық мағынасы - ол сан осіндегі х нүктесінен а нүктесіне дейінгі қашықтықты білдіреді. Онда =2 теңдеуінің геометриялық мағынасы х және 1 нүктелерінің ара қашықтығы 2-ге тең болатындығында. Олай болса, х =-1 немесе х =3 болуы керек.
Ж а у а б ы : х =-1; х =3.
1. 1-мысал
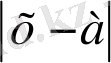 өрнегінің мәні
х
пен
а
сандарына сәйкес нүктелердің арақашықтығын білдіреді. Сонда
өрнегінің мәні
х
пен
а
сандарына сәйкес нүктелердің арақашықтығын білдіреді. Сонда
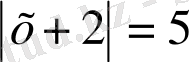 теңдеуінің геометриялық мағынасы
х
пен -2-ге сәйкес нүктелердің ара қашықтығы 5 болатындықтан
теңдеуінің геометриялық мағынасы
х
пен -2-ге сәйкес нүктелердің ара қашықтығы 5 болатындықтан
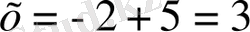 немесе
немесе

-5 5
-7 -2 3 х
Жауабы: x=3, x=-7
2-тәсіл. ( Квадраттау тәсілі ) . Берілген теңдеудің екі жақ бөлігі де оң болғандықтан, оны квадраттап, немесе квадрат теңдеуін аламыз. Оның түбірлері: =-1 және =3. Бұлар берілген есептің жауаптары.
Теңдеудің екі бөлігі де,
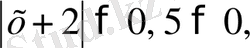 оң сандар болғандықтан, оларды квадраттап, берілген теңдеуге мәндес теңдеу аламыз. Сонда
оң сандар болғандықтан, оларды квадраттап, берілген теңдеуге мәндес теңдеу аламыз. Сонда
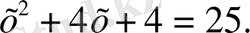 Бұдан
Бұдан
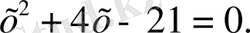 Виет теоремасын пайдаланып
, х=3,
x=-7
түбірлерін аламыз.
Виет теоремасын пайдаланып
, х=3,
x=-7
түбірлерін аламыз.
Жауабы: х=3, x=-7
2-мысал.
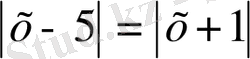 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі. Бұл теңдеуді де алдыңғы көрсетілген үш тәсілмен шешуге болады. Алайда, ең оңтайлысы-геометриялық тәсіл.
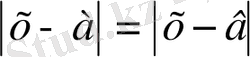 теңдігінің геометриялық мағынасы
х
нүктесі
а
мен
b
нүктелерінен бірдей қашықтықта жататынын көрсетеді, яғни [
a; b
] кесіндісінің дәл ортасы. Сонда
а<b
немесе
b<а
болғанда,
теңдігінің геометриялық мағынасы
х
нүктесі
а
мен
b
нүктелерінен бірдей қашықтықта жататынын көрсетеді, яғни [
a; b
] кесіндісінің дәл ортасы. Сонда
а<b
немесе
b<а
болғанда,
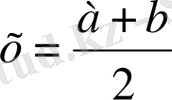

Демек, берілген теңдеудің шешімі
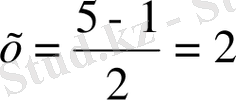

Жауабы: х=2
3-тәсіл. ( Анықтама тәсілі) . Анықтама бойынша
Осыдан, егер х -1 ≥ 0 болса, онда теңдігі және х-1<0 болса, онда теңдігі орындалады. Сондықтан сан осін х=1 нүктесі арқылы екі бөлікке бөлеміз: (- ∞; +∞) =(- ∞; 1) Осы бөліктің әрқайсысында берілген теңдеуді жеке шешу керек.
Егер х
 (-
болса, онда берілген теңдеуді -х+1
(-
болса, онда берілген теңдеуді -х+1
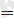 2 түрінде жазамыз. Осыдан х
2 түрінде жазамыз. Осыдан х
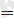 -1 болады.
-1 болады.
Егер х
болса, онда берілген теңдеуді х-1
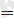 2 түрінде жазып, оның түбірін табамыз: х
2 түрінде жазып, оның түбірін табамыз: х
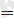 3.
3.
Ж а у а б ы : х
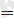 -1; х
-1; х
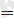 3.
3.
Осыдан,
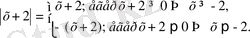
Яғни х≥-2 болғанда х+2=5, бұдан х =3, ал х<-2 болғанда -(х+2) =5, бұдан х=7.
Жауабы: х =3, x = -7.
2-мысал. теңдеуін шешу керек.
Шешуі. Мүнда болғандықтан, х-1 болуы керек. Сондықтан бұл теңдеуді мынадай екі жүйеге бөлеміз:
- {2х−5=х−1, х−1≥0, х≥2, 5, \left\{ \begin{array}{r} 2х - 5 = х - 1, \\ х - 1 \geq 0, \\ х \geq 2, 5, \end{array} \right. \2) {−2х+5=х−1, х−1≥0, х<2, 5, \left\{ \begin{array}{r} - 2х + 5 = х - 1, \\ х - 1 \geq 0, \\ х < 2, 5, \end{array} \right. \
Ж а у а б ы :
Модуль таңбасы бар теңсіздіктер
Модуль таңбасы бар теңсіздіктерді шешудің әртүрлі әдісі бар. Соның ішінде қолайлысы интервалдар әдісі.
1-мысал. теңсіздігін шешу керек.
Шешуі. өрнегін нөлге айналдыратын х-тің мәнін табамыз, яғни осыдан Сан түзуінде нүктесін белгілейміз.
- (−∞; 1] ( - \infty; \left. \ 1 \right\rbrackаралығын қарастырамыз. Бұл аралықта х-1 өрнегінің таңбасы теріс, яғни-(х−1) ≤3; −х+1≤3; −х≤2, х≥−2. -(х - 1) \leq 3; \ - х + 1 \leq 3; \ - х \leq 2, \ \ х \geq - 2. \Бұл аралықтағы шешім:[−2; 1] \lbrack - 2; 1\rbrack.
- (1; +∞) (1; + \infty) аралығын қарастырайық. Бұл аралықта х-1 өрнегінің таңбасы оң, яғних−1≤3; х≤4. х - 1 \leq 3; \ \ х \leq 4. Бұл аралықтағы шешім(1; 4] . (1; \left. \ 4 \right\rbrack.
Ж а у а б ы :
2-мысал. .
Шешуі. Мұнда
- (−∞; 1) ( - \infty; 1) аралығындах−1х - 1өрнегінің таңбасы теріс, ал2−х2 - хөрнегінің таңбасы оң, яғни
Бұл аралықтағы шешім
- [1; 2] \lbrack 1; 2\rbrackаралығындах−1+2−х>3+хх - 1 + 2 - х > 3 + х; ұқсас мүшелерді біріктерсекх<−2; х < - 2; яғни шешімі жоқ.
- (2; +∞) (2; + \infty) аралығындах−1−2+х>3+х; х - 1 - 2 + х > 3 + х\ ; ұқсас мүшелерді біріктерсекх>6. Бұларалықтағышешім(6; +∞) . х > 6. \ \ Бұл\ \ аралықтағы\ шешім\ (6; + \infty) .
- Ж а у а б ы :(−∞; 0) ∪(6; +∞) . ( - \infty; 0) \cup (6; + \infty) .
f(x) <g(x), түріндегі теңсіздіктерді шешу, мұндағы f(x), g(x) - қандай да бір функция
Берілген теңсіздіктердің шешімі:
және теңсіздіктер жүйелерін қанағаттандырады.
- Теңсіздікті шешіңдер:
-5х+6<0
Берілген теңсіздіктің шешімі мына теңсіздіктер жүйелерін қанағаттандырады
және
(х-2) (х-3)
+ - +
х
2 3
+ - +
х
-3 -2
сонда 2
Екінші жүйені шешеміз:
сонда -3
Жауабы: (-3; -2)
 (2; 3)
(2; 3)
Ескерту: Теңсіздікті жаңа айнымалы енгізу арқылы шешугі болады .
t=x, , .
f(x)
 түріндегі теңсіздікті шешу, мұндағы f(x), g(x) - қандай да бір функциялар
түріндегі теңсіздікті шешу, мұндағы f(x), g(x) - қандай да бір функциялар
Берілген теңсіздіктің шешімі:
теңсіздіктер жүйелерін қанағаттандырады.
g(x) болса, берілген теңсіздіктің шешімі жоқ.
- Теңсіздікті шешіңдер: х2−2х−3<3х−3х^{2} - 2х - 3 < 3х - 3
Мынадай теңсіздіктер жүйесін құрамыз:
2
х(х-5)
+ - + (х-2) (х+3)
Жауабы: (2; 5)
0 5 х
Екінші тәсіл : Теңсіздіктің шешімі мына жүйелерді қанағаттандыру керек:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz