Координаталар әдісін қарапайым есептерді шешуде қолдану

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СОЛТҮСТІК ҚАЗАҚСТАН ОБЛЫСТЫҚ БІЛІМ БАСҚАРМАСЫ

Манаш Қозыбаев атындағы Солтүстік Қазақстан университеті

Майсатаева Асем

ІІ курс студенті, М(о) -м-20к тобы

Олимпиадалық есептерді

векторлы - координаталық тәсіл

арқылы шешу

Петропавл, 2021

МАЗМҰНЫ

1. Кіріспе . . . 2

2. Жалпы теориялық ақпарат ……. . . 3

3. Координаталар әдісін қарапайым есептерді шешуде қолдану . . . . 4

4. Олимпиадалық есептерді векторлық-координаталық әдістермен шешу … 5

5. Қорытынды . . . 10

6. Пайдаланылған әдебиеттер тізімі . . . 11

КІРІСПЕ

Есептерді шешудің векторлық-координаталық әдісі әзірше ең күшті және дұрыс көзқараспен математикалық, физикалық, астрономиялық және техникалық есептердің барлық түрлерін іс жүзінде шешуге мүмкіндік береді. Сонымен қатар, мектеп бағдарламасында координаталар әдісі өте шектеулі және толық емес қолданылады. Біздің жұмысымызда біз стереометриялық есептердің қалай шешілетінін көрсету міндетін қойдық, , яғни мәселені үш өлшемді координаталар жүйесінде қарастырамыз.

Сонымен, бұл жұмыстың мақсаттары:

Мектептің геометрия курсында оқытылатын негізгі формулаларды және қосымша материалды пайдалана отырып, әдістеменің мазмұнын ашу;
Қарапайым есептер бойынша әдістің қолданылуын көрсету;
Векторлық-координаталық әдісті қолданып, күрделі стереометриялық есептерді шығару, салыстыру және оның артықшылықтарын көрсету.

Жұмыстың өзектілігі мынада: бұл әдіс олимпиадалық есептерді және С бөлімінің бірыңғай мемлекеттік емтихан тапсырмаларын сәтті шешуге мүмкіндік береді.

Жалпы теориялық мәліметтер.

Координаталар әдісінің негізгі формулалары.

Геометрияда есептерді шешудің әртүрлі әдістері қолданылады - бұл синтетикалық (таза геометриялық) әдіс, түрлендіру әдісі, векторлық әдіс, координаталық әдіс және т. б. Олардың мектепте әртүрлі қызметтері бар. Негізгі әдіс синтетикалық болып саналады, ал басқаларының ішінде координаттар әдісі ең жоғары орынды алады.

Геометрияның дамуында алгебраны геометриялық фигуралардың қасиеттерін зерттеуге қолдану маңызды рөл атқарды, ол дербес ғылым - аналитикалық геометрияға айналды.

Аналитикалық геометрияның пайда болуы оның негізгі әдісі болып табылатын координаталар әдісінің ашылуымен байланысты.

Геометрия курсында координаталар әдісін оқудың келесі мақсаттарын бөліп көрсетейік:

- геометриялық есептерді шығаруда алгебралық аппаратты қолдана білуді дамыту, соның негізінде алгебра мен геометрияның тығыз байланысын көрсету.

- есептеу және графика мәдениетін дамыту

-есептерді шешудің тиімді жолдарын көрсету және теоремаларды дәлелдеу.

Координаталық әдісті сәтті қолдану үшін есеп шартын координат тіліне аударып, содан кейін қажетті алгебралық түрлендірулерді орындап, теңдеулер жүйесін шешіп, кері ауысуды жүзеге асыра білу керек, яғни алынған нәтижені геометриялық интерпретациялау. Есепті шешу көмекші құрылыстарды орындауды қажет етпейді және табиғи түрде алгебра ережелерін қолдануды азайтады.

Бірақ мектеп тәжірибесінде координат әдісі өте сирек қолданылады. Әдістің кемшіліктері де бар. Қарапайым координаталық формуланың қарапайым геометриялық фактіге сәйкес келмейтіндігі, алгебралық түрлендірулердің қолайсыздығы және нәтижесінде алынған алгебралық тәуелділіктерді кейде геометриялық тұрғыдан түсіндіру қиынға соғатыны есептің шешімін жиі қиындатады. Осыған байланысты мәселені координаталық әдіспен шешу кезінде координаталар жүйесін дұрыс таңдаудың үлкен маңызы бар екенін атап өткен жөн. Бастауыш пен координат осьтері бұл пішінге ең табиғи жолмен бекітілуі керек. Әдетте, координат осі ретінде есеп нұсқауында көрсетілген түзу сызықтар және фигураның симметрия осьтері, егер бар болса, таңдалады .

Координаталық әдістің есептерді шешу әдісі ретіндегі мәні мынада: фигураларды теңдеулермен қою және әртүрлі геометриялық қатынастарды координаталар арқылы өрнектеу арқылы геометриялық есепті алгебра арқылы шешуге болады. Керісінше, координаттарды пайдалана отырып, алгебралық және аналитикалық қатынастарды және фактілерді геометриялық түрде түсіндіруге болады және осылайша геометрияны алгебралық есептерді шешуге қолдануға болады .

Координаттар әдісі жалпы әдіс болып табылады. Ол алгебра мен геометрия арасындағы тығыз байланысты қамтамасыз етеді, олар біріктірілген кезде олар бөлек қалса бере алмайтын «бай жемістер» береді.

Мектептегі геометрия курсына келетін болсақ, кейбір жағдайларда координаттар әдісі таза геометриялық әдістерге қарағанда дәлелдеулерді құруға және көптеген есептерді ұтымды, әдемі шешуге мүмкіндік береді деп айта аламыз. Координаталар әдісі бір геометриялық күрделілікпен байланысты. Бір тапсырма координаттар жүйесінің бір немесе басқа таңдауына байланысты басқа аналитикалық презентацияны алады. Және жеткілікті тәжірибе ғана координаттар жүйесін ең орынды таңдауға мүмкіндік береді .

Алгебралық және геометриялық есептерді координаталар әдісімен шешу үшін 3 кезеңді орындау қажет:

1) есепті координаттық (аналитикалық) тілге аудару;

2) аналитикалық өрнекті түрлендіру;

3) кері аударма, яғни координаттық тілден мәселе тұжырымдалатын тілге аудару

Мысал ретінде алгебралық және геометриялық есепті қарастырып, координаталық әдіс арқылы шешу кезінде осы 3 кезеңнің орындалуын суреттеңіз.

Кеңістікте OXYZ координаталық жүйесі енгізілсе, кеңістіктегі әрбір нүктеге (x, y, z) координаталары тағайындалады.

M ₁ (x ₁ ; y ₁ ; z ₁ ) және M ₂ (x ₂ ; y ₂ ; z ₂ ) нүктелерінің арасындағы кесіндінің ортаңғы нүктесінің координаттары бар және төмендегідей формуласы бойынша табылады:

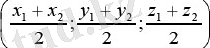
M ₁ (x ₁ ; y ₁ ; z ₁ ) және M ₂ (x ₂ ; y ₂ ; z ₂ ) нүктелерінің арасындағы қашықтық:

М ₁ М ₂ =

\[\sqrt{(x_{2}-\ x_{1})^{2}+(y_{2}-\ y_{1})^{2}+(z_{2}-z_{1})^{2}}\]

(x; y; z) нүктелер жиыны теңдеуді қанағаттандыратын:

(x-x ₀ ) ² + (y-y ₀ ) ² + (z-z ₀ ) ² = R ² - центрі (x ₀ , y ₀ , z ₀ ) және радиусы R болатын шар;

(x, y, z) нүктелер жиыны

ax + by + cz + d = 0 (a, b, c және d - нақты сандар) - жазықтық теңдеуі.

(x ₀ , y ₀ , z ₀ ) нүктесінен α жазықтығына дейінгі қашықтық, оның теңдеуі мына түрге ие: ax + by + cz + d = 0, 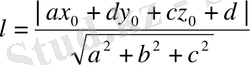тең.

Түзулер арасындағы бұрыштың косинусы, осы формула бойынша есептеледі.

cosφ =

\[\frac{\mid x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}\mid}{\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}\times{\sqrt{x_{2}^{2}+y_{2}^{2}}}}\]

Координаталар әдісін қарапайым есептерді шешуде қолдану

1. x-3y-2z + 5 = 0 теңдеуімен берілген А нүктесінен (-1, 3, 0) α жазықтығына дейінгі қашықтықты табыңыз.

Шешімі:

\[l=\frac{\left|-\,1-3\times3\times-\,2\lambda-5\right|}{\sqrt{1+2^{2}+3^{2}}}=\frac{\left|\,5\,\right|}{\sqrt{14}}=\frac{5}{\sqrt{14}}\]

2. Бастапқы А (0, 0, 0) нүктеден 2х + 3у-6з + 14 = 0 жазықтыққа дейінгі қашықтықты есептеңдер.

Шешімі : l =

\[\frac{|2\times\!0+3\times\!0-6\infty\!+\!14|}{\sqrt{2^{2}+3^{2}+6^{2}}}=\frac{|14|}{7}=2\]

А нүктесінен қашықтықты табу керек (0, 0, 0) . Формула бойынша аламыз:

3 . 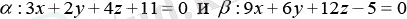теңдеулермен берілген α және β жазықтықтарының арасындағы сәйкесінше қашықтықты есептеңдер.

Шешім. Екінші теңдеудің екі жағын 3-ке бөлсек,

3х+2у+4z=5/12 теңдеуін аламыз.

Демек, жазықтықтар параллель.

β жазықтығына жататын кез келген А (x0, y0, z0) нүктесін алайық: мысалы,

x ₀ = 0, y ₀ = 0, содан кейін z ₀ = 5/12.

α және β жазықтықтарының арақашықтығы координаталары (0; 0; 5/12) нүктеден α жазықтығына дейінгі қашықтыққа тең екенін түсіну оңай:

l $= \frac{3 \bullet 0 + 2 \bullet 0 + 4 \bullet \frac{5}{12} + 11}{\sqrt{3^{2} + 2^{2} + 4^{2}}} = \frac{38}{3\sqrt{29}}$

ОЛИМПИАДАЛЫҚ ЕСЕПТЕРДІ ВЕКТОРЛЫҚ-КООРДИНАТАЛЫҚ ӘДІСТЕРМЕН ШЕШУ

КЛЕКОВКИН (105-106 бб)

4. 3. 1. 12. Қабырғасы 1-ге тең 𝐴𝐵𝐶𝐷𝐴 ₁ 𝐵 ₁ 𝐶 ₁ 𝐷 ₁ кубы берілген. 𝐴 төбесі, 𝐴 ₁ 𝐵 ₁ 𝐶 ₁ 𝐷 ₁ жағының ортасы және 𝐶𝐷 мен 𝐵𝐵 ₁ бүйірлерінің ортасы арқылы өтетін сфераның радиусын табыңыз.

Шешімі:

М - нүктесі СD қырының ортасы, N - ВВ ₁ қырының, ал L нүктесі 𝐴 ₁ 𝐵 ₁ 𝐶 ₁ 𝐷 ₁ жағының центрі болсын (1 - сурет) . $\overrightarrow{CD} = \overrightarrow{a}, \ \overrightarrow{DC} = \overrightarrow{b};$

$\overrightarrow{DD_{1}} = \overrightarrow{c}\$ векторларын базистік векторлары деп есептейік.

Онда $\overrightarrow{a}$ = $\overrightarrow{b}$ = $\overrightarrow{c}$ = 1, $\overrightarrow{a}\overrightarrow{b} = \overrightarrow{a}\overrightarrow{c} = \overrightarrow{b}\overrightarrow{c} = 0\$ және $\overrightarrow{DM} = 0. 5\overrightarrow{b}. \$

$\overrightarrow{DN} = \overrightarrow{DB} + \overrightarrow{BN} = \left( \overrightarrow{DA} + \overrightarrow{DC} \right) + 0. 5\overrightarrow{BB_{1}} = \overrightarrow{a} + \overrightarrow{b} + 0. 5\overrightarrow{c}$ ,

$C:\Users\77473\Pictures\Screenshots\Снимок экрана (168).png$ $\overrightarrow{DL} = \overrightarrow{DD_{1}} + \overrightarrow{D_{1}L} = \overrightarrow{c}$ +0. 5( $\overrightarrow{a} + \overrightarrow{b}$ ) .

Егер $\overrightarrow{DO} = x\overrightarrow{a} + y\overrightarrow{b}$ +z $\overrightarrow{c}$ - центрі О нүктесі болатын сфераның радиус векторы.

Онда $\overrightarrow{OA}$ = $\overrightarrow{OM}$ = $\overrightarrow{ON}$ = $\overrightarrow{OL}$ немесе

$\overrightarrow{OA}$ ² = $\overrightarrow{OM}$ ² = $\overrightarrow{ON}$ ² = $\overrightarrow{OL}$

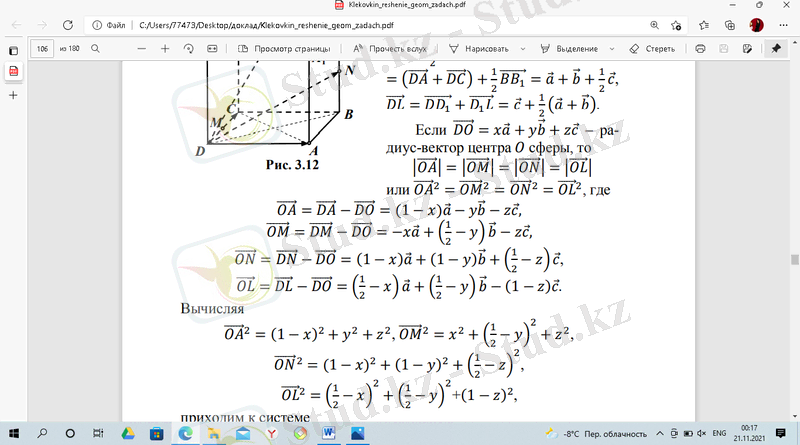
Есептей келе,

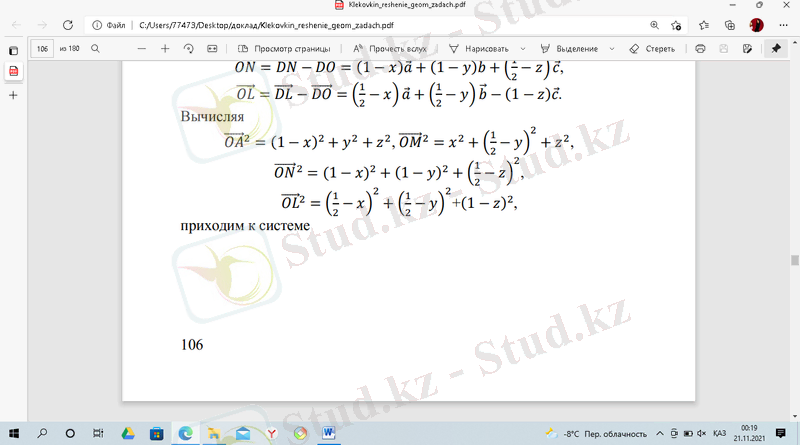
$C:\Users\77473\Pictures\Screenshots\Снимок экрана (170).png$

Осы жүйеге келеміз.

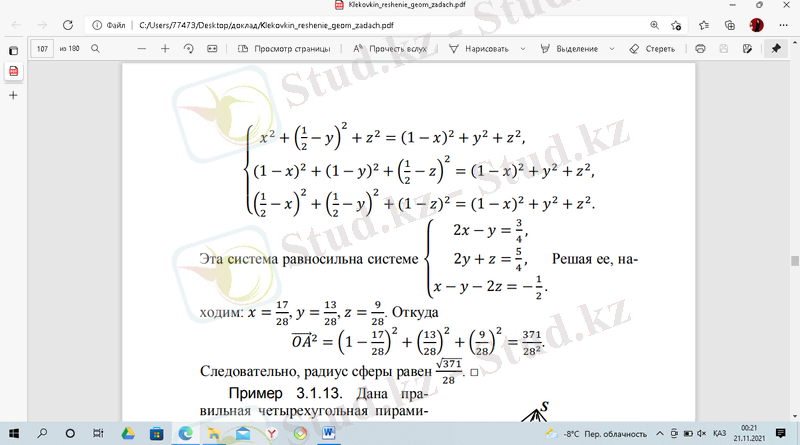
Ықшамдасақ,

Осыдан белгісіз айнымалыларды анықтасақ,

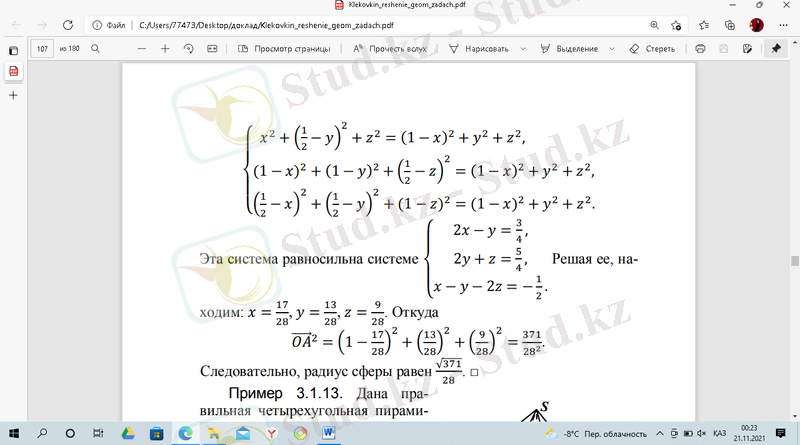шығады.

Демек,

Осыдан сфераның радиусы: R = $\frac{\sqrt{371}}{28}$ -ге тең екені шығады.

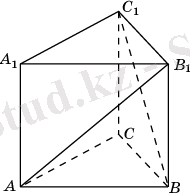
5. Дұрыс үшбұрышты ABCA ₁ B ₁ C ₁ призмада, барлық қырлары 1-ге тең екені белгілі. AB ₁ және BC ₁ векторларының арасындағы бұрышты табыңыз.

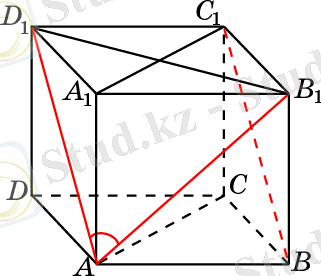
Ең алдымен берілген призманы төртбұрышты призмаға дейін толықтырайық. AD ₁ қабырғасын BC ₁ - ге параллель болатындай етіп жүргіземіз. Ізделінді бұрыш B ₁ AD ₁ бұрышының шамасына тең болады. AB ₁ D ₁ үшбұрышында (Пифагор теоремасы бойынша) _: АВ ₁ = АD ₁ = $\sqrt{2\ \ }$ , B ₁ D ₁ = $\sqrt{3\ }$ . Косинустар теоремасы бойынша cosφ = $\frac{1}{4}$ . φ =arccos $\frac{1}{4}$ .

Жауабы: φ =arccos $\frac{\mathbf{1}}{\mathbf{4}}$ .

А нүктесі координаталардың бас нүктесі болатындай призмамызды кеңістіктегі координалар жүйесіне саламыз . А, В ₁ , С ₁ және В төбелері келесідей координаталарға ие:

А(0, 0, 0), В ₁ (0, 1, 1), В(0, 1, 0), С ₁ ( $\frac{\sqrt{3}}{2}$ , $\frac{1}{2}$ , 1) .

Демек біз АВ ₁ және ВС ₁ векторларының координаталарын таба аламыз.

АВ ₁ (0, 1, 1), ВС ₁ ( $\frac{\sqrt{3}}{2}$ , $- \frac{1}{2}$ , 1) .

АВ ₁ және ВС ₁ векторлары АВ ₁ және ВС ₁ векторларының бағыттауыш векторлары болып табылады:

cosφ=

\[\frac{\mid x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}\mid}{\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2}}\times{\sqrt{x_{2}^{2}+y_{2}^{2}}}}\]

cosφ =

\[\frac{|0\times_{2}^{\sqrt{3}}+1\times(-\frac{1}{2})+1\times|}{\sqrt{2}\times\sqrt{\frac{3}{4}+\frac{1}{4}+1}}=\frac{1}{2}=\frac{1}{4}\]

Жауабы: φ =arccos $\frac{\mathbf{1}}{\mathbf{4}}$ .

6. ABCDA ₁ B ₁ C ₁ D ₁ бірлік кубында A нүктесінен BDC ₁ жазықтығына дейінгі арақашықтықты табыңыз:

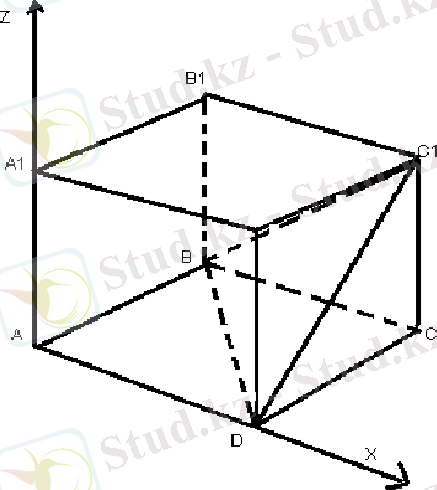
$C:\Documents and Settings\Администратор\Рабочий стол\Безымянный.bmp$

В(0; 1; 0), D(1; 0; 0) және С(1; 1; 1) нүктелері арқылы өтетін жазықтықтың теңдеуін жазайық. Ол үшін

Ax + By + Cz + D = 0. $\left\{ \begin{array}{r} B + D = 0 \\ A + D = 0\ \\ A + B + C + D = 0 \end{array} \right. \$ немесе $\left\{ \begin{array}{r} B = \ - D \\ A = \ - D \\ C = D \end{array} \right. \$

Осыдан -Dx - Dy + Dz + D = 0 немесе х + у - z - 1 = 0 шығады.

Формула бойынша A(0; 0; 0) нүктесінен BDC ₁ жазықтығына дейінгі арақашықтықты табамыз:

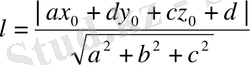
l = $\ \frac{1 \bullet 0 + 1 \bullet 0 - 1 \bullet 0 - 1}{\sqrt{1 + 1 + 1}}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$

Жауабы: $\frac{\sqrt{\mathbf{3}}}{\mathbf{3}}\mathbf{. \ }$

Есептерді шешудің екі әдісін талдай отырып, векторлық-координаталық әдіс қарапайымырақ деген қорытынды жасауға болады. Біз бұны алгоритмдік деп айта аламыз және бұл емтихандарда уақытты үнемдейді, ал бұл маңызды.

Келесі кезекте тек векторлық-координаталық әдіспен шешілген, геометриялық әдісті біз таппаған есепті ұсынғымыз келеді. Бұл векторлық-координаталық әдіс әмбебап екенін тағы да растайды.

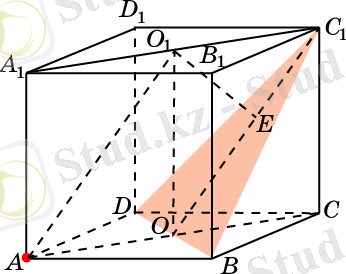
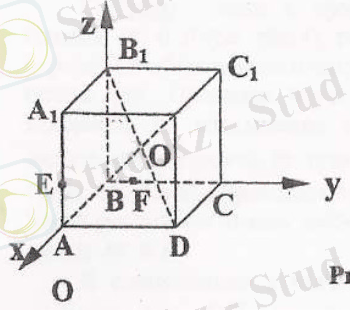
7. ABCDA ₁ B ₁ C ₁ D ₁ бірлік куб берілген. АА ₁ қырынан Е нүктесі, AE = $\frac{1}{3}$ болатындай етіп алынған. ВС қырынан F нүктесі, BF = $\frac{1}{4}$ болатындай етіп алынған. Кубтың центрі, Е және F нүктелері арқылы α жазықтығы ж. ргізілген. В ₁ төбесінен α жазықтығына дейінгі арақашықтықты табыңыз.

Шешімі:

В - координаталар бас нүктесі болсын. Онда Е(1, 0, $\frac{1}{3}$ ), F(0, $\frac{1}{4}$ , 0), В ₁ (0, 0, 1), О( $\frac{1}{2}$ , $\ \frac{1}{2}$ , $\ \frac{1}{2}$ ) . α жазықтығының жалпы теңдеуін анықтайық:

Ах + Ву + Сz + D = 0.

$C:\Documents and Settings\Ольга Алексеевна\Рабочий стол\Яркова\22.jpg$

α жазықтығы координаталардың бас нүктесі арқылы өтпегендіктен, D ≠ 0 демек теңдеуді D- ға бөлуге болады.

Келесідей теңдеу аламыз:

$\frac{A}{D}$ x $+ \ \frac{B}{D}y + \ \frac{C}{D}z + 1 = 0$ немесе ax + by + cz + 1= 0. (2)

Белгісіз a, b, c коэффициенттерін анықтау үшін (2) теңдеуге осы теңдеуді қанағаттандыратын үш E, F және O нүктелерінің координаталарын қоямыз (бұл нүктелер α жазықтығында жатыр) .

а∙1+b∙0+c∙ $\frac{1}{3}$ +1=0

а∙0+b∙ $\frac{1}{4}$ +c∙0+1=0

а∙ $\frac{1}{2}$ +b∙ $\frac{1}{2}$ +c∙ $\frac{1}{2}$ +1=0 Осыдан а = - $\frac{5}{2}$ , b = -4, c = $\frac{9}{2}$ табамыз.