Мектеп математика курсындағы тригонометриялық теңсіздіктер мен олардың жүйелерін шешуді оқыту әдістемесі


МЕКТЕП МАТЕМАТИКА КУРСЫНДАҒЫ ТРИГОНОМЕТРИЯЛЫҚ ТЕҢСІЗДІКТЕР МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІН ШЕШУДІ ОҚЫТУ ӘДІСТЕМЕСІ
МАЗМҰНЫ:
КІРІСПЕ
1. МАТЕМАТИКА КУРСЫНДАҒЫ ТЕҢСІЗДІКТЕР МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІ
1. 1 Мектеп курсындағы тригонометриялық теңсіздіктердің оқыту әдістемесінің теориялық негіздері
1. 2 Математика курсындағы теңсіздіктер мен теңсіздіктер жүйесінің түрлері
2. МАТЕМАТИКА КУРСЫНДАҒЫ ТРИГОНОМЕТРИЯЛЫҚ ТЕҢСІЗДІКТЕР МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІН ШЕШУДІ ОҚЫТУ ӘДІСТЕМЕСІ
2. 1 Қарапайым тригонометриялық теңсіздіктер мен теңсіздіктер жүйесін шешу әдістері
2. 2 Тригонометриялық теңсіздіктерді шешу жолдарын құру әдістемесі
2. 3 Педагогикалық эксперимент
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
КІРІСПЕ
Қазақстан Республикасы білім және ғылым министрлігінің нұсқалығына сәйкес, егер біз Қазақстан экономикасын, мәдениетін дамытып, жоғары дамыған елдердің қатарына жеткіземіз десек, онда бірінші орында білімді дамытуға тиіспіз. Ол үшін Қазақстанды болашақта өрге жетелейтін білікті мамандар даярлап, Отанына адал қызмет ететін азамат тәрбиелеп шығаруымыз керек. Қазіргі кезде осы мақсаттарды жүзеге асыру үшін жалпы білім беретін орындарға қойылған талаптар қатаңдалып, күннен күнге өсуде. Соның ішінде мектеп курсындағы гуманитарлық пәндер арасында математиканы оқыту үлкен іскерлікті қажет етеді. Мектепте математиканы оқыту - онымен тығыз байланыста жүретін пәндерді меңгеруге, күнделікті тұрмысқа қажетті біліктілік пен дағдыны қалыптастыруға және математиканы тереңдетіп оқытуға тиіс. Математиканы тереңдетіп оқыту - оқушының математикаға тұрақты қызығушылығын тудырып, олардың математикалық қабілеттілігін дер кезінде анықтап, дамуына ықпал етеді де жоғарғы оқу орнына түсуге дайындық мәселелерін шешеді. Оқушылардың математикалық даму әрежесі олардың есеп шығару қабілеттілігінен көрінеді. Кез - келген қиын есепті шығару оқушылардың үлкен еңбекті талап етеді. Мұғалімнің міндеті баланың бойындағы қасиеттерді ояту болып табылады.
Ол үшін мұғалімнің үздіксіз ізденуін, әдістемелік - теориялық білімін жүйелі көтеріп отыруын, терең толғауын, оқушылардың психологиясын зерттеп, тақырып ерекшелігін жете талдай білуін қажет етеді. Әсіресе бұл талаптар жоғары сыныптарда күшейе түседі. Соның ішінде 10 - сыныпта оқытылатын тригонометрия тақырыбының өзі үлкен бір тарау болып келеді. Тригонометриялық функциялар негізгі үш параграфтан тұрады. Соның ішінде біз тригонометриялық теңдеулер, теңсіздіктер және олардың жүйелерін шешу әдістерін қарастырамыз. Бұлардың ішіндегі тригонометриялық теңдеулер, теңсіздіктер тақырыбы өте күрделі. Оқушылар тригонометриялық теңдеулер мен теңсіздіктерді шешкенде үлкен қиындықтарға кездеседі. Сол себепті де мен өзімнің курстық жұмысымның тақырыбын Тригонометриялық теңдеуле теңсіздіктер және олардың жүйелерін шешу жолдары деген тақырыпқа арнадым. Курстық жұмысымды жазу барысында мынандай мақсат, міндеттер қойдым.
Мақсаты:
Жалпы тригонометриялық теңдеулердің, теңсіздіктердің түрлерін және олардың шешу жолдарын ашып көрсету.
Міндеті:
1. Тригонометриялық теңдеулердің, теңсіздіктердің шешу жолдарын көрсету. 2. Тригонометриялық теңдеулерді және теңсіздіктерді шешкенде ыңғайлы әрі оңай жолын таңдауға үйрету.
1. МАТЕМАТИКА КУРСЫНДАҒЫ ТЕҢСІЗДІКТЕР МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІ
1. 1 Мектеп курсындағы тригонометриялық теңсіздіктердің оқыту әдістемесінің теориялық негіздері
Анықтама . Құрамында белгісіз айнымалыға тәуелді тригонометриялық теңдеулер деп атайды.
Тригонометриялық теңдеулерді шешуді негізінен мынадай қарапайым тригонометриялық теңдеулерге келтіріп алып шешеді:
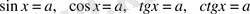 . Енді осы теңдеулерді шешу тәсілдерін қарастырайық.
. Енді осы теңдеулерді шешу тәсілдерін қарастырайық.
- теңдеуі. Егерболса, онда бұл теңдеудің екі шешімі бар:жәнеАлболғандықтан, бұл шешімдерді сәйкесжәненемесе оларды біріктіріп, түрінде жазуға болады. Мұндаболатынын ескерсек, онда берілген теңдеудің шешімін
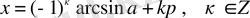 (1)
(1)
түрінде жазамыз. Егер
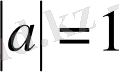 немесе
немесе
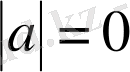 болса, онда (1) формуладан төмендегідей дербес жағдайлардағы формулаларды аламыз:
болса, онда (1) формуладан төмендегідей дербес жағдайлардағы формулаларды аламыз:
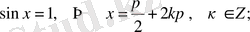
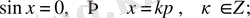 (2)
(2)
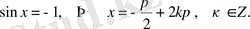
- теңдеуі. Оның шешімдері
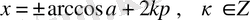 (3)
(3)
түрінде жазылады. Мұнда көрсетілгендей етіп дәлелдеуге болады. Формуланың дербес жағдайлары (
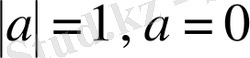 ) :
) :
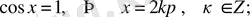 (4)
(4)
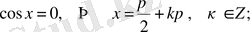
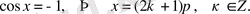
- теңдеуінің шешімдері
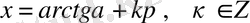
- теңдеуінің шешімдері
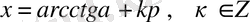
- мысал. теңдеуін шешу қажет.
Шешуі . Берілген теңдеуді 2-ге бөліп, оны
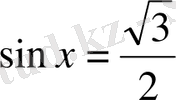 түрінде жазамыз. Онда (1) формула бойынша
түрінде жазамыз. Онда (1) формула бойынша
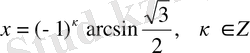 болады. Ал
болады. Ал
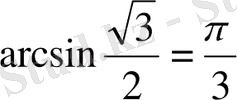
екенін ескерсек, онда берілген теңдеуінің шешімі
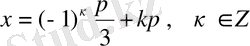 түрінде жазылады.
түрінде жазылады.
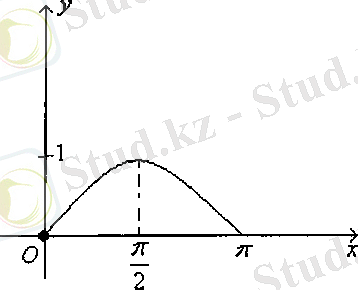
Ең бірінші әрбір тригонометриялық функциялардың графигін салуға тоқталайық.
1
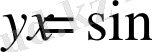 функциясын қарастырамыз. Функцияның:
функциясын қарастырамыз. Функцияның:
1) анықталу облысы
барлық нақты сандар жиыны, яғни

2) мәндер жиыны
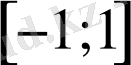 кесіндісі, яғни
кесіндісі, яғни

3)
 , функция периодты, оның ең кіші оң периоды 2п .
, функция периодты, оның ең кіші оң периоды 2п .
4) функция тақ, өйткені
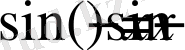 .
.
5)
 кесінділерінде функция бірсарынды өспелі,
кесінділерінде функция бірсарынды өспелі,
 кесінділерінде бірсарынды кемімелі.
кесінділерінде бірсарынды кемімелі.
 нүктелерінің координаталық жазықтыққа түсіріп
нүктелерінің координаталық жазықтыққа түсіріп
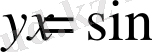 функциясының
функциясының
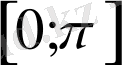 кесіндісінің графигін саламыз.
кесіндісінің графигін саламыз.
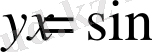 функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
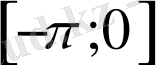 аралығында графикті жалғастырамыз. Сонда,
аралығында графикті жалғастырамыз. Сонда,
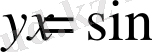 функциясының
функциясының
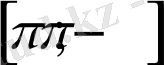 кесіндісіндегі графигін аламыз
кесіндісіндегі графигін аламыз
Сурет-1 Сурет-2
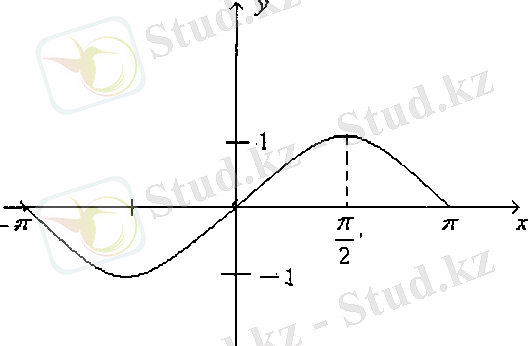
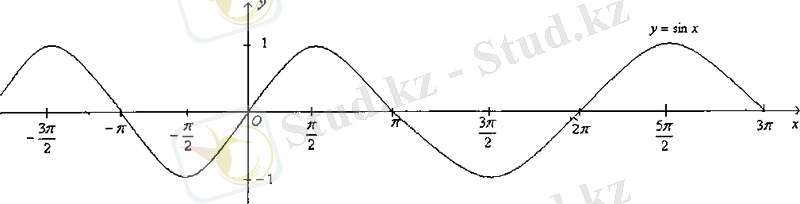 Демек,
Демек,
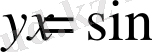 функциясының толық бір период ішіндегі графигін салдық. Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функция графигін салуға болады.
функциясының толық бір период ішіндегі графигін салдық. Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функция графигін салуға болады.
Сурет-3
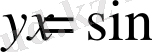 функциясының графигін синусоида қисығы деп атайды.
функциясының графигін синусоида қисығы деп атайды.
2
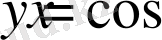 Функциясын қарастырамыз.
Функциясын қарастырамыз.
Функцияның:
1) анықталу облысы -барлықнақты сандар жиыны, яғни .
2) мәндер жиыны
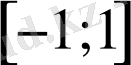 кесіндісі, яғни
кесіндісі, яғни

3)
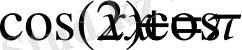 , функция периодты, ең кіші оң периоды 2π .
, функция периодты, ең кіші оң периоды 2π .
4) функция жұп, өйткені
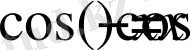
5)
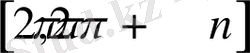 ,
,
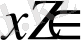 кесінділерінде бірсарынды кемімелі және
кесінділерінде бірсарынды кемімелі және
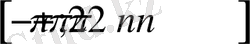
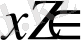 кесінділерінде бірсарынды өспелі функция.
кесінділерінде бірсарынды өспелі функция.
 нүктелерін координаталық жазықтықта белгілеп,
функциясының
нүктелерін координаталық жазықтықта белгілеп,
функциясының
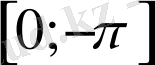 кесіндідегі графигін саламыз (7-сурет) .
кесіндідегі графигін саламыз (7-сурет) .
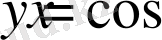 функциясы жүп функция болгандықтан, оның графигі ордината осіне қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
функциясы жүп функция болгандықтан, оның графигі ордината осіне қарағанда симметриялы қисық. Осы қасиетті пайдаланып,
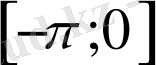 аралығында графикті жалғастырамыз. Сонда,
аралығында графикті жалғастырамыз. Сонда,
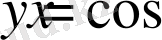 функциясының
функциясының
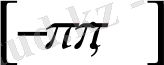 кесіндісіндегі графигін аламыз.
кесіндісіндегі графигін аламыз.
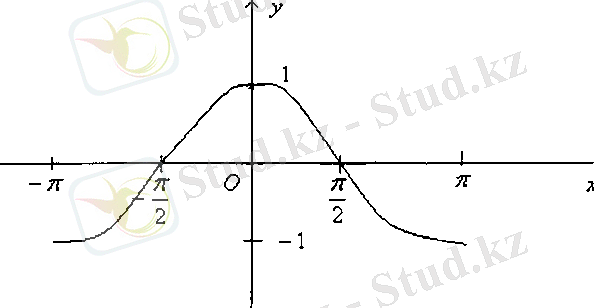
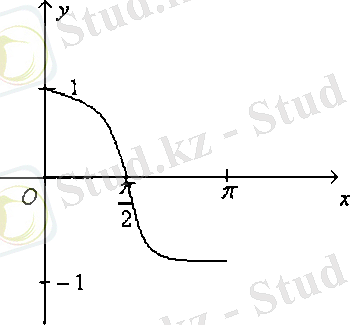
Сурет-4 Сурет-5
Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функцияның графигін салуға болады (8-сурет) .
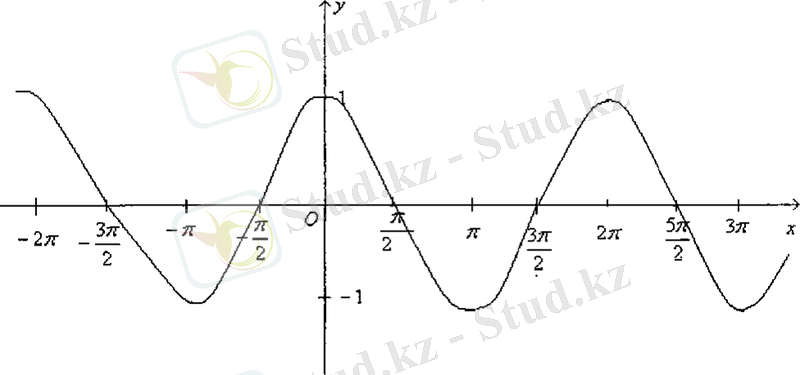
Сурет-6
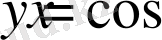 функциясының графигін косинусоида қисығы деп атайды.
функциясының графигін косинусоида қисығы деп атайды.
Сонымен қатар
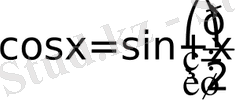 екенін ескеріп
екенін ескеріп
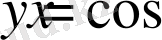 функциясының графигін
функциясының графигін
 функциясының графигінен Ох осінің бойымен
функциясының графигінен Ох осінің бойымен
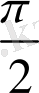 қашықтығына теріс бағытта параллель көшіру арқылы да алуға болады.
қашықтығына теріс бағытта параллель көшіру арқылы да алуға болады.
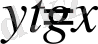 Функциясын қарастырайық.
Функциясын қарастырайық.
Функцияның:
- Анықталу облысыжиынынан басқа барлық нақты сандар
- Мәндер жиыны - барлық нақты сандар жиыны, яғни
- функция периодты π саны;
- функция тақ, өйткені
- , интервалдарында функция бірсарынды өспелі.
Енді функциясының графигін салайық.
 нүктелерін координаталық жазықтыққа белгілеп,
нүктелерін координаталық жазықтыққа белгілеп,
 аралығында
аралығында
 функциясының графигін саламыз.
функциясының графигін саламыз.
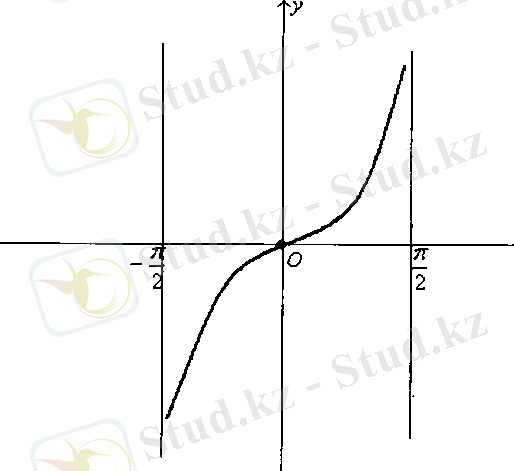
Сурет-7 Сурет-8
Функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық екенін ескеріп,
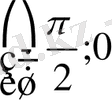 жалғастырамыз. Сонда
функциясының
жалғастырамыз. Сонда
функциясының
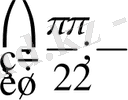 интервалында графигі шығады.
интервалында графигі шығады.
Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы функцияның графигін салуға болады.
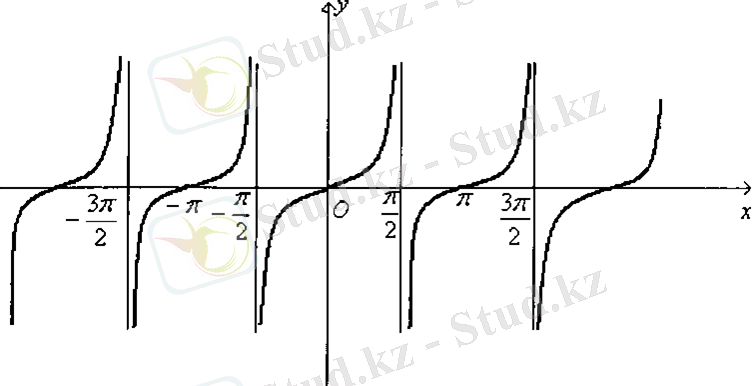
Сурет-9
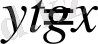 функциясының графигін тангенсоида қисығы деп атайды.
функциясының графигін тангенсоида қисығы деп атайды.
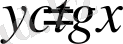
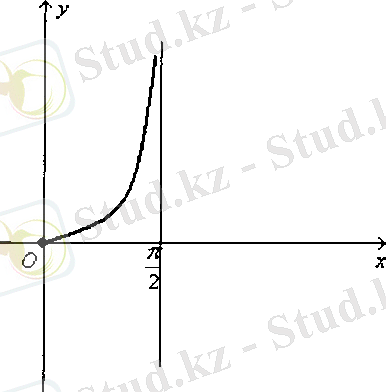
Функциясын қарастырайық
Функцияның:
- анықталу облысы:жиынынан басқа барлық нақты сандар жиыны себебі,
- мәндер жиыны - барлық нақты сандар жиыны, яғни
- тақ функция. Негізгі периоды π.
- функция тақ, өйткені
- интервалында бірсарынды өспелі. функциясы тақ функция болғандықтан, оның графигі у нүктеге қарағанда симметриялы қисық.
Енді периодты функцияның қасиетін пайдаланып, барлық анықталу облысындағы Функцияның графигін салуға болады (13-сурет) .
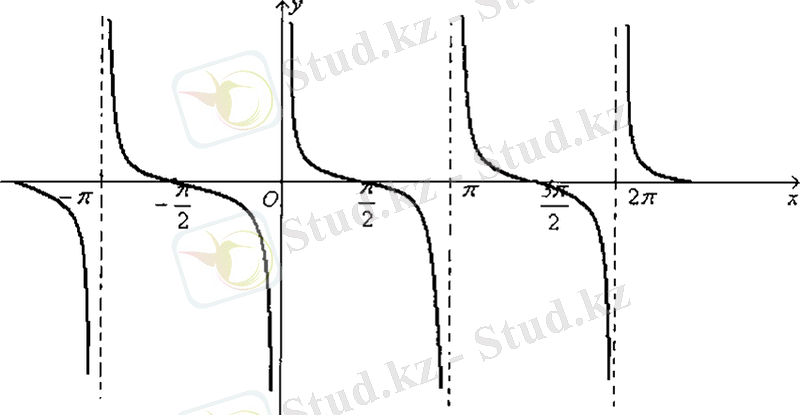
Сурет-10
функциясының графигін котангенсоида қисығы деп атайды
1. 2 Математика курсындағы теңсіздіктер мен теңсіздіктер жүйесінің түрлері
Белгісізі (айнымалысы) тригонометриялық функцияның аргументі түрінде берілген теңсіздікті тригонометриялық теңсіздік деп атайды.
Тригонометриялық теңсіздіктер жүйесін шешу жолдарын үйрету үшін қарапайым тригонометриялық теңсіздіктің шешу жолдарын білу керек. Тригонометриялық теңсіздіктердің жүйесін шешуді қарапайым тригонометриялық теңсіздіктерді шешуден бастаймыз. Себебі кез келген тригонометриялық теңсіздіктер тепе-тең түрлендірілгеннен кейін мына теңсіздіктердің ең болмаганда біреуіне келеді:

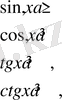
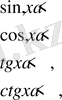
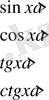 (1)
(1)
мұндағы
Тригонометриялық теңсіздіктерінің жүйелерін шешудің ең тиімді жолы ол бірлік шеңберді пайдалану арқылы шығару әдісі.
Мысалы:
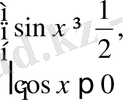 түріндегі теңсіздіктер жүйесі берілсін
түріндегі теңсіздіктер жүйесі берілсін
Енді жүйені шешу алгоритмі:
1) Бірінші теңсіздікті шешеміз:
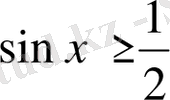
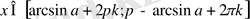 -Дөңгелек жақшалар төртбұрышпен ауыстырылады, себебі нүктенің өзі интервалға қосылады.
-Дөңгелек жақшалар төртбұрышпен ауыстырылады, себебі нүктенің өзі интервалға қосылады.
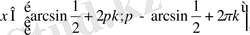
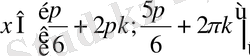
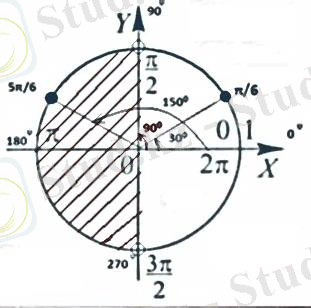
2) Енді осы интервалды бірлік шеңберінде көрсету керек, мұны қалай істеуге болады?
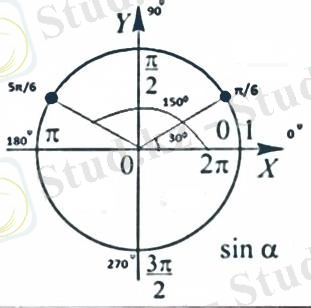
Сурет 1
Ширектерді көрсете отырып, сондай-ақ
 және
және
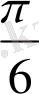 нүктелерін белгіліп аламыз, бұл шын мәнінде 30 және 150 градус. Осыдан 30 градустан 150 градусқа дейінгі шеңбердің доғаны бірінші теңсіздіктің шешуі болып табылады.
нүктелерін белгіліп аламыз, бұл шын мәнінде 30 және 150 градус. Осыдан 30 градустан 150 градусқа дейінгі шеңбердің доғаны бірінші теңсіздіктің шешуі болып табылады.
3) Екінші теңсіздікті шешіміз.
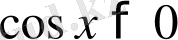
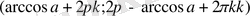
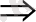
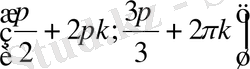
4) Алынған шешімді шеңберде кескіндейміз
Сурет 2
5) Екі аймақтың біріккен аумағын штрихтаймыз.
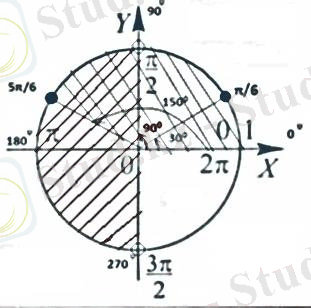
6) Шешім болып табылатын аймақты көрсетеміз.
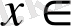
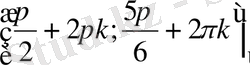
 бір айналымды береді, онда
бір айналымды береді, онда
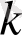 - оң сан.
- оң сан.
тригонометриялық теңсіздігі
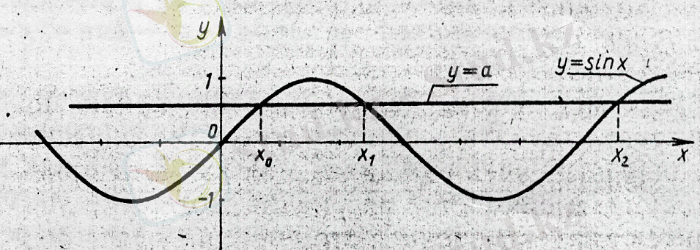
Тригонометрияық теңсіздікті графиктік тісілмен шешудің мысалы ретінде теңсіздігін қарастырайық. Алдымен у= функциясының графигі мен у= түзуінде бір координаталық жазықтыққа саламыз.
у= функциясының периоды 2π-ге тең болғандықтан, берілген теңсіздіктің кесіндісіне тиісті барлық шешімдерін табамыз, одан кейін у= функциясының перодттылығын ескереміз.
теңсіздігінің шешімі кесіндісіндегі у= функциясының графигі у= түзуінің графигінен жоғары орналасқан немесе графикті қиятын х айнымалысының барлық мәндері, яғни кесіндісі. у= функциясының периоды 2π-ге тең болғандықтан, табылған шешімдерге сандарын қоссақ, берілген теңсіздіктің қалған шешімдері табылады. Демек, теңсіздігінің шешімі , .
Тригонометриялық теңсіздіктерді бірлік шеңбердің көмегімен шығаруға болады.
теңсіздігін бірлік шеңбердің көмегімен шығарайық.
Алдымен координаталық жазықтықта бірлік шеңбер саламыз және у= түзуін жүргіземіз (21. 1, ә-суреті) . -тің мәні -ден үлкен немесе тең болғандықтан шеңбердің у= түзуінен жоғары жатқан бөлігін аламыз. Енді бірлік шеңбердің у= түзуімен қиылысу нүктелеріне сәйкес бұрыштарды анықтаймыз. және .
Демек, , у= функциясының периодын ескеріп , ., аламыз.
тригонометриялық теңсіздігі
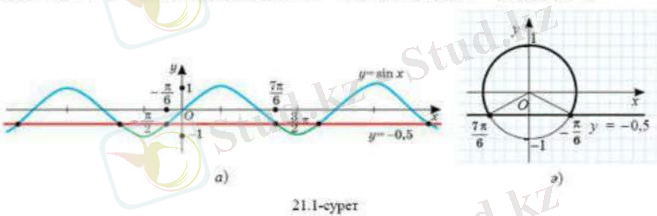
Тригонометрияық теңсіздікті графиктік тісілмен шешуді теңсіздігін шешу мысалы арқылы қарастырайық. Алдымен у= функциясының графигі мен у= түзуінде бір координаталық жазықтыққа саламыз.
у= функциясының периоды 2π-ге тең болғандықтан, берілген теңсіздіктің кесіндісіне тиісті барлық шешімдерін табамыз, одан кейін у= функциясының перодттылығын ескереміз.
теңсіздігінің шешімі кесіндісіндегі у= функциясының графигі у= түзуінің графигінен төменгі жағында орналасқан немесе графикті қиятын х айнымалысының барлық мәндері, яғни кесіндісі. у= функциясының периоды 2π-ге тең болғандықтан, табылған шешімдерге сандарын қоссақ, берілген теңсіздіктің қалған шешімдері табылады.
Демек, теңсіздігінің шешімі , .
теңсіздігін бірлік шеңбердің көмегімен шығарайық.
Алдымен координаталық жазықтықта бірлік шеңбер саламыз және у= түзуін жүргіземіз. -тің мәні -ден кем болғандықтан шеңбердің у= түзуінен жоғары жатқан бөлігін аламыз. Енді бірлік шеңбердің у= түзуінен сол жақта орналасқан бөлігін аламыз. Енді шеңбер мен түзудің қиылысу нүктелеріне сәйкес бұрыштарды анытаймыз.
және . Сонда . Демек, у= функциясының периодын ескеріп, + , . аламыз.
тригонометриялық теңсіздігі
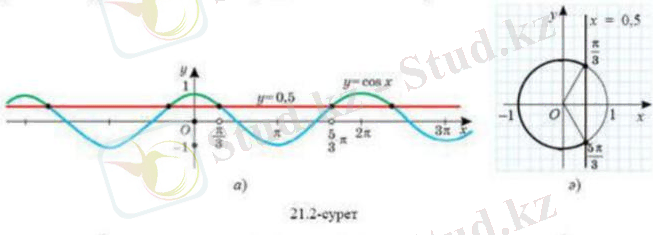
Тригонометрияық теңсіздікті графиктік тісілмен шешудің мысалы ретінде теңсіздігін қарастырайық. Алдымен у= функциясының графигі мен у= түзуін бір координаталық жазықтыққа саламыз.
у= функциясының периоды π-ге тең болғандықтан, берілген теңсіздіктің кесіндісіне тиісті барлық шешімдерін табамыз, одан кейін у= функциясының перодттылығын ескереміз.
теңсіздігінің шешімі кесіндісіндегі у= функциясының графигі у= түзуінің графигінен төмен орналасқан немесе графикті қиятын х айнымалысының барлық мәндері, яғни жарты интервалы.
у= функциясының периоды π-ге тең болғандықтан, табылған шешімдерге сандарын қоссақ, берілген теңсіздіктің қалған шешімдері табылады.
Демек, теңсіздігінің шешімі , , жиыны болады.
тригонометриялық теңсіздігі
Тригонометрияық теңсіздікті графиктік тісілмен шешудің мысалы ретінде теңсіздігін қарастырайық. Алдымен у= функциясының графигі мен у= түзуін бір координаталық жазықтыққа саламыз.
у= функциясының периоды π-ге тең болғандықтан, берілген теңсіздіктің кесіндісіне тиісті барлық шешімдерін табамыз, одан кейін у= функциясының перодттылығын ескереміз. (21. 4 -сурет)
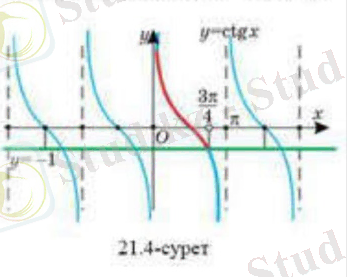
теңсіздігінің шешімі кесіндісіндегі у= функциясының графигі у= түзуінің графигінен жоағары орналасқан немесе графикті қиятын х айнымалысының барлық мәндері, яғни жарты интервалы.
у= функциясының периоды π-ге тең болғандықтан, табылған шешімдерге сандарын қоссақ, берілген теңсіздіктің қалған шешімдері табылады.
Демек, теңсіздігінің шешімі , , жиыны болады
2. МАТЕМАТИКА КУРСЫНДАҒЫ ТРИГОНОМЕТРИЯЛЫҚ ТЕҢСІЗДІКТЕР МЕН ТЕҢСІЗДІКТЕР ЖҮЙЕСІН ШЕШУДІ ОҚЫТУ ӘДІСТЕМЕСІ
2. 1 Қарапайым тригонометриялық теңсіздіктер мен теңсіздіктер жүйесін шешу әдістері
Тригонометриялық теңсіздіктерді шешу үшін бірнеше маңызды кезеңдерден өту керек. sin x, cos x, tg x и ctg x ұғымдарын енгізу . Радиусы 1-ге тең, центрі координаталар басында жататын шеңберді бірлік шеңбер деп атайды. Бірлік шеңбердің Р а нүктесі Р 0 (1; 0) нүктесін а радианға тең бұрышқа бұрғанда шыққан болсын. Р а нүктесінің координатасы - а бұрышының косинусы екенін аңғару қиын емес
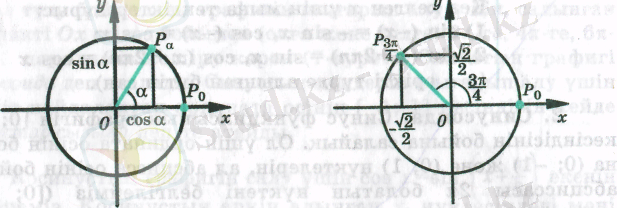
Анықтама. у = sin х және у = cos х формулаларымен берілген сандық функцияларды сәйкесінше синус және косинус деп атайды
Анықтама. у = tg х және у = ctg х формулаларымен берілген сандық функцияларды сәйкесінше тангенс және котангенс деп атайды
- Келесі қадам функцияларды енгіземіз y = sin x, y = cos x, y = tg x и y = ctg x. Бұл кезеңде осы функциялардың қасиетері, анықталу облысы мен мәндер облысы қарастырылып өтеді, ал ең маңызды - графиктерімен танысу.
- Тригонометриялық теңсіздіктерді шешуге дайындыққа ең соңғы кезең. Бұл кезеңде оқушылар маңызды тригонометрия формулаларымен және оларды қалай қолдану керек екендігімен танысады. Бұл кезеңде алынған білімін оқушылар бүкіл математика курсында колдана алады. Меңгерілген формулалар көмегімен өте қиын, көлемді тригонометриялық теңдеулер мен теңсіздіктерді жеңіл шешуге болады.
Енді оқушылар бастапқы кезеңдерді жақсы меңгеріп, біздің тақырыбымызға жетеді, яғни тригонометриялық теңсіздіктерге жетеді. Әрине теңсіздіктерді шешу қарапайымдардан басталады sin x > a, sin x < a; cos x > a, cos x < a; tg x > a, tg x < a. Осы теңсіздіктерді меңгергеннен кейін қиындығы жоғары теңсіздіктерге келеді, бұнда әр түрлі дәрежелі күрделі функциялар. Әрине 16-17 жастағы балалар үшін мұндай материалды меңгеруді жеңіл деп айта алмайсың. Ол абстракті ойлауды, мидың аналитикалық қалыптасуы және ең маңыздысы ойлаудың шапшаңдығын қажет етеді. Сол себептен бұндай күрделі материалды Егер қарапайым теңсіздіктер өзі шешіліп тұрса, онда теңсіздіктерді шешуге арнайы әдіс-тәсілдердің ойластырылуының қажеті не? Бірақ бұған жауап беруге болады, кез - келген тригонометриялық теңсіздік, сырттан қарағанда ауқымды және күрделі болып көрінсе де оларға негізгі тригонометриялық түрлендірулерді қолданып қарапайым түрге келтіруге болады. Түрлендіргеннен кейін теңсіздікті тригонометриялық шеңбер арқылы немесе функцияның графигі арқылы шешеміз.
Негізінде мектеп курсында тригонометриялық теңдеулерді шешуде қандай әдісті қолдану тиімді екендігі жөнінде нақты нұсқаулар жоқ. Бұл жерде таңдау тек мұғалімдердің өз қалауларына байланысты болады. Менің ойымша тригонометриялық шеңберді қолдану тиімдірек болады. Себебі бұл өте көрнекі тәсіл және дәптерде аз орын алады. Негізі қарапайым тригонометриялық теңсіздіктерді шығарған кезде уақыт мүмкіндік беріп жатса екі тәсілді де қолданған жөн. Сонымен айтып кеткенімдей тригонометриялық теңсіздіктеріне тригонометриялық түрлендірулер қолданып оны қарапайым түрге келтіргеннен кейін тригонометриялық шеңбер немесе графикалық әдісті қолданамыз.
Қарапайым тригонометриялық теңсіздіктерді шешу: Заманауи математика кітаптарының көптеген авторлары көрсетілген тақырыпты қарастыруды жеңіл тригонометриялық теңсіздіктерді шешуден бастауды ұсынады. Қарапайым тригонометриялық теңсіздіктерді шешу қағидасы тригонометриялық дөңгелекте тек қана негізгі тригонометриялық бұрыштарды анықтап және білуге ғана емес, сонымен қатар басқа да белгілерге негізделген. Сонымен қоса, мына теңсіздіктерді шешуді
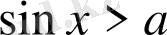 ,
,
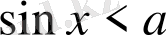 ,
,
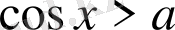 ,
,
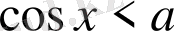 келесі түрде жүзеге асыруға болады: алдымен көрсетілген теңсіздік орындалатын бір кеңістікті тауып аламыз (
келесі түрде жүзеге асыруға болады: алдымен көрсетілген теңсіздік орындалатын бір кеңістікті тауып аламыз (
 ), содан соң синус пен косинустың ара қашықтығында табылған кеңістікті тауып жазамыз: (
), содан соң синус пен косинустың ара қашықтығында табылған кеңістікті тауып жазамыз: (
 ) . Сонымен қатар,
) . Сонымен қатар,
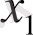 мағынасы жеңіл табылады ол
мағынасы жеңіл табылады ол
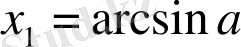 және
және
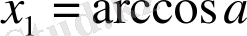 .
.
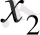 мағынасын табу оқушылардың ойлау қабілеттеріне, олардың синус пен косинустың бөлек симетрияларын қолдану арқылы доғаның немесе бөлшектердің теңдіктерін табуларына байланысты болып келеді. Бұл көп жағдайда көптеген оқушылардың шеше алмаулары алып келеді. Соңғы жылдары кітаптардағы көрсетілген қиындықтарды шешу мақсатында жеңіл тригонометриялық теңсіздіктерді шешу үшін әртүрлі шаралар жүзеге асырылған бірақ оқыту барысында ешқандай оң нәтижелер берген жоқ. Біз ұзақ жылдар бойы тригонометриялық теңсіздіктерді шешу үшін сәйкес келетін теңдеулердің түбір формулаларын қолданып келеміз.
мағынасын табу оқушылардың ойлау қабілеттеріне, олардың синус пен косинустың бөлек симетрияларын қолдану арқылы доғаның немесе бөлшектердің теңдіктерін табуларына байланысты болып келеді. Бұл көп жағдайда көптеген оқушылардың шеше алмаулары алып келеді. Соңғы жылдары кітаптардағы көрсетілген қиындықтарды шешу мақсатында жеңіл тригонометриялық теңсіздіктерді шешу үшін әртүрлі шаралар жүзеге асырылған бірақ оқыту барысында ешқандай оң нәтижелер берген жоқ. Біз ұзақ жылдар бойы тригонометриялық теңсіздіктерді шешу үшін сәйкес келетін теңдеулердің түбір формулаларын қолданып келеміз.
Көрсетілген тақырыпты зерттеу келесі түрде жүзеге асырылады:
- және у = а кестесін құрамыз, санаймыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz