Қысқа жолды іздеу алгоритмдері

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 39 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министрлігі Л.Н. Гумилев атындағы Еуразия ұлттық университеті

Айса Бейбарыс Бауыржанұлы

Тақырыбы: Дейкстра алгоритмы және оны тасымалдау төлемақысын санау кезінде тарифтік арақашықтықты табуға пайдалану

ДИПЛОМДЫҚ ЖҰМЫС

5В070500 - Математикалық және компьютерлік моделдеу мамандығы

Қазақстан Республикасының Білім және ғылым министрлігі Л.Н. Гумилев атындағы Еуразия ұлттық университеті

Қорғауға жіберілді
Математикалық және компьютерлік моделдеу кафедрасының меңгерушісі
Адамов А.А
2022 ж.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Дейкстра алгоритмы және оны тасымалдау төлемақысын санау кезінде тарифтік арақашықтықты табуға пайдалану

5В070500 Математикалық және компьютерлік моделдеу мамандығы бойынша

Орындаған Б.Б.Айса

Ғылыми жетекшісі
ф.-м.ғ.к., қауым. профессор М.Б.Габбасов

Л.Н. Гумилев атындағы Еуразия ұлттық университеті Механика - математика факультеті
Математикалық және компьютерлік моделдеу кафедрасы 5В070500 - Математикалық және компьютерлік моделдеу мамандығы

БЕКІТЕМІН
Кафедра меңгерушісі
А. А. Адамов
20 ж.

Студент Айса Бейбарыс Бауыржанұлы_
(тегі, аты, әкесінің аты)

4-курс, МКМ-41 тобы, 5В070500 − Математикалық және_
компьютерлік моделдеу мамандығы, күндізгі_ (курс, тобы, мамандық, оқу формасы)

Диплом жұмысты орындауға арналған ТАПСЫРМА

1. Жұмыстың тақырыбы Дейкстра алгоритмы және оны тасымалдау төлемақысын санау кезінде тарифтік арақашықтықты табуға пайдалану
университет бойынша 2022ж. 14 қаңтар берілген №47-n бұйрығымен бекітілген.

2. Студент аяқтаған жұмысты тапсыру мерзімі 28 мамыр 2022 ж.

3. Жұмыстың бастапқы деректері: дипломдық жұмыс тақырыбы бойынша ғылыми мақалалар, сондай-ақ заманауи басылымдар, зерттеліп, ғылыми әдебиет көздері пайдаланылды

4. Дипломдық жұмысты дайындауға қатысты сұрақтар тізімі: Екі стансаның арасындағы тарифтік арақашықтықты Дейкстра әдісімен табатын программа жазу

5. Графикалық материалдың тізбесі: 28 сурет

6. Негізгі ұсынылған әдебиеттер тізімі

1. Березина Л. Графы и их применение. М.: Просвещение, 1979 г. 2. Зыков А. А. Основы теорий графов. М.: Наука, 1987г.
3. Евстигнеев В. А. Применение теорий графов в программиро-
вании под редакцией Ершова А. П. - М: Наука, 1985 г.
4. Татт У. перевод с английского Гаврилова Г. П. - М: Мир,
1988г.
5. Оре О. перевод с английского Врублевская И. Н. - М: Наука,
1980г.
6. Емеличев В. А. Лекции по теории графов В. А. Емеличев и др.
- М.: Наука, 1990.
7. Кристофидес Н. Теория графов. Алгоритмический подход
Н. Кристофидес. - М.: Мир, 1978.
8. Ловас Л . Прикладные задачи теории графов Л. Ловас,
М. Пламмер. - М.: Мир, 1998.
9. Новиков Ф. А. Дискретная математика для программистов Ф.
А. Новиков. - СПб.: Питер, 2001.

7. Жұмыс бойынша тиісті бөлімдерде көрсетілген кеңестер

Бөлім атауы және нөмірі

Ғылыми жетекші, Кеңесші

Тапсырма алу мерзімі

Тапсырманы бердім (қолы)

Тапсырманы алдым (қолы)
1.Графтар теориясының негіздері
М.Б.Габбасов

1.2.Темір жол стансаларынан тұратын граф салу
М.Б.Габбасов

2. Дейкстра алгоритмін игеру
М.Б.Габбасов

2.1.Қысқа жолды іздеу алгоритмдері
М.Б.Габбасов

2.2.Қысқа жолды іздеу процесі
М.Б.Габбасов

3.Екі стансаның арасындағы тарифтік арақашықтықты Дейкстра әдісімен табатын программа жазу
М.Б.Габбасов

8. Дипломдық жұмысты орындау кестесі

№

Жұмыс кезеңі
Жұмыс кезеңін орындау
мерзімі

Ескертпе
1
Дипломдық жұмыстың тақырыбын
бекіту

2
Дипломдық жұмысты дайындау
үшін материалдар жинау

3
Дипломдық жұмыстың теориялық
бөлімін дайындау (1 Бөлім)

Тәжірибеге
кеткенге дейін
4
Дипломдық жұмыстың сараптау бөлімін дайындау ( 3 Бөлімдер)

Тәжірибе барысында

5
Дипломдық жұмыстың толық мәтінінің қолжазбалық нұсқасын аяқтау

Тәжірибе аяқталғаннан кейінгі бірінші
аптада
6
Дипломдық жұмысты алдын ала қорғауға ұсыну

Шолу дәрістері
барысында (кеңес беру)
7
Дипломдық жұмысты пікірлемеге
ұсыну

8
Ғылыми жетекшінің пікірі мен пікірлеме бар дипломдық жұмыстың
тодық нұсқасын ұсыну

9
Дипломдық жұмысты қорғау

МАК кестесіне сай

Тапсырманы беру күні 14 қаңтар 2022ж.

Ғылыми жетекші, ф.-м.ғ.к., қауым. профессор М.Б.Габбасов Тапсырманы қабылдады: студент __Б.Б.Айса

МАЗМҰНЫ
КІРІСПЕ 9
1. Теориялық бөлім 11
1.1 Графтар теориясының негіздері 11
1.2 Темір жол стансаларынан тұратын граф салу 22
2. Дейкстра алгормін игеру 30
2.1 Қысқа жолды іздеу алгоритмдері 31
2.2. Қысқа жолды іздеу процесі 32
3. Практикалық бөлім 37
3.1 Екі стансаның арасындағы тарифтік арақашықтықты Дейкстра әдісімен табатын программа жазу 37
ҚОРЫТЫНДЫ 43
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 44
ҚОСЫМША 46

КІРІСПЕ

Жергілікті тарифтерді тeмip жолдың басшылары белгілейді. Жүктерді тасымалдағаны үшін төленетін ақы және түрлі жинақ, қойылымдары кіретін бұл тарифтер берілген темір жол шеңберінде қызмет етеді.
Темір жол бойымен жүк үлкен, жолаушылар немесе жүктік жылдамдықпен тасымалдануы мүмкін. Жылдамдық түpi жүктің тәулігіне қанша килoметр жүруі тиіс екенін анықтайды.
Тарифтік қашықтық осы тасымалдау ара қашықтығы болып табылады. Тасымалдау ақысы ең қысқа бағыттағы ара қашықтық бойынша алынуы мүмкін, жүктік немесе үлкен жылдамдықпен жүктерді тасымалдау кезінде тарифтік қашықтыққа немесе габариттік емес жүктерді немесе жүктерді жолаушылар жылдамдығымен тасымалдау кезінде нақты өткен кашықтық үшін алынуы мүмкін.
Жүктердің тасымалдауы жүргізілетін вагон типі түрліше келеді.Темір жол бойымен жүктер әртүрлі, арнайы немесе изотермиялық вагондарда, цистерналарда немесе платформаларда тасымалдануы мүмкін. Тасымалдау ақысы әр жағдайда әр түрліше болады.Тасымалданатын жүктердің саны -- тасымалдауға маңызды әсер ететін фактор.
Дипломдық жұмыстың мақсатына орай бұл тарифтік қашықтықты есептеуге графтар көмекке келеді.Яғни,Дейкстра алгоритмін тақырыпқа сәйкес темір жол логистикасында қолданылу аясында графтар негізгі рөл атқарады.
Графтар теориясы - графтардың қасиетін оқытатын дискретті математиканың бір бөліміне жатады. Графтар теориясының практикалық мүмкіндіктері өте зор. Түрлі білім салаларында, мысалы психология, химия, электротехника, сонымен қатар көлік тасымалдауда, басқаруда, сауда-саттықта жəне білім беруді жоспарлауда туындайтын кейбір проблемалар графтар теориясының мəселесі ретінде қалыптасуы мүмкін. Осы жағдайларға байланысты графтар теориясы өз алдына қызықты деп қана саналмай, алынған нəтижелерін жинақтайтын, біліктендіретін, жалпылайтын жəне жан-жақты тарататын білімнің түрлі аймағындағы басты негіздерін көрсетеді.Мысалы, графтар теориясы геоақпараттық жүйелерде де қолданылады. Жаңадан жоспарланған немесе салынған үйді қайта жоспарлауда, құрылыстарда, нысандарда жəне т.б. ол төбелері ретінде қарастырылса, олардың жолдарының бірігуін, инженерлік желілер, электротасымалдау желілері жəне т.б. - оның қабырғасы ретінде қарастырылады. Сонымен қоса, ең қысқа айналу жолын немесе ең жақын азық-түлік дүкенін табу сияқты графтардан шығатын түрлі есептеулерді қолдану тиімді бағдарларды жоспарлауға мүмкіндік береді.
Бүгінгі таңда көптеген адамдар маршрутты құру үшін навигаторларды, электронды карталарды пайдаланады. Бұл уақытты қысқартуға, жолды алдын-ала жоспарлауға мүмкіндік береді. Қала масштабындағы навигациядан бастап ғимарат ішіндегі навигацияға дейін бәрі мобильді немесе веб - қосымшалар арқылы жүреді.
Web-қосымшаның қарапайым сайттан айырмашылығы пайдаланушының ресурстағы деректермен өзара әрекеттесуі болып табылады. Ол әр түрлі нысандарды толтыра алады, жеке кабинет арқылы тапсырмаларды орындай алады және т. б.
Бұл жұмыстың мақсаты Дейкстер әдісімен екі станция арасындағы тарифтік қашықтықты табу бойынша сервисті әзірлеу және іске қосу болып табылады. Осы міндетке сәйкес іске асырудың оңтайлы әдістерін таңдау қажет, олардың өлшемдері пайдалану ыңғайлылығы, деректерді өңдеу жылдамдығы, нәтижелердің көрінуі мен дәлдігі болып табылады. Ол үшін таңдау керек:
1) бағдарламалау тілі
2) web-сервер
3) ең қысқа жолды табу алгоритмі
4) қосымшаны әзірлеу құралдары

Бұл дипломдық жұмыстың негізгі мақсаты графтың бойындағы ең қысқа арақащықтықты табуға арналған Дейкстра алгоритмін игеріп және оны тасымалдау төлемақысын санау кезінде екі стансаның арасындағы тарифтік арақашықтықты табатын программада пайдалану көзделген.
Бірінші бөлімде дипломдық жобаның тақырыбы бойынша зерттеу жүргізуге қажетті барлық графтар туралы толық мәліметтер, тақырыпқа сәйкес қолданылуын келтіреміз.
Екінші бөлімде Дейкстра алгоритмінің маңызын ашамыз.Сондай-ақ есепте қолданылуын жіті назарға алып,алгоритм бойынша күрделі жұмыс жүргіземіз.
Үшінші бөлімде тәжірибе жүзінде нақты көрсете отырып негізгі бөлімнің маңызын осы python тілінде бағдарламалап түсіреміз.
Қорытындылай келе, дипломдық жобаның тақырыбы бойынша алынған зерттеу нәтижелері мен қолданылу аясы қорытындыланады.
Пайдаланылған әдебиеттер тізімінде 23 әдебиет бар.

Теориялық бөлім
1.1 Графтар теориясының негіздері

Графтар ғылым мен практиканың түрлі салаларындағы математикалық модельдердің маңызды элементтері болып саналады. Графтың көмегімен автоматика, электроника, физика, химия жəне т.б. сияқты білім аймақтарында жинақталған мəселелерді шешуді жеңілдетуге болады. Графтың көмегімен жол, газ құбырлары, жылу жəне электр желілерінің сұлбалары бейнеленеді. Сонымен қатар графтар математикалық жəне экономикалық есептерді шешуде үлкен көмек көрсетеді.
1.1. Граф жəне оның түрлері
Бөлімімізді графтар теориясының негізгі ұғымдарынан бастайық. Осы ұғымдарға негізделген бірнеше нəтижелерді келтірейік.
Граф анықтамасын қарапайым сөзбен түсіндірсек ол нүктелер жиынынан (графтың төбелері) тұратын жəне осы нүктелер жиынын қосатын түзу немесе қисық кесінділерден (граф қабырғалары) тұратын сұлбаны айтамыз. Граф G=(V, E) екі жиыннан, яғни шекті жиындар элементтерінен тұрады. Бұл жерде G - граф, ал V - графтың төбелері, E - графтың қабырғалары деп аламыз.

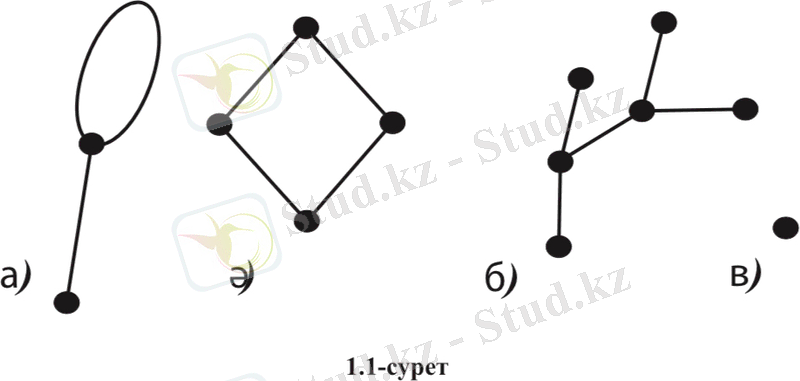
Графтар, негізінен, геометриялық фигура түрінде бейнеленеді, сондықтан графтың төбелері нүкте арқылы, қабырғалары нүкте- лерді бір-бірімен қосатын сызықтар арқылы бейнеленеді (1.1-сурет).
Графтың шеткі төбелері бірдей болса, онда барлық қабырға- лары параллель болып табылады. Ал, егер қабырғасының басы мен соңы бір төбеде орналасса (1.1 а-суретте), онда оны ілмек деп атаймыз. Жалпы айтқанда, ілмектің бағыты болмайды. Бірақ бағытталған графтарды аралас графтардан ажырату үшін бағытталған графтарда ілмектің бағыты көрсетіледі.
Ілмек - бұл бастапқы жəне шеткі доғаның бір-бірмен сəйкес- тенуі.
Ілмексіз жəне параллель қабырғасыз графтар қарапайым граф деп аталады. Графтың төбелерінің жиыны n элементтен тұратын болса, онда G граф n-ретті граф болады.
Қабырғалары жоқ графтар бос граф деп аталады (1.1 в-сурет). Ал, егер графтың төбелері жоқ болса (онда əрине қабырғалары да жоқ), онда мұндай граф нөл-граф деп аталады.
Графикалық графтар диаграмма түрінде де берілуі мүмкін, онда төбелері нүктемен немесе дөңгелекпен, ал қабырғалары сəйкес қабырға төбелерінің шеттеріндегі нүктелер немесе дөң- гелектерді қосатын сызық кесінділермен бейнеленеді (1.1 а, ə-сурет).
Графтарды суретте немесе сұлбада бейнелегенде кесінділері түзу сызық немесе қисық сызық түрінде, ал кесінділердің ұзындықтары мен нүктелердің арақашықтықтары əртүрлі түрде берілуі мүмкін. Əрбір қабырға жұптасқан төбелер арқылы анықталады. Егер графтың қабырғалары реттеліп жұптасқан төбелер арқылы анықталса, онда G бағытталған граф (сызықтары доға түрінде болады) деп аталады. Кері жағдайда, оны G бағытталмаған граф (сызықтарының бəрі қабырғасы болып табылады) деп атаймыз.
Егер графтың əртүрлі екі төбесі бір-бірімен тек қана бір қабырға арқылы қосылған болса, онда ол толық граф деп аталады. Əртүрлі төбелерінің əрбір жұбы көршілес болатын қарапайым графты толық граф деп те атауымызға болады. n төбесі бар
толық граф n(n−1) қабырғадан тұрады жəне K деп белгіленеді 2n
(1.2-сурет). n - 1 дəрежелі граф тұрақты граф болып табылады.

Графтың толық болуы немесе болмауы оның жалпы сипаттама- сына байланысты болады.
Графтың төбелерінің əрбір жұбы бір бағытталған қабырғамен дəл қосылған болса, ондай графтарды толық бағытталған граф деп атаймыз. Егер толық бағытталған графтың əрбір қабырғасында көрсетілген бағыттарын алып тастасақ, онда ол бағытталмаған қабырғалары бар толық графқа айналады.
Графтың төбелері бір-бірінен олардың қанша қабырғаға жататындығына байланысты ажыратылады.
Егер графтың қабырғасының ұштарының орналасу реті еске- рілмейтін болса, онда оны бағытталмаған қабырға деп атайды.
Егер графтың қабырғасының ұштарының орналасу реті ескерілетін болса, онда оны бағытталған қабырға деп атайды. Бұл жағдайда g(xi, xj) қабырғасының басы xi төбесі, ал соңы xj төбесі деп аталады.
Бағытталған қабырға графтың доғасы деп те аталады.
Егер графта бағытталған жəне бағытталмаған да қабырғалар бар болса, онда оны аралас граф деп атайды.
G(X) графындағы əрбір қабырғаның бағытын қарама-қарсыға (керіге) өзгерту арқылы оған кері граф G-1(X) аламыз. Яғни, əрбір бағытталған графқа кері граф бар.
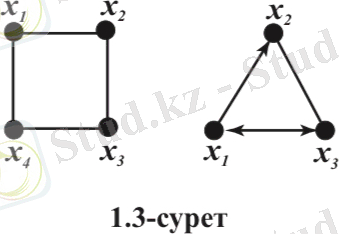
Бағытталмаған толық граф деп кез келген xi, xj О X (i!=j) үшін қабырғалары əртүрлі g(xi, xj) жұптары болатын U(X) графын атайды (1.3-сурет).
Кез келген екі төбесі бірнеше қабырғалармен немесе доғалармен қосылған графты мультиграф деп атайды.

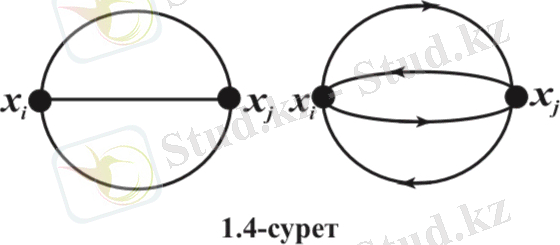
1.4-суретте бағытталмаған жəне бағытталған мультиграфтар берілген.
Қабырғалары G(X) графымен бірге толық U(X) графын беретін Gk(X) графын G(X)-тің толықтаушы граф деп атайды.
Графтағы барлық қабырғалары əр түрлі болатын жолдың бағытын тізбек деп атаймыз. Егер графтың барлық төбелері (сонымен қатар қабырғалары) əр түрлі болса, ондай тізбекті қарапайым тізбек деп атаймыз.
Тұйықталған тізбекті цикл деп атаймыз. Бір төбеден басталып жəне сол төбемен аяқталатын бірден кем емес қарапайым жол ұзындығын бағытталған графтағы цикл дейміз.

Іздеу мәселесінің қазіргі жағдайын талдау қысқа жол.

Графикалық теория-бұл дискретті математиканың саласы, оның ерекшелігі объектілерді зерттеуге геометриялық көзқарас болып табылады. Ол әдетте топологияға жатады (өйткені көптеген жағдайларда графиктердің тек топологиялық қасиеттері қарастырылады), бірақ ол жиын теориясының, комбинаторлық математиканың, алгебраның, геометрияның, матрица теориясының, ойын теориясының, математикалық логиканың және басқа да көптеген математикалық пәндердің көптеген бөлімдерімен қиылысады. Графтар теориясының негізгі объектісі-граф және оны жалпылау.
Графикалық теорияның алғашқы міндеттері математикалық ойын-сауық есептері мен жұмбақтарды шешумен байланысты болды (Кенигсберг көпірлері туралы есеп, шахмат тақтасында патшайымдарды орналастыру туралы есеп, тасымалдау туралы есептер, әлем бойынша саяхат туралы есеп және басқалар). Графтар теориясындағы алғашқы нәтижелердің бірі Л. Эйлердің Кенигсберг көпірлері мәселесін шешуде алған барлық жиектерін қайталамай айналып өту өлшемі болды.
Пазлдар мен ойын-сауық ойындарын шешуде дүниеге келген графикалық теория қазіргі уақытта көптеген мәселелерге қатысты мәселелерді шешудің қарапайым, қол жетімді және қуатты құралына айналды. Бағандар сөзбе-сөз қарапайым. 20 ғ.графиктерге байланысты міндеттер тек физика, химия, электротехника, биология, экономика, әлеуметтану және т. б. ғана емес, сонымен қатар математикада топология, алгебра, ықтималдық теориясы, сандар теориясы сияқты бөлімдерде пайда бола бастады. Ол Қарулы Күштерді айналып өтпеді.
Мемлекеттік шекараны қорғау, оқу-жаттығу шаралары мен әскери операцияларды жүргізу әскерлерді жиі қайта топтастыруды, шерулерді өткізуді талап етеді, ал оларды өткізуге уақыт пен ресурстар шектеулі болғандықтан, бай математикалық аппараты бар графтар теориясы қойылған міндеттерді шешу үшін өте пайдалы болды. Жауынгерлік техниканың немесе бөлімшелердің жаяу тәртіпте дұрыс құрастырылған қозғалыс бағыты тапсырманы тез ғана емес, сонымен қатар сапалы орындауға мүмкіндік береді. Тапсырманы орындау кезінде бұл сізге аз жанармай жұмсауға мүмкіндік береді, ауыр жүктемелерге, күш пен уақытты үнемдеуге байланысты марш кезінде істен шыққан жабдықтардың санын азайтуға көмектеседі, бұл сізге жеке құрамның көңіл-күйін көтеруге мүмкіндік береді. Бұл әсіресе соғыс жағдайында маңызды.
Графтар теориясы бойынша зерттеулер 40-жылдардың аяғы мен 50 - жылдардың басында, ең алдымен кибернетика мен компьютерлік технологияның дамуына байланысты едәуір кеңейді. Компьютерлік технологияның дамуына, күрделі кибернетикалық жүйелерді зерттеуге байланысты графтар теориясына деген қызығушылық артып, графиктер теориясының мәселелері айтарлықтай байытылды. Сонымен қатар, компьютерлерді қолдану бұрын шешілмеген есептеулердің үлкен көлемімен байланысты нақты мәселелерді шешуге мүмкіндік берді. Графикалық теорияның бірқатар экстремалды есептері үшін оларды шешу әдістері жасалды, мысалы, осындай әдістердің бірі желі арқылы максималды ағынды құру мәселелерін шешуге мүмкіндік береді. Бұрын зерттелген және зерттелген графиктердің жеке кластары үшін (ағаштар, жалпақ графиктер және т.б.) осы сыныптардағы графиктер үшін кейбір мәселелерді шешу ерікті графиктерге қарағанда оңай екендігі көрсетілген (берілген қасиеттері бар графиктердің өмір сүру жағдайларын табу, графиктердің изоморфизмін құру және т. б.).
Соңғы үш онжылдықта графикалық теория математиканың қарқынды дамып келе жатқан бөлімдерінің біріне айналды. Бұл тез дамып келе жатқан қосымшалар аймағының сұраныстарына байланысты. Теориялық-графикалық терминдерде дискретті объектілерге байланысты көптеген мәселелер тұжырымдалады. Мұндай міндеттер интегралды схемалар мен басқару схемаларын жобалау кезінде, машиналарды, логикалық тізбектерді, бағдарламалық ағындарды зерттеу кезінде, экономика мен статистикада, химия мен биологияда, кесте теориясы мен дискретті оңтайландыруда туындайды. Осылайша, графикалық теория кибернетиканың математикалық аппаратының маңызды бөліктерінің біріне, Дискретті математика тіліне айналады.
Граф - абстрактілі математикалық объект, ол графиктің шыңдары мен жиектер жиынтығын, яғни шыңдардың жұптары арасындағы қосылыстарды білдіреді. Әр түрлі қосымшалар үшін графиктердің түрлері бағдармен, байланыстар санына шектеулермен және шыңдар мен жиектер туралы қосымша мәліметтермен ерекшеленуі мүмкін. Математика мен информатикаға практикалық қызығушылық тудыратын көптеген құрылымдар графиктермен ұсынылуы мүмкін.
G= (X, U) қарапайым немесе бағдарланбаған графигі реттелген жиындар жұбы деп аталады: элементтері G графигінің шыңдары деп аталатын соңғы бос емес Х және элементтері осы графиктің шеттері деп аталатын 𝑈 ⊆ 𝑋 жиынтығы[3]. X, 𝑦 𝜖 𝑋 шыңдары іргелес, егер 𝑥 𝑦 ∈ 𝑈 болса, ал егер 𝑥 𝑦 ∉ 𝑈 болса, іргелес емес. 𝑥 𝑦 Шеті X және Y шыңдарын , сондай-ақ олардың әрқайсысын кездейсоқ байланыстырады. Бағдарланбаған графиктің мысалы 2-суретте көрсетілген.

Сурет 2.

Жол графикте шыңдардың соңғы тізбегі деп аталады, онда әр шың (соңғысынан басқа) келесі шеттермен ретпен қосылады. Тізбек-бұл қайталанатын жиектері жоқ жол.

Графиктің іргелес матрицасы G шыңдарының соңғы санымен N-Бұл N өлшемінің a квадрат матрицасы, онда 𝑎 𝑖 𝑗 элементінің мәні графиктің I-ші шыңынан j-ші шыңға дейінгі жиектер санына тең[4]. Қарапайым графиктің іргелес матрицасы (ілмектер мен бірнеше жиектер жоқ) екілік матрица болып табылады және негізгі диагональдағы нөлдерден тұрады. 3-суретте көрсетілген график үшін іргелес матрица келесідей болады:

Сурет 3. Іргелес Матрица
Іргелес Матрица және іргелес тізімдер компьютерлік бағдарламаларда графиктерді көрсету үшін қолданылатын негізгі деректер құрылымы болып табылады
Іргелес матрицаны тек жиектері көп, сирек емес графиктер болған жағдайда қолданған жөн, өйткені ол әр элемент үшін бір бит деректерді сақтауды қажет етеді. Егер график сирек болса, онда жадтың көп бөлігі нөлдерді сақтауға жұмсалады, бірақ сирек графиктер болған жағдайда іргелес матрица шамамен 2 бит жадты қолдана отырып, жадтағы графикті өте ықшам түрде ұсынады, бұл іргелес тізімдерден гөрі жақсы болуы мүмкін[5].
Іргелес тізім-бұл графиктің әр шыңы іргелес шыңдардың тізімі сақталатын жолға сәйкес келетін тізім. Мұндай деректер құрылымы қарапайым мағынада кесте емес, "тізімдер тізімі"болып табылады. Бұл сирек кездесетін графиктерді ұсынудың ең ыңғайлы тәсілі, сонымен қатар графикті ені мен тереңдігінде айналып өтудің негізгі алгоритмдерін орындау кезінде, сіз ағымдағы көрінетін шыңның "көршілерін" тез алуыңыз керек.

Қысқа жолды іздеу алгоритмдері
Қысқа жол туралы есеп-графиктегі екі нүктенің (шыңдардың) арасындағы ең қысқа жолды (тізбекті) табу міндеті, онда жолды құрайтын жиектердің салмақтарының қосындысы азайтылады[12].
Қысқа жол мәселесі графикалық теорияның маңызды классикалық міндеттерінің бірі болып табылады. Бүгінгі таңда оны шешудің көптеген алгоритмдері белгілі. Ең танымал қарастырайық.
Дейкстра алгоритмі - ең танымал және кең таралған алгоритм. Ол сондай-ақ ең қарапайым болып саналады[13]. Ол бірнеше шыңдары бар графиктерде жақсы орындалады. Графиктегі шыңдардың саны бірнеше мыңға жетуі мүмкін. Сонда бұл алгоритмді қолдану ең қысқа маршрутты табу мәселесін шешудің оңтайлы таңдауы болмайды. Алгоритмнің есептеу күрделілігі: 𝑂(𝑉2) [14].
Белман-Форд алгоритмі-бұл бір шыңнан басқаларына дейінгі жолды табатын өлшенген графиктен ең қысқа жолды табу алгоритмі [15]. Дейкстра алгоритмінен айырмашылығы, Белман-Форд алгоритмі графикте теріс салмағы бар жиектердің болуына мүмкіндік береді. Алгоритмнің есептеу күрделілігі: 𝑂 ( ∙ ∙ 𝐸).
Флойд-Уоршелл алгоритмі-өлшенген бағытталған графиктің барлық шыңдары арасындағы ең қысқа қашықтықты табудың динамикалық алгоритмі. Бұл алгоритмді едәуір тармақталған графиктегі есептерді шешуге қолданған кезде, ол есептеу машинасының ресурстары жағынан едәуір шығындарды талап етеді[16]. Алгоритмнің есептеу күрделілігі: 𝑂(𝑉3).
Қысқа маршрутты табу үшін біз қарапайым және ауыр емес болғандықтан, Дейкстра алгоритмін қолданамыз.

2.1. Графтардың байланысы
Анықтама 1. Егер G граф төбелерінің кез келген жұбы үшін байланыстырушы тізбек бар болатын болса, онда мұндай графты байланысқан граф деп атайды.
Графтардың қасиеттері:
:: Графтың əр төбесі тек бір ғана байланысу компонентіне
кіреді.
:: Кез келген аяқталған графта байланысу компоненттерінің
шектелген саны болады;
:: Тек жалғыз байланысу компонентінен тұратын граф
байланысқан граф болып табылады;
:: Графтың əр байланысу компоненті, оның ішкі графы
болып табылады;
:: Кез келген граф үшін не өзі, не оның қосымшасы
байланысқан болып табылады.

Қасиеттерді дəлелдеу.
4° жəне 5° қасиеттерді дəлелдейік.
G1 (V1,E1) - G (V,E) графының байланысу компоненті болсын. G графының G1 (V1,E1) компонентіне кірмейтін V2=V\V1 төбелер жиы- нын қарастырайық. Егер V2-ден барлық инцидентті қабырғаларымен бірге əрбір төбесін өшірсек, G (V,E) графының G1 (V1,E1) байланы- су компонентімен сəйкес келетін ішкі графын аламыз.
G (V,E) n-ретті кез келген граф болсын, ал G=(V,E) - оның Kn графына дейінгі қосымшасы. Граф байланысқан болғанда, пайым- дау айқын. G графы байланыспаған болсын, G1 (V1,E1) - оның байланысу компоненттерінің бірі жəне V2=V\V1. Онда кез келген v∈V1, w∈V2 төбелері үшін - G қосымшасында vw ∈ E қабырғасы бар. Сонда, V2-дегі кез келген төбе Е-ге жататын V1 қабырғаның кез келген төбесімен байланыстырылған, ал V1-дегі кез келген екі төбе, екі түйіні де E-де жатқан ұзындығы 2 болатын тізбекпен байланыстырылған. Сондықтан G графы байланысқан граф.
Графтың байланысуы графтың топологиялық сипаттамала- рының бірі. G графының төбелер байланысының саны (белгіленуі X(G)) төбелердің ең аз саны деп аталады, оларды өшіру (оған инцидентті қабырғалармен бірге) байланыспаған графқа немесе бір шеттетілген төбеден тұратын графқа алып келеді. Қабырғалық байланыс саны (белгіленуі λ(G)),G графының ең аз қабырғалар саны болып табылады, оны өшіру байланыспаған графқа алып келеді. Егер χ(G)=k жəне λ(G)=k орындалса, онда графы k-байланысқан деп аталады. G графының қосылуы бойынша, мак- сималды k-байланысқан ішкі граф k-байланыс компоненті деп ата- лады. Сəйкес графтардың байланыс санының коммуникациялық жəне логикалық желілерін зерттеуде сол желілердің сенімділік дəрежесі деп түсіндіруге болады.
Графтар теориясында байланысқан графтарды орнату тəсілдері зерттеледі. Олардың барысында k-байланысу немесе k-қабырғалы байланысу шарттары, əртүрлі байланыстар арасындағы қатынас, байланыс сандарының графтың өзге параметрлеріне тəуелділігі жəне т.с.с. зерттеледі. Сонда, егер δ(G) - G графының төбелерінің минималды дəрежесі болса, онда келесі теңсіздіктер дұрыс: χ(G)= λ(G)= δ(G). Кез келген a,b,c (0a=b=c) бүтін сандары үшін G графы бар, оның χ(G)=a λ(G)=b δ(G)=c. Егер G графының n төбелері бар жəне δ(G)=[n2] болса, онда λ(G)=δ(G). Егер u жəне v төбелері G-дан S жиынының элементтерін өшіру арқылы алынған G - S графының түрлі байланысу компоненттеріне жатса, онда S төбелер, яғни қабырғалар жиындары немесе n қабырғаларының төбелері u жəне v төбелерін бөледі.
Сонымен, келесі пайымдаулар дұрыс деп есептейміз. Көршілес емес u жəне v төбелерін бөлетін ең аз төбелер саны, u жəне v-ны байланыстыратын ортақ төбелері жоқ қарапайым тізбектердің ең көп санына тең. G графы, оның кез кел- ген төбелерінің жұбы ең болмағанда k-төбесі қиылыспайтын тізбектермен байланысқан жағдайда ғана k-байланысқан бола- ды. Ұқсас теоремалар қабырғалар арасындағы байланыс үшін де дұрыс келеді. Кез келген төбелерінің жұбы ең болмағанда k-қабырғалы қиылыспайтын тізбектермен байланысқан жағдайда ғана граф k-қабырғаларымен байланысады. Өшіру (жою) ба- рысында байланыспаған графқа əкелетін қабырғалар жиынын қиынды деп атаймыз. Əрбір графтағы u жəне v төбелерін бөлетін қабырғалары арқылы қиылыспайтын қиындылар саны көп болады, олар u мен v-ны байланыстыратын, яғни u жəне v-ның d(u,v) арақашықтығын байланыстыратын ең аз қабырғалар санынан тұратын қарапайым тізбекке тең.

Анықтама 2. Егер G графының бір-бірімен тізбектеп (қарапайым тізбек) байланыспаған бірнеше төбелер жұбы бар болса, онда ол граф байланыспаған граф деп аталады.
Байланыспаған графтың қарапайым мысалы ретінде оқшауланған төбелері бар графты айтуымызға болады.
Теорема. Графтың V төбелер жиынын, графтың кез келген қабырғасы ішкі жиынның біреуінің төбелерін байланыстыратын- дай екі бос емес V1 жəне V2 ішкі жиындарына бөлгенде ғана граф байланыспаған болып табылады.
Дəлелдеу. G(V,E) - байланыспаған граф болсын. Графтың кейбір v төбелерін нақтылап алып, оны v төбелерінен жəне оны- мен тізбектеп байланыстырған V төбелерінен тұратын V1 жиыны арқылы белгілейік. V1 жиыны бос емес (ең болмағанда v төбесінен тұрады) жəне V жиынымен сəйкес келмейді (V1=V графы G(V,E) - байланысқан, себебі оның кез келген екі төбесі арасындаарқылы өтетін тізбек бар). V2=VV1 қосымшасын қарастырайық.
V2 жиыны - бос емес жəне G(V,E) графының ешбір қабырғасы V1-дің бірде-бір төбесін V2-нің ешбір төбесімен байланыстырмай- ды. Сондықтан, алынып отырған V1 жəне V2 жиындары ізделініп отырған жиынын бөліктегеннен пайда болады.
Керісінше, теорема шартын қанағаттандыратын V жиыны V1∪V2 бөліктегенде пайда болсын.
G(V,E) графы байланыспаған граф екенін дəлелдейік. Əртүрлі жиындардан v∈V1 жəне w∈V2 ерікті төбелер жұбын алайық жəне осы төбелерді байланыстырушы тізбек бар деп есептейік. Мұндай тізбек, ұштары əр түрлі ішкі жиындарға жататын қабырғалардан тұрады, демек бұл шартқа қарама-қайшы. Теорема дəлелденді.
Егер w=v немесе басы v жəне соңы w болатын тізбек бар болатын болса, онда v төбелеріне қарасты графтың w төбесін алуға болады.
Теоремадан шығатын салдар.
G графы байланысқан болу үшін, ондағы кез келген нақтыланған төбелері арқылы сол графтың қалған барлық төбелерін алуымызға болатындығы жеткілікті.
Байланысқан граф, байланыспаған граф, байланысу компонен- ті, қасиеттері туралы тағы қайталап өтейік. Кез келген төбеден кез келген өзге төбеге жол бар болса, онда бағытталмаған граф байланысқан болады (жол қабырғалардың кез келген са- нынан тұруы мүмкін). Мысалы: төмендегі 2.1-суретте граф байланысқан болып табылады. Алайда, егер 4 жəне 5 төбелер арасындағы қабырғаны өшірсек, онда ол байланысқан болмайды - 5 төбесінен ешбір төбеге бару мүмкін болмайды.
Егер байланысу қасиеті орындалмаса, онда граф байланыспаған болады.
Ары қарай мультиграфтарды, яғни екі төбесі екі немесе одан да көп қабырғалармен байланысқан графтарды ескермей, тек қана төбелер жұбы бір ғана қабырғамен байланысқан немесе байланыспаған графтарды қарастырумен шектелеміз.
n төбелері бар граф байланысқан болу үшін, (n - 1) -ден кем емес қабырғалары болу керек.
Егер графта n * n − 3n + 4 кем емес қабырғалар болса, ол кепілді түрде байланысқан болады.
Егер граф байланысқан жəне циклсыз болса, онда оның кез
келген қабырғасын өшіру байланыстың жоғалуына əкеледі. Байланыспаған граф байланысу компонентінен тұрады. Бұл жиынның кез келген төбесі арқылы осы жиынның кез кел- ген төбесіне қатынаса алатын, бірақ бұл жиынның бір де бір төбелері осы жиыннан тыс кейбір төбелеріне қатынаса алмай- тын төбелер жиыны - байланысу компоненті болып табылады. Байланысу компонентінің төбелер саны граф төбелерінің саны- на тең екені айқын. Екі байланысу компоненттері
бар граф келтірілген.

Байланыс компоненті тек бір төбеден тұруы мүмкін екендігі айқын көрініп тұр. Егер графта n төбе бар болса, онда граф n-нан аспайтын байланысу компоненттерінен тұрады. Байланысқан графта байланысу компоненті жалғыз.
Байланыспаған графта кез келген байланысу компоненті n - 1 -ден аспайтын төбелерден тұрады. Егер графта k байланы- су компоненті бар екені анық болса, онда кез келген байланысу компоненті n - k + 1-ден аспайтын төбелерден тұрады.
Егер байланыспаған графта k-байланысу компоненті бар бол- са, онда байланысқан граф алу үшін, графқа кем дегенде k - 1 қабырға қосу қажет.
Графтың байланысқан екендігін қалай анықтауға болады?
Кейбір А төбесін таңдап алып, оны қатынас болған төбе ретінде белгілейміз (1), ал қалғандарын сəйкесінше қатынас болмаған төбе ретінде қарастырайық (0):
А-ны ағымдағы төбе деп алайық. Ары қарай келесідей əрекеттерді орындаймыз. Қаты- нас болмаған іргелес төбелерді белгілеу: ағымдағы төбе үшін, онымен əлі қатынас болмаған іргелес төбелерді іздейміз жəне содан соң оларды қатынас болған төбе ретінде белгілейміз.

Бізде k жаңадан белгіленген
төбелер пайда болсын (жоғарыдағы 2.3-суретте олардың саны - 3). Кезек бойынша олардың біреуін ағымдағы төбе деп аламыз жəне онымен қатынаста болмаған іргелес төбелерге рекурсивті
түрде белгілеулер жүргізіп, орындаймыз. Егер берілген төбелер арасында қатынас болған төбелер ретінде белгіленбеген іргелес төбелері болмаса, онда ағымдағы төбе үшін рекурсия орындал- майды.
Егер осы əрекеттерден кейін барлық төбелер қатынас болған төбе ретінде белгіленсе, граф байланысқан, басқа жағдайда байланыспаған болады.
Мұндағы төбедегі натурал сандар
қаншасыншы қатынастан соң қатынас болған төбе ретінде белгіленгендігін көрсетеді. Кез келген төбені таңдаймыз (1). Ары қарай, онымен үш көршілес емес төбелер белгіленеді (2, 3, 4). Ағымдық төбе (2) болады. Рекурсия: əлі қатынаспаған екі көршілес емес төбелерді белгілейміз
(5 жəне 6). (5) үшін рекурсия қажет емес - оның қатынаспаған көршілес төбелері жоқ, ал (6) үшін рекурсия қажет - (7)-ні белгілейміз. 7-ші нөмірде əлі қатынаспаған көрші - 8-ші нөмір бар, ал 8-ші нөмірде қатынаспаған көршілес төбелер жоқ. (2)-ден шыққан рекурсивті шақырулар аяқталды. Ендігі кезекте (3) төбе, бірақ мұнда рекурсия қажет емес, (4) төбе қалды. Оның көршілес төбелерінің бірі (9) əлі де белгіленбеген, оны ретке келтіреміз. Сонда:

Нəтижесінде шығатын қорытынды: кейбір төбелердің арасында қатынасу болмағандықтан граф байланыспаған болып табылады.

2.2. Маршруттар, жолдар, циклдар
Графтағы маршрут - əрбір i=1, 2, ..., n - 1 үшін xi жəне xi+1 төбелері қабырғамен байланысқан x1, x2, ..., xn төбелер тізбегі. Бұл n-1 қабырғалары маршрут қабырғалары деп аталады, марш- рут қабырғалары арқылы өтеді деп айтады, ал n-1санын маршрут ұзындығы деп атайды. Маршрут x1 жəне xn төбелерін байланыс- тырады дейді, оларды сəйкесінше маршрут басы жəне соңы деп
атайды, x2, ..., xn-1 төбелерін аралық деп атайды. Егер x1=xn болса, онда маршрутты тұйық деп атайды.
Жол - барлық қабырғалары əр түрлі болатын маршрут. Жол қа- рапайым деп аталады, егер оның барлық төбелері əр түрлі болса.
Цикл - бұл тұйық жол. x1, x2, ..., xn циклы қарапайым деп аталады, егер x1, x2, ..., xn-1 төбелері қосарланған əр түрлі болса.
2.6-суретіндегі графта төбелер тізбегі
2, 3, 5, 4 - маршрут емес;
2, 3, 4, 5, 1, 4, 3 - маршрут, бірақ жол емес;
3, 1, 4, 5, 1, 2 - жол, бірақ қарапайым емес;
2, 3, 1, 4, 3, 1, 2 - тұйық маршрут, бірақ цикл емес; 2, 3, 1, 4, 5, 1, 2 - цикл, бірақ қарапайым емес;
2, 3, 4, 5, 1, 2 - қарапайым цикл.
Маршруттың кейбір қарапайым қасиеттерін анықтайық.
Лемма 2.1. Екі əр түрлі төбені байла- ныстыратын кез келген маршрутта осы төбелерді байланыстыратын қарапайым жол болады. Кез келген қабырға арқылы өтетін кез келген циклда осы қабырға арқылы өтетін қарапайым цикл болады.
2.6-сурет
Дəлелдеу. x1, x2, ..., xn маршрут болсын.
Егер оның барлық төбелері əр түрлі болса, онда бұл қарапайым жол. Кері жағдайда xі=xj, ij. Онда осы маршруттан x1, x2, ..., xi-1, xi, xi+1, xn тізбегі. Жаңа маршрут сол төбелерді байланысты- рады жəне ұзындығы қысқа болады. Осылай əрекет істей оты- рып, соңғы түзету санынан кейін x1 жəне xn байланыстыратын қарапайым жол аламыз. Екінші тұжырым ұқсас дəлелденеді.
2.1.-леммадағы цикл сөзін тұйық маршрут сөзіне ауыстыруға болмайды. Шынымен, егер (a, b) - граф қабырғасы болса, онда a, b, a тізбегі - осы қабырға арқылы өтетін тұйық маршрут, бірақ онда цикл болмайды.
Лемма 2.2. Егер графта əрбір төбенің дəрежесі 2-ден кем болса, онда бұл графта цикл бар дегенді білдіреді.
Дəлелдеу. Графта ең үлкен ұзындықты қарапайым жол табайық. Бұл x1, x2, ..., xn болсын. xn төбесі xn-1 төбесімен сыбайлас, ал оның дəрежесі 2-ден кем болмағандықтан, ол ең болмағанда тағы бір төбемен сыбайлас, айталық у. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.