9-сыныпта факультатив сабағында векторлар ұғымы мен векторлық әдістің есептерді шешудегі қолданылуы


Курстық жұмыс
Қазақстан Республикасы Білім және Ғылым министрлігі
Академик Е. А. Бөкетов атындағы Қарағанды университеті
Математика және ақпараттық технологиялар факультеті
Математиканы және информатиканы оқыту әдістемесі кафедрасы
КУРСТЫҚ ЖҰМЫС
Пәні: Сыныптан тыс жұмыс (факультативтік сабақ)
Тақырып: Математикадан факультатив сабағында векторлар туралы түсінік және векторлық әдісті есептерді шығаруда қолдану (9 сынып)
Орындаған: МиИ-423 топ студенті Аппақ Г. Е.
Тексерген: Ахманова Д. М.
Қарағанды, 2021
МАЗМҰНЫ
1. ВЕКТОРЛАР ТУРАЛЫ ТҮСІНІК
1. 1 Векторлар ұғымы және оның шығу тарихы
1. 2 Векторларды жіктеу тәсілдері
2 ВЕКТОРЛЫҚ ӘДІСТІ ЕСЕПТЕРДІ ШЫҒАРУДА ҚОЛДАНУ
2. 1 Алгебралық есептерді шешуде векторлық әдісті қолдану
2. 2 Планиметриялық есептерді шығаруда қолдану
2. 3 Стереометриялық есептерді шығаруда қолдану
ҚОРЫТЫНДЫ
ӘДЕБИЕТТЕР ТІЗІМІ
ҚОСЫМША
Кіріспе
Еліміздің егемендікке ие болып, Қазақстан өз алдына мемлекет мәртебесіне жетіп бүкіл әлемге, жер жүзіне өзінің елдігін, саясатын танытатын шаққа жетіп отыр. Еліміздің елдігін танытып, оны жетілдіріп, дамытатын жас ұрпақ сондықтан да еліміздің болашағы жас жеткіншектің білім дәрежесінің тереңдігімен өлшенеді.
Сондықтан адал ниет жас жеткіншектерге білім мен тәрбие есігін ашу мектеп мұғалімдеріне абыройлы да жауапты жұмыс жүктейді. Өйткені білім тәрбиенің негізі, демек баланың жеке басының қалыптасу кезеңі мектеп қабырғасында қаланады.
Математиканы оқытудың білімдік мақсаты барлық оқушыларды математика ғылыми негіздері туралы жүйелі білімдермен және оларды толық, сапалы да берік игеруге қажетті біліктіліктермен, дағдылармен қаруландыру болып табылады. Осындай білім алу нәтижесінде оқушылардың ақыл-ойы дамиды.
Геометрия курсы қандай жолмен құрылмасын онда міндетті түрде теоремаларды дәлелдеудің, есептерді шығарудың әртүрлі әдістері қарастырылады. Олардың ішінде векторлық әдіс, координат әдісі және геометриялық түрлендірулер әдісі ерекше орын ала¬ды. Бұл әдістер өзара тығыз байланысты.
Геометрияның теориясын дәлелдеу мен есептерін шешудегі барынша тиімді әдістердің бірі -векторлық әдіс. Есептерді жалпы түрде шешуде де векторлардың атқаратын мәні зор. Бұл жөніндегі көптеген теориялық мәселелер мазмұнында теория тікелей қолданатын есептермен қосарланып баяндалу керек. Теориялық тұжырымдарды қолданып есептер шеше алған оқушы ғана сол оқу материалын меңгере алады.
Курстық жұмыстың өзектілігі: Вектор ұғымы орта мектептің геометрия оқулығында 9-10 сыныптарда оқытылады. Геометрия курсында векторлар тақырыбына аз уақыт беріледі. Болашақ математика мұғалімі математиканы оқытудың жалпы заңдылықтарын, әдістемелік зерттеулерді, оқытудың әр түрлі әдіс-тәсілдерін, есептер шығаруда қолдана білуді қажет етеді. Есептерді шығаруда векторлық әдісті қолдану тақырыптың өзекті мәселесі болып отыр.
Курстық жұмыстың мақсаты: Математика курсындағы есептерді шығаруда векторлық әдісті пайдаланып шешудің әдіс- тәсілдерін үйрету.
Оқушылардың теорияда алған білімдерін, ақыл-ой белсенділігін, шығармашылық қабілеттерін, дағдыларын қалыптастыру және ойлау қабілеттерін дамыту.
Курстық жұмыстың міндеттері:
-векторлық әдіс пен координат әдісі арасындағы байланысты зерттеу;
-векторлық әдісті нақтылы теорияға сүйене отырып, есептер шығару барысында дәлелдеу.
Зерттеу нысаны: Мектеп математикасын оқытуда векторлық әдісті есептерді шығаруға қолдану.
Курстық жұмыстың жаңалығы: Оқушыларды математика курсы бойынша алған теориялық білімін, дағдыларын қалыптастыру және өз бетімен алған білімін практикада тиімді пайдалану.
Зерттеу жұмысының әдістемелік негіздері: Қазақстандық мектептердi жаңарту тұжырымдамасы жалпы бiлiм берудiң басым бағыттарын айқындайды, бұл басым бағыттар мектепте бiлiм берудi дамытуға негiз болады. Математика сабағында оқушылардың шығармашылық логикалық ойлау қабілетін дамытуға бағытталған дидактикалық бірліктерді ірілендіру әдісі пайдаланылса, онда оқушыларың танымдық қызығушылығы артады, білімді игеру сапасының деңгейі жоғарылайды.
Курстық жұмыстың практикалық құндылығы: бұл тақырып бойынша есептер қарастылды және олардың шығару үлгілері көрсетіліп, тиімділігі түсіндіріледі.
Мектептің математика пәнінің мазмұнының күннен-күнге күрделене түсуі, көлемінің өсуі және өзгеріске ұшырауы, оған бөлінетін уақыт мөлшерінің жылдан жылға кемуі мен пән мазмұнын оқушылардың аз уақыт ішінде шығармашылықпен қарқынды меңгерулерінің қажеттілігі арасында қарама-қайшылық туындап отыр. Сондықтан математиканы оқыту процесінде шығармашылық тапсырмаларды қолдану әдісі арқылы оқушылардың шығармашылық қабілетін дамытуды ғылыми-әдістемелік тұрғыда көкейкесті мәселе болып табылады.
1 ВЕКТОР ТУРАЛЫ ТҮСІНІК
- Векторлар ұғымы және оның шығу тарихы
Қазіргі заман математикасының негізгі де ілгерлі ұғымдарының бірі - векторлық кеңістік ұғымы. Бұл ұғым математканың сызықтық алгебра, сызықтық программалау, функционалдық анализ және физиканың толып жатқан салаларында қолданылады.
Векторлар теориялық физикада, механикада, гидродинамикада, аэродинамикада, потенциалдар теориясында, қолданбалы математикада, химияда, экономикада табысты қолданыс тауып отыр. Векторлық аппарат қазіргі заман математикасында қолданумен шектелмей, жоғары оқу орындарында оқытылатын техникалық, математикалық пәндердің оқулықтарында лайықты орын алды. Векеторлық аппаатың атқаратын ролінің маңыздылығы соншалық - аталмыш курстар векторлардың өздеріне қажетті тарауларын толығымен қамтиды. Дифференциалдық геометрия, аналитикалық геометрия, математикалық физика, теорялық физика векторлар негізінде баяндалады.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық аппарат көмегімен шешіледі. Компьютерді дифференциалдық геометрия, аналитикалық геометрия, математикалық физика, теорялық физика векторлар негізінде баяндалады.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық аппарат көмегімен шешіледі. Компьютерді падаланып, дененің кескінін жасау үшін векторлық графика пайдаланылады. Сызықтық программалауда вектордың көмегімен толып жатқан практикалық мәселелер шешіледі. Мәселен, өндіріс орнының ең тиімді жұмыс кестесін жасау, жүк тасымалдаудың ең пайдалы әдісін іздеп, табу; матаны, қаңылтырды, тағы да сол сияқты заттарды кесіп-пішудің үнемді әдісін - міне осы сияқты мәселелер.
"Математикалық эконмика" деп аталатын экономиканың саласында векторлардың көмегімен қарастырылады. Қазіргі кезде өндіріс орнының қуатын вектор түрінде өрнектеу аса қолайлы болып отыр. Векторлар қолдануларға өте бай.
Векторлық есептеулер математиканың жас салаларның бірі екендігіне қарамастан, өзінің маңыздылығының арқасында, қолдану ауқымның кеңдігі арқасында кейінгі елу - алпыс жыл шамасында көптеген елдерде мектеп математикасына еніп, оның құрамдас бөлігі болып, орнығып алды. Векторлар мектептерімізде оқытыла батағанына ширек ғасырдан артық уақыт болды. Бірақ, мұғалімдерге қажетті тарихи-әдістемелік материалдар әзірше дайындалмаған. Абстрактылығы жоғары векторларды оқушыларға саналы да терең меңгерту үшін, олардың векторларды оқып-білуге деген ынтасын арттыру үшін тарихимағлұматтар бере отырудың маңызды екендігі сөзсіз, Математика слінінің мұғалімдері векторлық есептеулердің жасалу тарихын, векторлардың қолдануларын, ғылым және техника салаларындағы маңызын білгендері абзал. Жоғарыда айтылғандарды ескере келе, мұғалімдердің пайдалануына арнайы дайындалған, векторлық есептеулердің жасалу тарихының қысқаша мазмұнын төменде беріп отырмыз.
Техника ғылымдардың қауырт дамуына байланысты он сегізінші ғасырдың өзінде-ақ есептеу аппаратын жетілдірудің қажет екендігі байқалды. Бұрыннан қолданылып келегн есептеу түрлері ендігі жерде қажеттілікті қанағаттандыра алмайтын болып шықты. Теориялық физиканың жедел де аса күшті қарқынмен дамуына байланысты он тоғызыншы ғасырдың басныда математикалық аппаратты жетілдіруге деген талап күшейе түсті. Есептеудің талапқа сай жаңа түрін іздестіру қажет болды. Нәтижесінде он тоғызыншы ғасырдың екінші жартысында веторлық есептеулер дүниеге келді де, үлкен қарқынмен тез дамыды және математиканың құрамдас бір бөлігі болып қалыптасты.
Векторлық есептеулерді жасауға көптеген елдердің толып жатқан ғалым - математикатері мен физика- механиктері, инженер-техниктері қыруар үлес қосты. Векторлық есептеулердің жасы "жас" болғанымен бастау көзі сонау ерте заманда өмір сүрген данышпан Аристотельдің Механикалық проблемалар атты еңбегінде табылды. Аристотель осы еңбегінде бір нүктеге түсірілген және де өзара бұрыш жасай бағытталған екі күштің әсерінен дененің жүрген жолын табуды екінші мәселе етіп қояды. Оның жиырма төртінші мәселесінің мазмұны төмендегідей:
Ромбтың қабырғасының бойымен бірі-бірімен қарама-қарсы бағытта екі нүкте бірдей жылдамдықпен қозғалып келеді. Ромбтың қабырғасы дәл сондай жиырма төртінші мәселесінің мазмұны жылдамдықпен қарсы жатқан қабырғаға қарай қозғалады. Әр нүктенің жүрген жолы қандай?
Жауап: Әр нүкте ромб диаогналі бойымен қоғалады.
Сұрақ: бірдей жылдамдықпен қозғалып келе жатқан нүктелер бірдей уақытта неге әртүрлі жол жүреді?…
Міне осыдан Аристотельдің
- қозғалыстарды (орын ауыстыруларды) қосуға параллелограмм ережесін қолданғандығы.
- векторлардың геометриялық қосындысн табудың қазіргі, біз қолданып жүрген түріне өте жақын келгендігі анық байқалады.
Он жетінші ғасырда Аристотельдің "қозғалыстар параллелограмы" қайтадан жанданды. Галилео Галилей (1564-1642) күш және оның денені қозғайтын құраушысының арасындағы метрикалық байланысты зерттеді. Оның еңбектеріне қарап, Галилейдің "теңәсерлі күш", "қорытқы " жылдамдық" ұғымдарына өте жақын, қапталдас келгенін көруге болады. Ағылшын математигі, әрі физигі атақты Исаак Ньютон (1643-1727) қозғалыстарды қосуға алғаш рет "параллелограмм" ережесін пайдаланды. Неміс математигі Готфрид Вильгельм Лейбниц (1646-1716) "геометриялық есептеулер" идеясын берді, оны әрі қарай дамытпады.
Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис (1616-1703) механикаға геометриялық аппарат жасап беруде жаңа әрі аса ірі қадамжасады. Ол екі, үш күштің тең әсерлі және қорытқы күшін табуға, қорытқы жылдамдықты табуға қолданылатын параллелограмм ережесін ғылымға салғаш жасады. Ол екі, үш күштің тең әсерлі және қорытқы күшін табуға, қорытқы жылдамдықты табуға қолданылатын параллелограмм ережесін ғылымға алғаш енгізген Джон Валлис болды. Күштерді, жылдамдықтарды қосу, жіктеу; векторды санға көбейту амалдарын алғаш берген де осы адам. Сөйтіп, Джон Валлис механикада векторлық алгебраның негізін қалаған оқымысты болды. Он сегізінші ғасырда математика мен механикада аналитикалық әдістерімен әуестенубасым болды. Леонард Эйлер (1707-1783) мен Лагранждың арқасында механика математиканың жаң бір саласы болатын жағжайға жеткізілді. Тек қана он сегізінші ғасырдың ақырғы кезінде Монждың (1746-1816) геометрия мектебінде геометриялық әдістерге қайта оралуға деген ұмтылыс байқалды. Әсіресе кинематикадағы қозғалыстарды зерттеуге геометриялық әдіс аса тиімді болып шықты, Л. Карно бұл бағытта аса табысты еңбек етті. Ол "Қозғалыстың геометриялық теориясын" жасау мәселесін көтерді, векторды қосудың "көпбұрыш ережесін" және қазір пайдаланып жүрген векторлық есептеудің символдық аппаратын жасап шықты. Множ-Понселе мектебінің көрнекті өкілі Баре де Сен-Венан (1797-1886) серпімділік теориясындағы, гидродинамикадағы, термодинамикадағы, жалпы механикадағы тамаша еңбектерімен физиктер мен механиктер ортасында аса танымал тұлға еді. Сен-Венан векторлық есептеулер саласында да қомақты үлес қосты. Механикада қолданылатын векторлық аппаратты жетілдіруде жемісті еңбек етті, векторлық аппаратты әрі қарай дамытты. "Об геометрических суммах и разностях и их применение для упрощения механики" атты 1845 - жылы Жарияланған еңбегінде Сен-Венан скаляр көбейтінді, векторлық көбейтінді, ветор функцияны дифференциалдау, интегралдау ережелерін берді. Сөйтіп, ол механиканы вектор негізінде құрудың жалпы схемасын жасап шықты. Понселенің шәкірті Резаль (1820-1896) 1862- жылы жарияланған "Чистая кинематика" еңбегінде Сен-Венан жасаған векторлық апаратты жетілдіре түсті және векторлық апараттың кинематикада қолдануларына толып жатқан мысалдар көрсетті.
Векторлық есептеулердің негізін салушылар Ирландия математигі әрі астрономы Уильям Гамильтон (1805-1865) және неміс математигі Герман Грассман (1809-1877) деп айтылып жүр.
1844- жылы Уильям Гамилтонның векторлық есептеулерге арналған алғашқы мақалалары және Герман Грассманның " Учение о протяженности" атты көлемді еңбегі жарияланды. 1853-жылы Гамильтонның "Лекции о кватернионах" атты еңбегі жарық көрді. Бұлардың әрқайсысы есептеудің жаңа әрі әмбебап түрін жасамқшы болды, векторлық есептеулерге қыруар еңбек сіңірді. " Вектор ұғымын "1846-жылы ғылымға енгізген Гамильтон болды. Векторлық есептеулердің негізін салушылар деп Гамильтон мен Грассманды айтатындар баршылық. Бірақ аталмыш еңбектермен бір кезде дерлік жарық көрген Сен-Венанның мемуарлары идея жағынан да, мазмұн жағынан да Гамильтонның кватерниондар алгебрасына да, Грассманның геометриялық анализіне де тәуелсіз, әрі өте құнды еңбек болып табылады. Д. Валлис, Л. Карно, Сен-Венан, резаль бұлар векторлық алгебра мен векторлық анализдің ұғымдарын ғылымға енгізді, механикаға қажетті геометриялық аппарат жасау жолында ғылымға енгізді, механикаға қажетті геометриялық аппарат жасау жолында жемісті еңбек етті. Есептеудің жаңа түрі бойынша жинақталған бай, мазмұнды материалды ортақ бір идея бойынша біріктіріп, механикалық "тұғырынан" ажыратып, бұл апаратты математикалық пән дәрежесіне көтеру керек болды. Осыны Санкт- Петербург университетінің профессоры Иосиф Иванович Сомов (1815-1876) өзінің 1864-жылы жарық көрген "Об ускарениях различных порядков", деп аталатын еңбегінде абыроймен орындап шықты. Жоғарыда аттары аталған, векторлық есептеулерді жасауға еңбек еткендердің негізгі көпшілігі векторлық аппаратқа инженер көзімен қараса, И. И. Сомов математика көзімен қарады. Ол векторлық есептеулерді математикалық пән дәрежесіне көтерді.
Векторлық есептеулерді және олардың тамаша қолдануларын дамытуға И. И. Сомовтан басқа да орыс және Кеңес ғалымдарының қосқан үлкен үлесі болды. Осы тұрғыда атақты математик Санкт-Петербург академиясының академигі М. В. Остроградскийді (1801-1916) және П. А. Котельников, А. Л. Фридман, Н. Е. Кочин, Я. И. Френкель (1894-1952), П. А. Широков (1895-1944), Д. И. Зейлиегер (1864-1936) сияқтыларды атаған жөн.
1. 2 Векторларды жіктеу тәсілдері
Векторларды координаттық осьтер бойынша жіктеу
Егер вектордың абсолют шамасы бірге тең болса, оны
бірлік вектор
деп атайды. Бағыты координаттың оң жарты осьтердің бағытындай бірлік векторлар
координаттық векторлар
немесе
орттар
деп аталады. Біз оларды
х
осі бойында
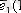 және
у
осі бойында
және
у
осі бойында
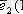 деп белгілейміз.
деп белгілейміз.
Ал координаттың векторлар нөлдік вектордан өзге және де коллинеар емес болатындықтан, кез келген
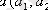 векторды осы векторлар бойынша жіктеуге болады:
векторды осы векторлар бойынша жіктеуге болады:
 (*)
(*)
Осы жіктеудің
 мен
мен
 коэффициенттерің табамыз. Ол үшін (*) теңдіктің екі жақ бөлігін де
коэффициенттерің табамыз. Ол үшін (*) теңдіктің екі жақ бөлігін де
 векторына көбейтеміз. Сонда
векторына көбейтеміз. Сонда
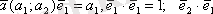 , ендеше
, ендеше

(*) теңдіктің екі жақ бөлігін де
е
2
векторына осылайша кебейтіп,
 екенін табамыз.
екенін табамыз.
Сонымен, кез келген
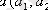 векторды былай жіктеуге болады:
векторды былай жіктеуге болады:
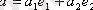
Сондықтан, егер
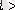 болса, онда
В
нүктесі
ОА
жарты түзуінде жатады, ал одан болса,
болса, онда
В
нүктесі
ОА
жарты түзуінде жатады, ал одан болса,
 мен
мен
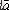 векторлары бірдей бағытталады. Егер де
векторлары бірдей бағытталады. Егер де
 болса, онда
В
нүктесі толықтауыш жарты түзуде жатады да,
болса, онда
В
нүктесі толықтауыш жарты түзуде жатады да,
 мен
мен
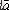 векторлары қарама-қарсы бағытталады.
векторлары қарама-қарсы бағытталады.
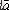 векторыньщ абсолют шамасы мынаған тең:
векторыньщ абсолют шамасы мынаған тең:
Теорема дәлелденді.
Есеп.
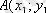 мен
мен
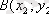 нүктелері берілген. Сонда АВ мен
ВА
векторларының қарама-қарсы бағытталғанын дәлелдеңдер.
нүктелері берілген. Сонда АВ мен
ВА
векторларының қарама-қарсы бағытталғанын дәлелдеңдер.
Шешуі.
АВ
векторының коордннаттары
 мен
мен
 болады.
ВА
векторының координаттары
болады.
ВА
векторының координаттары
 мен
мен
 болады. Біз мынаны көріп отырмыз:
болады. Біз мынаны көріп отырмыз:
 . Олай болса, АВ мен
ВА
векторлары қарама-қарсы бағытталған болып шығады.
. Олай болса, АВ мен
ВА
векторлары қарама-қарсы бағытталған болып шығады.
Векторды коллинеар емес екі вектор бойынша жіктеу
Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталадығ Коллинеар векторлар не бірдей багытталган болады, не қарама-қарсы бағытталған болады.
Айталық,
 мен
мен
 - нолден өзге коллинеар векторлар болсын. Сонда
- нолден өзге коллинеар векторлар болсын. Сонда
 саны табылып
,
саны табылып
,
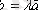
теңдігі орындалатынын дәлелдейік .
Айталық,
 мен
мен
 векторлары бірдей багытталған болсын. Сонда
векторлары бірдей багытталған болсын. Сонда
 және
және
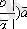 векторлары да бірдей бағытталған және олардың абсолют шамасы
векторлары да бірдей бағытталған және олардың абсолют шамасы
 да бірдей болады. Демек. олар тең:
да бірдей болады. Демек. олар тең:
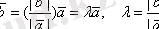
 мен
мен
 векторлары қарама-қарсы бағытталған болғанда былай тұжырымдаймыз:
векторлары қарама-қарсы бағытталған болғанда былай тұжырымдаймыз:

дәлелдемекшіміз де осы болатын.
Айталық,
 мен
мен
 - нөлден өзге коллинеар емес векторлар болсын. Енді кез келген
- нөлден өзге коллинеар емес векторлар болсын. Енді кез келген
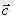 векторды
векторды
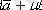
түрінде көрсетуге болатынын дәлелдейік.
Айталық,
А
мен
В -
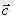 векторының басы мен ұшы болсын.
А
мен
В
нүктелері арқылы
векторының басы мен ұшы болсын.
А
мен
В
нүктелері арқылы
 және
және
 векторларына параллель түзулер жүргіземіз. Олар қандай да бір
С
нүктесінде қиылысады. Сонда:
векторларына параллель түзулер жүргіземіз. Олар қандай да бір
С
нүктесінде қиылысады. Сонда:
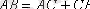
 мен
мен
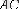 векторлары коллинеар болғандықтан,
векторлары коллинеар болғандықтан,
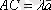 болады.
болады.
 мен
мен
 векторлары коллинеар болгандықтан,
векторлары коллинеар болгандықтан,
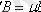 болады. Сонымен,
болады. Сонымен,
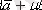 дәлелдемекшіміз де осы болатын.
дәлелдемекшіміз де осы болатын.
Векторлардың скаляр көбейтіндісі
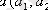 мен
мен
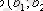 векторларының
скаляр көбейтіндісі
деп
векторларының
скаляр көбейтіндісі
деп
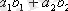 санын атайды.
санын атайды.
Векторлардың скаляр көбейтіндісін де, сандарды көбейткендегідей, жазып орындайды,
 скаляр кебейтінді
скаляр кебейтінді
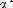 деп атайды.
деп атайды.
2 ВЕКТОРЛЫҚ ӘДІСТІ ЕСЕПТЕРДІ ШЫҒАРУДА ҚОЛДАНУ
2. 1 Алгебралық есептерді шешуде векторлық әдісті қолдану
Вектор ұғымы - физикалық ұғым ғана емес, математикалық ұғым. Математикада еркін вектор ұғымы қолданылады. Векторларға қолданылатын амалдардың ішінде байы - скаляр көбейтінді амалы. Ол алгебрада теңсіздіктерді, теңдеулерді, теңдеулер жүйесін шешуде қолданылады.
Қазіргі кезеңде мектеп математикасын оқытуда есеп шығаруға оқу уақытының басым бөлігі арналады. Бұған қарамастан оқушылардың көпшілігі есептерді дәстүрлі емес тәсілдермен шығаруға қиналады. Бұл келеңсіз құбылыстың басты себебі, мектеп оқулықтарының негізгі тарауларындағы есептер шешу әдісі оқушылардың бағдарламадағы материалдардың бір сұрағына ғана жауап бере алатындай білім, біліктілік және дағдыны қажет ететін бір тақырып шеңберінде қарастырылған. Есептердің көпшілігі мектеп математика курсының әртүрлі тарауларының арасындағы өресі кең байланыстар мен қатынастарды қамтымайды. Мұндай есептердің рөлі мен маңызы айтарлықтай бола алмайды, қызмет көрсетуі ұзаққа созылмайды, көбінесе олардың міндеті бағдарламадағы теориялық сұрақтарды түсіндірумен шектеледі. Сондықтан ондай есептерді қандай әдіспен шығаруы керектігі көп жағдайда белгілі болады. Ол әдістерді өтілетін материал тақырыбы, оқулық немесе есептер жинағының тарауларының аты, мұғалім бағдары және т. б. өзі ақ тұспалдап айтып береді, яғни қажетті әдісті іздеу қиын [8] .
Мысал келтірейік. ХІ сыныпта өзіндік жұмыс ретінде «Теңсіздіктер» тақырыбына мынадай есеп ұсынылады.
Есеп
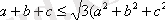 ( мұндағы a, b және c нақты сандар) теңсіздігін дәлелдеңдер.
( мұндағы a, b және c нақты сандар) теңсіздігін дәлелдеңдер.
Алдымен, берілген теңсіздікті дәстүрлі тәсілмен дәлелдеу мәселесіне тоқталайық.

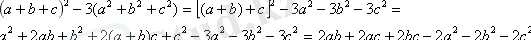
1-жолы
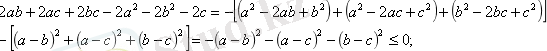
Кез келген a, b және c нақты сандары үшін.
2-жолы

өрнегіндегі әріптердің біреуін ғана айнымалы деп қабылдап, ал қалғандарын тұрақтылар деп есептеп, мысалы, берілген өрнекті а айнымалысына тәуелді (онда b және c тұрақтылар болады) квадрат үшмүшелік деп қарастырамыз:
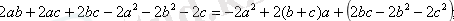
Бұл квадрат үшмүшеліктің бірінші коэффициенті 2-ге тең болғандықтан оның графигі параболаның тармақтары төмен қарай бағытталған. Енді оның дискриминантын табамыз:
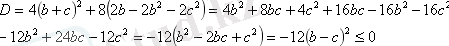
Демек кез келген b, c нақты сандар үшін
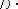 болады. Ендеше кез келген a, b және c нақты сандары үшін
болады. Ендеше кез келген a, b және c нақты сандары үшін
 теңсіздігі орындалады.
теңсіздігі орындалады.
Сонымен, ең соңында теңсіздігінің орынды болатындығы тағайындалды. Осыдан келіп берілген теңсіздіктің де кез келген a, b және c оң нақты сандары үшін ақиқат екендігіне көз жеткізуге болады.
Онан соң берілген теңсіздікті дәстүрлі емес тәсілмен, атап айтқанда векторлық тәсілмен дәлелдеуді іске асыруды қарастырайық.
Бұдан әрі кез келген
 және
және
 векторларының скаляр көбейтіндісі үшін қандай векторлық теңсіздіктің орындалатындығын ескереміз:
векторларының скаляр көбейтіндісі үшін қандай векторлық теңсіздіктің орындалатындығын ескереміз:

теңсіздіктің кез келген
 және
және
 векторлары үшін ақиқат екендігі белгілі.
векторлары үшін ақиқат екендігі белгілі.
Бұдан әрі біз
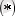 теңсіздікті
теңсіздікті
 және
және
 векторларының координаталары бойынша жазсақ, онда оның мына түрге
векторларының координаталары бойынша жазсақ, онда оның мына түрге
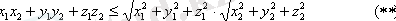
келеді және біздің жағдайымызда
 ,
,
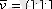 болғандықтан, болуы себепті, соңғы
болғандықтан, болуы себепті, соңғы
 теңсіздіктен дәлелдеуге берілген
теңсіздіктен дәлелдеуге берілген
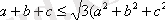 теңсіздігінің ақиқат екендігіне көз жеткіземіз.
теңсіздігінің ақиқат екендігіне көз жеткіземіз.
Көріп отырғанымыздай, берілген теңсіздікті стандарт тәсілмен дәлелдеуге қарағанда оны векторлық тәсілді пайдаланып дәлелдеу әрі қысқа әрі жеңіл.
Мысалдар келтірейік.
Есеп
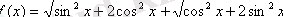 функциясының ең үлкен мәнін табыңдар.
функциясының ең үлкен мәнін табыңдар.
- Есепті түсіну, ұғыну.
Есеп мазмұнына талдау жасаймыз. Берлігені: f(x) функциясы, оның анықталу облысы барлық нақты сандар жиыны R. Табу керек: f(x) функциясының ең үлкен мәні.
- Есепті шығару жоспарын құру.
f(x) -тің ең үлкен мәнін қалай табуды білмегендіктен, оның квадратының ең үлкен мәнін, яғни
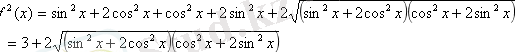
есепті шығарудың толық жоспары құрылады:
- теңдеуін шешу арқылы тің максимум нүктесін табу;
- f2(x) тің ең үлкен мәнін табу;
- f(x) -тің ең үлкен мәнін табу;
Осы қадамдарды орындау арқылы f(x) -тің ең үлкен мәнін табуға болатындығына оқушылардың көздері жетеді
- Құрылған жоспарды жүзеге асыру. Құрылған жоспарды жүзеге
асыру енді онша қиындық көрсетпейді. Жоспарда аталып көрсетілген сатылардағы амалдарды тізбектей отырып, f(x) -тің ең үлкен мәнін оңай табамыз:

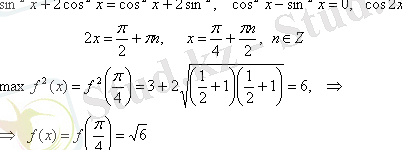
- Шешімді қайта қарау, тексеру.
Сонымен
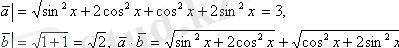
болғандықтан,
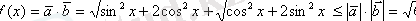
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz