Теңсіздікті шешу тәсілдері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 51 бет
Таңдаулыға:

Кіріспе

I. Трансценденттік теңсіздіктерді шешудің теориялық негіздері

1. 1 Бір айнымалысы бар теңсіздіктерді шешумен байланысты негізгі ұғымдар.

1. 2 Теңсіздікті шешу тәсілдері.

1. 3 Көрсеткіштік теңсіздіктерді шешу әдістері .

1. 4 Логарифмдік теңсіздіктерді шешу әдістері.

1. 5 Тригонометриялық теңсіздіктерді шешу әдістері.

II. Трансцендентті теңсіздіктерді шешу әдістерін оқыту.

2. 1 Теңсіздіктерді оқыту әдістемесі.

2. 2 Күрделілігі жоғары трансцендентті теңсіздіктерді шешудің дәстүрлі емес тәсілдерін оқыту әдістемесі .

2. 3 Трансцендентті теңсіздіктерді шешуге берілген есептерді шығару

Кіріспе

Қоғам дамуының республикамызда орын алып отырған әлеуметтік экономикалық бағыттары және жас ұрпақты ғылыми - техникалық прогресс және қазіргі заман талабына сай оқыту мен тәрбиелеу формасы, оқыту мақсатын, мазмұнын, түрін, әдістерін қайта қарап, оқу процесіне көптеген өзгерістер енгізуді қажет етеді. Білім саласындағы мемлекеттік саясаттың тұжырымдамасында: «бұл саланы реформалаудың стратегиялық нысаны мүлде жаңаша, шығармашылық тұрғыда ойлап алатын, танымдық мәдениеті биік адамдардың жаңа легін, дүниеге ғылымилық тұрғыдан жоғары жауапкершілігіне қарай білетін, біліктілігі жоғары мамандарды қалыптастыру идеясы болуға тиіс» - деп көрсетілген болатын.

Осыған байланысты орта мектептерде математиканы оқыту әдістері оқу процесінің санасын жоғарылату, оқушылардың танымдық мүмкіндіктерін белсенді түрде дамыту, білімнің мазмұнын толықтырып жетілдіру бағытында жаңартылуда. Еліміздегі білім жүйесі дүние жүзілік білім кеңістігіне біріге бастауына орай, білім мазмұнының мақсатты компоненттері өзгеруде.

Математикалық білім берудегі тереңдете түсудегі негізгі құралдардың бірі оқушылардың әр түрлі математикалық есептер мен жаттығуларды өз бетінше орындауына басшылық ету және оны тиімді ұйымдастыра білу болып табылады. Оқушылардың математикалық даму дәрежесі олардың есеп шығара білуінен анық байқалады. Есеп - әрбір мектеп оқушыларының ақыл - ойын дамытудың негізгі құралы.

Есептер шығару процесінде оқушылардың бағдарламадағы талаптарға сай математикалық білімін, шеберліктерін, дағдыларын жүйелі түрде қалыптастыруға және олардың шығармашылық белсенділігін, ізденімпаздық қабілеттерін арттыруға болады. Оқушының математикалық білімін көтерудің ең басты алғы шарты оның пәнге деген қызығушылығын арттыру. Пәнге деген қызығушылық болса бала оған көңіл қойып, тыңдап, тереңдете оқып үйрене бастайды.

Трансцендент сан - бүтін коэффициентті көпмүшеліктің түбірі болып табылмайтын нақты немесе жорамал сан.

Трансцендент сандарын алғаш рет француз математигі Ж:Луивилль (1809-1882) енгізді. 18 ғ-дың ортасында е, π, In2, 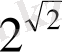, т. б. түріндегі сандардың трансцендент сандар екендігі белгісі болса да, ол ұзақ уақыт дәлелденбеді.

Трансценденттік теңдеу - құрамында белгісіз (айнымалы) шамалардан тәуелді трансценденттік функциясы болатын теңдеу. Мысалы: sinx+Igx=x, 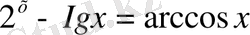. Жуықтап шешуден басқа жалпы түрде шешу жолы жоқ болғандықтан, әдетте трансцендент теңдеулерді көрсеткіштік, логарифмдік және тригонометриялық теңдеулер түрінде қарастырады.

Трансценденттік теңсіздік деп - құрамында белгісізі трансценденттік функцияның айнымалысы болып келетін теңсіздікті айтамыз. Ал, трансценденттік функция деп алгебралық емес аналитикалық функцияны айтамыз. Мұндай функцияларға мысал ретінде логарифмдік, көрсеткіштік және тригонометриялық функция қарастырамыз. Егер трансценденттік функцияны комплекс айнымалысы бар функция ретінде қарастыратын болсақ онда трансцендентті функцияның басқа функциялардан өзіндік ерекшелігі бар. Мысалы $е^{z}, \ \ sinz$ функцияларының ерекше нүктесі болады: z= $\infty$

Трансценденттік теңсіздікті шешудің біріңғай жалпы әдісі жоқ. Әдетте мектеп бағдарламасында трансцендентті теңсіздіктің қарапайым түрлері қарастырылады, атап айтсақ: логарифмдік, көрсеткіштік, тригонометриялық, кері тригонометриялық, көрсеткіштік теңсіздіктер.

Ғылыми жұмыстың мақсаты трансцендентті теңсіздіктерді шешудің дәстүрлі әдістерінен басқа да әдістерін қарастыра отырып, оларды оқытудың әдістемесін ұсыну. Мұнда дәстүрлі әдіс деп потенцирлеу әдісі, негізгі тепе теңдіктерді қолданып қарапайым теңсіздіктерге келтіру, жаңа айнымалы енгізу әдісі, интервалдар әдісі және графиктік әдістерді айтсақ, дәстүрлі емес әдістер деп рационализациялау әдісі, туындының көмегімен теңсіздікті шешу, сонымен қатар кесіндіні қақ бөлу арқылы нөлдерін тауып, сол арқылы теңсіздіктің шешімін анықтау әдістері қарастырылады. Жоғарыда айтқандай трансцендентті теңсіздікті шешудің біріңғай жалпы әдісі жоқ, алайда теңсіздіктің құрамындағы трансцендентті функциялардың беріліуіне қарай тиімді әдісті өзіміз қарастыруымыз қажет. Әдетте мектеп бағдарламасындағы трансценденттік теңсіздіктердің құрамында бір типті трансценденттік функциялармен беріледі немесе әртүрлі екі трансцендентті функцияның көбейтіндісі түрінде кездеседі . Бірінші жағдайда, берілген теңсіздік трансцендентті функцияның негізгі қасиеттеріне сүйеніп шешілсе, екінші жағдайда, берілген теңсіздік мүмкін мәндер жиыны ескеріле отырып, интервалдар әдісімен шешіледі. Ал, құрамында әртүрлі бірнеше трансцендентті функциялардың айнымалысы болып келетін теңсіздіктер мектеп бағдарламасында қарастырылмайды. Бұл жағдайда, берілген теңсіздіктің шешімін туындының көмегімен немесе графиктік әдіспен анықтаймыз. Дәл осындай күрделі трансценденттік теңсіздікті шешуді оқытудың әдістемесін жасап, оны білім алушыларға тиімді тәсілмен ұсыну осы ғылыми жұмыстың өзектілігі болып табылады.

1 Трансценденттік теңсіздіктерді шешудің теориялық негіздері

1. 1 Бір айнымалысы бар теңсіздіктерді шешумен байланысты негізгі ұғымдар

Теңсіздікті шешу - емтиханда тестте ең көп кездесетін тапсырмалардың бірі. Мұндай теңсіздіктерді шешу үшін ең алдымен қарапайым теңсіздіктерді шешуді меңгеруі тиіс - алгебралық, көрсеткіштік, логарифмдік, тригонометриялық және т. с. с - және мектеп курсында қарастыратын функциялардың қасиеттерін білуі шарт. Сонымен қатар, әрине теңсіздіктердің қасиеттерін қолдана білуі керек.

Теңсіздікті шешу барысында да, теңдеуді шешкендегідей теңбе- теңдік ұғымы негізгі роль атқарады. Яғни кейінгі алынған теңсіздік алдыңғы теңсіздікке теңбе тең теңсіздік болатынына көз жеткізу қажет.

Сонымен қатар, төмендегі анықтамаларды ескерген жөн:

Теңсіздіктің мүмкін мәндер жиыны деп теңсіздіктің оң және сол жағының мәні болатындай белгісіздің барлық мәндер жиынын айтамыз.
Теңсіздікті шешімі деп теңсіздіктегі белгісіздің орнына апарып қойғанда теңсіздікті тура сандық теңсіздікке келтіретін белгісіздің барлық мәндерін айтамыз.
Теңсіздікті шешу - оның барлық шешімдерін табу немесе шешімі жоқ екенін дәлелдеу.
Екі теңсіздік теңбе тең деп аталады егер біріншісінің барлық шешімдері екіншісінің шешімдері болып табылса, немесе екіншісінің барлық шешімдері біріншісінің барлық шешімдері болып табылса.
Екі теңсіздік кейбір аралықта теңбе тең деп аталады, егер осы аралықта олардың бірдей шешімге ие болса.

Теңсіздікті шешуде жиі қолданатын теңсіздіктің бірнеше қасиеттерін топтастырып атап өтейік:

Теңсіздіктің екі жағына да берілген теңсіздіктің ММЖда анықталған бірдей функцияны қосуға болады. Егер f(x) > g(x) және h(x) - Берілген теңсіздіктің ММЖ анықталған функция, онда f(x) + h(x) > g(x) + h(x)
Егер теңсіздіктің екі жағын да оң функцияға немесе берілген теңсіздіктің ММЖ анықталған функцияға көбейтсек ( немесе оң санға), онда берілген теңсіздікпен эквивалент теңсіздікті аламыз:

егер f(x) > g(x) және h(x) > 0, онда f(x) h(x) > g(x) h(x)

Егер теңсіздіктің екі жағын да берілген теңсіздіктің ММЖ анықталған теріс функцияға көбейтсек( немесе теріс санға) онда теңсіздіктің таңбасы қарама қарсы жаққа ауысады және бұл теңсіздік берілген теңсіздікке эквивалент теңсіздік болып табылады:

егер f(x) > g(x) және h(x) < 0, онда f(x) h(x) < g(x) h(x)

Теңсіздік таңбасы бірдей теңсіздіктерді мүшелеп қосуға болады. Егер f(x) > g(x) және m(x) > h(x), онда f(x) + m(x) > g(x) + h(x)
Теңсіздік таңбасы қарама қарсы болған теңсіздіктерді мүшелеп азайтуға болады. Егер f(x) > g(x) және h(x) < m(x), онда f(x) - h(x) < g(x) - m(x) .
Екі жағы да оң теңсіздік таңбасы бірдей теңсіздіктерді мүшелеп көбейтуге болады. Егер f(x) > g(x) > 0 және m(x) > h(x) > 0, онда f(x) g(x) > m(x) h(x) .
Құрамында теріс емес функциядан тұратын теңсіздіктің екі жағын да бірдей теріс емес санға дәрежелеуге болады: Егер f(x) > g(x) > 0 және m > 0, онда (f(x) ) m> (g(x) ) m

Ескере кететін жайт, теңдеуді шешу барысында эквивалент теңдеуге әкелетін түрлендірулер теңсіздікті шешу барысында эквивалент теңсіздікке әкелмеуі мүмкін. Себебі, кейбір түрлендірулерден кейін белгісіздің мүмкін мәндер жиынына қатысты теңсіздіктер өзара бір мәндес бола алмайды.

Мысалы, егер $\log_{2}x < 1$ теңсіздігін шешу барысында, көпшілігі мынадай «шешім» беруі мүмкін « теңсіздікті мына түрде жазайық: $\log_{2}x < \log_{2}2$ логарифмдік функцияның қасиетінен бізге белгілі негізі 1 ден артық логарифмнің қай жағы үлкен болса, сол жағы артық . Сондықтан бұл теңсіздік х < 2 болғанда орындалады. Жауабы: х<2» . Мұндағы талдау мінсіз болып көрінгенімен қате жауап берілді, немесе бөгде шешімдер қосылып кетті деуге болады. Шындығында кез келген теріс сан екіден кіші, егер х теріс сан болатын болса, онда бастапқы теңсіздіктің мағынасы болмайды, себебі теріс санның логарифмі болмайды.

Неге бөгде шешімдер пайда болды? Себебі, жоғарыда теңсіздікті «шешу» барысында, біз мына теңсіздіктен $\log_{2}x < \log_{2}2$ мына теңсіздікке көштік х<2. Соңғы теңсіздік хтің екіден кіші барлық мәндерін қамтиды, ал бастапқы теңсіздікте ММЖ бойынша х тек оң сандарды қамтуы тиіс болатын. Демек, бірінші теңсіздіктен екінші теңсіздікке өту барысында ММЖ кеңейіп кетуі себепті, бөгде түбірлер пайда болды. Соңғы теңсіздіктен кейін дұрыс жауап алу үшін, бастапқы теңсіздіктің ММЖ енетін мәндерін алу керек еді: 0<х<2.

Теңсіздікті шешудің мына схемасы жиі қолданылады:

ең алдымен ММЖ анықтайды, сосын қажетті түрлендірулер жасалып теңсіздікті шешеді, соңында ММЖ енетін теңсіздіктің шешімдерін жауабы ретінде алады.

Сонымен қатар, теңсіздікті шешу барысында ММЖ кеңейтпейтін, бастапқы теңсіздікке эквивалент теңсіздікке түрлендіруге болатынын айтуға болады. Мысалы, lg(2-x) (x-3) <0, теңсіздігін (2-x) (x-3) <1 теңсіздігіне түрлендіруге болады, себебі бұл теңсіздіктің шешімі бастапқы теңсіздіктің ММЖ енеді, яғни 2<x<3 аралығында жатады.

Теңсіздіктің ММЖ зерттеу арқылы шешілетін, бірнеше қарапайым мысалдарды қарастырайық :

х>−1\sqrt{х} > - 1теңсіздігін шешейік. Теңсіздіктің сол жағында теріс емес өрнек болғандықтан, теңсіздік х тің ММЖ енетін барлық мәндері үшін орындалады, мұнда теңсіздіктің ММЖ х≥0\geq 0; және осы теңсіздіктің шешімі болып табылады.
lgx>0\sqrt{lgx} > 0\теңсіздігін шешейік. Бұл жағдайда да теңсіздіктің сол жағындағы өрнек теріс емес, сондықтан теңсіздік ММЖ енетін х тің кез келген мәні үшін орынды. Ал ММЖ ны мына шарт арқылы анықтаймызlgх≥0lgх \geq 0яғни бұдан х≥1\geq 1теңсіздігімен анықталады. Алайда х=1= 1болғанда теңсіздіктің сол жағы нөлге айналады, сондықтан белгісіздің бұл шешімі берілген теңсіздіктің шешімі бола алмайды. Берілген теңсіздіктің шешімі х>1 болады.
log⁡2−x(x−3) ≥−5\log_{2 - x}(\ x - 3) \geq - 5теңсіздігін шешейік. Бұл теңсіздіктің ММЖ мына шарттармен анықталады. х−3>0, 2−х>0, 2−х≠1х - 3 > 0, \ \ \ \ 2 - х > 0, \ \ \ 2 - х \neq 1. бірақ мұндах−3>0х - 3 > 0және2−х>02 - х > 0теңсіздіктерінің ортақ шешімдері жоқ. Демек, бұл теңсіздіктің ММЖ бос жиын, сондықтан берілген теңсіздіктің шешімі жоқ.
х+2+х−5=5−x\sqrt{х + 2} + \sqrt{х - 5} = \sqrt{5 - x}\теңсіздігін шешейік. ММЖ мына теңсіздіктермен анықталады. х+2≥0, х−5≥0, 5−х≥0х + 2 \geq 0, \ \ х - 5 \geq 0, \ \ \ 5 - х \geq 0. Бірақ бұл теңсіздіктер жүйесінің жалғыз шешімі бар, х=5= 5. Демек ММЖ бір ғана мәні бар х=5. = 5. Сондықтан теңсіздікке ешқандай түрлендіріулердің қажеті жоқ, тек х=5= 5мәні теңсіздікті қанағаттандыра ма жоқ па соны тексеру жеткілікті. Тексеру барысында х=5= 5теңсіздіктің шешімі екенін көрсетті.
sinх+2ctgx<−1\sqrt{{sinх}{+ 2ctgx}} < - 1теңсіздігін шешейік. Бұл теңсіздіктің сол жағы х тің кез келген мәнінде теріс емес болғандықтан, бұл теңсіздік х тің бір де бір мәні үшін орындалмайды яғни теңсіздіктің шешімі жоқ.

Келтірілген мысалдарда ММЖ ұғымы түрлі теңсіздіктерді шешуде қалай қолданылатыны көрсетілді. Алғашқы екі мысалда ММЖ ны таппастан, теңсізідіктің шешімін айта алмас едік, үшінші және төртінші теңсіздіктерде ең алдымен ММЖ табу арқылы теңсіздіктің шешімін жылдам тауып алдық. Керісінше, бесінші мысалда алдын ала ММЖ табу қиынырақ әрі мағынасыз болар еді, себебі теңсіздікті қанағаттандыратын х тің мәні болмайтыны теңсіздіктен көрініп тұр. Себебі, теріс емес өрнек -1 ден кіші бола алмайды.

Әрине, берілген барлық теңсіздікке қандай әдіс, қалай шешкен тиімді деген жалпы сұраққа жауап беру мүмкін емес. Әр теңсіздіктің берілгеніне қарай тиімді әдісті өзіміз таңдап аламыз.

Кейде, теңсіздікті шешу барысында, теңсіздікті түрлендіргенде нәтижесінде бастапқы теңсіздікке эквивалентті емес теңсіздікке алып келеді, ММЖ ның кеңеюіне байланысты, теңсіздіктің екі жағынан да бірдей функцияларды азайтқанда : f(x) - f(x) , теңсіздіктің екі жағын да ортақ көбейкішке қысқартқанда f (x) g(x) > f(x) h(x) ортақ оң f(x) функциясына қысқартқанда т. с. с. Осындай түрлендіруден соң шыққан шешім бөгде шешім болып қалуы мүмкін. Сондықтан, мұндай жағдайда жауабын жазарда бөгде шешімдерді алып тастап жазу керек.

1. 2 Теңсіздікті шешу тәсілдері

Теңсіздікті шешудің бірнеше тәсілдері бар, атап айтсақ, анықтама бойынша шешу, берілген теңсіздік құрамындағы функцияның қасиетіне қарай түрлендірулер арқылы шешу, жаңа айнымалы енгізу арқылы шешу, аралықтар әдісі бойынша шешу және графиктік тәсілмен шешу әдісі.

Әдетте орта мектеп курсында логарифмдік, көрсеткіштік, тригонометриялық, кері тригонометриялық теңсіздіктерді шешудің бірнеше әдістері қарастырылады. Атап айтсам, потенциялдау, көбейткішке жіктеу, жаңа айнымалы енгізу, интервалдар әдісімен шешу әдістері, алайда бір теңсіздікте әр түрлі трансцендентті функция кездессе немесе трансцендентті функциямен қатар алгебралық функция қатар кездессе, онда екі жағдайды орын алуы мүмкін:1) егер теңсіздік құрамындағы берілген өрнек көбейткішке жіктелсе, онда оларды көбейткішке жіктеп интервалдар әдісін қолданып шешеміз . 2) егер теңссіздік құрамындағы берілген өрнек көбейткішке жіктелмесе онда оларды графиктік әдіспен немесе туындының көмегімен монотондылыққа зерттеп қана шешімін көрсете аламыз.

Ал енді осы аталған әдістердің әрқайсысына тоқталайық.

Жаңа айнымалы енгізу әдісі

$1. \left( \log_{x}2 \right) \left( \log_{2x}2 \right) \left( \log_{2}4x \right) > 1$ теңсіздігін қарастырайық. Логарифмнің негізгі тепе теңдігін қолданып логарифмдерді 2 негізіндегі логарифмге келтіреміз, теңсіздік мына түрге келеді: $\frac{\log_{2}4x}{\log_{2}x*\log_{2}2x} > 1\, \ \ \log_{2}x = y\ \ деп\ жаңа\ айнымалыы\ ауыстырсақ\ \ \$

$\frac{2 + y}{y(1 + y) } > 1 \rightarrow \frac{y^{2} - 2}{y(y + 1) } < 0\$ берілген теңсіздікті интервалдар әдісімен шешетін болсақ: $- \sqrt{2} < y < - 1, \ \ \ 0 < y < \sqrt{2} \rightarrow - \sqrt{2} < \log_{2}x < - 1, \ \ \ 0 < \log_{2}x < \sqrt{2}$

Демек теңсіздіктің шешімі $2^{- \sqrt{2}} < x < \frac{1}{2}\ \$ және $1 < x < 2^{\sqrt{2}}$ .

$2. \ \ \ \ \ x^{\log_{2}x - 2} > \frac{x}{4}\$ теңсіздігін шешейік.

Берілген теңсіздіктің екі жағын да 2 негізде логарифмдесек берілген теңсіздік мына теңсіздікпен мәндес болады: $\log_{2}x^{\log_{2}x - 2} > \log_{2}\frac{x}{4} \rightarrow {(log}_{2}x - 2) \log_{2}x > \log_{2}x - 2, \ \ \ \ \ \ \log_{2}^{2}x - 2\log_{2}x - \log_{2}x + 2 > 0$

$\log_{2}^{2}x - 3\log_{2}x + 2 > 0$ , $y = \log_{2}x, \ \ y^{2} - 3y + 2 > 0 \rightarrow \left\lbrack \begin{array}{r} y < 1 \\ y > 2 \end{array} \rightarrow \right. \ \left\lbrack \begin{array}{r} \log_{2}x < 1 \\ \log_{2}x > 2 \end{array} \right. \ \rightarrow \left\lbrack \begin{array}{r} x < 2 \\ x > 4 \end{array} \rightarrow \left\{ \begin{array}{r} x > 0 \\ \left\lbrack \begin{array}{r} x < 2 \\ x > 4 \end{array} \right. \ \end{array} \rightarrow x \in (0; 2) \cup (2; 4) \right. \ \right. \$ Жауабы: $(0; 2) \cup (2; 4)$

Потенцирлеу әдісі

Бұл әдіс бойынша теңсіздікті шешкенде теңсіздік құрамындағы функцияның өспелі немесе кемімелі болатынына байланысты потенцирлегеннен соң теңсіздік таңбасының ауыспайтынын немесе ауысатынын ескеру қажет.

1. $4\log_{16}cos2x + 2\log_{4}sinx + \log_{2}cosx + 3 < 0, \ \ \ (0 < x < \frac{\pi}{4})$ теңсіздігін шешейік.

Ең алдымен логарифмнің негізгі тепе теңдіктерін қолдансақ берілген теңсіздік мына түрге келеді: $\log_{2}cos2xsinxcosx*8 < 0$

$\log_{2}2sin4x < 0 \rightarrow \ \log_{2}2sin4x < \log_{2}1\$ логарифмнің негізі 1 ден артық болғандықтан, теңсіздікті потенцирлесек $2sin4x < 1 \rightarrow sin4x < \frac{1}{2}\ \ \ \ \ \ \ \ \ \ - \frac{7\pi}{6} + 2\pi n < 4x < \frac{\pi}{6} + 2\pi n, \rightarrow - \frac{7\pi}{24} + \frac{\pi}{2}n < x < \frac{\pi}{24} + \frac{\pi}{2}n_{}, n \in Z$

$\left\{ \begin{array}{r} - \frac{7\pi}{24} + \frac{\pi}{2}n < x < \frac{\pi}{24} + \frac{\pi}{2}n, n \in Z \\ 0 < x < \frac{\pi}{4} \end{array} \rightarrow 0 < x < \frac{\pi}{24} \right. \$ жауабы (0; $\ \frac{\pi}{24}$ )

2. $arcsinx + \arccos(x - 1) < \pi$ теңсіздігін шешейік.

Берілген теңсіздіктің құрамында $- \frac{\pi}{2} < arcsinx < \frac{\pi}{2}\, \ \ \ \ \ және\ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 < \arccos(x - 1) < \pi\,$ болғандықтан берілген теңсіздікті (0; $\ \pi)$ аралығында шешсек берілген теңсіздік төмендегі теңсіздікпен мәндес болады:

$\sin(arcsinx) < \sin\left( \pi - \arccos(x - 1) \right)$ , $\sin(\pi - \alpha) = sin\alpha$ екенін ескеріп, $\sin(arcsinx) < \sin{\left( \arccos(x - 1) \right) \rightarrow}\ \ \ \ \ \ \ x < \sqrt{1 - (x - 1) ^{2}}$

$x < \sqrt{2x - x^{2}}\ \$ теңсіздігі төмендегі жиынтықпен мәндес: $\left\lbrack \begin{array}{r} \left\{ \begin{array}{r} x > 0 \\ x^{2} < 2x - x^{2} \end{array} \right. \ \\ \left\{ \begin{array}{r} x \leq 0 \\ 2x - x^{2} \geq 0 \end{array} \right. \ \end{array} \right. \ \rightarrow \left\lbrack \begin{array}{r} \left\{ \begin{array}{r} x > 0 \\ 2x^{2} - 2x < 0 \end{array} \right. \ \\ \left\{ \begin{array}{r} x \leq 0 \\ x(2 - x) \geq 0 \end{array} \right. \ \end{array} \rightarrow \left\lbrack \begin{array}{r} x \in (0; 1) \\ x \in ( - \infty; 0\rbrack \end{array} \rightarrow \right. \ \right. \ x \in ( - \infty; 1)$