Графтардың байланысу критериі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Кіріспе

Графтар теориясы (ағылш. graph theory) -- түйіндері нүктелер жиыны, ал түйіндердің жалғасуы (қабырға деп аталатын) парлы екі нүкте болып келетін тор түрінде бейнеленеді. Егер түйіндердің жалғасу реті айтарлықтай маңызды болса -- бағытталған граф, әйтпесе бағытталмаған граф болады. Графтар информатикада кеңінен қолданылады, айталық, алгоритмдер схемасы немесе программалар бағытталған графтарға жатады.
Бағдарланбaғaн граф (Неориентированный граф) -- төбелерді қосатын доғаларының бағыты болмайтын граф.
Бағдарланған граф (Ориентированный граф; directed graph) - әр түрлі төбелер жұбын жалғастыратын қабырғалармен бірге түйіндердің (немесе төбелердің) құр ақырғы жиыны. Әдетте, граф көрнекті формада ұсынылады, сонымен бірге төбелері нүктелермен немесе кейде ұқсастыру мақсатымен ентаңбаланған басқа мүсіндермен, ал қабырғалары сәйкес нүктелерді жалғастыратын сызықтармен кескінделеді. Егер әрбір қабырғаға бағыт көрсетілсе, онда мұндай граф бағдарланған граф деп аталады. Бұл жағдайда қабырға әр түрлі төбелердің реттелген жұбының жиынын үйымдастырады және оларды көбінесе доға деп атайды. Бағдарланған граф көрнекті түрде ұсынылған кезде әрбір доға жебелікпен жабдықталады.
Зерттеу жұмысының нысаны - мектепте Алгебраны оқыту процесі.
Зерттеу жұмысының пәні - мектепте Алгебраны оқыту процесінде әдістерді жан-жақты тиімді пайдалану - оқыту сапасын, оқушылардың пәнді оқуға ынтасын арттырады.
Диплом жұмысымның мақсаты - графтар теориясы таңдау курсын орта мектеп оқушыларына енгізу бағдарламасын практикалық тұрғыда зерттеу және бақылау. Бұл курс жоғары сынып оқушыларына дербес компьютерді пайдалана отырып жүргізуге арналған. Ол оқу процесінің есептерін білімді, іскерлікті және дағдыны қалыптастыру үшін құруға болмайды деген ұстанымы бар қазіргі заманға сәйкес дидактиканың қойған есептерін шығаруға бағытталған. Қазіргі таңда білім беру ісі тек теориялық және практикалық білімді меңгеруге ғана емес, сонымен жалпыбілімдік іскерлік пен дағдыларды игеруге жұмыс істеп келеді. Жоғары сынып оқушыларын жаңа графтар теориясы пәнімен таныстыру оқу процесінің талабы болып табылады.
Бұл мақсатқа жету үшін алдымызға мынадай міндеттер қойып отырмыз:
Графтардың тақырыбының мектеп бағдарламасындағы алатын орнын айқындау;
Графтардың түрлері және қасиеттерімен таныстыру;
Жұмысты орындау барысында мынадай әдістер қолданылды:
педагогикалық, әдістемелік және математикалық әдебиеттерді талдау және сараптау;
Қорғауға ұсынылатын негізгі қағидалар:
Торлар мен графтартың түрлері және олардың қасиеттерімен таныстыру;

1.1 Графтар теориясының қалыптасу тарихы

Графтар теориясы - бұл математика бөлімшелердің бірі, объектілерін зерттеу геометриялық әдісі болып табылады, оның негізгі ерекшелігі болып табылады. Ол негізін қалаушы болып саналады атақты математик Эйлер.
19 ғасырдың аяғына дейін графтар теориясын қолдану, қызықты мәселелерді шешуге азайды және айтарлықтай қоғам назарын тартылды. графтар теориясы тәуелсіз математикалық пән ретінде қалыптасты кезде 20-шы ғасырдың бастап, ол кеңінен осындай кибернетика, физика, логистика, бағдарламалау, биология, электроника, көлік және байланыс жүйелері сияқты салаларда қолданылады.
Негізгі түсініктер графтар теориясы
The базасы болып табылады бағандары. терминология бағанға бірдей желіге сияқты затты табуға болады. Өткен - балл, яғни, биіктерге және сегменттерінің бос емес саны, ұпай берілген санына сәйкес екі ұшы оның шығыңқылар, яғни. Graph теориясы емес, Invest белгілі бір нүктесі жылы The құндылықтар жиектері мен шыңдары. Мысалы, бірінші қалалық және оларды қосатын жолдар, - бұл графиктің жоғарғы болып табылады, ал екінші - қабырғаның. Үлкен маңызы доғалар теориясы беріледі. шеттері бағыты бар болса бағытталған Шеттері бағандары, ол digraph деп аталады, егер ол, доға деп аталады.
Мынадай ұғымдар ретінде теориясы терминология:
Подграф график, барлық шеттері мен шыңдары шыңы және жиектер бірі болып табылады.
Қосылған Graph - екі түрлі шыңдары оларды байланыстыратын тізбек бар бар бір.
Сараланған қосылған Graph - салмақтық функциясын орнатуға бірі.
Tree - циклі жоқ графигін байланысты.
Қаңқасы - ағаш подграф.
ұшақ анықталды белгілеу график суретте пайдаланылады: Таңдалған бұрыштық нүкте бастауыш бетіне сәйкес келеді және Edge шыңы арасындағы болса, тиісті ұпай сегментін біріктіріледі. Graph бағытталған болса, осы сегменттер көрсеткі ауыстырылады.
Бір кестеде астам бір графикалық ұсыну берілуі мүмкін, өйткені Бірақ бұл, дерексіз құрылымы бар, яғни онымен графикте, имиджін салыстыру қажет емес. ұшақта сызу биіктерге жұп жиектерін біріктірді, және ол емес болып табылатын көру үшін беріледі.
Графиктер шығару теориясының мәселелері кейбір арасында:
The міндет The қысқа тұйықталу (аппараттық ауыстыру, орналастыру, жедел жәрдем және телефон станциялары).
Ең ағыны проблема (динамикалық желіге тапсырыс қозғалысы, жұмыс тарату, сыйымдылығы ұйымдастыру).
жабындарды және пакеттер (тұру диспетчерлік орталықтар) проблемасы.
(Электронды компьютерлерде жад орналастыру) бағандарда бояғыш.
Байланыс желілері және графиктер (байланыс желісін, байланыс желілерін талдау жасау).
Қазіргі уақытта ол графтар теориясының етпестен міндеттерді көпшілігін бағдарламалау мүмкін емес. Бұл жасайды жеңіл және оңай жұмыс бар компьютерлер.
Бағдарлама проблемаларды шешу үшін құрылымдар мен әмбебап түрлі әдістерді пайдаланады, және олардың бірі Графтар теориясы болып табылады. Оның маңыздылығы бағалау қиын болады. бағдарламалау бойынша графтар теориясы, ақпарат алу үшін іздеу жеңілдету үшін бағдарламалық қамтамасыз ету оңтайландыру, түрлендіру және деректерді тарату мүмкіндік береді. алгоритмдер теориясының арқасында, бағдарламаның соңғы нұсқасын математикалық айқындылығы дәрежесін азайту жоқ, алгоритм, өзгертілуіне жүзеге асыруға, белгілі бір мақсатқа пайдалану үшін қолдану және бағалау мүмкіндігі бар.
бақылау жүйесінің немесе моделін маңызды мүліктік жиынтығы бинарлы қатынастарды іс-әрекеттер мен деректер бірлік жиынтығымен. Бұл құрылымдар The ғана бөлігі The бағдарламасы және The ақпарат болып табылады қайта оларды. Сондықтан, графиктер бағдарламашы үшін жобалау негізделген.

1.2 Графтың негізгі терминдері мен қажетті дәлелдеулер.

G графы деп Х төбелер жиынынан және олардың кейбіреулерін қосатын сызықтардан тұратын жиынды айтады. Доға деп бағытталған қабырғаны ұғамыз.Сонымен, G графы екі элементтен тұрады: қабырғадан,төбеден.Оның белгіленуі: G(Х,Е), мұндағы Х-төбелер жиыны,Е-қабырғалар жиыны.
Егер Е жиынында барлық жұптар реттелген (қабырғалары бағытталған) болса,онда бұл-орграф.Граф төбелері қабырғамен қосылмауы (іргелес емес), төбелері қабырғамен қосылуы(іргелес) тіпті көптеген қабырғалармен (еселі) қосылған болуы мүмкін.Сонымен қатар төбенің өзі-өзімен қосылуы мүмкін(жіп түрінде).
Егер х төбесін басқа бір төбемен қосатын болса,онда х төбесі Еx қабырғасына қарсы жатады.
1.3 Ішкі граф, толық граф, ноль-граф, қосымша граф.
G(Х,Е)графының G(Х1,Е1) ішкі графы деп Х жиынына тиісті көптеген Х1 төбеден, Е1 дің әр қабырғасы тек Х1ге ғана қарсы болатындай көптеген Е1 қабырғадан тұрады,яғни, ішкі графтың құрамында шығатын графтың кейбір төбелері және екі ұшы да осы ішкі графқа кіретін кейбір қабырғалары бар.
Егер ішкі графтың төбелері графтың өзінің төбелерімен сәйкес келсе, онда бұл негізгі ішкі граф деп аталады.
V жиынының төбелерінен туындаған ішкі граф деп V жиынынның төбелерінен және тек екі ұшы ішкі графта жататын қабырғалардан құралған ішкі графты атаймыз.
Осттық ішкі граф деп төбелерінің жиыны графтың төбелерінің жиынымен сәйкес келетін ішкі графты атаймыз.
а және b төбелері іргелес деп аталады егер аларды өосатын Е қабырғасы

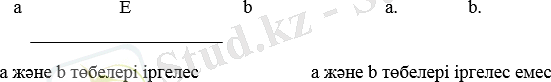
Е1 және Е2 қабырғалары іргелес егер бір уақытта Е1 және Е2 қабырғаларына инцидентті а төбесі табылса.

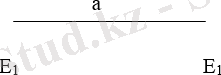
Графтың төбелерінің саны немесе 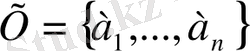жиынының қуаты реттелген граф деп аталады. n - ші ретті G графы Gn түрінде белгіленеді.
Кn - n ретті толық граф деп кез келген екі төбесі іргелес болатын n төбелі графты атаймыз.
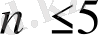болатын толық графтар төменде көрсетілген:

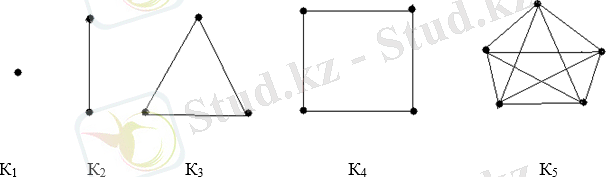
Кn толық графтың қабырғасына тұратын Vn жиыны n- ретті Gn графтардың жиынының арасындағы қабырғаларының саны максимум болатын жиын, Кn анықтамасы бойынша, оның кез келген екі қабырғасы іргелес болғандықтан оның қуаты Vn=Cn*Cn=n(n-1)2.Реті n- ге тең нольграф(бос граф), оның қабырғалары жоқ.Ол n аластатылған төбелерден тұрады,және графтар алгебрасында нольдің ролін атқарады.G(Х,Е) графының толықтауышы деп төбелерінің жиыны Х - тің төбелер жиынымен беттеседін және оның кез келген екі төбесі іргелес болады,сонда ,және тек сонда ,егер олар С1 графында іргелес болмаса ,яғни G1 =G (Х,Е), мұнда Е қабырғалар жиыны Е - нің V - ға дейінгі толықтауышы. V - Кn толық графының қабырғалар жиыны: Е1 = V Е.Бұдан G және оның толықтауышының G1-дің қосындысы толық графқа тең.

1.4 Графтың төбелерінің дәрежесі, және оның қабырғаларының саны.

G n графының а төбесінің дәрежесі деп,оған инцидентті қабырғалар санын айтамыз.0=т=n-1 екені анық.Ноль дәрежелі графтың төбелері оқшауланған, ал бірінші дәрежелі граф аяқтаушы ,ілінген немесе бет (висячей.или листом) деп аталады.
G n графының төбелерінің {t(a1),...,t(an)} дәрежелерінің жиыны - оның маңызды мінездемесі болып табылады және ол арқылы граф қабырғаларының N саны анықталады.
Теорема 1 .N=N(Gn)=(t(ai)+...+t(an))2, яғни екі еселенген қабырғалар саны оның төбелерінің қосындысына тең.
Теореманың тұжырымының дұрыстығы оның дәрежелерінің қосындысында оның әр төбесі екі рет ескеріледі.
Салдар 1. Шекті графта тақ дәрежелі төбелер саны - жұп.
Егер графтың кез-келген төбесінің дәрежесі r-ге тең болса, онда бұл r граф r-дәрежелі біртекті граф деп аталады.
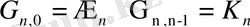
Салдар 2. r дәрежелі тұрақты Gn,r графының қабырғалар саны N(G)=n*r2.Себебі 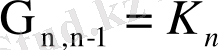n ретті тұрақты n-1 дәрежелі граф,онда оның қабырғаларының саны Vn=n(n-1)2=C2n, мұндағы Cmn n элементтен m-нен алынған терулер Cmn=n!(m!(n-m)!) саны.Үшінші дәрежелі тұрақты граф кубтық граф болады.Бұл теоремадан r-дің тақ болу мүмкіндігі тек n - нің жұп болу жағдайында ғана бар екенін көреміз.
Теорема2. Кез - келген Gп(п=2) графында бірдей дәрежелі кем дегенде екі төбе
табылады:t(a)=t(b)
Салдар 3. Егер графта дәрежесі бірдей тек екі ғана төбе табылса,онда нақты түрде ноль дәрежелелі бір төбе немесе n - 1 дәрежелі бір төбе табылады.
1.5 Графтың изоморфтылығы.

Графтың қасиеттері оның бейнесіне тәуелді емес( қабырғалары түзу ме әлде қисық па, олардың төбелерінің ара қашықтығына байланысты емес т.с.с ) . Бұл инварианттың нақты сипаттамасы екі граф
тың изоморфизмі ұғымында келтірілген.
G1(Х1,Е1) және G2(Х2,Е2) екі графы изоморфты, егер олардың төбелерінің жиыны арасында өзара бірмәндік сәйкестік бар болса, яғни бір графтың кез келген сыбайлас төбелер жұбына екінші графтың кез келген сыбайлас төбелер жұбы сәйкес келсе.
Теорема-3 .Изоморфты сәйкестікте сәйкестендірілген төбелердің дәрежелері бірдей.
G1 және G2 изоморфты, а төбесі G1-ге тиісті болсын. G2-дегі а1-ді а-мен сәйкестендірейік. а және b сыбайлас болсын. Онда G1-дің b төбес оның әртүрлі(Е0, Е1,..., Ек ) қабырғаларының шекті тізбегін айтады іне G2-нің (a`, b`) қабырғасы сәйкес келеді.
Салдар-4. Изоморфты графтардың төбелерінің дәрежелері тең болады.
Мысалы.Тетраэдр графы К4 изоморфты:

Ескерту: Теорема графтың изоморфтылығында ғана қолданылады, қ ежелден шешімі табылмай келе жатқан мәселені шешпейді, яғни берілген графтың изоморфтылығын анықтамайды.

Мысалы:
Үшбұрышты призма графы және К3,3 графының реті алты, бұл үш диаметрлі алтыбұрыштөбелерінің дәрежесі бірдей(3,3,3,3,3,3).Бірақ бұл графтар өзара изоморфты емес және бір-біріне ұқсамайды, себебі призма графы планарлы, ал К3,3 - планарлы емес,яғни оны жазықтықта төбелерін қосатын қабырғаларды қиылыспайтындай етіп көрсетуге болады.(Бірақ бұл г
рафтан бір қабырғаны алып тастасақ бұл граф планарлы.)

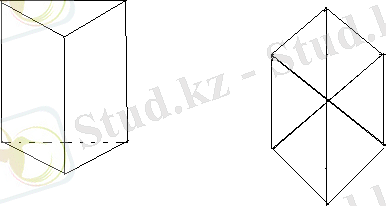
3- призма Граф К3,3
1.6 Граф жолдары және байланысу ұғымы.
Граф жолдары (маршруты)деп - Еі-1 және Еі көршілес қабырғалары бір төбеде қиылысатындай, оның әртүрлі(Е0, Е1,..., Ек ) қабырғаларының шекті тізбегін айтады .Сонымен , егер, (Е0, Е1,..., Ек )- жол болса, онда Е0= (а0,а1) Е1= (а1,а2), ... Еm =(аm, аm+1)олар жолдың ішкі төбелері деп аталады.Барлық төбелері ішкі болатын жол - тұйықталған жол деп аталады. Барлық қабырғалары қос-қостан алғанда әртүрлі болатын жолды шынжыр деп атаймыз. Тұйықталған шынжыр - цикл деп аталады. Егер шынжырдың немесе циклдің барлық төбесі бір рет кездесетін болса, онда шынжыр немесе цикл - жай деп аталады.
Мысалы:
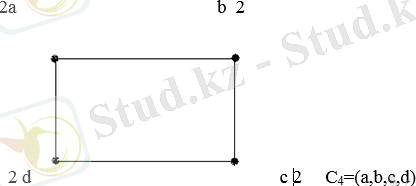
G5 - диагональдарының қиылысу нүктесін қосқандағы ABCD тік төртбұрышы:

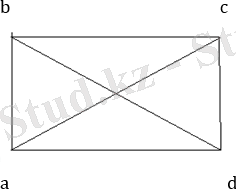
S=( ab, bc, ce, ed, dc) a төбесімен басталып b төбесімен аяқталатын жол. Бұл жол жай жол емес, себебі c төбесі екі рет кездеседі.
S1=(ab, bе, ec, cd, de,еа)- цикл, бірақ жай емес.
S2=(ab, bе, ec, cd, dа)- жай цикл, S3=(ab, bе, ec, cd) - жай шынжыр.
Байланысқан шынжыр деп - оның кез келген a және b төбелерін қосатынS(а,в) жол табылатын шынжырды айтамыз. Бұл жағдайда a және b төбелері байланысқан деп аталады, себебі қабырғалар арқылы a төбесінен b төбесіне өтуге болады. а мен байланысқан барлық төбелерден туындаған GаG ішкі графты а төбесінің Gа байланысуының компонентасы деп атаймыз.
Тұжырым 1 Егер а Gа, онда Gа Gb яғни, а төбесінің байланысуының компонентасы бір уақытта оған кіретін төбелердің әрұйсысының байланысу компонентасы болып табалады.
Теорема 4. Кез-келген қарапайым графты қиылыспайтын байланыстардың компонентасына бөліктеуге болады. G=G1+...+Gq (q=1)
Салдар 5. Егер q=1,онда G графы толығымен бір байланысу компонентасы болып табылады,яғни G байланысқан граф.Егер 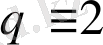онда G=G1+ G2 екі компоненттіл байланыспаған граф .
(a,b) қабырғасы G графындағы кқпір деп аталады,егер одан a және b төбелерін алып тастағанда байланыспаған граф шықса,яғни, G ішкі графы байланбаған G= G{ a,b }
Көпірдің анықталған белгілерін келтірейік:
(a,b) қабырғасы көпір болады сонда,тек сонда егер a,b төбелерін қосатын тек бір ғана жол табылса.
(a,b) қабырғасы қабырғасы көпір,егер кез-келген S(c,d) жолы а және b төбелерін қамтитын c және d төбелері табылса.
(a,b) қабырғасы қабырғасы көпір,сода,тек сонда егер ол ешбір циклға кірмесе.
1.7 Графтардың байланысу критериі.
Төменде байланысудың екі критериі берілген: бірі граф қабырғаларының саны N арқылы,екіншісі оның төбелерінің жиыны арқылы.
Теорема 5.
Граф қабырғаларының саны N: N Ø С 2n-1 =((n-1)(n-2))2 болса, онда бұл граф Gn - байланысқан.
Салдар 6.Байланыспаған Gn= Кn-1 {а n} графтың қабырғаларының максимал саны С 2n-1 - ке тең, ал байланысқан графта - С 2n және ол Кnтолық графта орындалады.
Теорема 6.
Егер де кез келкен a және b төбелер жұбы үшін t(a)+ t(b)= n орындалса, онда бұл Gn граф - байланысқан.
Салдар 7. Егер кез - келген Gn графының төбелерінің дәрежесі n2 - ден кем болмаса, онда бұл граф байланысқан.Графтың t(a)+ t(b)= n шартын қанағаттандыратын кез-келген төбелерінің жұбы үшін байланысқан графтың N қабырғаларының санын бағалайық.Төбелер саны n2-ге тең болғандықтан әрбір жұбы үшін t(a)+ t(b)=0 онда қабырғалар саны N 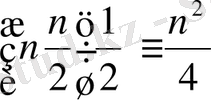-ден кем емес ,яғни
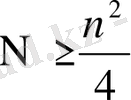
Ескерту. 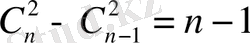сондықтан 1- критериге (теорема 5) қабырғаларының саны квадраттар болатын грфтар класы жатады.
,,...,
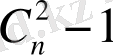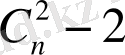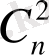
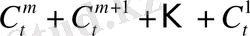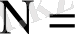
Олардың саны мұнда 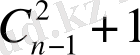және 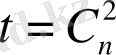2-критеиге де қабырғаларының саны квадраттар болатын графтар сай келеді
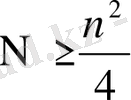
Бұдан қабырғаларының саны 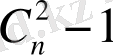-ден кем ,дербес жағдайда қабырғаларының саны сызықтық болатын байланысқан графтардың бар болуы туралы сұрақ туындайды.Сонымен қатар n-ретті байланысқан графтардың қабырғаларының минимал саны қандай болуы керек деген сұрақ туындайды.
Теорема 7. Gn байланысқан графының қабырғаларының минималды саны n-1 - ге тең және оған ,мысалы ,n төбелерді қосатын жай циклде жетеді.
Циклсіз байланысқан граф ағаш,ал циклсіз жай граф орман деп аталады.Тn ағашының n төбесінде n-1 қабырғасы бар, себебі оған енді кем дегенде бір төбе қоссақ, ол цикл құрайды. Бұдан k ағаштан тұратын Fn орманы n төбесінде N(Fn)=n-k төбесі болады. Егер k=1 болса, онда орман бір ағаштан тұрады. Қабырғалардың саны n-1.
Теорема 8.Графтың ағаш бола алады сонда,және тек қана сонда,егер кез-келген екі төбесі бір ғана шынжырмен байланысқан болса.
Gn графының a және b төбелерінің арақашықтығы d(a,b) деп сол екі төбені қосатын ең қысқа арақашықтықты айтамыз.
a,bEuro Gn үшін d(a,b)= n-1 екені түсінікті.
Х төбесінен графтың басқа төбелеріне дейінгі ең ұзын арақашықтықты - эксцентриситет e(x) деп атаймыз.D(a)- графтың диаметрі деп эксцентриситеттің ең үлкенін айтамыз
R(a)-графтың радиусы деп ең кіші эксцентритетті айтамыз.
Ағаштың e(x)=R(a) болатын төбесі оның түбірі деп аталады.
Теорема 9.Әрбір ағаштың бір ғана түбірі немесе екі сыбайлас түбірі болады.

Салдар 8. Диаметрі жұп болатын теректің тек бір тамыры,ал диаметрі тақ

теректе екі сыбайлас тамыр боады.
Егер графтың к - дан кем емес төбелерін алып тастағанда байланысу бұзылса, онда бұл граф - к - байланысқан граф деп аталады.Егер к екіден артық болса, онда бұл граф көпбайланысқан деп аталады.

Графтардың айналымы

Граф-эйлер графтары деп аталады, егер онда оның барлық қабырғалары бір рет қатысатын (қарапайым қабырғалы цикл) цикл бар болса.
Теорема-10.
Граф байланысқан және барлық төбелерінің дәрежесі жұп болған жағдайда ғана эйлер графы болады.
Салдар-9.
Графтың тақ дәрежелі тура екі төбесі болса ғана бұл байланысқан граф эйлер шынжырын(циклін емес) құрай алады, сонымен қатар оның толықтауышы да эйлер шынжырын құрайды.
Графтың барлық төбелері арқылы өтетін жай цикл табылса онда бұл граф гамильтон графы деп аталады(гамильтон циклі). Графта гамильтон графының
табылатындығын жоққа шығаратын критери Эйлер критериі сияқты әлі табылған жоқ. Сондықтан бұл жерде жеткіліктілік критериімен шектелеміз.
Теорема-11
Кез келген графтың a,b төбелері үшін олардың дәрежелерінің қосындысы n-нен кем емес болса, онда граф- гамильтон графы. n: t(а)+ t(b ) =. n
Салдар-10. [Dirac,1941]
Егер кез келген а төбесінің дәрежесі t(а) n 2 - ден кем болмаса, онда граф гамильтон графы . t(а) = n 2.
Салдар-11.
Қабырғалар саны n 24 - ден кем емес граф- гамильтон графы деп аталады. N(G(n,r))= nr2= n 24 осыдан r= n 2.

Мысалы:Тақ ретті толық Кn графы- эйлер және гамильтон графы және (n-1)2 гамильтондық циклдерінің бірігуін білдіреді.Сонда, К5 - бесбұрыштың және бесжұлдыздың қосындысы.

Теорема 12.[Понтрягин Л.С,1927ж] Граф-планарлы, егер К5 және К3,3-ке гомеоморфты ішкі графтары жоқ болса.
Салдар 12. Граф-планарлы, егер онда К5 немесе К3,3-ке изоморфты ішкі графтары жоқ болса.
Теорема 13.[Вагнер,1937 ж] Графты К5 немесе К3,3 ішкі графтарына қарай созуға болатын болса ғана ол планарлы граф деп аталады.
Пентагон мен пентаграмманың қосындысы болып табылатын Петерсеннің оныншы тізбектегі Gp кубтық графы жоспарланбаған, себебі ол айқын жолмен К5 ішкі графына қарай созылады.

Бұл ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.