GeoGebra бағдарламасын қолдана отырып салу есептерін шешу әдістері


Қазақстан Республикасы Білім және ғылым министрлігі
Қорқыт Ата атындағы Қызылорда университеті
Беген Д.
GeoGebra бағдарламасы арқылы салу есептерін шешу әдістері
ДИПЛОМДЫҚ ЖҰМЫС
мамандығы: 050109 - «Математика»
Қызылорда, 2021
Қазақстан Республикасы Білім және ғылым министрлігі
Қорқыт атындағы Қызылорда университеті
«Физика және математика» кафедрасы
«Қорғауға жіберілді»
Кафедра меңгерушісі
«___» 2021 ж.
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: «GeoGebra бағдарламасы арқылы салу есептерін шешу әдістері»
мамандығы: 050109 - «Математика»
Орындаған: Беген Д,
М-17-1 п/я оқу тобының студенті
Ғылыми жетекшісі: Г. А. Кудебаева, п. ғ. м., аға оқытушы
Қызылорда, 2021
Мазмұны
Кіріспе . . .
1. Салу есептерін шешу әдістемесі
1. 1 Салу есептері . . .
1. 2 Салу есептерін шешу әдістері . . .
1. 3 Геометрия оқулықтарындағы «Салу есептері» тақырыбындағы оқу материалдарын талдау
2. «GeoGebra» бағдарламасында салу есептерін шешу әдістері . . .
Қорытынды . . .
Пайдаланылған әдебиеттер тізімі . . .
Кіріспе
Салу есептері оқушылардың геометрияға деген қызығушылығын қалыптастырудың маңызды құралы болып табылады.
Геометриялық салуларға б. э. д. VI - V ғасырларда ежелгi грек математиктерi ерекше назар аударған. Пифагор (б. э. д. VI ғ) және оның шәкiрттерi, Гиппократ (б. э. д. V ғ), Евклид, Архимед, Аполлоний (б. э. д. III ғ), ежелгi отырарлық Әл-Фараби (870 - 950 ж. ж. ) геометрияның осы саласына өз үлестерiн қосып, оны дамытты.
Бүгінгі таңда геометрияны конструктивті тапсырмаларсыз елестету мүмкін емес. Конструктив тапсырмалары фигураларды құру дағдыларын дамытып, сызбаны оқу және түсіну қабілетін қалыптастыруға, оның бөліктері арасында байланыс орнатуға ықпал ететін болғандықтан, бұл жүйенің жетіспеушілігі оқушының кеңістіктік және логикалық ойлауының нашар дамуына, оның графикалық мәдениетінің төмендеуіне әкеледі.
Оқытуда компьютерлік технологияларды қолдану - білім беру процесін дамытудың ең тұрақты бағыттарының бірі болып табылады. Салу есептерін шешуде "GeoGebra" бағдарламасын пайдалану оқушылардың жеке дайындығын жетілдіріп қана қоймай, оқуға деген қызығушылығын арттырады.
Дипломдық жұмыстың объектісі - негізгі мектеп курсында геометрияны оқыту процесі.
Зерттеу пәні - орта мектеп оқушыларына «GeoGebra» бағдарламасын қолдана отырып, конструктивті есептер шығаруды үйрету.
Мақсаты: салу есептерін шығарған кезде «GeoGebra» бағдарламасының функционалын зерттеу.
- Салу есептерiн шешу әдiстерi
1. 1 Салу есептері
Конструктивті салу тапсырмаларында берілген шарттарға сәйкес геометриялық нысанды салу қажет.
Егер бұл шарттар қажетті фигураны анықтау үшін қажет және жеткілікті болса, тапсырма нақты деп аталады. Оның бір немесе бірнеше шешімдері болуы мүмкін.
Егер фигураны анықтау үшін жеткіліксіз шарттар берілсе, тапсырма анықталмаған болып табылады.
Кез-келген салу құралдарын қолдана отырып есептерді шешкен кезде олар конструктивті геометрияның келесі аксиомалары қолданылады:
- Егер кез-келген фигура "берілген" болса, ол салынған деп саналады.
- Егер екі (немесе одан да көп) фигура салынған болса, онда бұл фигуралардың бірігуі де салынған деп саналады.
- Егер екi фигура салынса, онда олардың айырмасы кұр жиын болу-болмауын анықтауға болады.
- Егер салынған екi фигураның айырмасы кұр жиын болмаса, онда бұл айырма да салынған.
- Егер екi фигура салынса, онда олардың қимасы кұр жиын болатын -болмайтынын анықтауға болады
- Егер салынған екi фигураның қимасы кұр жиын болмаса, онда бұл қима да салынған болып есептеледi.
- Тұрғызылған екi фигураның кез-келген саны шектi ортақ нүктелерiн салуға болады, егер олар бар болса.
- Тұрғызылған фигураға тиiстi нүктенi салуға болады, егер олар бар болса.
- Тұрғызылған фигураға тиiстi емес нүктенi салуға болады.
Конструктивтi геометрияның негiзгi талаптары (постулаттар) сызба жұмысының ең басты кезеңдерiн абстрактылы түрде бейнелейдi. Олар дәлелсiз қабылданған аксиомалар болып табылады және конструктивтi геометрияны логикалық негiздеуде қолданылады. Постулаттарды салу қадамдары деп те атайды. Олар мыналар:
П1. Тұрғызылған екі нүкте арқылы түзу салу.
П2. Берілген нүктені центр етіп алып, берілген радиуспен шеңбер салу.
П3. Тұрғызылған параллель емес екі түзудің қиылысу нүктесін салу
П4. Егер тұрғызылған шеңбер мен түзу қиылысатын болса, олардың қиылысу нүктесін салу.
П5. Егер тұрғызылған екі шеңбер қиылысса, олардың қиылысу нүктесін салу.
Қарапайым есептердің шешулерін негізгі салуларға келтіру үшін де көптеген логикалық қадамдар жасауға тура келеді. Ал қиынырақ есептерді шешудің логикалық структурасын тұрғызу одан да қиынға соғады. Сондықтан күрделі есептерде қарапайым салу есептерін біле отырып, салу қадамдарын үнемдеуімізге болады, яғни қарапайым салуларды болашақта негізгі салуларға келтірмей - ақ қолдана аламыз.
- Салу есептерін шешу кезеңдері
Оқу жағдайында конструктивті есептерді шешу кезінде келесі төрт кезеңнен тұратын схеманы қолдану ұсынылады:
1. Талдау
2. Салу
3. Дәлелдеу
4. Зерттеу
1. Талдау. Бұл салу есептерін шешудің ең негізгі және «әзірлеуші» бөлімі, себебі мәселені шешудің кілті осында. Талдаудың мақсаты - қажетті элементтер мен берілгендер арасындағы байланысты тағайындау арқылы есепті шешудің жолдарын табу. Біз оған берілген және қажетті фигураларды тапсырманың шартында көрсетілген орынға орналастыратын көмекші сурет көмегімен қол жеткіземіз. Бұл сызбаны «қолмен» салуға болады. Әдетте, талдау «мәселе шешілді делік» деген сөздерден басталады.
2. Салу. Бұл бөлімде негізгі салулардың тізімі (немесе бұрын шешілген) келтірілген, соның нәтижесінде қажетті фигура алынады. Суреттің әр қадамы көрсетілген құралдың көмегімен графикалық түрде бейнелейді.
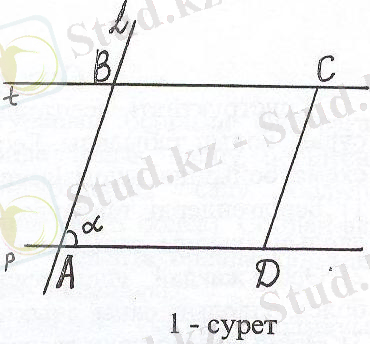 Мысалы, көршілес екі қабырғасы және олардың арасындағы бұрышы бойынша параллелограмм салу есебінің салу жоспары төмендегіше болады (1-сурет) :
Мысалы, көршілес екі қабырғасы және олардың арасындағы бұрышы бойынша параллелограмм салу есебінің салу жоспары төмендегіше болады (1-сурет) :
1) кез - келген р түзуі
2) АD∈р кесіндісі
3) ∠DАL=α бұрышы (α-берілген)
4) АВ∈АL кесіндісі (берілген қабырға)
5) В нүктесі арқылы t // р түзуі
6) ВС=АD, ВС∈t кесіндісі
7) С, D нүктелерін қосамыз
АВСD-ізделінді параллелограмм.
3. Дәлелдеу. Дәлелдеудің мақсаты - сіз cызған формула шынымен берілген есеп талаптарына сәйкес келетіндігін көрсету. Салудың әр кезеңі орындалатының дәлелі әдетте сөйлем түрінде беріледі. Дәлелдемелерде біз мыналарды қарастырамыз: талдаудың салдары дәлелдеудің шарты болып табылады, ал керісінше, талдаудың шарты дәлелдемелердің салдары болып табылады.
4. Зерттеу. Салу есептері бір ғана шешімін құрумен шектеледі және ондағы барлық қадамдар орындалады деп қабылданады.
Тапсырманы толық шешу үшін мынадай мәселелерді анықтау қажет:
- Әрдайым (яғни кез келген деректерді таңдау кезінде) таңдаулы тәсілмен құрастыруды орындауға бола ма?
- Егер таңдалған тәсілді қолдануға болмайтын болса, іздеген кескінді қалай салуға болады және қалай салынады?
- Әрбір мүмкін деректерді таңдау кезінде қанша шешімге ие
Есепті осындай талқылау нәтижесінде қажетті суретті көрсетілген жолмен салу мүмкіндігі пайда болады. Сұрақ туындайды: "егер салуда қандай да бір өзгерістер болса, есептің жаңа шешімдері пайда бола ма?" Кейде есептің әр шешімі бұрын анықталған шешімге сәйкес келетіндігін дәлелдеуге болады. Егер солай болса, қосымша зерттеулердің қажеті жоқ. Егер сәйкессіздік дәлелденсе, ол басқа әдіспен анықталды. Шешімдер болуы мүмкін болғандықтан, талдауға оралу арқылы берілген немесе ізделінді фигураларды орналастырудың басқа жағдайлары қарастырылады. Есеп жеткілікті қарапайым болған кезде талдау немесе зерттеу сияқты кейбір кезеңдер қарастырылмайды.
Енді осы салу есептерінің кезеңдеріне мысал келтірейік
Есеп 1: р периметрі мен іргелес α, β бұрыштары бойынша үшбұрыш салу.
Шешуі:
 Талдау:
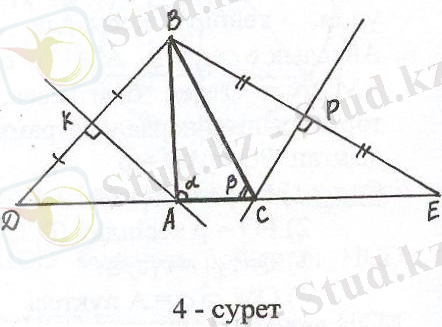
Айталық ВС - ізделінді үшбұрыш (4 - сурет),
Талдау:
Айталық ВС - ізделінді үшбұрыш (4 - сурет),
АВ + ВС + СА = р
және ∠ВАС = α, ∠ВСА = β.
Егер АС табанының созындысына АD = AB,
CE = BC болатындай кесінділер белгілесек,
DE кесіндісінің ұзындығы периметрге тең
болады, яғни DE = p . D, E нүктелерін АВС
үшбұрышының В төбесімен қосамыз.
Сонда DBA және EBC тең бүйірлі үшбұрыш-
тары шығады. Үшбұрыштың сыртқы бұрышының қасиетін ескерсек, ∠ADB = ∠ABD =
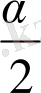 , ∠CBE = ∠CEB =
, ∠CBE = ∠CEB =
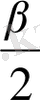 . Демек DEB үшбұрышы бір қабырғасы және оған іргелес екі бұрышы бойынша белгілі.
. Демек DEB үшбұрышы бір қабырғасы және оған іргелес екі бұрышы бойынша белгілі.
Салу:
1) DЕВ үшбұрышы (DE =
p
, ∠BDE =
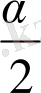 , ∠BED =
, ∠BED =
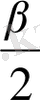 ) .
) .
- DB кесіндісінің орта перпедикуляры: n1
3) DE ∩ n 1 = A нүктесі
4) BЕ кесіндісінің орта перпедикуляры: n 2
5) DE ∩ n 2 = В нүктесі
6) АВ, СВ кесінділері
∆ АВС - ізделінді.
Дәлелдеу: n 1 , n 2 орта перпендикулярлар болғандықтан, сәйкесінше АВ = AD, BC = CE. Ал салу бойынша DA + AC + CE = p , бұдан АВ + АС + ВС = р .
Егер n 1 ∩ DB = K, n 2 ∩ EB = P десек,
∠KAD = 90
0
-
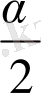 , ∠PCE = 90
0
-
, ∠PCE = 90
0
-
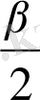 .
.
Дәл осылайша, ∠KAВ = 90
0
-
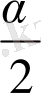 , ∠PCВ = 90
0
-
, ∠PCВ = 90
0
-
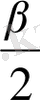
Сонда
∠ВАС = 180
0
- ∠В АD = 180
0
- ∠KAВ - ∠KAD = 180
0
- 90
0
+
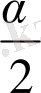 - 90
0
+
- 90
0
+
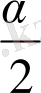 =
=

∠ВСA = 180
0
- ∠BCE = 180
0
- ∠PCB - ∠PCE = 180
0
- 90
0
+
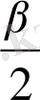 - 90
0
+
- 90
0
+
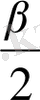 =
=
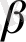
Зерттеу: α + β < π шарты орындалғанда есептің шешімі бар және ол жалғыз болады. Себебі, қарсы жорып, А′В′С′ үшбұрышы да шешім болады десек, ∠В′А′С′ = α, ∠В′С′А′ = β, А′В′ + В′С′ + С′А′ = р , онда ∆АВС = ∆А′В′С′.
Есеп 2: АВСD тіктөртбұрышы берілген. Оның СD қабырғасынан АВМ, BCM, ADM үшбұрыштары ұқсас болатындай етіп, М нүктесін табыңыз.
Шешуі:
Талдау: Есеп шешілді, яғни ізделінді М нүктесі тұрғызылды делік (8-сурет) . Онда АВМ, BCM, ADM үшбұрыштарының ұқсастықтарын және ∠С=∠D=90 0
екенін ескеріп, ∠АМВ = 90
0
теңдігін аламыз. Ал тікбұрышты үшбұрышқа сырттай сызылған шеңбердің қасиетін пайдалансақ М
 ω, мұндағы ω-диаметрі АВ болатын шеңбер.
ω, мұндағы ω-диаметрі АВ болатын шеңбер.
Салу: 1) О - АВ кесіндісінің ортасы
2) ω (О, ОВ) шеңбері
3) ω ∩ DC = М нүктесі
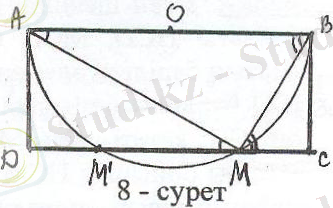 М - ізделінді нүкте.
М - ізделінді нүкте.
Дәлелдеу:
М
 ω ⇒ ∠АМВ = 90
0
, ал ∠А = ∠В = 90
0
екенін ескерсек, ∠МАВ = 90
0
- ∠МАD = ∠АМD, дәл осылайша ∠МВА = ∠ВМС. Онда
ω ⇒ ∠АМВ = 90
0
, ал ∠А = ∠В = 90
0
екенін ескерсек, ∠МАВ = 90
0
- ∠МАD = ∠АМD, дәл осылайша ∠МВА = ∠ВМС. Онда
 АМВ ∼
АМВ ∼
 АМD ∼
АМD ∼
 ВМС.
ВМС.
Зерттеу: Салу жоспарының 3) қадамына байланысты мына жағдайлар болу мүмкін:
- ВС < ОВ, онда ω ∩ DC қимасы М және М′ нүктелерінен құралады да, есептің екі шешімі болады.
- ВС = ОВ, онда ω ∩ DC = М - жалғыз нүкте, олай болса, есептің бір ғана шешімі бар.
- ВС > ОВ, онда ω ∩ DC = ∅, яғни есептің шешімі жоқ.
Кейбір геометриялық салуларды тек бір құралдың көмегімен де шешуге болады. Мысалы, тек циркульдың көмегімен шешілетін салу есебін қарастырайық:
Есеп 3: Тек циркульды пайдаланып, берілген тікбұрышты үшбұрышқа іштей шеңбер сызыңыз.
Шешуі:
 Талдау:
Айталық АВС - катеттері
а, в
, гипотенузасы
с
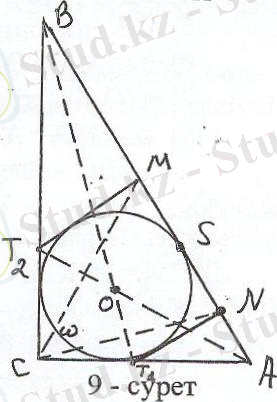
болатын берілген тікбұрышты үшбұрыш, ал ω - оған іштей сызылған ізделінді шеңбер (9-сурет) .
Талдау:
Айталық АВС - катеттері
а, в
, гипотенузасы
с
болатын берілген тікбұрышты үшбұрыш, ал ω - оған іштей сызылған ізделінді шеңбер (9-сурет) .
Центрі А, радиусы в болатын шеңбер жүргізіп,
Оның гипотенузамен қимасын М деп, ал центрі
В, радиусы а болатын шеңбердің гипотенузамен
қимасын N деп белгілесек, онда МN = BN - BM=
a - (c - в) = a + в - c.
Бұл сан үшбұрышқа іштей сызылған шеңбердің
диаметрі болады (есептен кейінгі ескертуде
дәлелденіп көрсетіледі) . Олай болса MN кесіндісін
екіге бөлу арқылы ізделінді шеңбердің радиусын
аламыз. Ал оның центрін табу үшін оның катеттерден
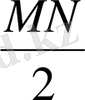 қашықтықта жататынын және (S, SN) шеңберіне тиістілігін ескереміз, мұндағы S - іштей сызылған шеңбердің гипотенузамен жанасу нүктесі.
қашықтықта жататынын және (S, SN) шеңберіне тиістілігін ескереміз, мұндағы S - іштей сызылған шеңбердің гипотенузамен жанасу нүктесі.
Салу: 1) ω 1 (А, в ) шеңбері
2) ω 2 (В, а ) шеңбері
3) ω 1 ∩ АВ = М нүктесі
4) ω 2 ∩ АВ = N нүктесі
5) ω 3 (N, MN) шеңбері
6) ω 4 (M, MN) шеңбері
 7) ω
3
∩ ω
4
= D нүктесі (D - АВС
7) ω
3
∩ ω
4
= D нүктесі (D - АВС
үшбұрышының сыртындағы нүкте)
8) ω 5 (D, MN) шеңбері
9) ω 5 ∩ ω 3 = E нүктесі (М - нан өзге)
10) ω 6 (Е, MN) шеңбері
11) ω 6 ∩ ω 3 = F нүктесі (D - дан өзге)
12) ω 7 (F, MF) шеңбері
13) ω 7 ∩ ω 4 = L, K нүктелері
14) ω 8 (K, MN) шеңбері
15) ω 9 (L, MN) шеңбері
16) ω 8 ∩ ω 9 = S нүктесі (М - нан өзге)
17) ω 10 (S, SM) шеңбері
18) ω 11 (C, SN) шеңбері
19) ω 11 ∩ CA = R нүктесі
20) ω 12 (R, CR) шеңбері
21) ω 12 ∩ ω 10 = O нүктесі
ω(O, MS) - ізделінді шеңбер
Дәлелдеу:
ω
10
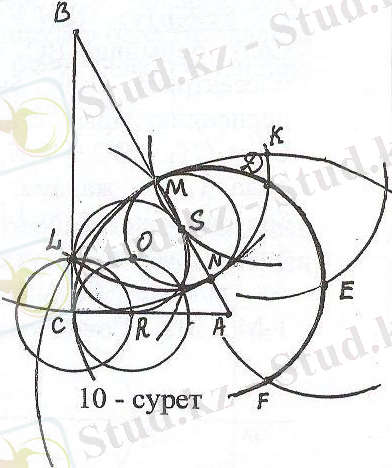
шеңберінен SM = SO = SN (S - шеңбердің центрі, ал M, O, N оның бойындағы нүктелер (10-сурет) ) . Онда SM = SO = SN =
 = r, яғни OS = r. Салу бойынша OR = r, онда АС - жанама ⇒ АС ⊥ OR және АС ⊥ ВС ⇒ ORBC. О нүктесінен ОТАС түзуін жүргізсек (Т ∈ ВС), ТОRС - тіктөртбұрыш. Ал OR = CR = r болғандықтан, TORC- квадрат, яғни OT=CR=r. Демек ω(O, MS) немесе ω(O, OR) - ізделінді шеңбер.
= r, яғни OS = r. Салу бойынша OR = r, онда АС - жанама ⇒ АС ⊥ OR және АС ⊥ ВС ⇒ ORBC. О нүктесінен ОТАС түзуін жүргізсек (Т ∈ ВС), ТОRС - тіктөртбұрыш. Ал OR = CR = r болғандықтан, TORC- квадрат, яғни OT=CR=r. Демек ω(O, MS) немесе ω(O, OR) - ізделінді шеңбер.
Зерттеу: а < с, в < с болғандықтан, салу жоспарының 1) - 15) қадамдары бірмәнді орындалады. К нүктесінен АВ қабырғасына түсірілген перпен-дикулярдың табанын Р деп белгілесек, 16) салу орындалу үшін МК > РК шарты орындалу керек.
MF > MN ⇒ PK > DS.
MD =
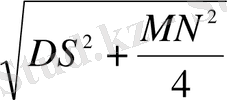 ⇒ 2MD =
⇒ 2MD =
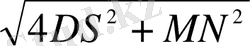 және MD = MN ⇒
және MD = MN ⇒
DS =
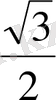 MN немесе DS =
MN немесе DS =
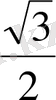 MK.
MK.
PK >
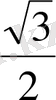 MK, онда MK <
MK, онда MK <
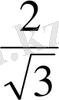 PK.
PK.
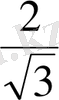 > 1, сондықтан МК > РК. Олай болса, ω
8
∩ ω
9
= S нүктесі табылады. Қалған салу қадамдары да бірмәнді. Сонымен көрсетілген тәсілмен шешілген есептің жалғыз шешеімі бар және басқа әдіспен шешкенде өзге шешімнің болуы мүмкін емес, өйткені үшбұрышқа тек бір ғана шеңбер іштей сызылады.
> 1, сондықтан МК > РК. Олай болса, ω
8
∩ ω
9
= S нүктесі табылады. Қалған салу қадамдары да бірмәнді. Сонымен көрсетілген тәсілмен шешілген есептің жалғыз шешеімі бар және басқа әдіспен шешкенде өзге шешімнің болуы мүмкін емес, өйткені үшбұрышқа тек бір ғана шеңбер іштей сызылады.
Ескерту: MN = 2r, яғни MN = d екенін дәлелдейік (9-сурет) . Салу бойынша BC = BN болғандықтан, ВТ 1 - әрі медиана, әрі биссектриса, әрі биіктік, онда ВТ 1 - CN кесіндісінің орта перпендикуляры, яғни СТ 1 = T 1 N. Онда СВNT 1 төртбұрышында BN + CT 1 = BC + T 1 N, яғни ω - СВNT 1 төртбұрышына іштей сызылған, онда Т 1 N - жанама. Дәл осылайша Т 2 М түзуі де ω шеңберіне жанама болады. Енді Т 1 N Т 2 М екенін дәлелдейік. Т 1 ∈ в және СТ 1 ⊥ ВС болғандықтан, Т 1 нүктесінен АВ-ға дейінгі қашықтық СТ 1 болады. Ал дәлелдеу бойынша СТ 1 = T 1 N, онда T 1 N ⊥ MN. Дәл осылайша Т 2 М ⊥ MN. Сонда соңғы екі қатынастан Т 1 N Т 2 М, онда MN = d.
ІІ тарау. Салу есептерін шешу әдістері
Салу есептерін шешудің бірнеше әдістері бар. Оларға:
- Нүктелердің геометриялық орны әдісі
- Түрлендірулер әдісі (параллель көшіру, осьтік симметрия, центрлік симметрия, бұру, ұқсас түрлендіру, гомотетия)
- Алгебралық әдісі
- Инверсия әдісі жатады.
Нүктелердің геометриялық орны
Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің мәнісі мынада: айталық, салу есебін шешкенде екі шартты бірдей қанағаттандыратын Х нүктесін табу керек болсын. Бірінші шартты қанағат-тандыратын нүктелердің геометриялық орны қайсыбір Ғ 1 фигурасы болады, ал екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ 2 фигурасы болады. Ізделінді Х нүктесі Ғ 1 фигурасына да, Ғ 2 фигурасына да тиісті, яғни олардың қиылысу нүктесі болып табылады. Егер бұл гео-метриялық орындар қарапайым болса (мысалы, түзулер мен шеңберлерден құралса), біз оларды сала аламыз және қажетті Х нүктесін тауып алуға болады.
НГО сызық немесе бірнеше сызықтардың бірігуі ғана емес, сонымен қатар нүктелердің жиыны, жазықтықтың бөлігі, т. б. болу мүмкін. Кейде көрсетілген қасиетті қанағаттандыратын НГО болмайды.
Геометриялық салулардың ішінде НГО-нын табу есептері жиі кездеседі. Мұндай есептерде кейбір «қарапайым» немесе «элементар» фигуралардың бірігуі белгілі деп алынып, осы бірігудің қай элементі ізделінді ГО-ды қанағаттандыратанын тауып, көрсету керек. НГО табу есептерін шешу методикасы талдау, салу, дәлелдеу және зерттеуден тұрады.
Мысал: Бір қабырғасы, сол қабырғаға қарсы жатқан сүйір бұрышы және іштей сызылған шеңбердің радиусы бойынша үшбұрыш салыңыз.
Шешуі:
Талдау: Есеп шешілді делік, АВС - ізделінді үшбұрыш, ВС, ∠ВАС және r берілген элементтер (14 - сурет) .
Айталық О - іштей сызылған шеңбердің центрі. ВС түзуін кез - келген етіп алып, одан кез - келген ВС кесіндісін белгілеу оңай. Содан соң О нүктесін тұрғызсақ, ізделінді үшбұрыштың А төбесі оңай табылады. Олай болса, О нүктесі негізгі элемент болып табылады.
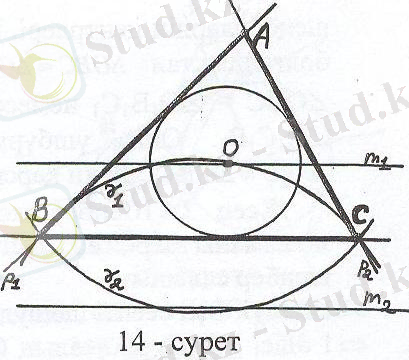 ВОС үшбұрышынан
ВОС үшбұрышынан
∠ВОС +
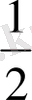 ∠АВС +
∠АВС +
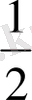 ∠АСВ = 180
0
⇒ ∠ВОС = 180
0
-
∠АСВ = 180
0
⇒ ∠ВОС = 180
0
-
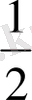 (180
0
- ∠A) = 90
0
-
(180
0
- ∠A) = 90
0
-
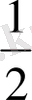 ∠A ⇒ ∠ВОС = 90
0
-
∠A ⇒ ∠ВОС = 90
0
-
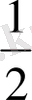 ϕ,
ϕ,
мұндағы ϕ = ∠ВАС және ϕ< 90 0 .
Сонымен О нүктесі мына екі шартты қанағаттандырады:
α 1 ) ол ВС түзуінен берілген r қашықтықта жатады;
α
2
) ВС кесіндісі О нүктесінен 90
0
-
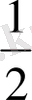 ϕ бұрышымен көрінеді.
ϕ бұрышымен көрінеді.
α 1 шартын қанағаттандыратын нүктелердің жиыны (F 1 деп белгілейік) ВС түзуіне параллель екі түзуден құралады (1. 2., 2 0 ), ал α 2 шартын қанағаттан-дыратын нүктелердің жиыны (F 2 деп белгілейік) ұштары ортақ А, В нүктелері болатын екі доғадан тұрады (1. 2., 6 0 ) .
Салу: 1) ВС кесіндісі
2) α 1 ) шартын қанағаттандыратын түзулер: m 1 , m 2
3) α 2 ) шартын қанағаттандыратын доғалар: γ 1 , γ 2
4) m 1 ∩ γ 1 = О нүктесі
5) ω = (О, r) шеңбері
6) В нүктесінен ω - ға р 1 жанамасы
7) С нүктесінен ω - ға р 2 жанамасы
8) р 1 ∩ р 2 = А нүктесі
9) АВ, АС кесінділері
 АВС - ізделінді.
АВС - ізделінді.
Дәлелдеу:
Салу бойынша ω АВС үшбұрышына іштей сызылған. Енді ∠ВАС = ϕ екенін дәлелдеу керек. ∠ВОС = 90
0
-
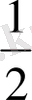 ϕ (салу бойынша), сондықтан ВОС үшбұрышынан
ϕ (салу бойынша), сондықтан ВОС үшбұрышынан
∠ВОС +
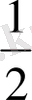 ∠АВС +
∠АВС +
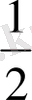 ∠АСВ = 180
0
⇒
∠АСВ = 180
0
⇒
90
0
-
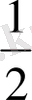 ϕ +
ϕ +
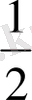 (∠АВС + ∠АСВ) = 180
0
⇒
(∠АВС + ∠АСВ) = 180
0
⇒
ϕ + ∠АВС +∠АСВ = 180 0 ⇒ ∠ВАС = ϕ
Зерттеу:
F
1
, F
2
жиындарының ортақ нүктесі болу үшін
 сtg (45
0
+
сtg (45
0
+
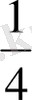 ϕ) ≥ r (1)
ϕ) ≥ r (1)
шарты орындалуы керек. Бұл АВС үшбұрышының салынуының қажетті шар-ты болады. Енді оның жеткілікті шарт болатынын дәлелдейік. Шынымен де, (1) шарты орындалса, салу жоспарының 1) - 5) қадамдары әрдайым салынады.
(р 1 , ^ ВС) + (р 2 , ^ ВС) = ∠АВС +∠АСВ = 180 0 - ϕ,
ал ϕ < 90 0 , онда р 1 , р 2 түзулері қиылысады да, А нүктесі бар болады және біреу. Демек есептің жалғыз шешімі бар.
Қарсы жориық, АВС және А
1
В
1
С
1
- есеп шартын қанағаттандыратын үшбұрыштар, ал О
1
, О
2
- сәйкесінше оларға іштей сызылған шеңберлердің центрлері. ВС = В
1
С
1
, ∠ВОС = ∠В
1
О
1
С
1
және BH = В
1
Н
1
болғандықтан
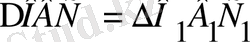 , мұнда ВН, В
1
Н
1
- биіктіктер. Онда ∠ОВС = ∠О
1
В
1
С
1
немесе ∠АВС = ∠А
1
В
1
С
1
. Дәл осылайша ∠АСВ = ∠А
1
С
1
В
1
. Онда үшбұрыштар теңдігінің екінші белгісі бойынша
, мұнда ВН, В
1
Н
1
- биіктіктер. Онда ∠ОВС = ∠О
1
В
1
С
1
немесе ∠АВС = ∠А
1
В
1
С
1
. Дәл осылайша ∠АСВ = ∠А
1
С
1
В
1
. Онда үшбұрыштар теңдігінің екінші белгісі бойынша
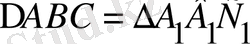 . Яғни қарсы жору қате, есептің жалғыз шешімі болады.
. Яғни қарсы жору қате, есептің жалғыз шешімі болады.
Алгебралық әдіс
Кейбір геометриялық салуларда түзудің қандай да бір кесіндісін тұрғызу керектігі айтылады. Ондай есептерді шешу үшін алгебралық әдісті қолданамыз.
Алгебралық әдіс бойынша берілген кесінділердің ұзындықтары а, в, с, . . . әріптерімен, ізделінді кесіндінің ұзындығы х әрпімен белгіленіп алынады да, есеп шартын пайдалана отырып ізделінді кесінділердің ұзындығын берілгендермен байланыстыратындай теңдеу құрылады. Құрылған теңдеуді шешіп, х-тің табылған өрнегінің геометриялық кескінін саламыз. Бұл - ізделінді кесінді болады.
Кейбір кесінділерді (немесе бірнеше кесінділерді) салу арқылы салу есептерін шешу алгебралық әдіс деп аталады. Салу есептерін шешудің алгебралық әдісі төмендегі алгоритм арқылы іске асады:
- теңдеу құру
- құрылған теңдеуді шешу
- формуланы зерттеу
- табылған кесіндіні салу.
Мысал: «Бірлік» кесінді берілген. Ұзындығы у =
 санына тең болатын кесіндіні тұрғызу керек. Ізделінді кесіндіні салу үшін у - ті ондық бөлшек түрінде өрнектеп, содан соң түзуге ондық, жүздік және т. б. бөліктеріне сәйкес бірлік кесіндіні өлшеп саламыз. Алайда ізделінді кесіндіні бұлай салу дәл болмайды. Оны циркуль мен сызғышты пайдалану арқылы «дәл» тұрғызудың басқа әдісі бар. Ол туралы төменде айтылады.
санына тең болатын кесіндіні тұрғызу керек. Ізделінді кесіндіні салу үшін у - ті ондық бөлшек түрінде өрнектеп, содан соң түзуге ондық, жүздік және т. б. бөліктеріне сәйкес бірлік кесіндіні өлшеп саламыз. Алайда ізделінді кесіндіні бұлай салу дәл болмайды. Оны циркуль мен сызғышты пайдалану арқылы «дәл» тұрғызудың басқа әдісі бар. Ол туралы төменде айтылады.
Қарапайым формулалармен берілген кесінділерді салу
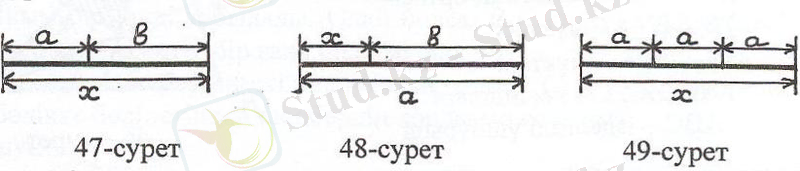
І. х = а + в Салу 47-суретте көрсетілген.
ІІ. х = а - в (а>в) Салу 48-суретте көрсетілген.
 ІІІ.
х =
nа
,
n
∈ Ν. Бұл кесіндіні салу І-ші салуға келтіріледі. Мысалы 49-суретте
n
= 3 болған жағдай белгіленген: х = 3
а
.
ІІІ.
х =
nа
,
n
∈ Ν. Бұл кесіндіні салу І-ші салуға келтіріледі. Мысалы 49-суретте
n
= 3 болған жағдай белгіленген: х = 3
а
.
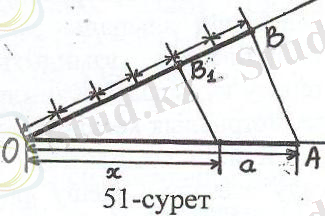
ІV.
х =
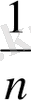 a
. Бұл кесіндіні салу үшін берілген
а
кесіндісінің ұшынан сәуле жүргізіп, осы сәулеге ОВ =
nв
болатындай
в
кесіндісін
n
рет саламыз да (50-сурет), В нүктесін А нүктесімен (
а
ке -
a
. Бұл кесіндіні салу үшін берілген
а
кесіндісінің ұшынан сәуле жүргізіп, осы сәулеге ОВ =
nв
болатындай
в
кесіндісін
n
рет саламыз да (50-сурет), В нүктесін А нүктесімен (
а
ке -
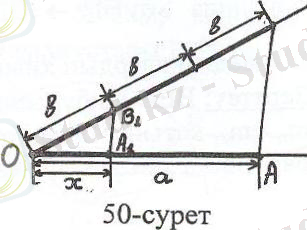
сіндісінің екінші ұшы) қосамыз. ОВ 1 = в шарты
арқылы анықталатын В 1 нүктесінен АВ - ға
жүргізілген параллель түзудің а кесіндісімен
қиылысуын А 1 десек, ОА 1 - ізделінді кесінді.
V.
х =
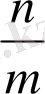 a
,
n, m
- берілген натурал сандар,
а
- берілген кесінді. Бұл кесіндіні екі әдіспен салуға болады:
a
,
n, m
- берілген натурал сандар,
а
- берілген кесінді. Бұл кесіндіні екі әдіспен салуға болады:
1) а кесіндісін бірдей m бөлікке бөліп (жо-
ғардағы ІV салу), алынған кесіндіні n есе
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz