Байланыссыз сынамалар үшін бір факторлы дисперсияталдау

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

7.3. Байланыссыз сынамалар үшін бір факторлы дисперсияталдау

Әдістің мақсаты
Бір факторлы дисперсті талдау әдісі өзгеріп жатқан жағдайлардың немесе фактордың градацияларының әсерінен тиімді белгілердің өзгеруі зерттелетін терифтік) қолданылады.
Талдаудың бұл түрінің параметрлік емес нұсқасы N Kruscal-Wallis критерийі болып табылады.
Әдістің сипаттамасы
Жұмысты жеке мәндердің бағандары түрінде деректерді ұсыну арқылы бастаймыз. Әрбір баған зерттелетін жағдайлардың біреуіне немесе екіншісіне сәйкес келеді (7.2-кестені қараңыз).
Осыдан кейін бағандардағы жеке мәндерді қорытындылау керек және квадратқа дейінгі сома керек.
Әдістің мәні осы квадрат сомалардың сомасын бүкіл эксперимент барысында алынған барлық мәндер квадраттарының қосындысымен салыстыру болып табылады.
___________
4 Екі градация болуы мүмкін, бірақ бұл жағдайда біз нөлдік емес тәуелділіктерді орната алмаймыз және неғұрлым қатаң критерийлерді пайдалану орынды сияқты (2 және 3-тарауларды қараңыз).

Гипотеза
H0: Факторлардың градациялары арасындағы айырмашылықтар (әр түрлі жағдайлар) әр топтың ішіндегі кездейсоқ айырмашылықтардан артық емес.
Н1: Факторлардың градациялары арасындағы айырмашылықтар (әр түрлі жағдайлар) әр топтың ішіндегі кездейсоқ айырмашылықтардан әлдеқайда айқын байқалады.
Байланысты емес үлгілерге арналған әдістің графикалық көрінісі
7.2 суретте көрсетілімнің әр түрлі жылдамдықтарымен сөз ойнату көлемінің өзгеру қисығын көрсетеді (мысалды қараңыз). Диссиденттік талдау әдісі осы қисықпен көрсетілген үрдістің қандай артық екенін немесе сызбада белгілердің өзгеру диапазондары ретінде әр топтағы ең төменгі мәннен ең жоғарғы мәнге дейін схемалық түрде бейнеленген белгілердің шеңберін анықтауға мүмкіндік береді.

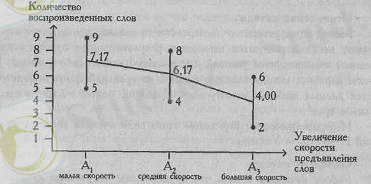
7.2 - сурет. Сөз жасау жылдамдығының артуына қарай ойнау көлемінің өзгеру қисығы; әрбір шарт белгі өзгерісінің диапазондарын көрсетеді (Greene J., D'Olivera M., 1989)

Байланысты емес үлгілер үшін бір факторлы дисперсияға шектеулер

1, Бір факторлы дисперсиялық талдау коэффициентінің кемінде үш градациясын және әрбір градацияда кемінде екі сыналатын сыналушыны талап етеді.
2, Дисперсті кешеннің әрбір ұяшығындағы дисперсиялардың теңдігі ережесі сақталуы тиіс. Дисперсияның тең шарты ұсынылған есептік схеманы теңестіру арқылы ескере отырып жүргізіледі
әр жағдайдағы бақылаулар саны (градация). Бұл әдістемелік техниканың заңдылығын Г.Шефф (1980) ақтады.
3.Алынған белгі қалыпты түрде алынған сынамада бөлінуі тиіс.
Алайда, әдетте, ол I белгіні барлық зерттелетін іріктемеде немесе дисперсиялық кешен болып табылатын іріктеменің бөлігінде бөлу мәселесі болып табылатыны көрсетілмейді.
Өзіне тән, шетелдiк басшылықтар, тұтастай алғанда, дисперсиялық талдау үшiн деректердi қалыпты бөлу қажеттiгiне сiлтеме жасай отырып, осы үшiн нақты схемалар мен мысалдарды қайтармайды және тұтас немесе дисперсиялық кешен бөлiгiнде белгiнi ң бөлiгiн бөлу туралы деректер келтiрмейдi (см; McCall R., 1970; Вельковиц Ж., Эвен Р.B, Коэн Дж., 1982; Грин Дж., Д'Оливра М., 1989).
J.Greene, M.D'Olivera (1989) нұсқаулығында ұсынылған бір факторлы емес үлгілерге қатысты дисперсияны осы авторлардың мысалын пайдалана отырып қарастырыңыз.
Мысал
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.