Мәндес түрлендірулер арқылы теңсіздіктерді шешудің әдістемесі


Академик Е. А. Бөкетов атындағы Қарағанды университеті «математика және ақпараттық технологиялар» факультеті
Математика және Информатиканы оқыту әдістемесі кафедрасы
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: Теңсіздіктерді шешуде мәндес түрлендірулерді пайдалану әдістемесі
МАЗМҰНЫ
КІРІСПЕ . . . …. .
І. ТЕҢСІЗДІКТЕР ШЕШУДІҢ СТАНДАРТ ТӘСІЛДЕРІ
1. 1 Теңсіздіктер және олардың қасиеттері . . .
1. 2 Теңсіздік ұғымының анықтамасын . . .
1. 3 Теңсіздікті оның мүшелерін жуықтап бағалау тәсілі . . .
ІІ. ТЕҢСІЗДІКТЕРДІ ШЕШУДІҢ СТАНДАРТ ЕМЕС ТӘСІЛДЕРІ
2. 1 Теңсіздікті оның мүшелерін жуықтап бағалау тәсілі . . .
2. 2 Тенсіздіктердің аналитикалық тәсілі . . .
2. 3 Теңсіздіктердің синтетикалық тәсілі . . .
2. 4 Теңсіздіктердің дұрыстығын қарсы жору әдісі . . .
2. 5 Қиындығы жоғары теңсіздіктерге туындыны қолдану . . .
3 ОРТА МЕКТЕПДЕГІ ТЕҢСІЗДІКТЕРДІ ШЕШУ ЖОЛДАРЫ
3. 1 Логарифмдік теңсіздіктерді шешу . . .
3. 2 Көрсеткіштік теңсіздіктер . . .
3. 3 Бір айнымалылы квадрат теңсіздіктер . . .
3. 4 Қарапайым тригонометриялық теңсіздіктер . . .
3. 5 Рационал теңсіздіктер интервалдар әдісі . . .
ҚОРЫТЫНДЫ . . .
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . .
КІРІСПЕ
Ел басшысы Н. Ә. Назарбаевтың "Қазақстан экономикалық, әлеуметтік тұрғыдан - "атты Қазақстан халқына Жолдауында XXI ғасырда өз білімін дамыта алмаған ел бір орында тұрғаны анық. Біздің болашағымыздың жоғары технологиялық ғылыми әзірлемелері. өндірістер мен мекемелер үшін біз мамандар қорын құруымыз керек. Қазақстанның жоғары оқу орындары қарапайым стандарттар деңгейінде білім беруге тиіс. Жетекші оқу орындарының дипломдары бүкіл әлемде танылуы тиіс. Олар мұны істеуге міндетті. Бірақ бәрі мектептен басталады " - деген.
Мектеп-бұл оқушының жеке басы мен санасының дамуы қуатты болатын ерекше құнды, ерекше кезең, өйткені дәл осы мектепте болашақтың, сауатты және сау адамның әртүрлі қасиеттері қалыптасады.
Сондықтан балалардағы математикалық білімді дамытудың бір әдісі-мәселені тұжырымдау. Мәселені тұжырымдау оқушылардың логикалық ойлауын теориялық тәжірибемен, оқумен өмірмен байланыстыруға, математикалық ұғымдарды қалыптастыруға және т. б. мүмкіндік береді. мәселені тұжырымдау арқылы балалар танымдық және тәрбиелік тұрғыдан маңызды факторлармен танысады.
Зерттеу мақсаты: - математика сабақтарындағы теңсіздіктерді стандартты және стандартты емес тәсілдермен дәлелдеу арқылы оқушылардың ойлауын дамыту әдістемесін ғылыми негіздеу және әзірлеу.
Зерттеудің өзектілігі: - егер оқушылардың ойлау қабілеті стандартты және стандартты емес тәсілдермен теңсіздіктерді дәлелдеу арқылы дамитын болса, онда олардың математика бойынша білім деңгейі артады, өйткені пәнге қызығушылық қалыптасады .
Зерттеудің ғылыми жаңалығы: - математика сабағындағы теңсіз-діктерді стандартты және стандартты емес тәсілдермен дәлелдеу арқылы оқушылардың ойлауын дамыту жолдары мен әдістерін ғылыми негіздеу.
Зерттеу нысаны -оқушылардың математиканы оқыту процесі.
Зерттеу пәні -математика сабағындағы теңсіздіктерді стандартты және стандартты емес тәсілдермен дәлелдеу арқылы оқушылардың ойлауын дамыту жолдары мен әдістері.
Зерттеу міндеттері -
1. зерттеу тақырыбымен байланысты әдебиеттермен танысу және оларға ғылыми-әдістемелік шолу беру;
2. Математика сабағындағы теңсіздіктерді стандартты және стандартты емес тәсілдермен дәлелдеу арқылы оқушылардың ойлау қабілетін дамыту мүмкіндіктерін дамыту;
3. математика сабағындағы теңсіздіктерді стандартты және стандартты емес тәсілдермен дәлелдеу арқылы оқушылардың ойлауын дамытудың әдістемесі мен тиімділігін тексеру.
Зерттеудің практикалық құндылығы келесілерден тұрады: - Математиканы оқыту; пәндерді оқыту әдістемесін жетілдіру; арнайы курстарда, студенттердің педагогикалық практикасында көмекші құрал ретінде математика мамандығы студенттерінің математиканы оқыту әдістемесін қолдану.
Дипломдық жұмыстың құрылымы: кіріспеден, үш негізгі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
І. ТЕҢСІЗДІКТЕР ШЕШУДІҢ СТАНДАРТ ТӘСІЛДЕРІ
1. 1 теңсіздіктер және олардың қасиеттері
Теңсіздіктер келесі белгілердің біреуін
 (үлкен),
(үлкен),
 (үлкен немесе тең; кем емес),
(үлкен немесе тең; кем емес),
 (Кіші),
(Кіші),
 (Кіші немесе тең; Көп емес),
(Кіші немесе тең; Көп емес),
 0 (теңсіздік) құрайтын екі өрнек (сандар)
теңсіздіктер
деп аталады.
0 (теңсіздік) құрайтын екі өрнек (сандар)
теңсіздіктер
деп аталады.
Екі жағы бірдей алгебралық өрнектер болып табылатын теңсіздіктер алгебралық теңсіздіктер деп аталады.
Мына теңсіздіктер жұбы
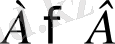 және
және
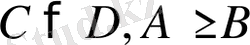 және
және
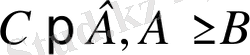 және
және
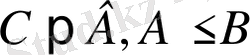 және
және
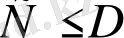 қарама-қырсы мағынадағы теңсіздіктер деп аталады.
қарама-қырсы мағынадағы теңсіздіктер деп аталады.
Ал мына теңсіздіктер жұбы
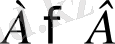 және
және
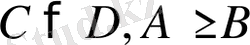 және
және
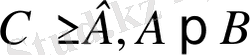 және
және
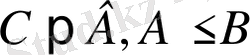 және
және
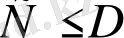 бірдей мағынадағы теңсіздіктер деп аталады.
бірдей мағынадағы теңсіздіктер деп аталады.
Мысалы, 8
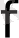 4 және 9
4 және 9
 6 - бірдей мәні бар теңсіздіктер, , ал
6 - бірдей мәні бар теңсіздіктер, , ал
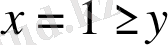 және
және
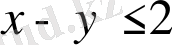
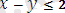 қарама-қарсы мәні бар теңсіздіктер.
қарама-қарсы мәні бар теңсіздіктер.
Мұнда
 және
және
 белгілер қатаң деп аталады, ал ал
белгілер қатаң деп аталады, ал ал

 және
және

 белгілер қатаң емес теңсіздіктер деп аталады.
белгілер қатаң емес теңсіздіктер деп аталады.
Нақты сандар өрісі тапсырыс беру қасиетіне ие: кез-келген екі нақты санның біреуі екіншісінен үлкен немесе оған тең немесе одан аз. Бұл қатыстыларды
 таңбаларымен анықтайды. Егер нақты сандар болса, онда олардың арасында
таңбаларымен анықтайды. Егер нақты сандар болса, онда олардың арасында
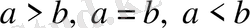 осы қатынастардың біреуі ғана орындалады.
осы қатынастардың біреуі ғана орындалады.
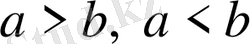 қатыстарын теңсіздіктер дейді.
қатыстарын теңсіздіктер дейді.
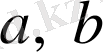 ол теңсіздіктің мүшелері делінеді.
ол теңсіздіктің мүшелері делінеді.
 деген,
деген,
 мен
мен
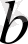 -ның айырымы оң сан,
-ның айырымы оң сан,
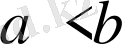 деген
деген
 мен
мен
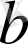 -ның айырымы теріс сан деген сөз.
-ның айырымы теріс сан деген сөз.
 мен
мен
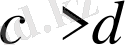 теңсіздіктерін бір мағыналы, ал
теңсіздіктерін бір мағыналы, ал
 мен
мен
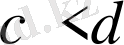 теңсіздіктерін қарама-қарсы мағыналы теңсіздіктер дейді. Олар қатаң теңсіздіктер болады.
теңсіздіктерін қарама-қарсы мағыналы теңсіздіктер дейді. Олар қатаң теңсіздіктер болады.
Олармен қатар, қатаң емес
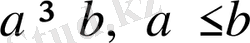 теңсіздіктер қарастыры-лады.
теңсіздіктер қарастыры-лады.
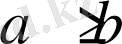 теңсіздігі
теңсіздігі
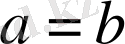 болғанда да,
болғанда да,
 болғанда да дұрыс, ал
болғанда да дұрыс, ал
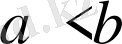 болғанда дұрыс емес.
болғанда дұрыс емес.
 ,
,
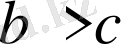 екі теңсіздіктің орнына
екі теңсіздіктің орнына
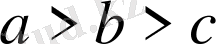 немесе
немесе
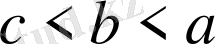 қос теңсіздігін пайдалануға болады. Сандық теңсіздіктердің мынадай қасиеттері бар:
қос теңсіздігін пайдалануға болады. Сандық теңсіздіктердің мынадай қасиеттері бар:
- Егерболса, ондаболады. Бұл теңсіздіктің қайтымсыздық қасиеті.
- Егерболса, онда кез келгенүшінболады.
- Егерболса, ондаболады. (Бұл теңсіздіктің транзитивтік қасиеті) .
- Егерболса, ондаболады.
- Егерболса, ондаболады.
Егер
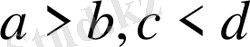 болса, онда
болса, онда
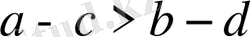 болады.
болады.
- Егерболса, онда кез .
- Егерболса, ондаболады.
- Егерболса, ондаболады.
- Егерболса, онда кез келген натурал санүшінболады. , ондаболады.
- Егерболса, онда кез келген натурал санүшінболады.
- Егерболса, онда кез келген натурал санүшінболады.
- Егерболса, онда кез келген натурал санүшінболады.
Сан модуліне арналған кейбір теңсіздіктерді дәлелдейік.
- Кез келгенсаны үшінболады.
Шешуі:
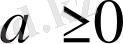 болса, онда
болса, онда
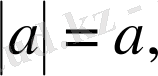 ал
ал
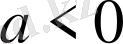 болса, онда
болса, онда
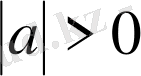
болатындықтан
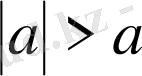 қатаң теңсіздігі орындалады. Сонымен
қатаң теңсіздігі орындалады. Сонымен
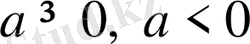 болған екі жағдай үшін
болған екі жағдай үшін
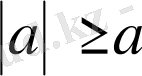 болады.
болады.
- Кез келгенжәнесандары үшінболады.
Шешуі: 13 бойынша
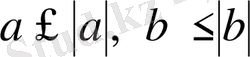 болады, оларды қоссақ 5
болады, оларды қоссақ 5
қасиет бойынша:
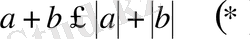 болып шығады. Ал,
болып шығады. Ал,
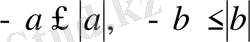 болғандықтан, қоссақ
болғандықтан, қоссақ
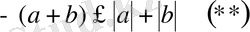 .
.
Сонда
 мен
мен
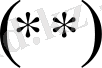 -ден
-ден
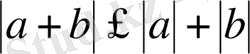
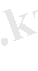 болады. Мұндағы
болады. Мұндағы
теңдік
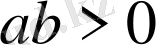 болғанда орын алады.
болғанда орын алады.
15. Кез келген
 және
және
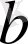 сандары үшін
сандары үшін
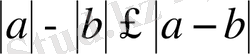 болады.
болады.
Шешуі:
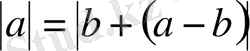 болады. Бұған 14 пайдалансақ:
болады. Бұған 14 пайдалансақ:
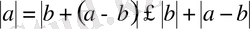 , бұдан
, бұдан
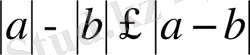 .
.
Екі нақты санды өзара салыстыру үшін түрлі әдістер қолданылады.
- Егер екі бүтін сан берілсе, онда олардың қайсысының екіншісінен үлкен не кіші екенін ажырату тікелей анықталады.
- Екі бөлшек сандарды салыстыру үшін, олардың не алымдарын, не бөлімдерін бірдей күйге келтіру керек.
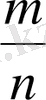 және
және
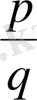 бөлшектерін ортақ бөлімге
бөлшектерін ортақ бөлімге
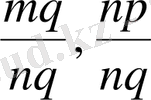 келтірсек және
келтірсек және
 болса, онда
болса, онда
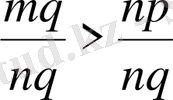 болар еді де, қысқартқаннан соң
болар еді де, қысқартқаннан соң
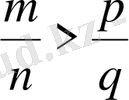 болып шығады.
болып шығады.
1-мысал.
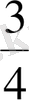 және
және
 бөлшектерін салыстыру үшін, ортақ бөлімге
бөлшектерін салыстыру үшін, ортақ бөлімге
келтіреміз
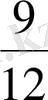 және
және
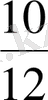 .
.
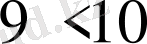 болғандықтан
болғандықтан
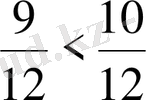 , бұдан
, бұдан
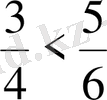
болады.
3. Түбірлерді (радикалдарды) салыстыру үшін, түбірлердің дәрежелерін теңестіріп, түбір астындағы санды салыстыру керек.
Мәселен,
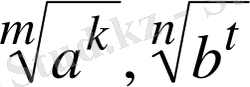 болса, мына
болса, мына
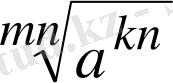 және
және
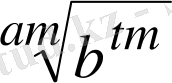 күйге келтіріп
күйге келтіріп
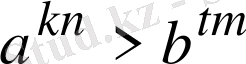 болса, онда
болса, онда
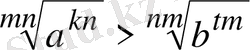 болады да,
болады да,
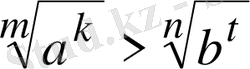 болып шығады.
болып шығады.
2-мысал.
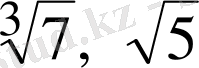 түбірлерін салыстыру үшін, түбір дәрежелерін,
түбірлерін салыстыру үшін, түбір дәрежелерін,
тең күйге келтіреміз. Сонда
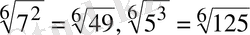 болып
болып
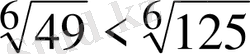 болғандықтан
болғандықтан
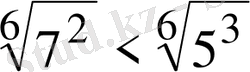 , бұдан
, бұдан
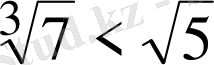 болып
болып
шығады.
- Логарифмді салыстырғанда мыналарды ескеру керек:
а)
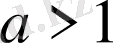 болғанда, егер
болғанда, егер
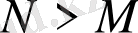 болса,
болса,
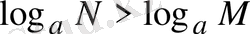 болады.
болады.
б)
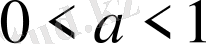 болғанда, егер
болғанда, егер
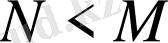 болса
болса
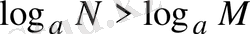 болады.
болады.
3-мысал.
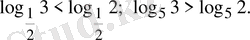
Бірінші теңсіздікте
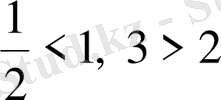 , екінші теңсіздікте
, екінші теңсіздікте
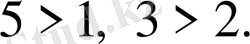
4-мысал.
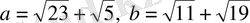 . Егер
. Егер
 деп жорысақ, онда
деп жорысақ, онда
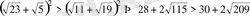 болар еді. Түрлендірсек
болар еді. Түрлендірсек
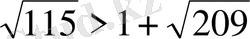 болар еді.
болар еді.
Бұл теңсіздік дұрыс емес, сондықтан
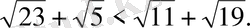 Дәл осы есепті былайша да салыстыруға болады, әр түбірді жеке-жеке бағалаймыз:
Дәл осы есепті былайша да салыстыруға болады, әр түбірді жеке-жеке бағалаймыз:
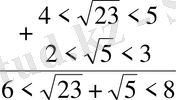
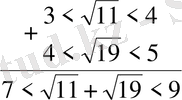
Бұдан қай түбірлер қосындысының үлкен екендігі байқалмайды. Өйткені 6 мен 8-дің арасында жатқан сан 7 мен 9-дың арасында жатқан саннан кіші болады деуге болмайды. Мәселен, бірінші 7, 9 екіншісі 7, 5 болуы мүмкін. Сондықтан, енді ол қосылғыштарды 0, 1 дәлдікте бағалаймыз.
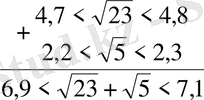
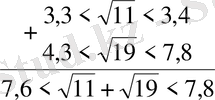
Бұдан екінші қосылғыштың көп екені көрінеді, оның аз мәнінің өзі бірінші қосылғыштың артығымен алынған мәнінен көп болып кетті:
Сонымен
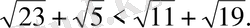
5-мысал
.
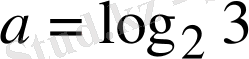 және
және
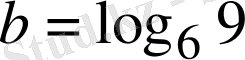 сандарын салыстыру
сандарын салыстыру
керек:
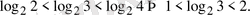
Ал,
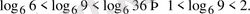
Сонымен
 мен
мен
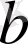
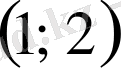 аралықта жатыр екен.
аралықта жатыр екен.
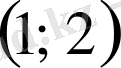 аралықтың қақ ортасы
аралықтың қақ ортасы
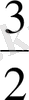 . Берілген сандар
. Берілген сандар
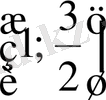 немесе
немесе
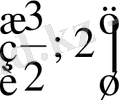 аралықтың қайсысында жататынын анықтаймыз:
аралықтың қайсысында жататынын анықтаймыз:
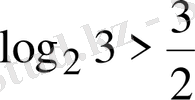 дейік, онда
дейік, онда
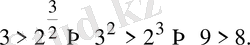
Бұл дұрыс теңсіздік. Сондықтан
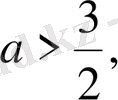 яғни
яғни
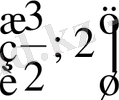 аралықта жатады екен.
аралықта жатады екен.
Енді
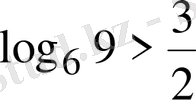 дейік, онда
дейік, онда
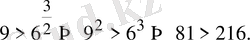 Бұл дұрыс емес теңсіздік. Сондықтан
Бұл дұрыс емес теңсіздік. Сондықтан
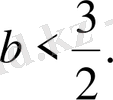 Сонымен
Сонымен
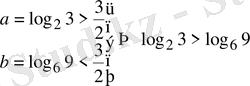 болып шығады.
болып шығады.
6-мысал
.
 және
және
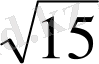 сандарын салыстырыңдар:
сандарын салыстырыңдар:
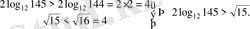
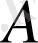 және
және
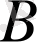 алгебралық өрнектердің мүмкін мәндері облысына кіретін
алгебралық өрнектердің мүмкін мәндері облысына кіретін
 жиынынан алынған сандарға сай келетін
жиынынан алынған сандарға сай келетін
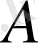 өрнегінің сан мәні сол сандарға сай келетін
өрнегінің сан мәні сол сандарға сай келетін
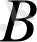 өрнегінің сан мәнінен үлкен (кіші) болатын болса,
өрнегінің сан мәнінен үлкен (кіші) болатын болса,
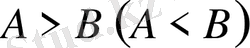 теңсіздігі
теңсіздігі
 жиынында теңбе-тең теңсіздік делінеді.
жиынында теңбе-тең теңсіздік делінеді.
Мысалы:
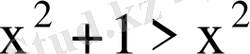 теңсіздігі нақты сандар жиынында теңбе-тең теңсіздік болады, өйткені
теңсіздігі нақты сандар жиынында теңбе-тең теңсіздік болады, өйткені
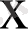 -тың кез келген нақты мәнінде бұл теңсіздік дұрыс теңсіздік.
-тың кез келген нақты мәнінде бұл теңсіздік дұрыс теңсіздік.
Егер
 жиыны берілмесе, онда теңбе-тең теңсіздік ол теңсіздікке кіретін өрнектердегі мүмкін мәндері жиынында қарастырылады.
жиыны берілмесе, онда теңбе-тең теңсіздік ол теңсіздікке кіретін өрнектердегі мүмкін мәндері жиынында қарастырылады.
Алгебралық өрнектерде де қатаң теңсіздіктермен
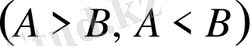 қатар, қатаң емес теңсіздіктер
қатар, қатаң емес теңсіздіктер
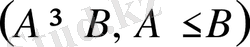 қарастырылады. Қатаң емес
қарастырылады. Қатаң емес
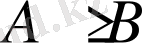 теңсіздікте бұл өрнектердің мүмкін мәндері облысына кіретін
теңсіздікте бұл өрнектердің мүмкін мәндері облысына кіретін
 жиынынан алынған сандарға сай келетін
жиынынан алынған сандарға сай келетін
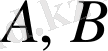 өрнектерінің сан мәндері не тең, не
өрнектерінің сан мәндері не тең, не
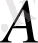 -ның сан мәні
-ның сан мәні
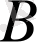 -ның сан мәнінен үлкен деп түсіну керек.
-ның сан мәнінен үлкен деп түсіну керек.
Теңбе-тең теңсіздіктердің мынадай қасиеттері бар.
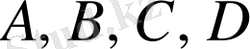 алгебралық өрнектерінің мүмкін мәндері облысынан алынған
алгебралық өрнектерінің мүмкін мәндері облысынан алынған
 жиынында:
жиынында:
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады.
- болса, ондаболады. -натурал сан.
- болса, ондаболады. -натурал сан.
- болса, ондаболады. -натурал сан.
- болса, ондаболады. -натурал сан.
- болса, ондаболады. -натурал сан.
- болса, ондаболады. -натурал сан.
Бұл келтірілген қасиеттер
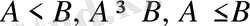 теңсіздіктері үшін де дұрыс. Көптеген жағдайда теңсіздіктердің берілген жиынында немесе ол теңсіздіктерге кіретін алгебралық өрнектердің мүмкін мәндері жиыны облысында теңсіздіктердің дұрыс, не қате екенін дәлелдеуге тура келеді.
теңсіздіктері үшін де дұрыс. Көптеген жағдайда теңсіздіктердің берілген жиынында немесе ол теңсіздіктерге кіретін алгебралық өрнектердің мүмкін мәндері жиыны облысында теңсіздіктердің дұрыс, не қате екенін дәлелдеуге тура келеді.
Дәлелдеу түрлі жолмен іске асады. Ол жолдардың кейбіреулеріне мысалдар келтірейік.
1. 2 Теңсіздік ұғымының анықтамасын
Теңсіздіктің анықтамасы бойынша
 болу ұшін
болу ұшін
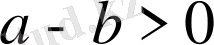 болуы жеткілікті. Сондықтан
болуы жеткілікті. Сондықтан
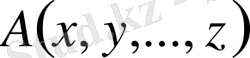 және
және
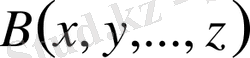 алгебра-лық өрнектері үшін
алгебра-лық өрнектері үшін
 екенін көрсету үшін
екенін көрсету үшін
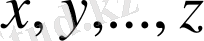 айнымалылар-дың қарастырылып отырған жиыннан алынатын кезкелген сан мәндері үшін
айнымалылар-дың қарастырылып отырған жиыннан алынатын кезкелген сан мәндері үшін
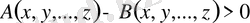 екенін дәлелдеу керек.
екенін дәлелдеу керек.
1-мысал.
Таңбалас кез келген екі нақты санның бір-біріне қатынастарының қосындысы 2 -ден кем болмайтындығын, яғни
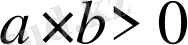 болса, онда
болса, онда
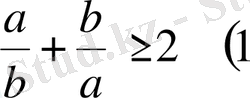 болатындығын дәлелдеңіздер?
болатындығын дәлелдеңіздер?
Шешуі: Мына айырымды қарастырамыз.
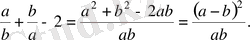
Бұл өрнек
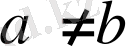 болса оң, ал
болса оң, ал
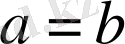 болса нөлге тең. Сондықтан
болса нөлге тең. Сондықтан
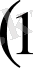 дұрыс теңсіздік.
дұрыс теңсіздік.
2-мысал
. Екі оң нақты санның арифметикалық ортасы, сол сандардың геометриялық ортасынан кем болмайды, яғни
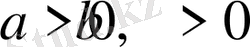 болса, онда
болса, онда
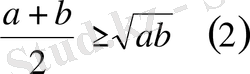 болады(Коши теңсіздігі) .
болады(Коши теңсіздігі) .
Шешуі . Айырымын қарастырамыз.
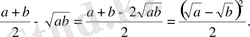
Соңғы өрнек кез келген
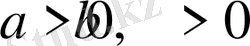 сандары үшін оң, ал
сандары үшін оң, ал
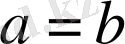 болса нөл. Сондықтан
болса нөл. Сондықтан
 теңсіздік дұрыс.
теңсіздік дұрыс.
3-мысал
. Оң сан үшін
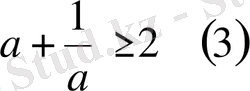 болатындығын шешіңіз.
болатындығын шешіңіз.
Шешуі
Айырымы
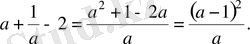
Бұл кез келген
 үшін оң сан. Сондықтан
үшін оң сан. Сондықтан
 теңсіздік дұрыс. Тепе-теңдік тек
теңсіздік дұрыс. Тепе-теңдік тек
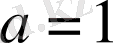 болғанда орындалады.
болғанда орындалады.
4-мысал
.
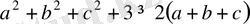 теңсіздігін дәлелдеңіздер.
теңсіздігін дәлелдеңіздер.
Шешуі
. Айырма
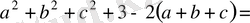
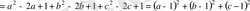
кезкелген нақты сан
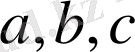 үшін оң сан болады. Сондықтан,
үшін оң сан болады. Сондықтан,
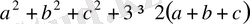 дұрыс теңсіздік.
дұрыс теңсіздік.
5-мысал
. Кез келген оң сандар үшін
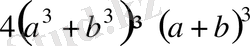 теңсіздігінің дұрыстығын дәлелдеңіздер.
теңсіздігінің дұрыстығын дәлелдеңіздер.
Шешуі
.
Айырым
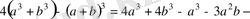
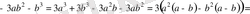
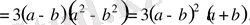
Бұл кез келген
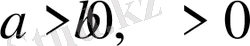 үшін оң сан. Сондықтан берілген теңсіздік дұрыс.
үшін оң сан. Сондықтан берілген теңсіздік дұрыс.
Берілген сандар жиынында қарастырылатын теңсіздіктің екі жағының да сандық мағынасы болатын теңсіздіктің құрамына енетін әріптердің мүмкін мәндерін теңсіздіктің мүмкін мәндері деп атайды.
Мысал-1. Теңсіздіктің мүмкін мәндерін табыңдар:
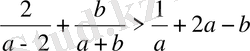 .
.
Шешуі
. Егер
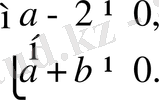 яғни
яғни
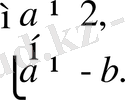 болса, онда теңсіздіктің сол жағының мағынасы болады. Егер
болса, онда теңсіздіктің сол жағының мағынасы болады. Егер
 болса, теңсіздіктің оң жағының мағынасы болады.
болса, теңсіздіктің оң жағының мағынасы болады.
Жауабы:
Теңсіздіктегі әріптердің мүмкін мәндері:
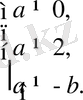
Теңсіздіктің құрамына енетін әріптердің барлық мүмкін мәндерінде дұрыс болатын теңсіздіктерді теңбе-тең теңсіздіктер деп атайды.
Анықтама
.
Егер
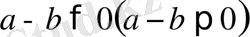 болса, онда
болса, онда
 саны
саны
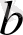 санынан үлкен (кіші) деп атайды. Оларды сәйкесінше былай жазады:
санынан үлкен (кіші) деп атайды. Оларды сәйкесінше былай жазады:
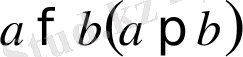
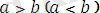 .
.
1. 3 Теңсіздіктің қасиеті
Теңсіздіктердің негізгі қасиеттері төмендегі теоремалар арқылы өрнектеледі.
Теорема 1. Егер
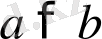 болса, онда
болса, онда
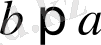 болады (
қайтымсыздық қасиеті
) .
болады (
қайтымсыздық қасиеті
) .
Шешуі:
Айталық
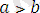
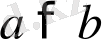 болсын, онда
болсын, онда
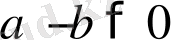 болады. Сонда
болады. Сонда
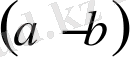 - ға қарама-қарсы сан теріс таңбалы сан болады, яғни
- ға қарама-қарсы сан теріс таңбалы сан болады, яғни
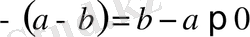 бұдан
бұдан
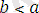
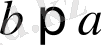 болады.
болады.
Сонымен, теңсіздіктің бұл қасиетінің дұрыстығы дәлелденді.
Теорема 2. Егер
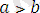
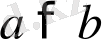 және
және
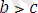
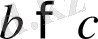 болса, онда
болса, онда
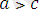
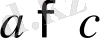 болады
(транзитивтік қасиеті) .
болады
(транзитивтік қасиеті) .
Шешуі:
Шарт бойынша
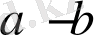 - оң таңбалы сан, және
- оң таңбалы сан, және
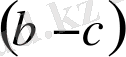 -оң таңбалы сан; олардың қосындысы
-оң таңбалы сан; олардың қосындысы
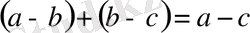
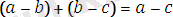 саны да оң таңбалы. Демек,
саны да оң таңбалы. Демек,
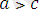
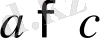 (анықтама бойынша) .
(анықтама бойынша) .
Теорема 3. Егер
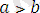
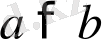 болса, онда
болса, онда
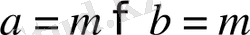
 болады.
болады.
Шешуі:
Айталық,

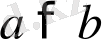 яғни
яғни
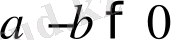
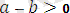 болсын. Сонда
болсын. Сонда
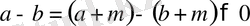
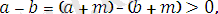 бұдан
бұдан
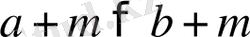
 болатындығы айқын.
болатындығы айқын.
Сонымен, теңсіздіктің бұл қасиетінің дұрыстығы да дәлелденді.
Салдар. Теңбе-тең теңсіздіктің мүшелерін оның бір жағынан екінші жағына қарама-қарсы таңбамен шығаруға болады.
Теорема 4. Егер
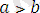
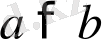 және
және
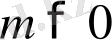
 болса, онда
болса, онда
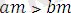
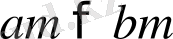 болады.
болады.
Шешуі:
Айталық,
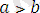
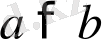 , яғни
, яғни
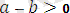
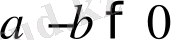 және
және

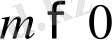 болатындықтан, екі оң санның көбейтіндісі де оң сан болады, яғни
болатындықтан, екі оң санның көбейтіндісі де оң сан болады, яғни
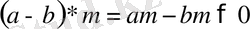
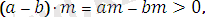 бұдан
бұдан
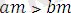
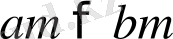 болады.
болады.
Сонымен, теңсіздіктің бұл қасиетінің дұрыстығы да дәлелденді.
Салдар. Егер
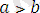
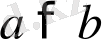 және
және

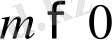 болса, онда
болса, онда
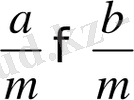
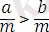 болады.
болады.
Теорема 5. Егер
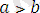
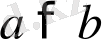 және
және

 болса, онда
болса, онда
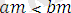
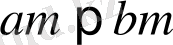 болады.
болады.
Шешуі:
Айталық,

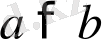 яғни,
яғни,
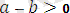
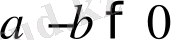 және
және

 болатындықтан, оң таңбалы сан мен теріс таңбалы санның көбейтіндісі теріс таңбалы сан болатындықтан,
болатындықтан, оң таңбалы сан мен теріс таңбалы санның көбейтіндісі теріс таңбалы сан болатындықтан,
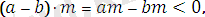
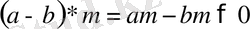 бұдан
бұдан
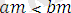
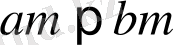 болады.
болады.
Сонымен, теңіздіктің бұл қасиетінің дұрыстығы да дәлелденді.
Салдар. Егер
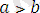
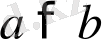 және
және

 болса,
болса,
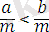
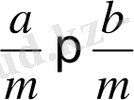 болады.
болады.
Теорема 6. Егер
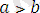
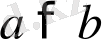 және
және
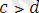
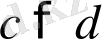 болса, онда
болса, онда
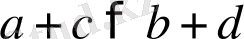
 болады, яғни бірдей мағыналы теңсіздіктерді қосқанда сондай мағыналы теңсіздік шығады.
болады, яғни бірдей мағыналы теңсіздіктерді қосқанда сондай мағыналы теңсіздік шығады.
Шешуі:
Айталық,
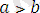
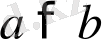 және
және
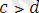
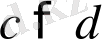 , яғни
, яғни
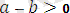
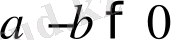 және
және
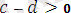
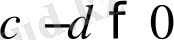 болсын. Сонда екі оң таңбалы санның қосындысы да оң таңбалы сан болатындықтан,
болсын. Сонда екі оң таңбалы санның қосындысы да оң таңбалы сан болатындықтан,
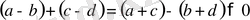
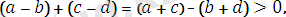 бұдан
бұдан

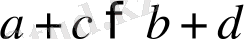 болады.
болады.
Сонымен, теңсіздіктің бұл қасиетінің дұрыстығы да дәлелденді.
Теорема 7. Егер
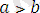
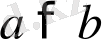 және
және
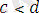
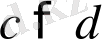 болса, онда
болса, онда
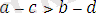
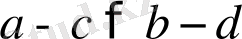 болады, яғни қарама-қарсы мағыналы теңсіздіктерді алғанда шегеретін азайғыш теңсіздікпен мағыналас теңсіздік шығады.
болады, яғни қарама-қарсы мағыналы теңсіздіктерді алғанда шегеретін азайғыш теңсіздікпен мағыналас теңсіздік шығады.
Шешуі:
Айталық,
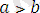
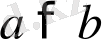 және
және

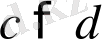 яғни
яғни
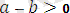
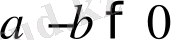 және
және
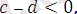
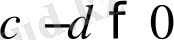 яғни
яғни
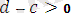
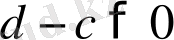 болсын. Сонда екі оң таңбалы санның қосындысы да оң сан болатындықтан,
болсын. Сонда екі оң таңбалы санның қосындысы да оң сан болатындықтан,
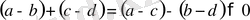
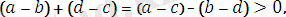 бұдан
бұдан
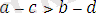
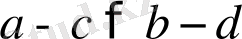 болады.
болады.
Сонымен, теңсіздіктің бұл қасиетінің дұрыстығы да дәлелденді.
Теорема 8. Егер
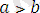
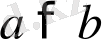 және
және

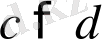 мұнда
мұнда
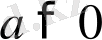 ,
,
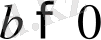 ,
,
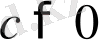 ,
,
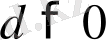
 болса, онда
болса, онда
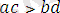
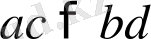 болады, яғни мүшелері оң бірдей мағыналы теңсіздіктерді көбейткенде сондай мағыналы теңсіздік шығады.
болады, яғни мүшелері оң бірдей мағыналы теңсіздіктерді көбейткенде сондай мағыналы теңсіздік шығады.
Шешуі:
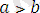
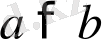 теңсіздігінің екі жағында бірдей
теңсіздігінің екі жағында бірдей
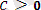
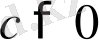 -ға көбейтіп табатынымыз:
-ға көбейтіп табатынымыз:

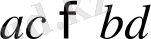
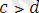
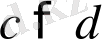 теңсіздігінің екі жағында бірдей
теңсіздігінің екі жағында бірдей
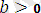
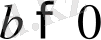 -ға көбейтіп табатынымыз:
-ға көбейтіп табатынымыз:

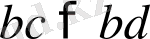
Транзитивтік қасиет бойынша
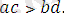
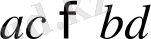
Теорема 9. Егер
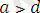
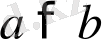 және
және
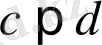
 мұнда
мұнда
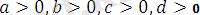
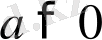 ,
,
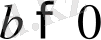 ,
,
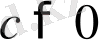 ,
,
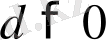 болса, онда
болса, онда
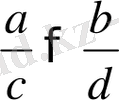
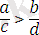 болады, яғни мүшелері оң қарама-қарсы мағыналы теңсіздіктерді мүшелеп бөлгенде бөлгіш теңсіздікке мағыналас теңсіздік шығады.
болады, яғни мүшелері оң қарама-қарсы мағыналы теңсіздіктерді мүшелеп бөлгенде бөлгіш теңсіздікке мағыналас теңсіздік шығады.
Шешуі:
Шынында да,
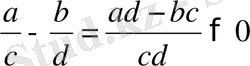
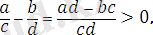 өйткені
өйткені
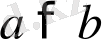 ,
,
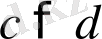
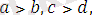 яғни
яғни
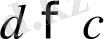
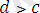 болатындықтан,
болатындықтан,
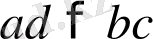
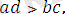 яғни
яғни
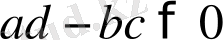
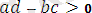 және екі оң таңбалы санның көбейтіндісі ретінде
және екі оң таңбалы санның көбейтіндісі ретінде

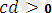 болады, олай болса,
болады, олай болса,
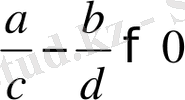
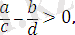 бұдан
бұдан
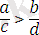
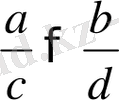 болады.
болады.
Теорема 10. Егер

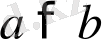 мұндағы
мұндағы
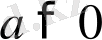 ,
,
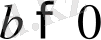 және
және
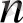 - натурал сан болса, онда
- натурал сан болса, онда
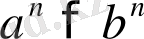
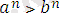 болады, яғни мүшелері оң теңсіздіктің екі жағында бірдей натурал дәрежеге шығарғанда берілген теңсіздікке мағыналас теңсіздік шығады.
болады, яғни мүшелері оң теңсіздіктің екі жағында бірдей натурал дәрежеге шығарғанда берілген теңсіздікке мағыналас теңсіздік шығады.
Шешуі:
Расында да, теңсіздіктің бұл қасиетінің дұрыстығына мағыналас теңсіздіктерді өзара мүшелеп
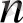 рет көбейту арқылы көз жеткізуге болады.
рет көбейту арқылы көз жеткізуге болады.
Теорема 11. Егер

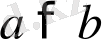 мұндағы
мұндағы
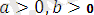
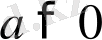 ,
,
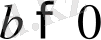 және
және
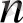 - натурал сан болса, онда
- натурал сан болса, онда
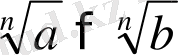
 болады, яғни мүшелері оң теңсіздіктің екі жағынан бірдей натурал көрсеткішті түбір тапқанда, берілген теңсіздікке мағыналас теңсіздік шығады.
болады, яғни мүшелері оң теңсіздіктің екі жағынан бірдей натурал көрсеткішті түбір тапқанда, берілген теңсіздікке мағыналас теңсіздік шығады.
Теореманың дұрыстығы қарсы жору әдісімен оп-оңай дәлелденеді [82] .
Теңсіздіктерді бұл тәсіл бойынша дәлелдеу «артық» және «кіші» ұғымдарының тікелей анықтамасына негізделген және теңсіздіктің сол жағы мен оң жағында тұрған айырманың таңбасын анықтауға арналған.
Бұл тәсіл бойынша
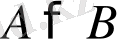
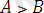 теңсіздігін дәлелдеудің орнына берілген теңсіздіктің мүмкін мәндеріне
теңсіздігін дәлелдеудің орнына берілген теңсіздіктің мүмкін мәндеріне
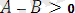
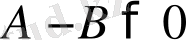 теңсіздігінің орындалатындығын көрсету жеткілікті. Ал,
теңсіздігінің орындалатындығын көрсету жеткілікті. Ал,
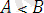
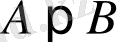 теңсіздігін дәлелдеудің орнына сәйкес
теңсіздігін дәлелдеудің орнына сәйкес
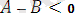
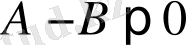 теңсіздігін дәлелдеу қажет.
теңсіздігін дәлелдеу қажет.
Сонымен, бұл тәсіл бойынша
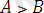
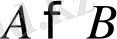 немесе
немесе
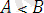
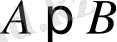 теңсіздігінің ақиқаттығын көрсету үшін
теңсіздігінің ақиқаттығын көрсету үшін
 айырмасын құрып, оның таңбасын зерттеу қажет. Сонда, егер
айырмасын құрып, оның таңбасын зерттеу қажет. Сонда, егер
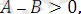
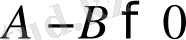 онда
онда

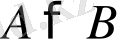 ал егер
ал егер
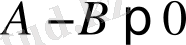
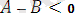 болса, онда
болса, онда
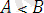
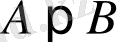 болады.
болады.
Енді осы тәсілге бірнеше мысалдар қарастырайық.
1-мысал
.
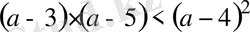 теңсіздігін шешіңіз.
теңсіздігін шешіңіз.
Шешуі.
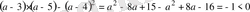 . Олай болса, берілген теңсіздік кез келген
. Олай болса, берілген теңсіздік кез келген
 үшін орындалады.
үшін орындалады.
.
2-мысал
. Кез келген
 және
және
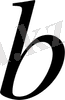 сандары үшін
сандары үшін
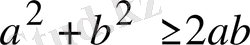 теңсіздігі орындалатынын шешіңіз.
теңсіздігі орындалатынын шешіңіз.
Шешуі:
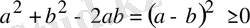 болғандықтан, берілген теңсіздік анықтама бойынша дұрыс.
болғандықтан, берілген теңсіздік анықтама бойынша дұрыс.
3-мысал
. Егер
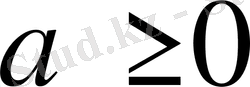 ,
,
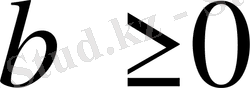 болса, онда
болса, онда
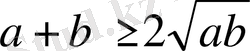 теңсіздігі орындалатынын шешіңіз.
теңсіздігі орындалатынын шешіңіз.
Шешуі:
Анықтама бойынша, егер
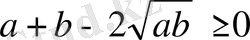 болса, онда
болса, онда
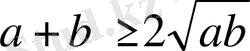 теңсіздігінің ақиқаттығы шығады:
теңсіздігінің ақиқаттығы шығады:
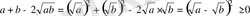 .
.
4-мысал
. Барлық
 және
және
 үшін
үшін
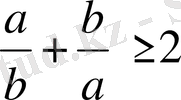 теңсіздігінің орындалатындығын шешіңіз.
теңсіздігінің орындалатындығын шешіңіз.
Шешуі:
Айырманың таңбасын анықтайық:
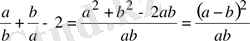 . Сонда
. Сонда
 ,
,
 болғандықтан, бұл бөлшектің теріс таңбалы емес екендігі айқын. Олай болса, егер
болғандықтан, бұл бөлшектің теріс таңбалы емес екендігі айқын. Олай болса, егер
 ,
,
 болса, онда
болса, онда
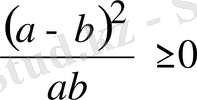 және
және
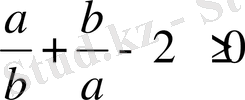 , демек,
, демек,
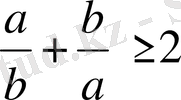 теңсіздігі орындалады.
теңсіздігі орындалады.
5-мысал
. Теңсіздікті шешіңіз:
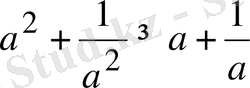 , мұндағы
, мұндағы
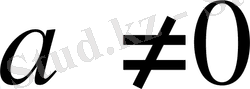 .
.
Шешуі: Айырманың таңбасын қарастырамыз:
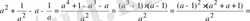
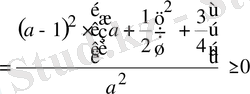 ,
,
бұл айырма
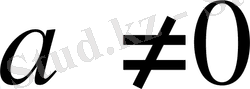 болғанда, теріс таңбалы емес. Сондықтан теңсіздіктің анықтамасы бойынша
болғанда, теріс таңбалы емес. Сондықтан теңсіздіктің анықтамасы бойынша
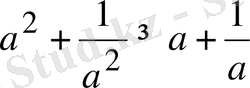 теңсіздігі ақиқат.
теңсіздігі ақиқат.
6-мысал
. Кез келген нақты
 ,
,
 ,
,
 сандары үшін
сандары үшін
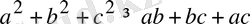 теңсіздігінің орындалатынын шешіңіз.
теңсіздігінің орындалатынын шешіңіз.
Шешуі: Теңсіздіктің екі жағын да бірдей 2-ге көбейтіп, сондағы шыққан айырманы қарастырайық:
 .
.
Олай болса,
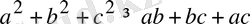 .
.
7-мысал
.
 болғанда,
болғанда,
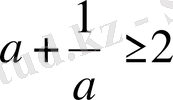 теңсіздігі орындалатынын шешіңіз.
теңсіздігі орындалатынын шешіңіз.
Шешуі:
Айырманың таңбасын қарастырамыз:
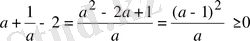 .
.
Сонда
 ,
,
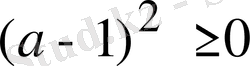 болғандықтан, бұл айырма теріс таңбалы емес. Сондықтан берілген теңсіздік анықтама бойынша дұрыс.
болғандықтан, бұл айырма теріс таңбалы емес. Сондықтан берілген теңсіздік анықтама бойынша дұрыс.
8-мысал
. Коши теңсіздігін шешіңіз:
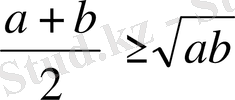 , мұндағы
, мұндағы
 ,
,
 (оң сандардың арифметикалық ортасы олардың геометриялық ортасынан кем емес) .
(оң сандардың арифметикалық ортасы олардың геометриялық ортасынан кем емес) .
Шешуі: Айырманың таңбасын қарастырамыз:
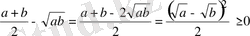 .
.
Сонда
 ,
,
 болғанда,
болғанда,
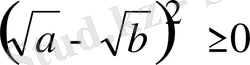 болатындықтан, бұл айырма оң таңбалы, яғни теріс таңбалы емес. Сондықтан берілген теңсіздік анықтама бойынша дұрыс.
болатындықтан, бұл айырма оң таңбалы, яғни теріс таңбалы емес. Сондықтан берілген теңсіздік анықтама бойынша дұрыс.
9-мысал
. Теңсіздікті шешіңіз:
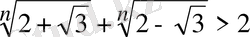 .
.
Шешуі:
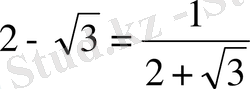 екендігін ескеріп, айырманың таңбасын анықтаймыз:
екендігін ескеріп, айырманың таңбасын анықтаймыз:
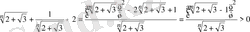 .
.
Сонда
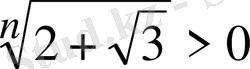 ,
,
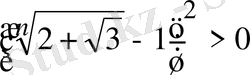 болғандықтан, бұл айырма оң таңбалы, олай болса, берілген теңсіздік анықтама бойынша дұрыс.
болғандықтан, бұл айырма оң таңбалы, олай болса, берілген теңсіздік анықтама бойынша дұрыс.
10-мысал . Теңсіздікті шешіңіз:
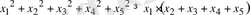 .
.
Шешуі:
Теңсіздіктің айырымын
 деп белгілеп, оның таңбасын қарастырамыз:
деп белгілеп, оның таңбасын қарастырамыз:
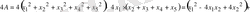
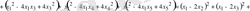
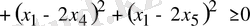 .
.
Сонда
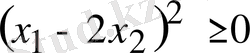 ,
,
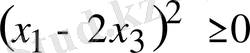 ,
,
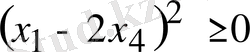 ,
,
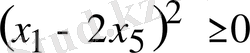 болғандықтан, бұл айырма оң таңбалы, олай болса, берілген теңсіздік анықтама бойынша дұрыс.
болғандықтан, бұл айырма оң таңбалы, олай болса, берілген теңсіздік анықтама бойынша дұрыс.
11-мысал.
Теңсіздікті шешіңіз:
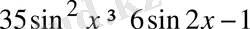 .
.
Шешуі: Айырманың таңбасын қарастырамыз:

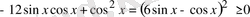 .
.
Сонда
 болғандықтан, бұл айырма теріс таңбалы емес. Олай болса, берілген теңсіздік анықтама бойынша дұрыс.
болғандықтан, бұл айырма теріс таңбалы емес. Олай болса, берілген теңсіздік анықтама бойынша дұрыс.
ІІ. ТЕҢСІЗДІКТЕРДІ ШЕШУДІҢ СТАНДАРТ ЕМЕС ТӘСІЛДЕРІ
2. 1 Теңсіздікті оның мүшелерін жуықтап бағалау тәсілі
Бұл әдісті кейде теңсіздікті «күшейту» немесе «бәсеңдету» әдісімен дәлелдеу деп те атайды. Бұл әдісте берілген теңсіздіктің мүшелерін жоғарыдан немесе төменнен бағалау арқылы дәлелдейді. Айталық, бізге
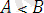
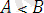 теңсіздігін дәлелдеу керек болсын. Сонда егер де біз
теңсіздігін дәлелдеу керек болсын. Сонда егер де біз
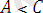
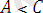 және
және
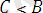
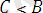 теңсіздіктерін дәлелдей алсақ, онда теңсіздіктің транзитивті қасиеті бойынша
теңсіздіктерін дәлелдей алсақ, онда теңсіздіктің транзитивті қасиеті бойынша
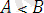
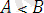 теңсіздігі дәлелденген болып шығады. Бұл әдісті теңсіздікті «күшейту» әдісімен дәлелдеу деп атайды.
теңсіздігі дәлелденген болып шығады. Бұл әдісті теңсіздікті «күшейту» әдісімен дәлелдеу деп атайды.
1-мысал
. Кез келген
 үшін
үшін
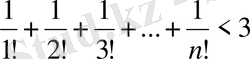 теңсіздігі орындалатындығын шешіңіз.
теңсіздігі орындалатындығын шешіңіз.
Шешуі:
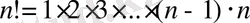 екендігін ескеріп, теңсіздіктің сол жағын бағалаймыз:
екендігін ескеріп, теңсіздіктің сол жағын бағалаймыз:
 - еселігі
- еселігі
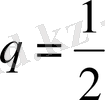 -ге тең геометриялық прогрессияның
-ге тең геометриялық прогрессияның
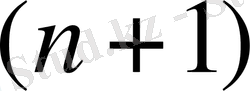 мүшесінің қосындысы. Оның қосындысы мынаған тең:
мүшесінің қосындысы. Оның қосындысы мынаған тең:
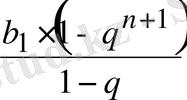 екені белгілі.
екені белгілі.
Сонда
 болғандықтан, кез келген
болғандықтан, кез келген
 үшін
үшін
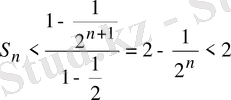 .
.
2-мысал
. Теңсіздіктің дұрыстығын шешіңіз:
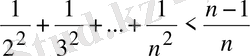 .
.
Шешуі:
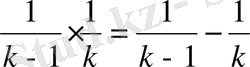 теңдігін пайдаланып табатынымыз:
теңдігін пайдаланып табатынымыз:

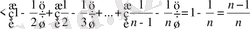 .
.
Сөйтіп,
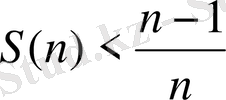 теңсіздігінің дұрыстығы дәлелденді.
теңсіздігінің дұрыстығы дәлелденді.
3-мысал
. Кез келген натурал
 саны үшін
саны үшін
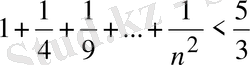 теңсіздігі орындалатындығын шешіңіз.
теңсіздігі орындалатындығын шешіңіз.
Шешуі:
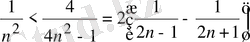 екені айқын. Сондықтан
екені айқын. Сондықтан
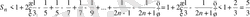 .
.
Олай болса,
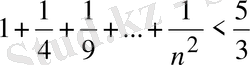 теңсіздігі ақиқат.
теңсіздігі ақиқат.
4-мысал
. Теңсіздікті шешіңіз:
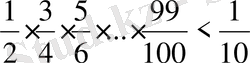 .
.
Шешуі:
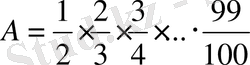 ;
;
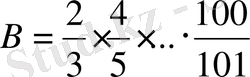 болсын.
болсын.
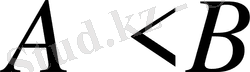 екені айқын. Сонда
екені айқын. Сонда
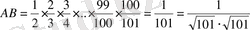 . Бұдан
. Бұдан
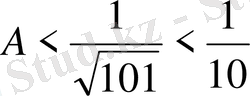 .
.
5-мысал
. Теңсіздікті шешіңіз:
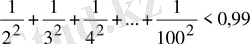 .
.
Шешуі:
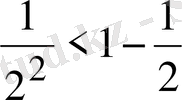 ,
,
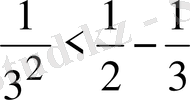 , . . . ,
, . . . ,
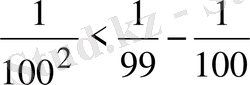 . Осы теңсіздіктерді мүшелеп қосып табатынымыз:
. Осы теңсіздіктерді мүшелеп қосып табатынымыз:
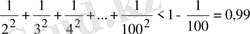 .
.
6-мысал
.
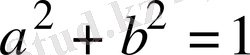 және
және
 шарттарын қанағаттандыратын кез келген нақты
шарттарын қанағаттандыратын кез келген нақты
 ,
,
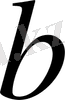 ,
,
 ,
,
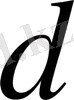 сандары үшін
сандары үшін
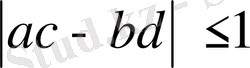 теңсіздігі орындалатындығын шешіңіз.
теңсіздігі орындалатындығын шешіңіз.
Шешуі: Теңсіздікті «күшейту» әдісі арқылы дәлелдейік. Модульдің қасиеті мен Коши теңсіздігін қолданып табатынымыз:
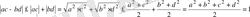 .
.
.
7-мысал
. Егер
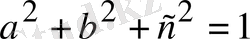 болса, онда
болса, онда
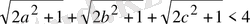 теңсіздігі орындалатындығын шешіңіз.
теңсіздігі орындалатындығын шешіңіз.
Шешуі: Коши теңсіздігін қолданып, берілген теңсіздікке енетін әрбір түбірді бағалаймыз:
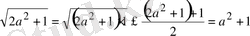 .
.
Осы сияқты,
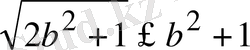 ,
,
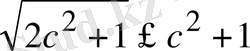 .
.
Осы теңсіздіктерді мүшелеп қосып табатынымыз:
 .
.
Берілген теңсіздіктің дұрыстығын дәлелдеу үшін соңғы теңсіздікте теңдік белгісінің орындалмайтындығын көрсетуіміз қажет.
Шынында да, теңдік белгісі мына теңдіктер бір мезгілде орындалған жағдайда ғана болуы мүмкін:
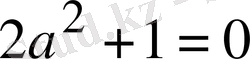 ,
,
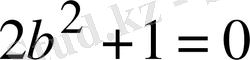 ,
,
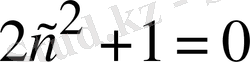 , яғни
, яғни
 ,
,
 ,
,
 болғанда.
болғанда.
Онда
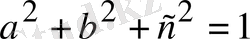 шарты орындалмайды.
шарты орындалмайды.
Сөйтіп,
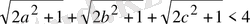 , дәлелдеу керегі де осы еді.
, дәлелдеу керегі де осы еді.
.
8-мысал
. Теңсіздікті шешіңіз:
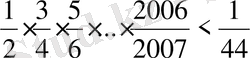 .
.
Шешуі:
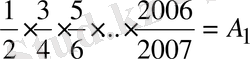 ,
,
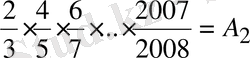 болсын. Сонда
болсын. Сонда
 ,
,
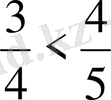 , . . . ,
, . . . ,
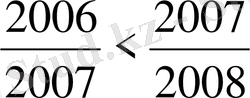 болатындықтан
болатындықтан
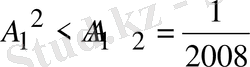 . Олай болса,
. Олай болса,
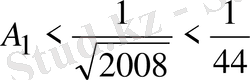 .
.
9-мысал
. Теңсіздікті шешіңіз:
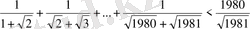 .
.
Шешуі: Әрбір қосылғыштың бөліміндегі иррационалдықты жойып табатынымыз:
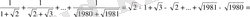
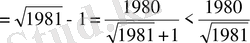 .
.
10-мысал
. Теңсіздікті шешіңіз:
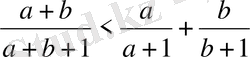 , мұндағы
, мұндағы
 ,
,
 .
.
Шешуі: Дұрыс бөлшектің қасиетін пайдаланып табатынымыз:
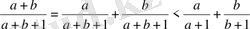 .
.
Теңсіздікті «бәсеңдету» тәсілімен дәлелдеу деп берілген теңсіздіктен оған қарағанда бәсең теңсіздікке көшу әдісін айтады. Айталық, бізге
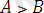
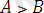 теңсіздігін дәлелдеу керек болсын. Сонда егер де біз
теңсіздігін дәлелдеу керек болсын. Сонда егер де біз
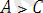
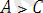 және
және
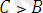
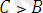 теңсіздіктерінің дұрыстығын көрсете алсақ, онда теңсіздіктің транзитивті қасиеті бойынша
теңсіздіктерінің дұрыстығын көрсете алсақ, онда теңсіздіктің транзитивті қасиеті бойынша
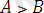
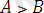 теңсіздігі дәлелденген болып шығады.
теңсіздігі дәлелденген болып шығады.
Енді осы әдіске мысалдар келтірейік.
11-мысал . Енді біз жоғарыдағы қарастырылған 6 -мысалды «бәсеңдету» әдісі арқылы дәлелдейік.
Есептің шарты бойынша
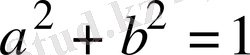 және
және
 екенін ескеріп, мынаны табамыз:
екенін ескеріп, мынаны табамыз:
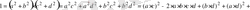
 , өйткені
, өйткені
 ,
,
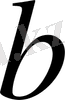 ,
,
 ,
,
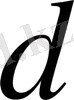 -ның кез келген нақты мәндерінде
-ның кез келген нақты мәндерінде
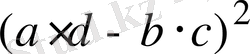 өрнегі тек теріс емес мәндер қабылдайды. Соңғы арақатыстан
өрнегі тек теріс емес мәндер қабылдайды. Соңғы арақатыстан
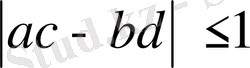 екені шығады.
екені шығады.
.
12-мысал.
Егер
 ,
,
 ,
,
 болса, онда
болса, онда
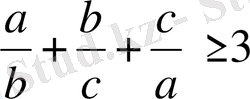 болатындығын шешіңіз. .
болатындығын шешіңіз. .
Шешуі:
Анығырақ болу үшін
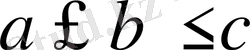 болсын.
болсын.
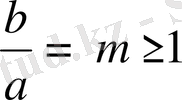 ,
,
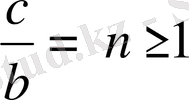 деп белгілейік.
деп белгілейік.
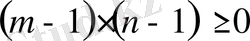 екенін ескереміз, бұдан
екенін ескереміз, бұдан
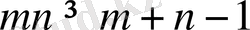 . Сонда берілген теңсіздік мынадай түрге келеді:
. Сонда берілген теңсіздік мынадай түрге келеді:
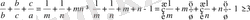 .
.
13-мысал
. Теңсіздікті шешіңіз:
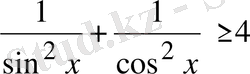 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz