Зоотехния мамандығы студенттеріне арналған биометрия негіздері


Қазақстан Республикасының білім және ғылым министрлігі
Т. К. Бексеитов, А. А. Темиржанова, М. Е. Жагипарова
БИОМЕТРИЯ НЕГІЗДЕРІ
«Зоотехния» мамандығы студенттеріне арналған
оқу құралы
УДК 57. 087. 1 (107)
ББК 28. 04я73
Б-23
С. Торайғыров атындағы ПМУ Ғылыми кеңесінің ұсынуымен
Рецензент:
ауыл шаруашылық ғылымдарының кандидаты, доцент Мустафаев Б. А.
Б-23 Т. К. Бексеитов, А. А. Темиржанова, М. Е. Жагипарова.
Биометрия негіздері: «Зоотехния» мамандығы студенттеріне арналған оқу құралы. -
Павлодар, 2007. 73 б.
Әдістемеде мал шаруашылығында негізгі биометриялық зерттеулердің әдістері, инбридинг коэфицентінің есептеу әдістері, өндірушілердің селекциялық индекстері және стандартты мәндердің математикалық кестесі берілген.
УДК 57. 087. 1 (107)
ББК 28. 04я73
© Бексеитов Т. К., Темиржанов А. А., М. Е. Жагипарова 2007
© С. Торайғыров атындағы Павлодар
мемлекеттік университеті, 2007
Мазмұны
Кіріспе . . . 3
1 Генетикалық және зооветеринарлық зерттеулер
жүйесіндегі биометрия мақсаттары мен әдістері . . . 5
2 Вариацияланатын мәндердің статистикалық талдауы . . . 12
3 Статистикалық өзара байланыс пен олардың
шамасын есептеу әдістері . . . 26
4 Дисперсиялық талдау . . . 31
5 Ұрпаққа берілу қасиеті мен қайталанудың статистикалық
талдауы . . . 35
6 Популяцияның генетикалық құрылымы және
оның өзгерістріне талдау . . . 42
7 Инбридинг. Гомозиготаның коэффициентін есептеу . . . 46 8 Асылтұқымды құдылықты анықтау әдістемесі . . . 47
9 Биометрикалық есептеулерді зоотехникалық
және ветеринарлық тәжірибе үлгісінде жүргізу . . . 49
Әдебиеттер . . . 73
Кіріспе
Зооинженер мен мал дәрігерінің шығармашылық жұмысында, тәжірибелі зерттеулер өткізу мен алынған тәжірибелерді салыстыру үлкен орын алады. Ол үшін математикалық күрделі және жай әдістер қолданылады.
Зоотехникалық тәжірибелер, мал дәрігерлік зерттеулер өткізгенде ғылыми - зерттеу институттарында, тәжірибе станциясында ғылыми бақылауда өзін кездейсоқ түрде байқатпайтын құбылыстарды анықтау қажеттілігі туындайды. Болжаулар мен ғылыми диагноздердің беріктігін анықтау, ауылшаруашылық малдарының өнімдерін пайдалану мен емдеу, азықтандыру жаңа әдістерін жаппай пайдалану ғылыми ұсыныстарын жылжыту берілген ұсыныстар мен тұжырымдар негізінде сол зерттеулердің нәтижелері анықтығын талап етеді.
Көптеген теориялық және қолданбалы тәжірбиелік зоотехникалық және малдәрігерлік жұмыстардағыдай, генетикалық талдамағада математикалық - статистикалық әдістерді пайдалануда енеді. Әрбір ғылымның даму дәрежесін, сол ғылым саласында математиканың әдістерінің қаншалықты қолданылатына қарап бағалуға болады (К. Маркс бойынша) .
Биометрия - ғылымының әдістерін қазіргі жетістіктерін пайдалану жалпы биологияда және зоотехния мен ветеринарияда математикалық статистикалық, ықтимал теория тәсілдері мен принциптерін пайдалану, жануар әлемінің тынысы мен өміріндегі жаңа табиғи құбылыстарын анықтауға мүмкіншілік жасайды. Математикалық талдау әдістері көмегімен, бар жануарлардың ерекшелігін айқындап, жеке топтағы малдардың деректерін дәл және айқын белгілейміз.
Биометрикалық талдама әдісін мал шаруашылығының мамандары мен жұмыскерлері, сондай - ақ, жоғары оқу орын студенттері мен аспиранттары, оқытушылары пайдаланады.
Қазіргі уақытта биометрия бойынша көптеген іргелі болжамдар бар, бірақта оларға теоретикалық бағыт, позициялық - математикалық талдау сипаттас, ол студенттердің жеке биометрикалық әдісті өз зерттеулерінде мен пайдалануда қиындық жасайды.
Әдістемелік ұсыныстарда биометрикалық мәндердің негізгі сипаттамасы зерттеу жұмыстарында оларды анықтау техникасы мен пайдалану саласы қарастырылады. Биометриялық есептердің алгоритмі нақты зоотехникалық және мал дәрігерлік зерттеулерде мысалдармен беріліп, негізделген зерттеулер нәтижелерімен байқалады.
Мұнда, сондай - ақ, ЭВМ - СМ - 2М биометриялық есептерді шешу бағдарламасын іске асыру режимі келтірілген.
1 Генетикалық және зооветеринарлық зерттеулер жүйесіндегі биометрия мақсаттары мен әдістері
1. 1 Биометрияның пайда болуы
Биомтерияның негізін қалаушылар болып А. Кетлэ, Ф. Гельтон, К. Пирсон саналады.
А. Кэтлэ вариациялық қатардағы орта мәндер түсінігін енгізіп, жекелей өзгерулер бойынша және қазіргі статистика негізін қалады.
Ф. Галатон регресия заңын жасады. Ол ілім қазіргі генетикада тұқымдық детерминациялы аудитивті гентүрлес тұқым коэффициенті аталып, тұқымда еркін шағылысатын популяциясы бар.
К. Пирсонның философиялық концепциясы ашығынан идеалисті болып, бірақ та, математикалық - статистикалық саласында орташа квадрат ауытқуын ашып, вариация коэффициентін, хи - квадрат әдісін, тура сызықты және қисық сызықты корреляция генетикалы - селекциялық зерттеулерде, сондай - ақ, басқадай ғылым мен техника саласында кеңінен пайдаланылады.
Ықтималдық теориясының дамуында орыстың ұлы математиктері П. Л. Чебышевтің және А. А. Чупоровтың классикалық зерттеулері үлкен маңызға ие.
Дат ғалымы В. Л. Иогансен генетикалық талдама жасаудың әдістемелік негізін салды: таза (сызықтар), математикалық өңдеу мен жасанды шағылысу.
Г. Харди (Ұлы британия) және А. Вайнберг (Германия) қазіргі популяциялық генетиканың негізін қалады.
В. Госсет ( лақап аты Стъюдент) шағын таңдау теориясын негіздеді.
Ротамстедтегі тәжірибе станциясында істеген агроном Р. А. Фишер дисперсиялық талдау әдісін ұсынды.
Ю. А. Филипченко Мендель заңының мәнді формуласы бойынша генетикалық талдауларда пайдаланатын бірқатар математикалық формулалар ұсынды.
С. С. Серебровскийдің генетикалық талдауда математикалық әдістерді орнықтырудағы еңбегі зор.
Соңғы кезде біздің елде және шет елдерде биометрия бойынша: П. Ф. Рокицкийдің «Биологиялық статистика» және «Статистикалық генетикаға кіріспе», Д. У. Снедекордің «Биология мен ауылшаруашылық зерттеулерінде пайдаланылатын статистикалық әдістері»; Н. А. Плохинскийдің «Биометрия», «Зоотехниктер үшін биометрия бойынша жетекшелігі», Е. К. Меркурьевтің «Мал шаруашылығындағы биометрия», Д. С. Фолкердің « Генетикаға сандық белгілерді енгізу», Г. Ф. Лакиннің «Биометрия» және басқадай бірқатар кітаптар мен оқулықтары баспадан шықты.
1. 2 Ықтимал теориясының негізгі түсініктері
Ықтимал теориясы зерттелетін кездейсоқ жайлармен байланысты. Зерттелетін құбылыстарға статистикалық көзқараспен түсіну үшін ықтимал теориясының кейбір түсініктері мен әдістерімен танысу қажет.
Тәжірибе - бақылау кезіңде тіркеуге мүмкіндік болатын, жайлардың іске асатын(немесе іске аспайтын) процессі. Тәжірбие барысына әсер ететін, белгілі, объективті бар немесе тәжірбиешімен жасалған құбылыстар, жағдайлар деп аталады. Осы тәжірбиеде болуы мүмкін оқиғалар нәтиже деп аталады. Берілген тәжірбиенің жағдайлары көптеген нәтижесімен бірге - сынақты құрайды.
Белгілі жағдайда міндетті түрде болатын жайлар ( нақты) сенімді деп аталады; ал болмайтын - мүмкін емес деп аталады; ал туындайтын, бірақ та туындамауы мүмкіндер - кездейсоқтық деп аталады.
Ықтималдық - қандайда бір жайдың пайда болу мүмкіншілігі дәрежесінің сандық сипаттамасы, ол шексіз сан есебінен қайталануы мүмкін.
Жайдың сенімді ықтималы бірлікке мүмкін болмайтын нольге тең.
Егер, тәжірбиеде бір жайдың пайда болуы, басқаның пайда болуына кедергі жасаса, онда олар сәйкес емес, басқадай жағдайда сәйкес деп аталады.
Кездейсоқтық қажеттіктің туындау формасы және осымен бірге ол қажеттікті толықтырушы.
Объективті кездейсоқтық туралы диалектиканың материалистік түсінігі қажеттіктің формасы ретінде табиғи құбылыстардың заңдылығын, оның ішінде өзгергіштік пен тұқым қуалаушылық құбылыстардың статистикалық заңдылықтарын дұрыс бағалауға мүмкіншілік береді.
Статистикалық заңдылықтар жеке жайлардың пайда болуы, сондай - ақ, жеке жайдың өз ықтималды пайда болуын айқындауға мүмкіндік бермейді. Статистикалық заңдылықтың басты ерекшелігі, олар белгілі жағдайлардың жиілігі мен көптеген қасиеттер бірлігін көруге көмек етеді.
Статистикалық генетикадағы кеңінен пайдаланатын, статистикалы әдістер негізіне, ықтималдық теориясы жатады. Кейбір ерекше статистикалық генетика үшін әдістер, осы жұмыстың техникалық негізін құрайды.
1. 3 Статистикалық жиынтық, оның қасиеттері, терминологиясы мен символикасы
Биометрия - ол тірі табиғат құбылыстарына тіркес математикалық статистика. Вариациялық статистика әдістері көмегімен ол өзгергіштік пен тұқым қуалауды зерттейді.
Биометрияның зерттеу нысандары болып малдар саналады, олардың өзгеруі мен белгілердің анықталу заңдылығы зерттеледі.
Өзгергіштік пен тұқым қуалау заңдылығы көп санды даналардан алынған массалық материалдармен орнатылады.
Бір - бірінен айырмашылықты және де көптеген белгілер бойынша сәйкес жекелей объектілердің әр түрлі саны, жиынтықты құрап, ол негізгі және таңдамалы боп бөлінеді.
Негізгі жиынтық дербестік құрап, ол зерттеушілерді тұқым қуалау мен өзгергіштік ерекшелігі көзқарасынан олардың белгілері қызықтырады (мысалы, бар малдардың кейбір тобын жиынтығы, толығымен тұқым немесе осы аймақ) .
Бірақ, бар малды зерттеу, сонымен қатар оларға кейбір тәжірибе өткізу, үнемі мүмкін емес, өйткені ол көптеген шығын мен уақытты қажет етеді. Сондықтан, негізгі жиынтықтың дербес бөлігін зерттейді ( тәжірибеге жатқызады) .
Таңдамалы жиынтық ( таңдау) - ол зерттеулер өткізу үшін негізгі жиынтықтан кейдесоқ таңдау әдісімен бөлінеді. Таңдау белгілі анықтық дәрежесімен барша негізгі жиынтықты сипаттайды. Таңдамалы жиынтық негізгі жиынтықты толығымен анықтау үшін оның негізгі ережелерін ескеру керек:
- таңдау толығымен тұлғалы болуы керек, яғни, негізгі жиынтық дербес түрлерінің белгілі саны болуы керек;
- таңдау объективті болуы керек, яғни оның құрамына субъективті емес кейдесоқ таңдау принципі бойынша құралған;
- таңдау сапалы біркелкі болуы керек ( тәжірибе бөлінген топтар аналогтар бойынша түрлерге, жасқа, физиологиялық және басқадай факторлар) .
Таңдау көлемдері бойынша аз санды 30 дербестіктен құралған және көп санды боп бөлінеді.
Жеке дербес белгінің сандық мәнін варианттар деп атайды ( лат. Varians) . Тірі жануардың қасиеті мен белгілік өзгеруін вариациялау деп атайды. Белгісіз жүйесіз ( зерттеудегі) бақылаудағы алынған вариант жиынтығын бастапқы ( шикі) қатар ( рет) деп санайды. Варианттарды өсу ретінде орналастыру ( немесе құлдырау, азаю) ранжирлеу деп есептеледі ранжирлі рет, қатар) . Класттарға мәнінен тәуелді, ол вариациялық рет, қатар деп аталады.
Биологиялық белгілер байланысы арасындағы бір белгінің белгілі мәнін басқа белгілердің бірнеше мәндеріне сәйкес келсе, оның вариацияланған орташа мәнін, корреляция деп атайды.
Биологиялық белгілер, егер олар есеп пен шаралар көмегімен, математикалық өрнек мәнін алса; орташа арифметикалық, орташа квадраттық, өзгергіштік коэффициенті, корреляция коэффиценті және басқалар. Белгілер өлшеу нәтижелері, сондай - ақ, олардың вариациялау ерекшеліктері, өзара байланысы мен тұқым қуалауды математикалық әртүрлі символдармен белгіленеді ( 1 кесте)
Кесте 1
Max X
Min V
Max V
Min V
1 кестенің жалғасы


Модальдық класстағы ауытқу
(орташа шарттық)



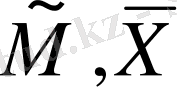
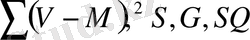
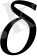
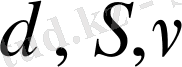
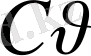
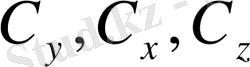
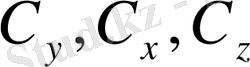
1 кестенің жалғасы
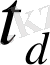
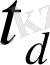
Фишер айқындығының көрсеткіші
(дисперсиялы талдауда)
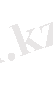
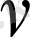
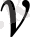
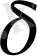
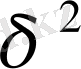
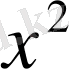
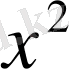
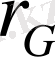
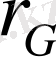
1 кестенің жалғасы
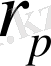
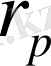
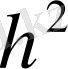
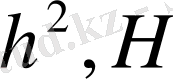

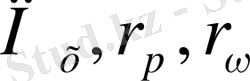
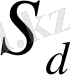
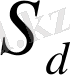
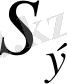
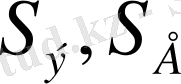
1. 4 Биологиялық белгілер және оларды топтастыру ( жіктеу)
Мал мен оның өміршендік өнімдерін бағалау, сондықтан, статистикалық жиынтықты құрау нақты белгілер бойынша жасалады, олар белгілі ғылыми және практикалық мүдде көрсетіп дербес арасында айырмашылық пен салыстыруға мүмкіншілік етеді.
Өзінің табиғи тұқым қуалауы бойынша және белгілерді бағалау есебінен ол сапаға және санға ( мөлшерге) бөлінеді.
Сапалық белгілер, заң бойынша, көп генді іс - әрекет ( бір генмен), альтернативті сызба бойынша өрнектіліп визуалды бағаланады малдардың түр - түсі, дене бітім типі, өнімдер мен басқалардың дәмі мен иісі) . Осындай белгілерді биометриялық өңдеуде малдардың ранжирлік ретте орын алу көрсететін сан пайдаланады.
Сандық ( мөлшерлік) белгілер - ол ағзаның ерекшілігі мен қасиеті, оның мәні өлшемді және санмен өрнектелді. Өз кезеңінен олар санаулы және өлшемді боп бөлінеді.
Санаулы белгілер санау жолмен ескеріліп дискретті вариацияланады (үзіліспен) . Олардың мәні тек қана толық сандармен өрнектеледі (мы салы, тауықтардың жұмыртқалағыштығы, ана торайлардың көп төлдігі және басқалар) .
Өлшемді белгілер өлшенеді және олардың мәні жобалы өрнектеледі, яғни толық және бөлшек сандармен ( мысалы, сүт өнімділігі, малдың тірі салмағы, т. б. ) .
Мөлшерлі белгілер, заң бойынша, полигонды тұқым қуалау сипатта болып және үзіліссіз өзгереді ( яғни, бір белгі көппен терминияланады, бір қалпыты іс - қимылды гендермен) .
2 Вариацияланатын мәндердің статистикалық талдауы
2. 1 Статистикалық топтасудың негіздері
Өткізілген зерттеулер жөніндегі есеп дайындау процесінде тәжірибелермен сынақтар нәтижелері сәйкестік журналдарға жазылып, белгілі бір талдауға түсіп, статистикалық бақылауға алынады. Ақиқатты табу үшін бақылауған алынған деректерді жүйеге келтіріп, өңдеу қажет.
Бақылдаудан алынған материал нәтижелерін логикалық және арифметикалық бақылауға алады. Логикалық бақылау деректердің мәндік келісімімен бақылауға түседі, ол бастапқы жазуда көрсетіледі (мысалы, сиырдың 18 см тең болып, ол оның сәйкестікке жатпайды) .
Арифметикалық бақылау жекелей жазылғандардың есептік тексеруге сәйкестіріледі. Мысалы, жазуда «Прогресс» оқу шаруашылығында 970 сиыр бар, ал бір ірі қара мал 870 бас. Бөлік толық саннан аспайтындықтан, бұл әрине қателік болып есептеледі.
Зерттеу процесінде жинақталған материал әрбір процестер мен құбылыстарды айқындайтын қызықты деректер береді. Бірақ та, материал бойынша шашылған деректер ештеңе бермейді. Осы процестер мен құбылыстардың айқындалу заңдылығын тек қана белгілі деректерді өңдеуде байқауға болады. Ол топтастырылу арқылы шешіледі.
Бірліктерді топқа қосу әр жеке жағдайда айқындалатын ерекшеліті анықтау мүміндігін береді.
Топтастыру негізіне сол немеес басқадай белгі жатады. Мысалы, сиырлар тобынын сүттілігі бойынша, сүт майлығы бойынша, тірі салмағы бойынша, жасы және т. б. бойынша топтастыруға болады.
Топтастыру процесінде вариациялық рет ( қатарлар) құрылады. Рет (қатар) үш түрлі болады:
Тек қана мөлшерлік өрнекті алатын, белгінің топтасуын көрсететін бөлу қатары ( өнімділік, жас, т. б. ) .
Мәтіндік жазбада тіркелетін белгі сапасы бойынша айқындалатын атрибут қатары :
-түрі, типі, жақындығы (тұқымдық құрамы, жыныстық жас құрылымы, қоректенуі типі және т. б. ) Ондай белгілер санмен емес әріп көмегімен жазылады.
-географиялық қатар территориялық бөліктегі кеңістік топтасуын көрсетеді.
Вариациялық қатар топтасуды кластар бойынша өткізуге мүмкіншілік береді, ол вариация белгілерінің заңдылығын көрсетіп, статистикалық шама қатарын есептейді. Вариация қатарын құру үшін биометриялық шаманы есептерді есептеу техникасының варианттан артық болады.
Вариациялық қатардың мысалы ретінде сиырлар табынын кластарға сүттілігі бойынша бөлу жатады (2 кесте) .
Кесте 2
Σ Р=185
Биометриялық шаманы есептейтін, вариациялық қатарды құру тәртібі және оның талдауы 9. 2. п. келтірілген.
Вариациялық қатардың заңдылығын полигондық бөлу немесе гистограмма ретінде графикалық өрнектеуге болады.
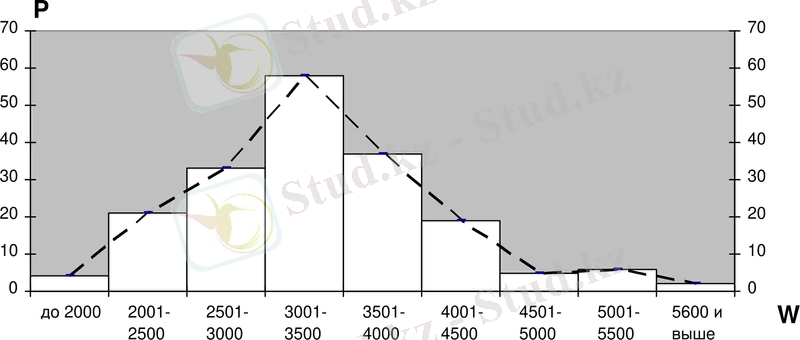
Сурет 1
1 суретте жалпы сызықпен сиырлардың сүттілігі бойынша бөлу гистограммасы көрсетіліп, үзікті сызықпен - бөлу полигоны берілген. Гистограмманың сатылығы мен вариациялық қисықтың сынық түрі (бөлу полигоны) таңдау вариантының аздаған мөлшерімен түсіндіріледі. Егер бақылау саны үлкен болса, вариациялық қисық бағу сипатта болып ол теориялық түрге айналып, бас жиынтықтың мүшелерін бөлуді сипаттап, теориялық мәнді жиілік пен түрі бойынша биноминалды қисықты еске салады
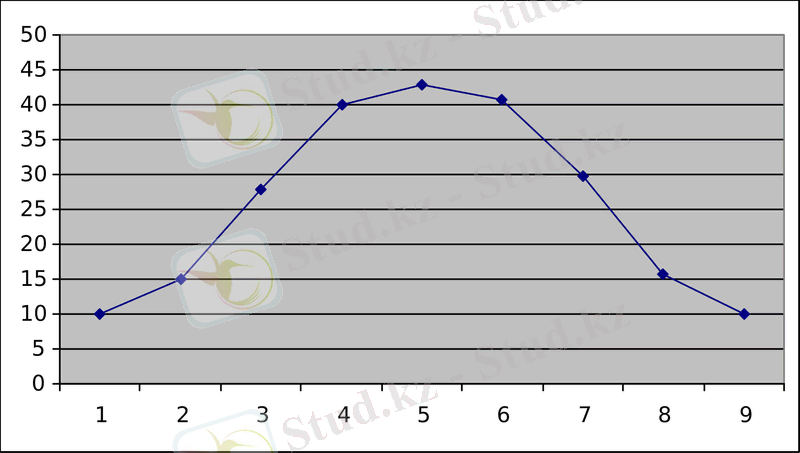
Сурет 2
Сурет 2
Вариациялық қатардың параметрлерін пайдалана, М орташа арифметикалық және орташа квадраттық ауытқуды
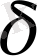 есептеу процесін жеңілдетуге болады.
есептеу процесін жеңілдетуге болады.
2. 2 Орташа шамалар мен оларды есептеу әдістері
Зерттелетін белгінің шамасы бойынша жиынтықты сипаттайтын негізгі көрсеткіш болып орташа арифметика боп саналады. Ол бар белгінің жиын сипаттамасын беріп, типті және тұрақты құбылыстарды көрсетіп, оның құрамын толығымен өрнектейді. Орташа шамада заңдылық өзін толық табады.
Биологиялық статистикада пайдаланатын орташаның бірнеше түрлері бар: орташа арифметикалық, өлшемді орташа арифметиалық, орташа квадраттық, орташа гармониялық, орташа параметрлік емес, мода, медиана және тағы басқалары.
2. 2. 1 Орташа арифметикалықты есептеу М
М- ні вариантты бар мәндерін жиындау жолымен есептейді.
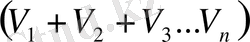 онан соң жиынды варианттар мөлшеріне бөледі:
онан соң жиынды варианттар мөлшеріне бөледі:
 =
=
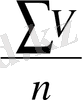
М - орташа арифметикалық
 - жиындау символы
- жиындау символы
V - варианттың сандық мәні
n - таңдау көлемі ( вариант мөлшері)
мысалы, егер сүттілік жекелік 12, 3; 10, 7; 9, 5; 14, 5; 13, 5; 15, 0 кг болса, топтағы алты сиырдың орташа тәуліктік сүттілігін анықтау қажет
 =
=
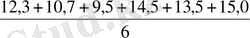 =
=
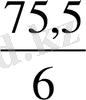 =
=
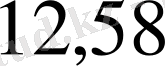 кг
кг
Есеп техникасы барда орташа арифметикалықтың осындай әдісі кез келген санның мөлшерін шығаруға тиімді. Егер, есептегіш машина болмағанда және нақты варианттарды қосу қиынға соқса, онда вариациялық қатарды құру арқылы есептеудің айналма жолын қолданамыз. Мұнда орташаның нақтылығының аздап төмендеу есебінен, есептеу жұмысы біршама жеңілденеді. Есептеудің екі әдісі қолданылады, олар: М - көбейту және жинақтау.
ЭВМ пайдалану есебінен және әр түрлі сандарды таңдау үшін орташа арифметикалық есептеу техникасы 1, 2, 3 алгоритмдерді және
« БОИ» бағдарламасының 0І режимінде көрсетілген.
2. 2. 2 М
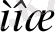 - өлшемді орташаны есептеу
- өлшемді орташаны есептеу
Өлшемді орташа өзімен бірнеше жиынтықты орташа арифметикалықтың орталанған нәтижелерін көрсетіп мына формула бойынша есептеледі
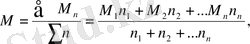 мұнда
мұнда
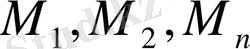 - жеке
- жеке
жиынтықтың орташа арифметикалығы.
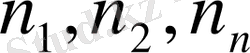 - жиынтықтың көлемдері.
- жиынтықтың көлемдері.
Егер М жое - есептегенде бір топтағы малдар үшін, онда екі белгі еске алынады ( мысалы, лактациядағы сүт майы орташа есебі, мұнда ай сайынғы сүттілік орта майлылығымен еске алынады), мына формуламен жазылады
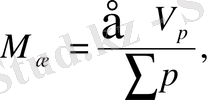
мұнда V - белгінің мәні, Р - белгінің орталанған математикалық салмағы.
Мысалы, лактациядағы 10 ай ішіндегі сиырлардан алынған сүттің орташа майлылығын есептеу 3 кесте деректері бойынша мүмкін.
Кесте 3
Лактация
үшін
3, 7
3, 8
3, 9
3, 9
4, 0
4, 0
4, 1
4, 1
4, 3
4, 4
490
590
520
460
430
410
370
320
290
110
Бір пайызды
сүт Vp
1813
2242
2028
1794
1720
1640
1517
1312
1247
484
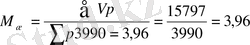 %
%
2. 2. 3 Параметрлік емес орташаны есептеу
Параметрлік емес орташаны ( орташа ранг) анықтау сапалық белгілер үшін қажет, ол өз шамасын анықтағанда сандық өрнексіз болады.
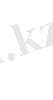
Мысалы, аң шаруашылығында, көгілдір құндызбен айналысатын, екі аталықтан және аналық топтан 12 күшік әр түрлі түсті былғары тері: ( ашық көгілдірден қою көгілдір түс) . Тұқымда қай аталықтан қою көгілдір түсті тері алынғанын анықтау қажет. Ол үшін бар төлдерді ранжирлік ретке қойып, түстің қоюлануына сәйкес, мұнда әр кезектік нөмірге әкесінің нөмірі қойылады:
Ранг ( әлсізден қою - көкке дейін) 1 2 3 4 5 6 7 8 9 І0 І І І2
Тұқым беруші әкесінің нөмірі ІІ І ІІ І І ІІ І ІІ І І ІІ І
Сонан соң әр аталықтың тұқымдағы сүттік орташа рангісін есептейді, былайша
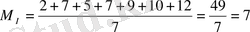 ;
;
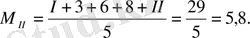
Екі аталықтың тұқымдарының тері түсінің өзгеруін арифметикалық орташамен салыстыра, 1 аталық орташа аса қою түспен тұқым беретінін тұжырымдаймыз.
2. 3 Өзгергіштіктің көрсеткіштерімен оларды есептеу әдістері
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz