Геометриялық ұғымдарды қалыптастыру әдістемесі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

3-Дәріс. Геометриялық ұғымдарды қалыптастыру әдістемесі

Геометриялық ұғымдарды қалыптастыру әдісінің ерекшеліктерін қарастырыңыз (NS тек геометрияның алғашқы сабақтарында) .

Г. Фрейденталь былай деп жазды:" мектепте математика аяқталған ғылым ретінде емес, қызмет түрі ретінде қарастырылуы керек "("Математика педагогикалық міндет ретінде: мұғалімдерге арналған нұсқаулық. - М., 1982. -Б. 1) . Бұл дегеніміз, Математиканы оқыту процесінде мұғалім әртүрлі жағдайларда (математикалық ұғымдарды қалыптастыру, есептерді шешуге үйрету, теоремаларды дәлелдеу кезінде) белсенділік тәсілін қолдануы керек, оның мәні білімнің белсенділік сипаты болып табылады. (Ол математиканың жалпы әдістемесінің бөлімдерінде толығырақ қарастырылады. )

Негізгі мектепте геометриялық ұғымдарды қалыптастыруда осы тәсілді жүзеге асыруды қарастырыңыз.

Мектеп геометрия курсында зерттелген ұғымдар 2 топты құрайды: анықталмаған және анықталған. Геометрия курсында ұсынылған ұғымдардың көпшілігі "жақын тұқым мен түрлер арасындағы айырмашылықтар арқылы"анықталады. Сонымен қатар, геометрияның әртүрлі оқулықтарында кейде бірдей ұғымдардың әртүрлі анықтамалары қолданылады. Мысалы, әртүрлі оқу құралдарындағы параллелограмм келесідей түсіндіріледі:

а) қарама-қарсы жақтары жұп-параллель болатын төртбұрыш;

б) параллель емес жиектері бар екі жолақтың қиылысы;

в) симметрия орталығы бар төртбұрыш және т. б.

Барлық осы анықтамалар әр түрлі дәрежеде көріну мағынасында тең емес. Тұжырымдаманы қалыптастыру процесінде бейнелі компоненттің маңыздылығын ескере отырып, мектеп геометрия оқулығында қиялға анықталған объектілердің суреттерін оңай салуға мүмкіндік беретін осындай анықтамалар қажет екенін атап өткен жөн. Бұл талап тұрғысынан параллелограммның дәстүрлі анықтамасы, қарама-қарсы жақтары параллель параллель болатын төртбұрыш ретінде ең сәтті болып табылады.

Жалпы, геометриялық ұғымдардың қалыптасуы кезеңдер бойынша жүзеге асырылады.

/ кезең. Тұжырымдаманы қалыптастыру процесі, белгілі болғандай, оны енгізу мотивациясымен басталады. Бұл кезеңнің мәні тұжырымдаманы зерттеуге қызығушылық тудырады. Геометриялық ұғымдарды енгізуді ынталандырудың маңызды құралы-жаттығуларды орындау, фигуралардың модельдерін, атап айтқанда дайын үлгіні қарастыру. Мысалдар келтірейік.

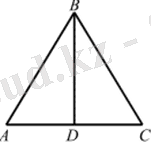
1. Жаттығу орындалады: AAVS-изоссельдер (AB = Vc), BD-в бұрышының биссктрисі (сурет. 3) . A ABD = ACBD екенін дәлелдеңіз.

Оқушылардың назары BD кесіндісі үшбұрыштың жоғарғы жағын қарама-қарсы жақтың ортасымен байланыстыратындығына аударылады. Бұл үшбұрыштың медианасы ұғымын енгізуге мүмкіндік береді.

3-сурет

• 2. Сызық пен шеңбердің өзара орналасуын зерттеу кезінде шеңбер мен сызықтың тек бір ортақ нүктесі болуы мүмкін екендігіне назар аударылады. Бұл жағдай тангенс ұғымын шеңберге енгізуге итермелейді.

• 3. Үшбұрыш, төртбұрыш ұғымдарын осындай нысаны бар заттарды қарастыру негізінде енгізуге болады.

• 4. Әр түрлі фигуралардың модельдерін (текше, пирамида және т. б. ), сондай-ақ айналадағы заттарды қарастырған кезде параллель сызықтар, қиылысатын сызықтар туралы түсініктерді енгізуге болады.

Оқушыларды осы фигураларды салу жаттығуларын орындау барысында көптеген геометриялық фигуралармен таныстыруға болады. Мысалы, изоссельдер үшбұрышы үш жағынан Үшбұрыш салу жаттығуларының нәтижесінде пайда болады, олардың екеуі тең.

Жеке ұғымдарды енгізуге Мотивация геометрия оқулықтарында да қарастырылған. А. в. Погореловтың оқулығында дайын сурет, Л. С. Атанасянның оқулығында және т. б. практикалық тапсырмалар, А. Д. Александровтың оқулығында және т. б. практикалық жағдайлар кеңінен қолданылады.

Материалды зерттеуге ынталандыру теорияны кеңейту немесе тереңдету қажеттілігі болуы мүмкін. Мысалы, векторларды енгізу олармен әртүрлі операцияларды тудырады. Әрбір нақты жағдайда мұғалім тұжырымдаманы енгізуге ынталандыру мәселесін шешеді, ал кейде бұл кезең болмауы мүмкін, мысалы, кіріспе мотивациясы күрделі ұғымдарды немесе студенттер көрнекі идеялар деңгейінде бұрыннан таныс ұғымдарды, сондай-ақ екінші ретті рөл атқаратын ұғымдарды зерттеген кезде.

Және кезең. Оның анықтамасын құрайтын Тұжырымдаманың маңызды қасиеттерін анықтау (студенттердің назарын аудару керек) . Мысалы, тік бұрыштар ұғымының маңызды қасиеттерімен танысу жаттығуды орындау арқылы жүзеге асырылуы мүмкін:

Ашылғаннан өзгеше еркін бұрыш жасаңыз. Оның жақтарын бұрыштың жоғарғы жағынан жалғастырыңыз. Алынған жұп бұрыштарды сипаттаңыз.

Құрылыс нәтижесінде студенттерге белгілі 4 жұп іргелес бұрыштар және екі жұп бұрыштар пайда болады, олардың жақтары қосымша сәулелер болып табылады. Осылайша, осы жаттығуды орындау кезінде студенттер іргелес бұрыштар ұғымын бекітеді және тік бұрыштардың маңызды қасиеттерімен танысады. Белгілі бір қасиеттерді қанағаттандыратын объектілерді салу жаттығуларының көмегімен студенттерді көптеген геометриялық ұғымдармен таныстыруға болады.

5-6 сыныптарда ұғымдардың маңызды қасиеттерін анықтауды фигураларды жобалау жаттығулары арқылы жүзеге асыруға болады, оны студенттер Тұжырымдаманың осы қасиеттерін өздері анықтайды. Мысалы, бұрыш бисекторының маңызды қасиеттерімен танысу қағаз парағын оның жақтары сәйкес келетін етіп бүгу жаттығуларын орындау кезінде жүзеге асырылуы мүмкін.

III кезең. Бұл кезеңде анықталған маңызды қасиеттердің синтезі және Тұжырымдаманың анықтамасы тұжырымдалады.

IV кезең-анықтамадағы әр сөздің түсінігін анықтау. Бұл кезеңде анықтаманы есте сақтауды талап етпеу керек. Оқушыларға анықтамада қолданылатын әр сөздің мағынасы түсінікті ме, жоқ па, соны анықтау керек. Жеке сөздердің мағынасын түсінбеу тұжырымдаманы анықтаудың логикалық құрылымын игеруді қиындатады. Материалды түсіну оны есте сақтаудың маңызды шарты болып табылады.

V кезең-тұжырымдаманы анықтаудың логикалық құрылымын ассимиляциялау. Оған арнайы жаттығулар арқылы қол жеткізіледі. Мұндай жаттығулардың бір түрі тұжырымдамаға жататын объектілерді тану жаттығуларынан тұрады (мұндай жаттығулар қалай жасалады, сіз математиканың жалпы әдістемесі курсында кездестіңіз) .

Геометриялық ұғымдарды қалыптастыру кезінде зерттелген тұжырымдамаға жататын заттарды тануға арналған жаттығулар үшін дайын сызбаларды қолдану ыңғайлы. Мысал келтірейік.

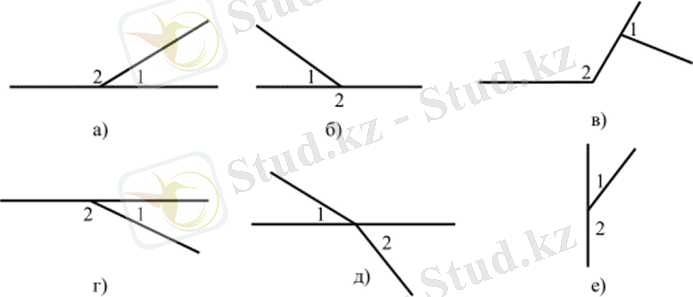
Суретте белгіленген бұрыштардың қайсысы. 4, іргелес ме?

4-сурет

Іргелес бұрыштарды тану кезінде суреттегі әртүрлі кескін жағдайларын қолдану керек. Сіз тану жаттығуларына талаптарды қоса аласыз: көрсетілген объект тұжырымдамаға жататын етіп жағдайды өзгерте аласыз. Дайын сызбалардағы жаттығулардан басқа, белгісіз жауабы бар тапсырмаларды қолдану керек. Мысалы:

2. Егер олардың бір жағы ортақ болса, екі бұрыш іргелес бола ма?

Бұл сұраққа нақты жауап жоқ, өйткені бұл бұрыштардың басқа екі жағы туралы ештеңе айтылмаған.

Тұжырымдаманың анықтамасын ассимиляциялау үшін тану әрекетінен басқа, Нәтижелерді іздеу әрекеті қолданылады. Бұл әрекетті игеру үшін тұжырымдамаға жататын объектінің қасиеттерін табуға арналған жаттығулар ұсынылады. Мысалдар келтірейік.

• 3. Төртбұрыш KPDF параллелограмм. Оның қандай қасиеттері бар?

• 4. 1 және 2 бұрыштары іргелес. Бұдан не шығады?

VI кезең-анықтаманы есте сақтау.

VII кезең-тұжырымдаманы нақты жағдайларда қолдану.

VIII кезең-бұл тұжырымдаманың басқа ұғымдармен байланысын орнату.

VII-VIII кезеңдерде Тұжырымдаманың қасиеттері мен белгілерімен танысу, Осы Тұжырымдаманың басқа ұғымдар жүйесіндегі орнын анықтау жүзеге асырылады. Мұнда студенттер тұжырымдаманы анықтаудан оның әртүрлі маңызды қасиеттеріне және керісінше өту дағдыларын игереді, зерттелген Тұжырымдаманың бұрын зерттелген адамдармен байланысын игереді.

Мектеп геометрия курсында сипаттау арқылы енгізілген бірқатар ұғымдар бар. Бұл ұғымдарды қалыптастыру процесі III және IV кезеңдерді қоспағанда, олардың анықтамаларын көрсете отырып, ұғымдарды қалыптастыру сияқты кезеңдерден тұрады. Мұндай ұғымдарды қалыптастыру бойынша жұмыс мұғалімнің ерекше назарын талап етеді; Тұжырымдаманың қасиеттерін бөліп көрсету, оларды қолдану алгоритмін жасау, маңызды қасиеттер оқушылардың іс-әрекетінің тақырыбы болатын жаттығулар жасау қажет.

Сонымен, геометриялық ұғымдарды қалыптастыру процесі (басқа математикалық ұғымдар сияқты) 8 кезеңнен тұрады. Әр кезеңде жетекші рөл жаттығуларға жатады.

Ұғымдарды қалыптастыру процесі-динамикалық процесс. Оқушылардың тәжірибесіне, ұғымдардың нақты мазмұнына байланысты қалыптасу кезеңдеріне назар аудару әртүрлі болуы мүмкін.

3. Геометрияның алғашқы сабақтарында есептерді шешуге үйрету

Бұл мәселе г. И. Саранцевтің "геометрияны оқыту әдістемесі" оқу құралында толық қамтылған (қазан, 2011) . Оны егжей-тегжейлі қарастырайық.

"Мәселелерді шешудегі сәттілік, - дейді автор, - көбінесе тапсырманың талабы мен жағдайынан ақпарат алу, жеке элементтерді оқшаулау, оларды біріктіру, тапсырманың талабын қайта құру, салдарды шығару, сызбамен жұмыс істеу қабілетімен анықталады. Сондықтан, бұл дағдыларды қалыптастыру математика мұғалімінің ерекше қамқорлығы болуы керек және оны жүйелі және мақсатты түрде жүзеге асыру керек. Курстың бірінші бөлімдерін оқып-үйрену кезінде VII сыныптағы геометрияның алғашқы сабақтарында бұған ерекше назар аудару керек, өйткені келесі бөлімдердің материалдарын сәтті игеру оқушылардың осы дағдыларды игеруін қамтиды" [5, 511-бет.

Дағдыларды қалыптастыру жаттығуларды орындау барысында белгілі болады. Оқушылар жоғарыда аталған әрекеттерді игерудегі алғашқы дағдыларды келесі жаттығуларды орындау кезінде алады.

I топ 1. Бұл түзу сызықта жатпайтын түзу және үш л, В, С нүктелері берілген. LV кесіндісі түзу сызықты кесіп өтетіні белгілі. Қандай жағдайда ӘК кесіндісі осы түзу сызықты кесіп өтеді?

Жауап нұсқаларының бірі: AC сегменті бұл сызықты кесіп өтпейді.

2. Кесіндінің ұштары а түзу жазықтығын бөлетін әртүрлі жарты жазықтықтарға жатады деп айту үшін не білу керек?

Жауап. АВ кесіндісі а сызығымен қиылысады.

3. А в сәулесінде АС кесіндісі кейінге қалдырылған. С нүктесі А және В нүктелерінің арасында жатыр деп айту үшін қандай шарт қосу керек?

Жауап. АС кесіндісі АВ кесіндісінен кіші.

4. А, В, С нүктелері бір түзу сызықта жатыр. А және В нүктелері арасында С нүктесі қандай жағдайда болады?

Жауап. А в кесіндісінің ұзындығы АС және ӘК кесінділері ұзындықтарының қосындысына тең, не АВ кесіндісі АС кесіндісінен үлкен және АВ және АС кесінділері оның басынан бастап бір сәуледе л.

• 5. АВС үшбұрышының АВ жағында D нүктесі алынады, AO = 5 см екендігі белгілі, шартты АВ үшбұрышының бүйірін табуға болатындай етіп толықтырыңыз.

• 6. АВС, PQR және XYZ үшбұрыштары тең. АВ = 5 см, QR = 6 см екендігі белгілі. әр үшбұрыштың қалған жақтарын табу үшін тағы не білу керек.

Бұл жаттығулармен жұмыс істеу әдісі қандай? Олар студенттерге тиісті фактілерді оқу кезінде ұсынылуы мүмкін. Мысалы, 3 - жаттығу сегменттердің орналасуының негізгі қасиеттерін зерттегенде, ал 6 - жаттығу үшбұрыштардың теңдігін зерттегенде. Негізінен ұсынылған жаттығуларды ауызша орындауға болады. Олардың мақсатына баса назар аударылады. Мысал ретінде 3 жаттығуымен жұмыс істеу әдістемесін қарастырыңыз.

Тапсырманың мазмұнын талдау кезеңі жағдайды, тұжырымды, сызбаны нақтылауды қамтиды. Әрі қарай оқушылармен әңгіме осындай болуы мүмкін.

Мұғалім. Сонымен, біз AC кесіндісі AB сәулесіне қойылғанын білеміз. А, В және С нүктелері қалай орналасқан?

Оқушылар. С нүктесі А және В нүктелерінің арасында немесе В нүктесі Aw с нүктелерінің арасында орналасқан.

Мұғалім. Ал біз не орнатуымыз керек?

Оқушылар. Деректермен бірге "С нүктесі А және В нүктелерінің арасында жатыр"деген қорытынды жасауға мүмкіндік беретін шартты табу керек

Мұғалім. С нүктесі AwBP нүктелерінің арасында жатыр деп айту үшін тағы не білу керек.

Оқушылар. АС кесіндісі а в кесіндісінен кіші.

Мұғалім. Шартқа қандай мәлімдеме енгізу керек?

Оқушылар. АС < АВ.

Аяқталған жаттығудың дизайны осындай болуы мүмкін.

С нүктесі AW в нүктелерінің арасында орналасқан, егер АС кесіндісі АВ және ас<АВ сәулесіне кейінге қалдырылса.

Толығырақ жазбаны пайдалануға болады.

АС кесіндісі АВ сәулесіне қойылғандықтан, онда не С А және В арасында, Не А және С арасында жатыр, егер ас <АВ болса, С нүктесі А және В арасында жатыр.

Мәселенің шешімін іздеуде оның талаптарын қайта құру әдісі үлкен рөл атқарады. Бұл техниканың мәні-бастапқы талап одан туындайтын етіп тапсырма талабын жаңасына ауыстыру. Оқулықтың тиісті бөлімдерін оқу кезінде оқушылар орындайтын келесі жаттығулар осы техниканы игеруге бағытталған.

II топ 7. Мәселелерді алдын-ала олардың талаптарын бастапқы талаптар туындайтын етіп жаңаларына ауыстыру арқылы шешіңіз.

7. 1. Тік бұрыштардың бисекторлары бір түзу сызықта орналасқанын дәлелдеңіз.

Шешімге нұсқау. Тік бұрыштардың бисекторлары арасындағы бұрыш кеңейтілгенін дәлелдеңіз.

7. 2. AB және CD сегменттері O нүктесінде қиылысады, Егер A C, SV, BD және AD сегменттері тең болса, онда AB және CD түзулері перпендикуляр болатындығын дәлелдеңіз.

Шешімге нұсқау. АВ сәулесі CAD бұрышының биссектрисасы, ал CD сәулесі - ACV бұрышының биссектрисасы екенін дәлелдеңіз.

7. 3. АВ және CD-нің екі сегменті О нүктесінде қиылысады, бұл олардың әрқайсысының ортасы. ACD және Vos үшбұрыштарының теңдігін дәлелдеңіз.

Шешімге нұсқау. As = BD және SV = AD екенін дәлелдеңіз.

7. 4. Әрқайсысы екіншісінің ортасынан өтетін екі шеңбер құрыңыз. Бұл шеңберлерде қанша ортақ нүкте бар?

Шешімге нұсқау. Әрқайсысы екіншісінің ортасынан өтетін шеңберлердің қиылысу нүктелерін табыңыз.

7. 5. Егер о және 02 орталықтары бар екі шеңбер сыртқы түрде М нүктесінде бір-біріне тиіп кетсе, онда 0М + М0 ₂ = 0 ₂ . Мұны дәлелдеңіз.

Шешімге нұсқау . Oh 0 ₂ және M нүктелері бір сызыққа жататынын дәлелдеңіз.

Біз жаттығулардың екінші тобымен жұмыс істеу әдістемесін 7. 1 мысалында суреттейміз. Тапсырманың шарттары мен талаптарын, сызбаны анықтағаннан кейін, оқушылардың назарын тапсырманың талабын жаңасына ауыстыруға аудару керек, сонда ол бастапқы болады.

Мұғалім. Тік бұрыштардың бисекторлары бір түзу сызықта орналасқандығы қайдан пайда болады? Тапсырма талабын қандай сөйлеммен ауыстыруға болады?

Оқушылар. Тік бұрыштардың бисекторлары арасындағы бұрыш ашылғанын дәлелдеңіз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.