Көп айнымалылардың функциялық тәуелділігі. Евклидтік өлшемді кеңістік

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

2. Көп айнымалылардың функциялық тәуелділігі. Евклидтік өлшемді кеңістік.

Табиғатта, практикада бір шаманың бір-біріне тәуелсіз басқа екі айнымалының өзгеруінен тәуелді болып келетіні жиі кездеседі. Мысалы, тік төртбұрыштың ауданы z оның қабырғалары x пен y-тің өзгерісіне тәуелді, дәлірек айтқанда z=x*y. Бұл жерде айнымалы z-пен басқа екі айнымалы x және y-тің арасындағы функиялық тәуелділікпен кездесіп отырмыз.

Егер жазықтықта орналасқан екі нүкте $M_{1}\left( x_{1}{, y}_{1} \right),$ $\ M_{2}\left( x_{2}{, y}_{2} \right)$ берілсе, онда ол нүктелердің арақашықтығы 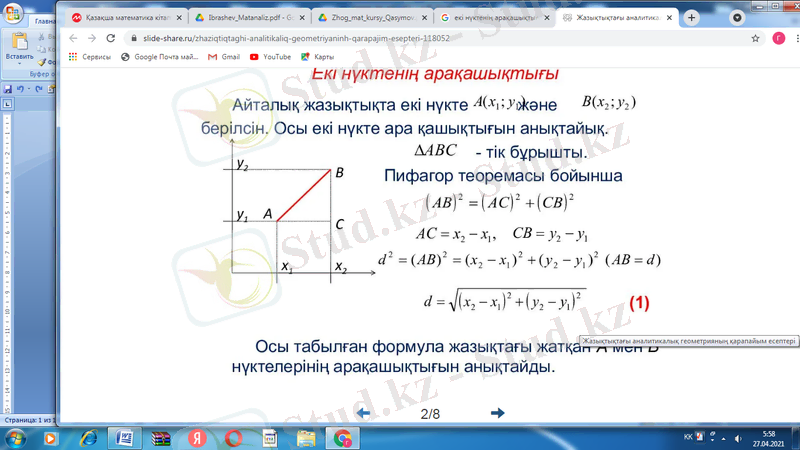формуласымен анықталады. Мұндағы айнымалы шама d басқа $\left( x_{1}{, x_{2}, \ y}_{1}{, y}_{2} \right)$ төрт айнымалылардың (берілген нүктелердің координаталарының) өзгерісіне тәуелді.

Бір айнымалының өзгерісі басқа екі, үш, төрт, одан да көп айнымалылардың өзгерісіне тәуелді болатынына көзіміз жетті. Міне осындай тәуелділікті бір айнымалылардың көп айнымалыларға функциялық тәуелділігі деп атаймыз.

Егер m өлшемді кеңістік беріліп, оның А( $a_{1}, \ a_{2}, \ldots, \ a_{m})$ мен В( $в_{1}, \ в_{2}, \ldots, \ в_{m})$ екі нүктесінің ара қашықтығы 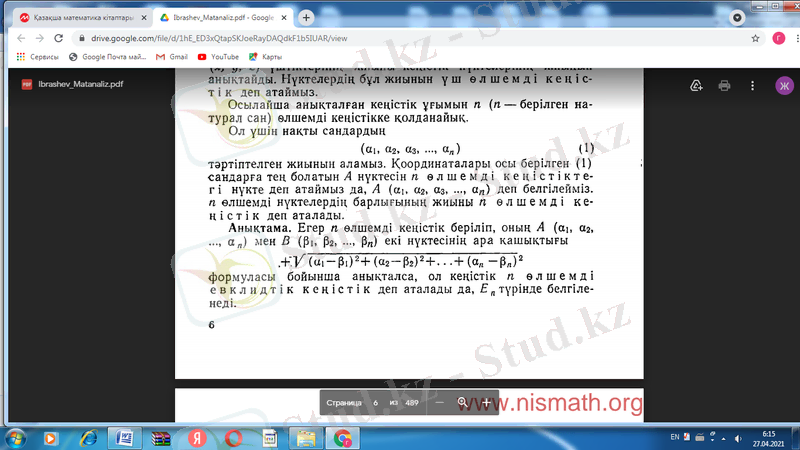формуласы бойынша анықталса, ол кеңістік m өлшемді евклидтік кеңістік деп аталады да, $E_{n}$ деп белгіленеді. A және В нүктелерінің ара қашықтығы p(A, В) деп белгілеу қабылданған. Демек, m өлшемді евклидтік кеңістікте мына формула орындалады:

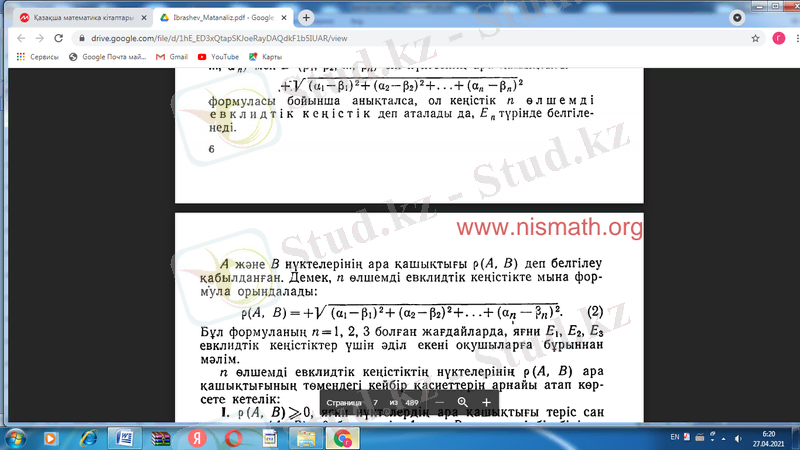
m өлшемді евклидтік кеңістіктің нүктелерінің p(A, В) ара қашықтығының төмендегі кейбір қасиеттері:

1) p(A, В) $\geq 0$ , яғни нүктелердің ара қашықтығы теріс сан емес, ал p(A, В) =0 болу үшін А мен В нүктелері бір-бірімен беттесуі қажет және жеткілікті.

2) p(A, В) = p(В, А), яғни екі нүктенің ара қашықтығы оны А-дан бастап В-ге дейін немесе керісінше, өлшеуден тәуелді емес.

3) Егер $E_{n}$ евклидтік кеңістігіндегі кез келген үшінші бір С( $с_{1}, \ с_{2}, \ldots, \ с_{m})$ нүктесін алсақ, онда үшбұрыштар теңсіздігі деп аталып кеткен мына теңсіздік орындалады: p(A, C) $\leq$ p(А, В) + p(В, С)

3. Көп айнымалылар функциясының анықтамасы және бар болу облысы. Ашық және жабық жиындар.

Егер заң немесе ереже бойынша x пен y аргумент мәндерінің әрбір қос мәніне айнымалы z шамасының бір мәні сәйкес қойылса, айнымалы z екі аргументтің функциясы деп аталады және бұл функция былай белгіленеді:z=f(x, y)

Егер аргументтер x пен y-тің нақты мәндерінен құрылған $\left\{ М \right\}$ жиынының құрамындағы әрбір(x, y) -ке сәйкес белгілі бір заң немесе ереже бойынша, сол аргументтердің функциясы z толық анықталған бір нақты мән қабылдаса, М жиыны екі аргументтің функциясы z-тің бар болу облысы деп аталады.

Егер M жиынының барлық шекаралық нүктелері сол жиынның құрамына енген болса, ондай жиын жабық жиын деп аталады.

Егер жазықтықтағы нүктелерден тұратын L жиынының

1) кез келген нүктесі жиынның ішкі нүктесі болса,

2) L жиынының кез келген екі нүктесін бүтіндей сол жиынның ішінде жатқан үзіліссіз қисықпен қосу мүмкін болса, L ашық жиын деп аталады.

Ашық жиынның анықтамасындағы екінші шарт орындалса, жазықтықтағы нүктелердің бұл жиыны байланысқан жиын деп аталады.

Егер жазықтықтағы нүктелерден тұратын N жиынының құрамындағы A $\in$ N $\$ нүктесі өзінің қандайда болса бір $\delta$ маңайымен бірге сол N жиынының ішінде жатса, A $\$ нүктесі N жиынының ішкі нүктесі деп аталады.

Егер жазықтықтағы нүктелерден тұратын M жиынының құрамындағы болуы да, болмауы да мүмкін В нүктесінің $\delta$ маңайында, М жиынының нүктелерімен бірге, ол жиынның құрамында жоқ нүктелер деп жатса, В нүктесі М жиынының шекаралық нүктесі деп аталады. M жиынының шекаралық нүктелерінің жинағы сол жиынның шекарасын құрайды.

5. Көп аргументті функцияның үзіліссіздігі. Көп аргументті функцияның үзіліссіздігінің анықтамасы.

z= f(x, y) =f(Р) функциясы $P_{0}(x_{0}, y_{0})$ нүктесінде үзіліссіз деп аталады, егер:

1) z=f(Р) функциясы $P_{0}$ нүктесінде және оның қандай да бір аймағында анықталған

2) $\ P \rightarrow P_{0}$ ұмтылғанда z= f(x, y) функциясының шегі бар болу керек

3) Осы шектің мәні функцияның осы нүктедегі мәніне тең болу керек: $\lim_{P \rightarrow P_{0}\ }{f(Р) } = f(P_{0}) \$

4. Көп аргументті функцияның шегі.

Коши бойынша $\mathbf{(\varepsilon}$ - тілінде) . Егер кез келген $\varepsilon > 0$ санына $\delta > 0$ саны табылып, 0<p(A, $A_{0}$ ) < $\ \delta$ теңсіздікті қанағаттандыратын функцияның анықталу жиынындағы кез келген A нүкте үшін $\left f(A) - b \right$ < $\ \delta$ теңсіздігі орындалса, онда b саны u= $\ f(A)$ функциясының $A_{0}$ нүктедегі шегі деп аталады.

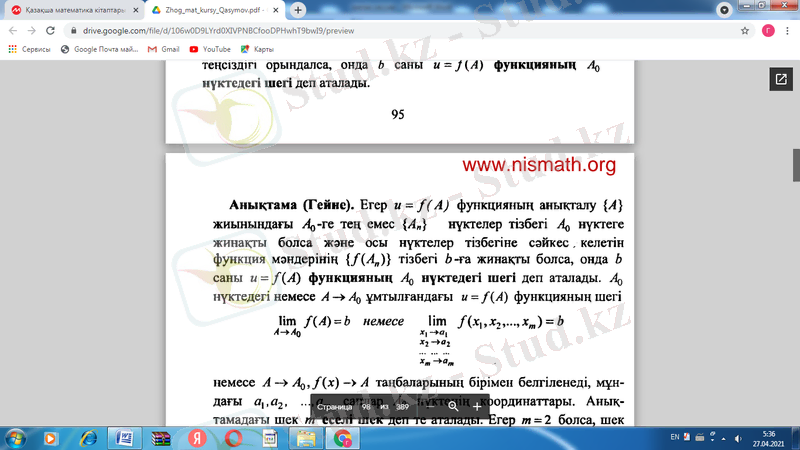
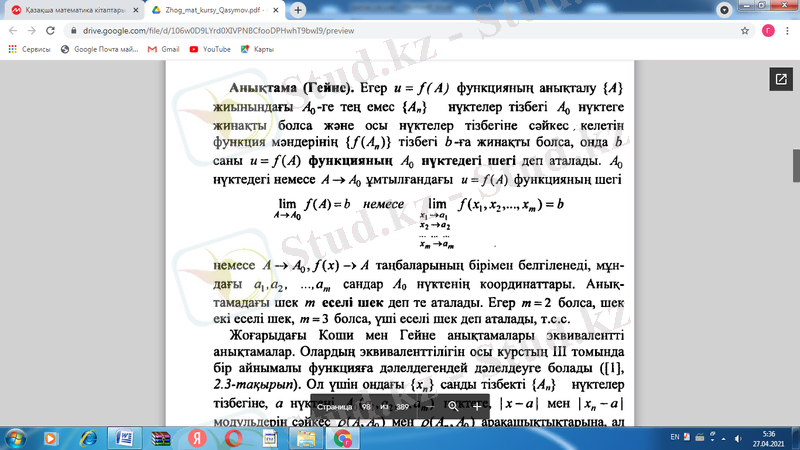
Гейне бойынша (тізбек тілінде) . Егер u= $\ f(A)$ функцияның анықталу $\left\{ A \right\}$ жиынындағы $A_{0}$ -ге тең емес $\left\{ A_{n} \right\}\$ нүктелер тізбегі $A_{0}\$ нүктеге жинақты болса және осы нүктелер тізбегіне сәйкес келетін функция мәндерінің $\left\{ f\left( A_{n} \right) \ \right\}$ тізбегі b-ға жинақты болса, онда b саны u= $\ f(A)$ функциясының $A_{0}$ нүктедегі шегі деп аталады. $A_{0}$ нүктедегі немесе A $\rightarrow$ $A_{0}$ ұмтылғандағы u= $\ f(A)$ функциясының шегі $A_{0}$ ( $a_{1}, \ a_{2}, \ldots, \ a_{m})$

6. Көп аргументті функцияның үзіліс ұғымы.

Егер z=f(Р) функциясы $P_{0}$ нүктесінде үзіліссіз болмаса, онда осы нүктеде функция үзіледі(үзілісті болады), $P_{0}$ нүктесі - үзіліс нүктесі деп аталады.

7. Көп аргументті үзіліссіз функциялардың қасиеттері.

Екі айнымалы функцияларының үзіліссіздігінің қасиеттері(компактылы облыста) :

Компактылы облыс деп тұйық, шектелген аймақты айтады.

1) z=f(x, y) функциясы компактылы аймақта үзіліссіз болса, онда осы аймақта функция шектелген болады.

2) Компактылы аймақта үзіліссіз болатын z=f(x, y) осы аймақта өзінің ең үлкен және ең кіші мәндерін қабылдайды.

3) z=f(Р) функциясы қандайда бір G аймақта үзіліссіз болсын, онда осы аймақтың $P_{1}$ және $P_{2}$ нүктелерін алмасақ та f( $P_{1}$ ) және f( $P_{2}$ ) аралығында орналасқан кез келген C сан үшін G облысына тиісті болатын $P_{0} \in G$ табылады. f( $P_{1}$ ) =C (аралық мән теоремасы деп аталады)

Дербес жағдайда, егер f( $P_{1}$ ) <0, f( $P_{1}$ ) >0 онда G аймағының функцияның мәні 0-ге тең болатындай нүктесі табылады.

Жалпы жағдайда 3-қасиет орындалады.

8. Көп аргументті функциялардың туындылары мен дифференциалдары.

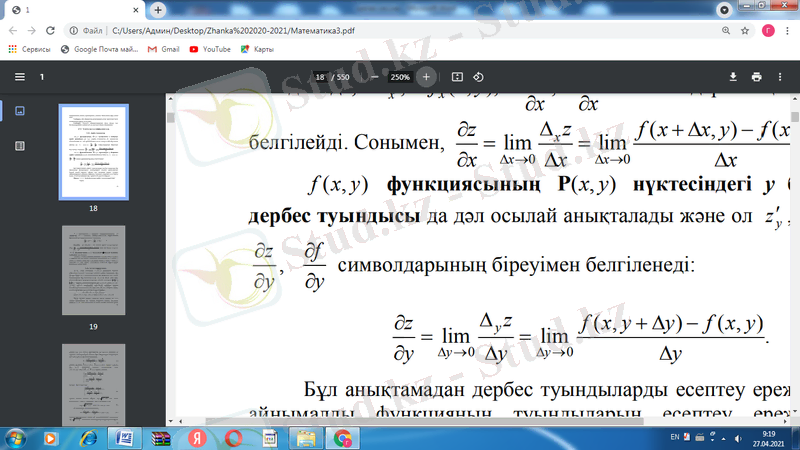
z=f(x, y) функциясының Р(x, y) нүктесіндегі х бойынша дербес туындысы деп $\mathrm{\Delta}_{x}z$ дербес өсімшесінің $\mathrm{\Delta}х$ өсімшесіне қатынасының $\mathrm{\Delta}х \rightarrow 0$ ұмтылғандағы шегін (егер ол шек бар болса) айтады да, 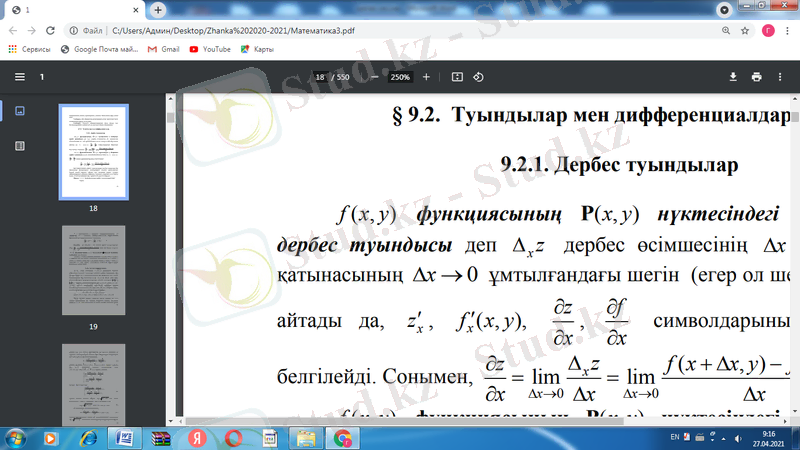символдарының біреуімен белгілейді. Сонымен

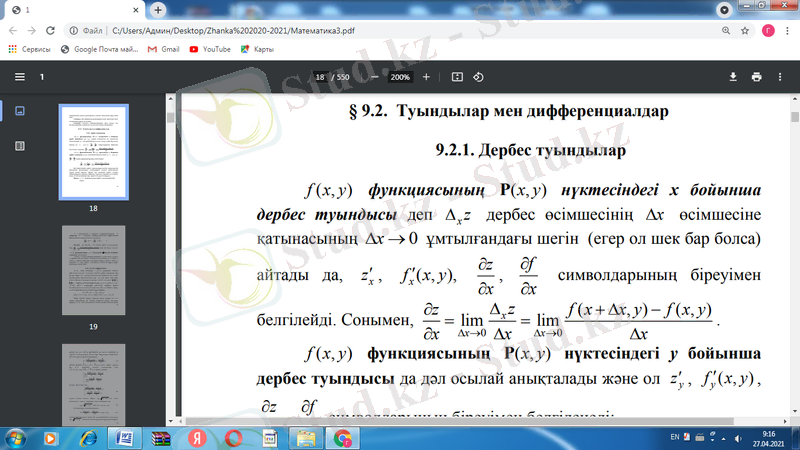
z=f(x, y) функциясының Р(x, y) нүктесіндегі у бойынша дербес туындысы да дәл осылай анықталады және ол

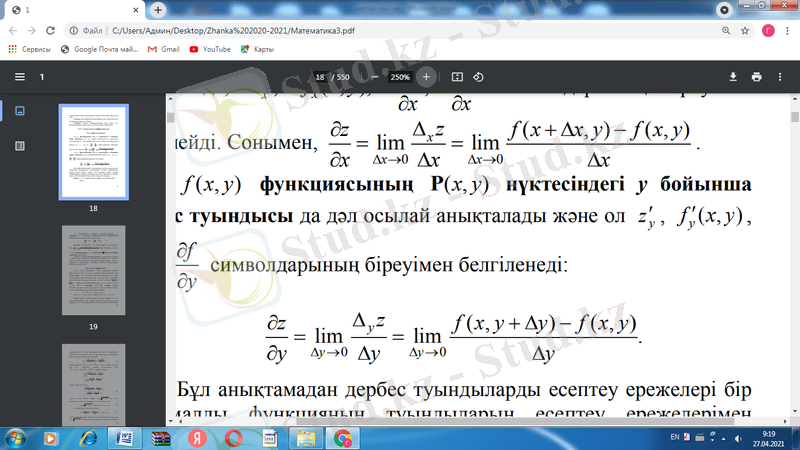
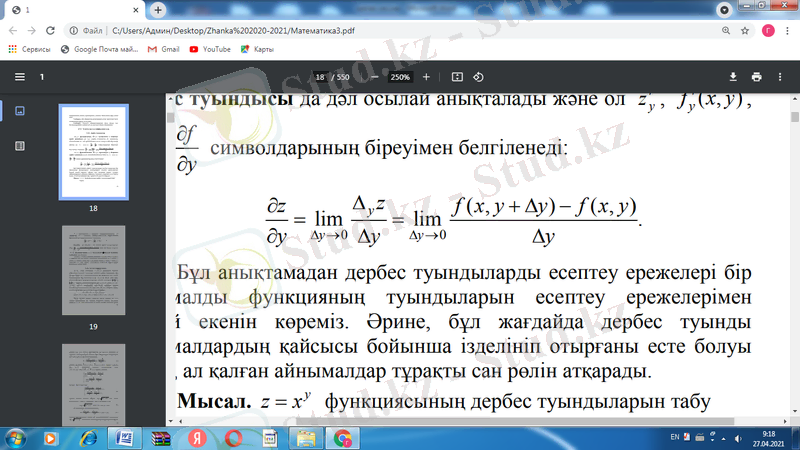
Бұл анықтамадан дербес туындыларды есептеу ережелері бір айнымалды функцияның тундыларын есептеу ережелерімен бірдей екенін көреміз. Әрине, бұл жағдайда дербес туынды айнымалылардың қайсысы бойынша ізделініп отырғаны есте болуы керек, ал қалған айнымалылар тұрақты сан рөлін атқарады.

Берілген z=f(x, y) функциясының кез келген бір айнымалысы бойынша нүктедегі дербес туындысы мен сол айнымалының өсімшесінің көбейтіндісі функцияның дербес дифференциалы деп аталады. x және у айнымалы шамаларының дифференциалдары олардың өсімшелеріне тең, яғни dx= $\mathrm{\Delta}x$ dy= $\mathrm{\Delta}y$

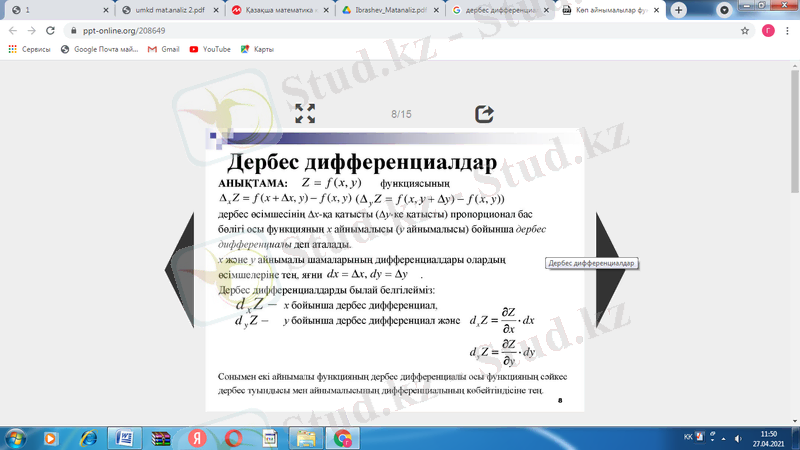
9. Дербес туындылар мен дербес дифференциалдар.

z=f(x, y) функциясының Р(x, y) нүктесіндегі у бойынша дербес туындысы да дәл осылай анықталады және ол

12. Толық дифференциалдың жуықтап есептеуде қолданылуы.

(x, y) нүктесіндегі дифференциалданатын z=f(x, y) функцияның және $\ F_{x}'($ x, y), $F_{y}'($ x, y) дербес туындыларының мәндері белгілі болсын. ( $x + \mathrm{\Delta}x, \ y + \mathrm{\Delta}y$ ) нүктесінде функцияның мәнін есептейік:

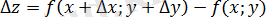
$\mathrm{\Delta}z$ -ті dz толық дифференциалмен алмастырамыз да жуық мәнді табамыз:

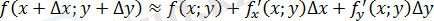
10. Толық өсімше, толық дифференциал және көп аргумент функцияларының дифференциалдануының шарты.

Егер x пен y аргументтеріне сәйкес $\mathrm{\Delta}x$ және $\mathrm{\Delta}y$ өсімшелерін берсек, онда z үшін жаңа $\mathrm{\Delta}z$ өсімшесін аламыз. Ол z функцияның толық өсімшесі деп аталады:

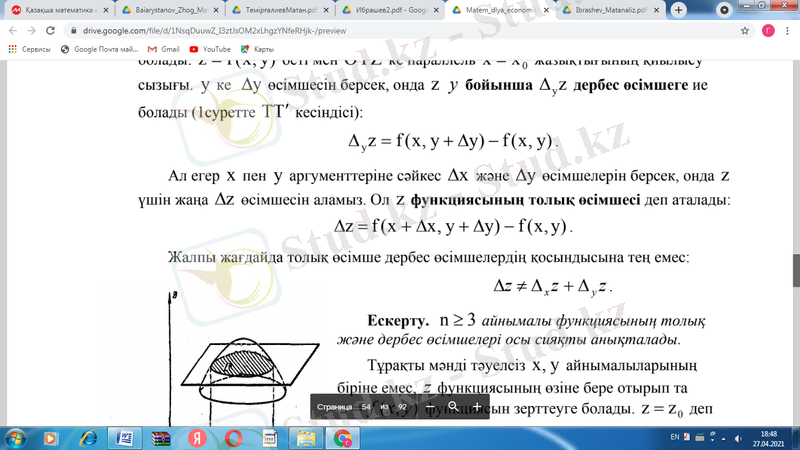
z=f(x, y) функцияның үзіліссіз болуы үшін $Р_{0}\left( x_{0}{, y}_{0} \right) \$ нүктесінде $\mathrm{\Delta}z$ толық өсімшесі $\mathrm{\Delta}x$ , $\mathrm{\Delta}y$ өсімшелерінің нөлге ұмтылғандағы шегі нөлге тең болуы қажетті және жеткілікті. $\underset{{\mathrm{\Delta}x \rightarrow 0}{\mathrm{\Delta}y \rightarrow 0}}{\ \ \ \ \ \ lim}{\mathrm{\Delta}z = 0}$

z=f(x, y) функциясының толық дифференциалы $\mathrm{\Delta}x$ пен $\mathrm{\Delta}y$ -ке қатысты сызықтық болатын және функция өсімшесінен 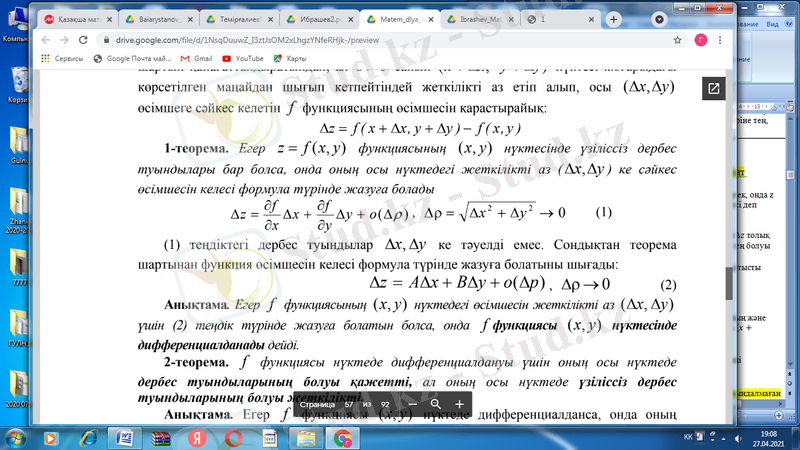-ға қарағанда жоғары ретті ақырсыз кіші функцияға ғана айырмашылығы болатын өрнекті айтады.

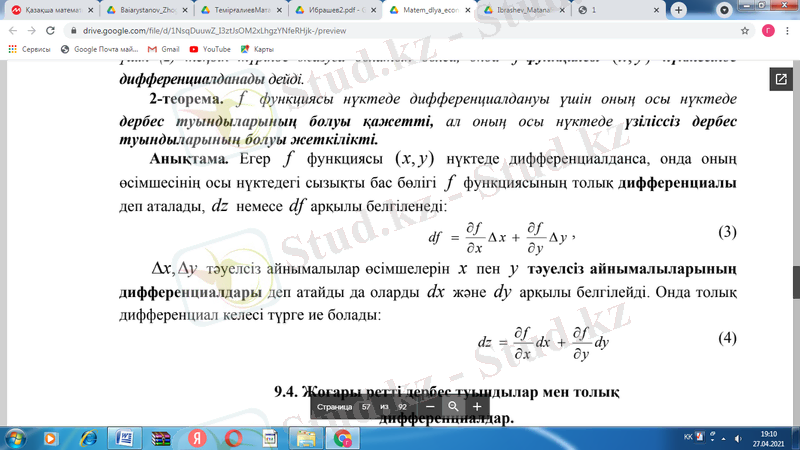
Егер z=f(x, y) функциясы х, у нүктеде дифференциалданса, онда оның өсімшесінің осы нүктедегі сызықты бас бөлігі z=f(x, y) функциясы толық дифференциалы деп аталады.

$\mathrm{\Delta}x$ , $\mathrm{\Delta}y$ тәуелсіз айнымалылар өсімшелерін х пен у тәуелсіз айнымалыларының дифференциалдары деп атайды да оларды dx және dy арқылы белгілейді. Онда толық дифференциал келесі түрге ие болады:

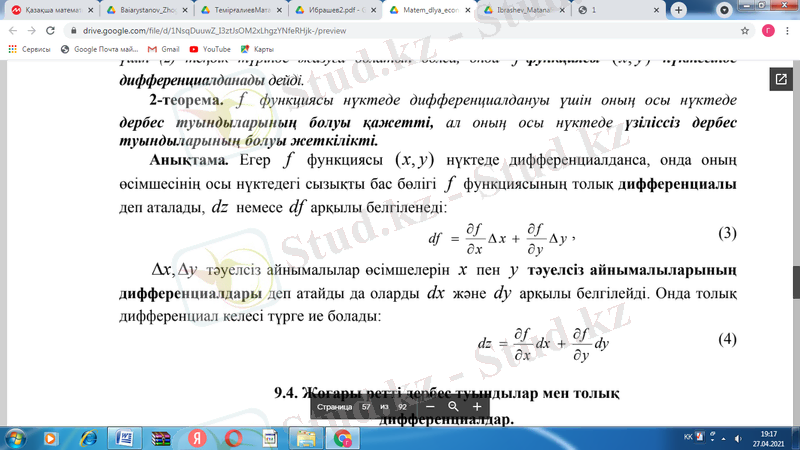
Көп аргумент функцияларының дифференциалдануының шарты: z=f(x, y) функциясы дифференциалдану үшін оның осы нүктеде дербес туындыларының болуы қажетті, ал үзіліссіз дербес туындыларының бар болуы жеткілікті.

42. Дәрежелік қатардың жинақталу радиусы туралы Коши-Адамар теоремасы.

$R$ санын жинақталу радиусы дейді, яғни барлық $x$ үшін $x < R$ болғанда қатар абсолютті жинақталатын, ал $x > R$ болғанда қатар жинақталмайтын $R > 0$ санын айтады.

$\ R = \frac{1}{\lim_{n \rightarrow \infty}\sqrt[n] {\left a_{n} \right}}\ \ \ \$

11. Көп аргументті күрделі функцияларды дифференциалдау.

1) Дифференциалданатын z=f(x, y) функциясы берілсін, мұнда $x = \varphi(t), \ y = \psi(t)$ яғни z=f [( $\varphi(t), \psi(t)$ ] функциясының $t$ бойынша туындысы мына формула бойынша анықталады:

$\frac{dz}{dt} = \frac{\partial z}{\partial x}\frac{dx}{dt} + \frac{\partial z}{\partial y}\frac{dy}{dt}$

2) Дифференциалданатын z=f(x, y) функциясы берілсін, мұнда $\ y = \psi(x)$ яғни z=f [ $x, \psi(t)$ ] функциясының $x$ бойынша туындысы мына формула бойынша анықталады:

$\frac{dz}{dx} = \frac{\partial z}{\partial x} + \frac{\partial z}{\partial y}\frac{dy}{dx}$

3) Дифференциалданатын z=f(x, y) функциясы берілсін, мұнда $x = \varphi(u, v), \ y = \psi(u, v)$ яғни z=f [( $\varphi(u, v), \psi(u, v)$ ] функциясының $u$ және $v$ бойынша туындысы мына формула бойынша анықталады:

$\frac{dz}{du} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial u}$

$\frac{dz}{dv} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial v} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial v}$

17. Тейлор формуласы.

z=f(x, y) функцияcы беріліп, $A_{0}\left( x_{0}{, y}_{0} \right)$ мен $A_{1}\left( x_{0} + \mathrm{\Delta}x{, y}_{0} + \mathrm{\Delta}y \right)$ ( $\mathrm{\Delta}x, \ \mathrm{\Delta}y$ аргумент өсімшелері) нүктелерін қосатын кесінді $A_{0}\left( x_{0}{, y}_{0} \right)$ нүктесінің маңайынан шықпайтын болсын.

Теорема. Егер f(x, y) функцияcы $A_{0}\left( x_{0}{, y}_{0} \right)$ нүктесінің маңайында $n + 1$ рет туындыланып, дербес туындылардың барлығы да үзіліссіз болса, ол функцияның толық өсімшесі үшін мына теңдік орындалады:

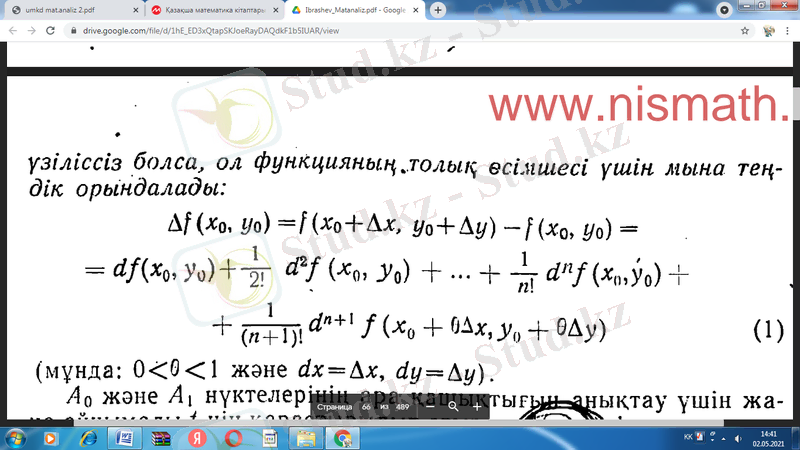
13. Көп аргумент функцияларының жоғары ретті туындылары мен дифференциалдары.

Жоғарғы ретті туындылар. z=f(M) функцияcы M(x, y) нүктесінің кейбір маңайында анықталған және осы маңайдың әрбір нүктесінде $\ f_{x}'(x, y$ ) және $\ f_{y}'(x, y$ ) дербес туындылары бар болсын. Бұл жағдайда дербес туындылар M нүктесінің осы маңайында $x$ және $y$ айнымалылардың функциясы болады. Бұларды бірінші ретті дербес туындылар деп атайды және белгіленуі

$z_{x\ }' = \frac{\partial z}{\partial x}, {\ z}_{y}' = \ \frac{\partial z}{\partial y}$

$z_{x\ }' = f_{x}'(x, y)$ және $z_{y\ }' = f_{y}'(x, y)$ функциялардың M(x, y) нүктесінде $x$ және $y$ айнымалылар бойынша дербес туындылары бар болса, оларды f(M) функцияcының осы нүктедегі екінші ретті дербес туындылары деп атайды және белгіленуі

${(z}_{x\ }') _{x}' = z_{xx\ }^{''} = {z_{x^{2}\ }^{''} = f}_{xx}^{''}(x, y) = \frac{\partial^{2}z}{\partial x^{2}}$

${(z}_{y\ }') _{y}' = z_{yy\ }^{''} = {z_{y^{2}\ }^{''} = f}_{yy}^{''}(x, y) = \frac{\partial^{2}z}{\partial y^{2}}$

${(z}_{x\ }') _{y}' = z_{xy\ }^{''} = f_{xy}^{''}(x, y) = \frac{\partial^{2}z}{\partial x\partial y}$ және ${(z}_{y\ }') _{x}' = z_{yx\ }^{''} = f_{yx}^{''}(x, y) = \frac{\partial^{2}z}{\partial y\partial x}$ -аралас екінші ретті дербес туындылары.

Екінші ретті дербес туындылардан $x$ және $y$ айнымалылар бойынша алынған дербес туындылар үшінші ретті дербес туындылары деп атайды және белгіленуі:

${(z}_{xx\ }^{''}) _{x}' = z_{xxx\ }^{'''} = \frac{\partial^{3}z}{\partial x^{3}}$ ${(z}_{yy\ }^{''}) _{y}' = z_{yyy\ }^{'''} = \frac{\partial^{3}z}{\partial y^{3}}$

${(z}_{xx\ }^{''}) _{y}' = \frac{\partial^{3}z}{\partial x^{2}\partial y}$ ; ${(z}_{yy\ }^{''}) _{x}' = \frac{\partial^{3}z}{\partial x\partial y\partial x}$ ; ${(z}_{yx\ }^{''}) _{x}' = \frac{\partial^{3}z}{\partial y\partial x^{2}} {(z}_{xy\ }^{''}) _{y}' = \frac{\partial^{3}z}{\partial x\partial y^{2}}$ ; ${(z}_{yx\ }^{''}) _{y}' = \frac{\partial^{3}z}{\partial y\partial x\partial y}$ ; ${(z}_{yy\ }^{''}) _{x}' = \frac{\partial^{3}z}{\partial y^{2}\partial x}$ -аралас екінші ретті дербес туындылары.

$f_{xy}^{''}(x, y)$ және $f_{yx}^{''}(x, y)$ туындылары аралас деп аталады, оның біріншісі алдымен $x$ , содан соң $y$ бойынша, ал екіншісі, керісінше, алдымен $y$ , содан соң $x\$ бойынша дифференциалдау арқылы алынған.

Теорема . z=f(x, y) функцияcы және оның дербес туындылары $P_{0}\left( x_{0}{, y}_{0} \right)$ нүктесінің белгілі бір маңайында анықталсын. Егер $\frac{\partial^{2}z}{\partial x\partial y}$ және $\frac{\partial^{2}z}{\partial y\partial x}$ аралас туындылары $P_{0}$ нүктесінде үзіліссіз болса, онда $\frac{\partial^{2}z}{\partial x\partial y} = \frac{\partial^{2}z}{\partial y\partial x}$ .