Орта мектепте арифметикалық прогрессияны оқытуға арналған компьютерлік құрал: PowerPoint презентациясы және Turbo Pascal бағдарламасы


І. Кіріспе
Есептеу техникасының өте жылдам дамып, оны ғылымның кез-келген салаларында қолдануға байланысты өмір талабы оқыту процесін жан-жақты және жүйелі түрде компьютерлендіруге әкеліп отыр.
Мемлекеттік білім беру стандартында жазылған ережеде: информатиканы оқытудың практикалық мақсаты оқушыларды практикалық қызметке, еңбекке, сонымен қатар басқа пәндерді оқыту процесінде практикалық есептер шешуге және оны ақпараттық қоғамдық өмірге дайындауға бағытталсын, - делінген. Сондықтан орта мектепті компьютерлендірудің қамтитын мәселесі тек информатика пәнін оқытумен ғана шектеліп қалмай, басқа пәндерді оқытуда компьютерді көрнекі құрал ретінде пайдалана білуді әр мұғалімге міндеттейді.
Мұғалімнің басты мақсаты - оқушыға терең де тиянақты білім беру, ал білім сапасын арттыру үшін әр мұғалім шығармашылықпен жұмыс жасауы қажет. Мұғалім пәнді өзі жетік терең білуімен қатар, оны оқушыға меңгерту үшін әр сабақта ғылым мен техника жаңалықтарын дұрыс қолдана білуі тиіс. Компьютерді сабақта орынды қолданудың бірқатар артықшылықтары бар, атап айтқанда: оқушылардың пәнге қызығушылығының артуы, оқу процесі қарқынының жоғарылауы, оқушының шығармашылық белсенділігінің көтерілуі, оқу сапасының артуы. Компьютерді оқу процесінде көрнекі құрал ретінде пайдаланып, сабақтың көрнекілігін жоғары деңгейде ұйымдастырып, өткізуге болады. Компьютерлік технологияны қолдану барысында мұғалімнің әр оқушымен жұмыс жасауға, әрқайсысына әртүрлі тапсырмалар беріп, барлық оқушы білімін бағалауға толық мүмкіндігі болады, кімнің қай тақырыпты жақсы меңгергенін немесе қай жерде білімінің осал екенін дөп басып, көмек көрсете алады. Әр оқушы өзі еңбек етеді, кейбір жағдайдағыдай тақтадан немесе жанындағы оқушыдан селқос көшіріп отырмай, есепті өзі шығаруға тырысады. Сабақта компьютерді пайдалану оқушыны шапшаңдыққа, тапқырлыққа үйретеді. Оқушы мен мұғалім қызметінде информациялық мәлімет қалыптасады. Сонымен қатар оқушының психикасы мен ойлау қабілетіне де игі әсер ететіні сөзсіз.
Жұмыс екі бөлімнен тұрады:
- Теориялық бөлім
- Практикалық бөлім
Теориялық бөлімде арифметикалық прогрессия, оның есептерін шешу жолдары туралы мәлімет PowerPoint программасы арқылы слайдтармен беріледі. Слайдтан слайдқа өту үшін тышқанды шерту қажет.
Практикалық бөлімде Паскаль тілінде құрылған программа арқылы арифметикалық прогрессия есептері құрылып экранға шығарылады, оқушы ол есептерді шешіп нәтижені енгізуі керек. Енгізілген нәтиженің дұрыс, дұрыс емес екенін көрсетіп, бағасы қойылады.
ІІ. Негізгі бөлім
- Арифметикалық прогрессияТізбектер
Жұп оң сандарды өсу ретімен теріп жазайық. Ондай бірінші сан 2, екіншісі 4, үшіншісі 6, төртіншісі 8, т. с. с. Сонда 2; 4; 6; 8; . . . тізбегі шығады.
Бұл тізбекте бесінші орында 10, оныншы орында 20, жүзініші орында 200, саны тұратыны айқын. Жалпы алғанда кез келген n натурал саны үшін оған сайкес болатын жұп оң санды көрсетуге болады, ол 2n-ге тең.
Тағы да бір тізбек қарастырайық. Алымы 1-ге тең дұрыс бөлшектерді кему ретімен жазайық:
 ;
;
 ;
;
 ;
;
 ;
;
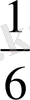 ; . . .
; . . .
Кез келген натурал сан үшін біз оған сайкес болатын бөлшекті көрсете аламыз; ол бөлшек -
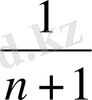 -ге тең. Сөйтіп, алтыншы орында -
-ге тең. Сөйтіп, алтыншы орында -
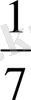 бөлшегі, отызыншы орында
бөлшегі, отызыншы орында
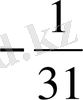 бөлшегі, мыңыншы орында
бөлшегі, мыңыншы орында
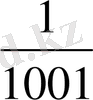 бөлшегі тұруы тиіс.
бөлшегі тұруы тиіс.
Тізбекті құрайтын сандар реті бойынша: тізбектің бірінші, екінші, үшінші, төртінші, т. с. с. мүшелері деп аталады. Тізбектің мүшелері әдетте мүшенің реттік нөмірін көрсететін индекстері бар әріптер мен белгілейді. Мысалы, а 1 , а 2 , а 3 , а 4 , т. с. с. («а бірінші, а екінші, а үшінші, а төртінші» т. с. с. деп оқиды) . Жалпы тізбектің n нөмірлі мүшесін немесе тізбектің n-ші мүшесі дегенді а n деп белгілейді. Тізбектің өзін былай белгілейміз: (а n ) .
Тізбектің мүшелер саны шектеулі болуы мүмкін екенін ескертеміз. Мұндай жағдайда оны шектеулі тізбек деп атайды. Шектеулі тізбекке екі таңбалы сандар тізбегі мысал бола алады:
10; 11; 12; 13; . . . ; 98; 99.
Тізбекті беру үшін, оның кез келген нөмірлі мүшесін табуға мүмкіндік туғызатын тәсілді көрсету керек. Тізбекті көбінесе тізбектің n-ші мүшесінің формуласы арқылы беріледі. Мысалы, жұп оң сандардың тізбегін а
n
=2n, алымы 1-ге тең дұрыс бөлшектер тізбегін b
n
=
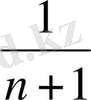 формуласымен беруге болады. Басқа мысалдар келтірейік.
формуласымен беруге болады. Басқа мысалдар келтірейік.
1-мысал. Айталық, тізбек y n =n 2 -3n формуласымен берілген болсын. n-нің орнына 1, 2, 3, 4, 5, . . . натурал сандарын қойып, мынаны шығарып аламыз:
y 1 =-2; y 2 =-2; y 3 =0; y 4 =4; y 5 =10; . . .
Қарастырып отырған тізбек былай басталады:
-2; -2; 0; 4; 10; . . .
2-мысал. Тізбек x n =(-1) n *10 формуласымен берілген болсын. Осы тізбектің тақ нөмірлі барлық мүшелері -10-ға, ал жұп нөмірлі мүшелері 10-ға тең:
x 1 =-10, x 2 =10, x 3 =-10, x 4 =10, … .
Мына тізбекті аламыз: -10; 10; -10; 10; -10; . . .
3-мысал. C n =5 формуласымен барлық мүшесі 5-ке тең тізбек былай жазылады:
5; 5; 5; 5; 5; . . .
Тізбектің берілуінің тағы бір тәсілін қарастырайық.
4-мысал. (a n ) тізбегінің бірінші мүшесі 3-ке тең, ал әрбір келесі мүшесі алдыңғы мүшесінің квадратына тең болсын, яғни
a 1 =3, a n+1 =a 2 n .
a n+1 =a 2 n формуласының көмегімен тізбектің белгілі бірінші мүшесі бойынша екінші мүшесін, сонан соң екінші мүшесі бойынша үшіншісін, үшінші мүшесі бойынша төртіншісін, т. с. с. есептеп шығаруға болады. Сонда 3; 9; 81; 6561; . . . тізбегін шығарып аламыз.
Тізбектің қандай да бір мүшесі нен бастап, кез келген мүшесін алдыңғы (бір немесе бірнеше) мүшелері арқылы өрнектейтін формуланы рекурренттік формула деп атайды (латынның recurro- қайта оралу деген сөзінен шыққан) .
2. 2. Арифметикалық прогрессияның анықтамасы.
Арифметикалық прогрессияның n-ші мүшесінің формуласы.
4-ке бөлгенде 1 қалдық қалатын натурал сандар тізбегін қарастырайық:
1; 5; 9; 13; 17; 21; . . .
Екіншісінен бастап оның әрбір мүшесі өзінің тікелей алдындағы көршілес мүшеге 4 санын қосқаннан шығады. Бұл тізбек арифметикалық прогрессияға мысал болады.
Анықтама. Екіншісінен бастап әрбір мүшесі өзінің алдындағы мүшеге бірдей санды қосқанға тең болатын тізбек арифметикалық прогрессия деп аталады.
Басқаша айтқанда, егер кез келген натурал n үшін
a n+1 =a n +d
(мұндағы d-қандай да бір сан) шарты орындалса, онда (а n ) тізбегі арифметикалық прогрессия болады.
Арифметикалық прогрессияның анықтамасынан екіншісінен бастап кез келген мүшесі мен оның алдындағы мүшенің айырмасы d-ге тең, яғни кез келген натурал n үшін
а n+1 -a n =d
Теңдігі тура екендігі шығады, d саны арифметикалық прогрессияның айырмасы деп аталады.
Арифметикалық прогрессияны беру үшін оның бірінші мүшесі мен айырмасын көрсету жеткілікті.
Мысалдар келтірейік.
Егер a 1 =1 және d=1 болса, онда мүшелері тізбектес натурал сандар болатын
1, 2; 3; 4; 5; . . .
арифметикалық прогрессия шығады.
Егер a 1 =1 және d=2 болса, онда
1; 3; 5; 7; 9; . . .
оң тақ сандардың тізбегі болатын арифметикалық прогрессия шығады.
Егер a 1 =-2 және d=-2 болса, онда берілген
-2; -4; -6; -8; -10; . . .
теріс жұп сандар тізбегі болатын арифметикалық прогрессия шығарып аламыз.
Егер a 1 =7 және d=0 болса, онда
7; 7; 7; 7; 7; . . .
арифметикалық прогрессия шығады, оның барлық мүшелері бір-біріне тең.
Арифметикалық прогрессияның бірінші мүшесі мен айырмасын біле отырып, екінші, үшінші, төртінші, т. б. мүшелерін ретімен есептеп шығарып, оның кез келген мүшесін табуға болады. Алайда прогрессияның нөмері үлкен мүшесін табу үшін бұл тәсіл қолайсыз. Есептеу жұмысы аз тәсілді табуға тырысайық.
Арифметикалық прогрессияның анықтамасы бойынша:
а 2 =а 1 +d,
а 3 =а 2 +d=(а 1 +d) +d=а 1 +2d,
а 4 =а 3 +d=(а 1 +2d) +d=а 1 +3d,
а 5 =а 4 +d=(а 1 +3d) +d=a 1 +4d.
Дәл осылайша а 6 =а 1 +5d екендігін табамыз, жалпы алғанда, а n -ді табу үшін а 1 -ге (n-1) d өрнегін қосу керек, яғни
a n =а 1+ d(n-1) .
Арифметикалық прогрессияның n-ші мүшесінің формуласын шығарып алдық.
Осы формуланы пайдалана отырып, есептер шығаруға мысал келтірейік.
1-мысал. (c n ) тізбегі c 1 =0, 62 және d=0, 24, болатын арифметикалық прогрессия. Осы прогрессияның елуінші мүшесін табамыз. Сонда:
c 50 =0, 62+0, 24*(50-1) =12, 38.
2-мысал. -122 саны
23; 17, 2; 11, 4; 5, 6; . . .
(x n ) арифметикалық прогрессияның мүшесі бола ма, осыны анықтайық.
Берілген арифметикалық прогрессияда x 1 =23 және d=x 2 -x 1 =17, 2-23=-5, 8.
Прогрессияның n-ші мүшесінің формуласын жазамыз:
X n =23-5. 8(n-1), яғни
X n =28, 8-5. 8n.
Егер 28, 8-5, 8n өрнегінің мәні -122-ге тең болатын натурал n- саны бар болса, онда -122 саны (x n ) арифметикалық прогрессияның мүшесі болып табылады.
28, 8-5, 8n=-122 теңдеуін шешейік:
5, 8n=150. 8,
n=26.
Демек, -122 саны берілген арифметикалық прогрессияның 26-мүшесі болып табылады.
Арифметикалық прогрессияның n-ші мүшесінің a n =a 1 +d(n-1) формуласын басқаша
a n =dn+(a 1 -d)
Түрінде жазуға болады. Бұдан кез келген арифметикалық прогрессияны
a n =kn+b
(мұндағы k мен b- қандай да бір сандар ) түріндегі формула мен беруге болатыны шығады.
Керісінше де тура болады:
а n =kn+b
түріндегі формуламен берілген (a n ) тізбегі арифметикалық прогрессия болып табылады (мұндағы k мен b қандай да бір сандар) .
Шынында да (а n ) тізбегінің (n+1) -ші және n-ші мүшелерінің айырмасын табамыз :
a n+1 -a n =k (n+1) +b-(kn+b) =kn+k+b-kn-b=k.
Демек, n кез келген сан болғанда a n+1 =a n +k теңдігі дұрыс және анықтама бойынша (a n ) тізбегі - арифметикалық прогрессия . Бұл прогрессияның айырмасы k-ға тең .
2. 3. Арифметикалық прогрессияның алғашқы n мүшесінің қосындысының формуласы
Алғашқы жүз натурал санның қосындысын табу керек болсын . Сандарды қосуды тікелей орындамастан, есепті қалай шығаруға болатынын көресетейік.
Ізделінді қосындыны S арқылы белгілейміз де, оны алдымен өсу ретімен, сонан соң кему ретімен орналастырып, екі рет жазып шығамыз:
S=1+2+3+…+98+99+100.
S=100+99+98++…3+2+1.
Бірінің астына бірі орналасқан әрбір қос санның қосындысы 101-ге тең. Мұндай жұптардың саны 100-ге тең. Сондықтан теңдіктерді мүшелеп қоссақ: 2S=101*100, S=
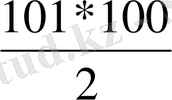 Equation. 3 =5050.
Equation. 3 =5050.
Сонымен,
1+2+3+…+99+100=5050.
Осыған ұқсас пайымдаулардың көмегімен кез келген арифметикалық прогрессияның алғашқы мүшелерінің қосындысын таба аламыз.
(a n ) арифметикалық прогрессияның алғашқы n-мүшесінің қосындысын S n деп белгілеп, осы қосындыны екі рет жазамыз, бірінші жағдайда қосылғыштарды олардың нөмерлерінің өсу ретімен, ла екінші жағдайда кему ретімен орналастырамыз:
s n =a 1 +a 2 +a 3 +a 4 +…+a n-1 +a n 3 (1)
s n =a n +a n-1 +a n-2 +a n-3 +…+a 2 +a 1 . (2)
Прогрессияның бірінің астына бірі орналасқан әрбір қос мүшесінің қосындысы a 1 +a n болады. Шынында да,
a 2 +a n-1 =(a 1 +d) +(a n -d) =a 1 +a n ,
a 3 +a n-2 =(a 2 +d) +(a n-1 -d) =a 2 +a n-1 =a 1 +a n ,
a 4 +a n-3 =(a 3 +d) +(a n-2 -d) =a 3 +a n-2 =a 1 +a n .
Мұндай жұптар саны n-ге тең. Сондықтан, (1) мен (2) теңдіктерді мүшелеп қоссақ:
2s n =(a 1 +a n ) *n.
Соңғы теңдіктің екі бөлігін 2-ге бөлсек, арифметикалық прогрессияның алғашқы n мүшесі қосындысының формуласы шығады:
S
n
=
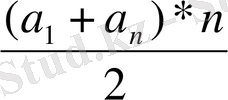 Equation. 3 (I)
Equation. 3 (I)
Арифметикалық прогрессия мүшелерінің қосындысын табуға мысалдар келтірейік.
1-мысал. 4; 5, 5; . . . арифметикалық прогрессияның алғашқы отыз мүшесінің қосындысын табайық.
Берілген арифметикалық прогрессияда a 1 =4, d=1. 5. Прогрессияның отызыншы мүшесін мүшесі n-ші мүшесін формуласы бойынша табамыз:
A 30 =4+1. 5*29=47. 5.
Енді алғашқы отыз мүшесінің қосындысын есептеп шығарайық
S
30
=
 Equation. 3
Equation. 3
Егер арифметикалық прогрессияның бірінші мүшесі мен айырмасы берілсе, онда қосындының басқа түрдегі формуласын қолданған ыңғайлы, (I) формуладағы а
n
-нің орнына a
1
+d(n-1) өрнегін қойсақ, шығатыны: S
n
=
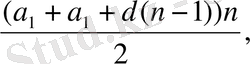 Equation. 3
Equation. 3
Яғни
S
n
=
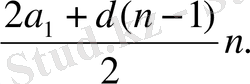 Equation. 3 (I)
Equation. 3 (I)
Қарастырылған есепті шығару үшін (II) формуланы пайдалансақ, онда есептеулер мынадай болады:
S
30
=
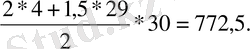 Equation. 3
Equation. 3
2-мысал. a n =5n-4 формуласымен берілген (a n ) тізбегінің алғашқы отыз мүшесінің қосындысын табайық.
(a n ) тізбегі - арифметикалық прогрессия, өйткені ол a n =kn+b(мұндағы k=5 және b=-4) түріндегі формуламен берілген.
Осы арифметикалық прогрессияның бірінші және қырқыншы мүшелерін табамыз:
a 1 =5*1-4=1, a 40 =5*40-4=196.
Енді (I) формула бойынша s 40 қосындысын есептеп шығарамыз:
S
40
=
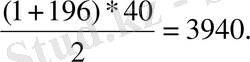 Equation. 3
Equation. 3
3-мысал. 1-ден n-ге дейінгі барлық натурал сандар қосылғыштары болып келетін 1+2+3+. . +n қосындысын табайық.
1; 2 ; 3; . . . арифметикалық прогрессияға
S
n
=
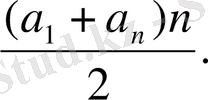 Equation. 3 формуласын қолдансақ:
Equation. 3 формуласын қолдансақ:
1+2+3+ . . . +n=
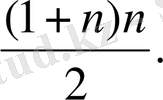 Equation. 3
Equation. 3
4-мысал. Алтыға еселік болатын және 250-ден үлкен емес барлық натурал сандардың қосындысын табайық.
Алтыға еселік натурал сандар a
n
= 6
n
формуласымен беруге болатын арифметикалық прогрессия құрайды. Осы прогрессияның неше мүшесі 250-ден артық болмайтынын айқындау үшін, 6n
 250
250
теңсіздігін шешеміз. n≤41
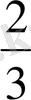 болады. Демек, прогрессияның қосындысын табу керек болатын мүшелерінің саны 41-ге тең.
болады. Демек, прогрессияның қосындысын табу керек болатын мүшелерінің саны 41-ге тең.
Сонда:
a 1 =6*a 41 =6*41=246,
S
41
=
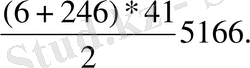 Equation. 3
Equation. 3
2. 4. Есеп құрастыратын программа дайындау
Арифметикалық прогрессияға берілген есептерді құрастыру алгоритмі
Мектеп алгебра курсының 9 сыныпқа арналған оқулығында арифметикалық прогрессияға берілген тақырып үш тақырыпшадан тұрады: “Тізбектер”, “Арифметикалық прогрессияның анықтамасы. Арифметикалық прогрессияның n -ші мүшесінің формуласы”, “Арифметикалық прогрессияның алғашқы n мүшесінің қосындысының формуласы”. Дипломдық жұмыста аталған үш тақырыптан есептер алынып, сол есептерді құрастыру программалары қарастырылды. Программада әр тақырыпқа берілген есептерге сәйкес процедуралар алынған.
“Тізбектер” тақырыбына сәйкес esep1 процедурасы жазылды. Онда мынадай есеп түрі қарастырылды: ( b n ) тізбегі b n =n 2 -n формуласымен берілген. Табыңдар: а) b 5 ; ә) b 10 ; б) b 50 . Бұл есепте b -ның коэффициенттері 5, 10, 50 болғанда b n =n 2 -n формуласымен b n -ді табу керектігі айтылғандықтан, программада n -нің мәндері кездейсоқ сандарды таңдау операторы арқылы таңдалып, соған сәйкес b n -нің мәндері есептеледі. Программа арқылы экранға есептің шартына таңдалған n -нің мәндері қосып шығарылған соң, b n -ді табу сұралады. Ал b n -нің мәні программада есептеліп, ол енгізілген мәнмен салыстырылады, содан соң оның дұрыс, дұрыс емес екендігі хабарланады.
“Тізбектер” тақырыбына алынған екінші есеп esep2 процедурасында қарастырылды. Екінші есеп мына түрде болды: “ n -ші мүшесінің формуласымен берілген тізбектің алғашқы 5 мүшесін табыңдар: x n =2n-1; x n =n 2 +1; x n =2 n-1 . Жоғарыдағы сияқты тізбектің формуласы программаға енгізіліп, n -нің мәні кездейсоқ сандарды таңдау операторымен таңдалып, x n -нің мәндері 1-ден бастап n -ге дейін кезекпен есептеліп, программа арқылы енгізілетін сандармен кезекпен салыстырылады, енгізілген жауаптың дұрыс, дұрыс емес екендігі анықталады.
Esep3 процедурасында “Тізбектер” тақырыбының мына түрдегі есебі қарастырылды: (bn) тізбегінің алғашқы 4 мүшесін теріп жазыңдар, мұндағы b 1 =5, b n+1 =b n +k . Программада кездейсоқ таңдау әдісі арылы тізбектің алғашқы мүшелерінің саны, b 1 -дің және k -ның мәндері таңдалып, есептің шартындағы орындарына қойылып экранға шығарылды. b n+1 -дің мәні программада есептеліп, енгізілген сандармен салыстырылып, оның дұрыс, дұрыс еместігі хабарланады.
“Арифметикалық прогрессияның анықтамасы. Арифметикалық прогрессияның n -ші мүшесінің формуласы” тақырыбына төрт есеп құрастырылды:
- Егерa1=5, d=3 болса, ондаan-ді табыңдар.
- Арифметикалық прогрессияныңn-ші мүшесін табыңдар: 3; 8; … .
- а) Арифметикалық прогрессияның айырмасын табыңдар. Мұндағыa1=3, a8=25.
б) Арифметикалық прогрессияның бірінші мүшесін табыңдар: Мұндағы d =4, a 7 =45.
- Егера4=15 жәнеa9=34 болса, арифметикалық прогрессияның бірінші мүшесі мен айырмасын табыңдар.
Олар esep4 , esep5 , esep6 , esep7 процедураларында өрнектелді. Аталған процедуралардың барлығында арифметикалық прогрессияның алғашқы мүшесі а 1 , айырмасы d , есептің шартына сәйкес мүшелерінің сандары кездейсоқ сандарды таңдау операторы арқылы таңдалып алынып, прогрессияның n -ші мүшесі a n =a 1 +d(n-1) формуласы арқылы есептеліп, есептің шартындағы сәйкес орындарына қойылып, есептердің шарттары экранға кезекпен шығарылады. Және енгізілген мәндермен салыстырылып, олардың дұрыс, дұрыс емес екендігі анықталады.
Арифметикалық прогрессияға берілген үшінші тақырыпқа екі есептің түрін құрастыру esep8 және esep9 процедураларында қарастырылды. Бұл процедураларда есептің мынадай түрлері алынған:
- Арифметикалық прогрессияның алғашқыnмүшесінің қосындысын табыңдар. 5; 9, … .
- Арифметикалық прогрессияныңа5=9 жәнеa9=27 болғанда, алғашқы 15 мүшесінің қосындысын табыңдар.
Аталған процедураларда а 1 , d, n -дердің мәндері кездейсоқ таңдалып, a n =a 1 +d(n-1) және S n =(2a 1 +d(n-1) /2*n) формулаларымен прогрессияның n -ші мүшесі мен алғашқы n мүшесінің қосындысы есептеліп, олардың мәндері есептің шарттарындағы сәйкес орындарына қойылды. Және олардың енгізілген мәндермен бірдейлігі тексеріліп, дұрыс, дұрыс еместігі анықталды.
Программада барлық таңдалатын сандардың оң немесе теріс сан болуы, бүтін немесе бөлшек сан болуы, сандардың таңбаларының дұрыс жазылуы толық қарастырылған. Таңбаларды ауыстырып отыру үшін қосымша кездейсоқ сан таңдалған. Ол сан жұп сан болса, таңдалған басқа санды өзінің теріс мәнімен ауыстырады:
if m/2=int(m/2) then a1:=-a1;
Бөлшек сандарды шығару үшін үлкен сандар таңдалып, оны 10-ға бөліп, экранға үлгі бойынша үтірден кейін бір сан жазылып шығатындай етіп қарастырылды. Мысалы: a1:=(15+random(20) ) /10; writeln(a1:2:1) ;
Сонымен қатар, программада берілген тақырыптарды жеке-жеке алуға, немесе барлық тақырыптарды бірден қарастыруға болады. Бұлардың әрқайсысында дұрыс жауаптар саны есептеуіш айнымалы арқылы есептеліп, тексеріп бағалауға болатын мүмкіндік енгізілген.
Программаның соңында дұрыс берілген жауаптардың санына байланысты оқушылардың бағалары экранға шығарылады. Бағалау мынадай принциппен жүргізілді: дұрыс берілген жауаптардың проценттік мөлшері есептеледі, осы проценттік мөлшерге байланысты баға қойылады. Ол программада төмендегідей болып белгіленген: 85%-100% дұрыс жауапқа “5” деген баға, 75%-84%-ке - “4”, 60%-74%-ке - “3”, дұрыс жауаптар мөлшері 60%-тен төмен болса “2” деген бағалар қойылады.
Программа Турбо Паскаль тілінде жазылған, мұнда компилияциялау арқылы орындалатын . ехе-файл құрылатындықтан, программа барлық типтегі компьютерлер үшін оңай көшіріліп, орындалуы өте қарапайым болып табылады. Әрі қазіргі кезде кеңінен қолдау тауып келе жатқан Delphi программалау тіліне оңай аударылады.
2. 5. Программа тексті
program arifmetika_progressya;
uses crt;
label 8;
var t, bb:integer; m:char;
aj:string[15] ;
pr:real;
procedure esep1;
label 1;
var b, i, j, k, n, bi, bj, bk:integer;
begin
randomize;
1: i:=random(5) ;
j:=random(10) ;
k:=random(50) ;
if (i=j) or (i=k) or (j=k) then goto 1;
writeln;
writeln(' 2 ') ;
writeln(' (bn) тiзбегi bn=n -n формуласымен берiлген. ') ;
writeln('Табыңдар: ') ;
write('a) b', i, '=') ; readln(bi) ;
if bi<>sqr(i) -i then writeln('Дұрыс емес, дұрыс жауабы ', sqr(i) -i) else begin writeln('Дұрыс') ; bb:=bb+1 end;
write('ә) b', j, '=') ; readln(bj) ;
if bj<>sqr(j) -j then writeln('Дұрыс емес, дұрыс жауабы ', sqr(j) -j) else begin writeln('Дұрыс') ; bb:=bb+1 end;
write('б) b', k, '=') ; readln(bk) ;
if bk<>sqr(k) -k then writeln('Дұрыс емес, дұрыс жауабы ', sqr(k) -k) else begin writeln('Дұрыс') ; bb:=bb+1 end;
end;
procedure esep2;
label 1;
var i, j:integer;
a:array [1. . 10] of real;
begin
randomize;
1: i:=random(7) ;
if i<3 then goto 1;
writeln;
writeln(' n-шi мүшесiнiң формуласымен берiлген тiзбектiң') ;
writeln('алғашқы ', i, ' мүшесiн табыңдар:') ;
writeln('а) xn=2n-1') ;
for j:=1 to i do
begin
write(j, '-мүшесi=') ; readln(a[j] ) ;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz