Дифференциалдық геометрия

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 73 бет
Таңдаулыға:

Кіріспе

Дифференциалдық геометрия пәні - бұл геометриялық бейнелерді қарастыратын математиканың бөлігі. Геомертиялық бейнелер деп отырғанымыз ол : біріншіден қисықтар мен беттер және олардың шексіз аз өлшемдегі талдау әдістері. Дифференциалдық геометрияның ерекшелігі ол қисықтар мен беттердің қасиеттерін аз бөліктерде зерттейді, яғни қисықтар мен беттердің мүмкіндігінше кішігірім бөлшектеріндегі қасиеттерін қарастыру[1].
Дифференциалдық геометрия математикалық талдау пәнімен қатар және тығыз байланыста бірге дамыды деседе болады. кейбір жағдайларда математикалық талдаудың өзі геометрияның есептернінен бастау алады. Мысалы, қисыққа жүргізілген жанама туынды ұғымынан бұрынырақ белгілі болып, оның дамуына себепкер болды немесе аудан және көлем ұғымдары интегралдық пайда болуына және дамуына жол ашты.
Дифференциалдық геометрияның алғашқы есептері мен ұғымдары математикалық талдаудың дүниеге келуімен байланысты және ол туралы мәліметтер Г.Лейбництің , И.Ньютонның тағы басқа 17 ғасырдың математиктерінің жұмыстарында кездеседі. Дифференциалдық геометрия бөлек пән ретінде Л.Эйлер және Г.Монж жұмыстарында қалыптаса бастады. Г.Монжтың ең танымал болған 1795 жылы жазылған Талдауды геометрияғы қолдану жұмысы.
Дифференциалдық геометрияның келесі даму уақыты К.Гаусстың атымен байланысты. Ол өзінің Қисық беттерді жалпы зерттеу жұмысында 1827 жылы беттің ішкі геометриясы идеясын дамытады.
Н.И. Лобачевский мен Б.Риман жұмыстарында кеңістік ұғымын жалпылау бағыты дамытылған . Геометрия негіздері түбінде жатқан гипотезалар атты Б.Риманның танымал лекцияларында (1854 ж.) кеңістіктер теориясының негіздері берілген , енді олар риман кеңістіктері деп аталады. Содан кейін тензорлық талдау риман геометриясында көп қолданылатын аппарат болды.
Дифференциалдық көпбейнеліктерді енгізу дифференциалдық және геометриялық кеңістіктерді локалды қарастырудан жалпы зерттеуге өтуге көмектеседі.
Курсың негізгі мақсаты- классикалық дифференциалдық геометрияның әдістерін және көрнекті бейнелерді қолданып, білімгерлерді қазіргі дифференциалдық геометрияның негізгі түсініктерімен таныстыру болып табылады.

I бөлім
Қисықтар теориясы
Жалпы қисықты біз , жазықтықтағы немесе кеңістікте қозғалатын нүктенің ізі деп елестете аламыз.
Қисықтарды анықтау үшін келесі жолдарды қарастыруға болады, ол үшін біріншіден кәдімгі қисық түсінігін , содан соң параметрмен берілген жалпы қисықтарға түсінік береміз. Қисықтарды дифференциалдық тұрғыдан түсіндіру үшін , қисықтарға қосымша геометриялық шектеулер қоюлу керек. Мұндай шектеулер тегіс қисықтарға әкеледі. Ал одан да жоғарғы шектеулер қисықтарды регулярлы қисықтарға әкеледі. Мұндай қисықтар үшін , қисықтардың ( қисықтық бұрылу) маңызды скалярлық сипаттамалары анықталды. Бұл қасиеттерді қисықтардың локалды құрылымдарын зерттеуде қолдана отырып, қажетті және пайдалы қатынастарды алуға болады[4].

§1. Қарапайым жазық қисықтар
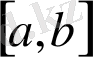сегментінде аргументі (параметрі) t болатын үзіліссіз 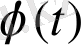және 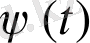функциялары берілсін.
х және у координаталары төмендегі ара қатыспен анықталатын, 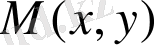нүктелерінің L жиынын қарастырайық.
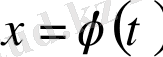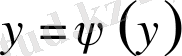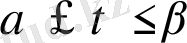, , . (1)
Егер 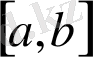сегментінде t параметрінің әртүрлі мәніне L жиынның әртүрлі нүктелері сәйкес келетін болса, онда L жиынын қарапайым жазық қисық деп атаймыз.
Егер t параметрін физикалық шама ретінде ,яғни - уақытпен деп есептесек, онда қисықты жазықтықтағы нүктенің қозғалысының троекториясы деп елестетуге болады.
Координаталары (1) теңдеумен анықталатын M(x,y) нүктесін L қисығының нүктесі деп атаймыз. t параметрінің шеткі мәндері α және β -ға сәйкес болатын A және B нүктелерін L қисығының шекаралық нүктелері деп атаймыз (1 сурет).

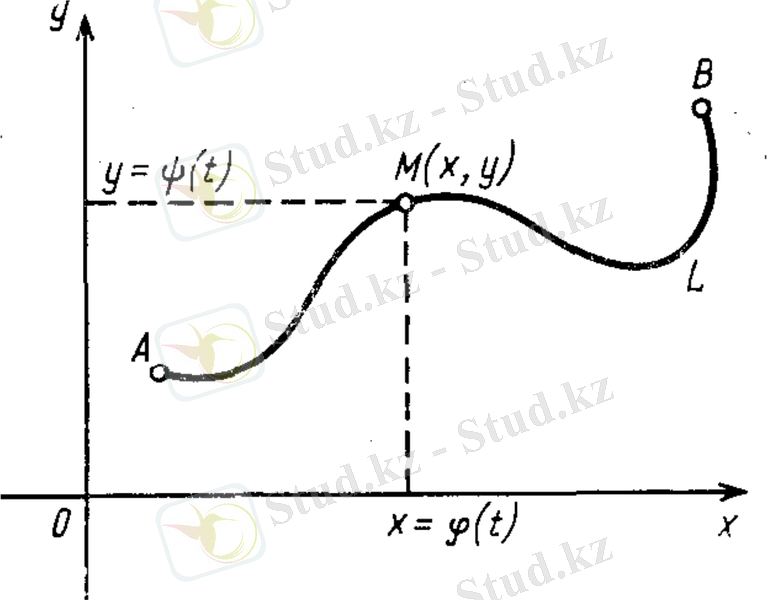
1 сурет. M(x,y) нүктесінің (1) заңдылық бойынша L қисығымен А нүктесінен В нүктесіне дейінгі қозғалысы.

2 сурет. L1 және L2 қарапайым қисықтарын қосқанда пайда болатын L тұйық қисығы.
Қарапайым жазық қисықтарға мысал ретінде [α,β] сегментінде үзіліссіз болатын y=f(x) функциясының графигін айтуға болады. Бұл графиктер x және y координаталары x=t, y=ft, α=t=β қатынастарымен M нүктесінің жиыны. t параметрінің әртүрлі шамаларына графиктердің әр түрлі нүктелері сәйкес келеді. Енді келесі ескертулерді қисықтарды зерттегенде ескергеніміз жөн.
1 ескерту. Бір қарапайым қисық әртүрлі жолмен параметрленуі мүмкін. Мысалы, L қарапайым қисығының параметрленуін қарастырайық. Ол келесі x=φt, y=ψt, α=t=β параметрлерімен алынған, мұндағы t параметрін басқа s параметрімен түрлендіруге болады, яғни s:x=φts,y=ψts,α1=s=β1.
2 ескерту . Қарапайым тұйықталған жазық қисықтар туралы ұғымдарды қарастыру маңызды болып табылады. L1 және L2- екі қарапайым жазық қисықтарының берілуі келесі тұжырымдамаларға сәйкес берілсін дейік: біріншіден, әрбір L1 қисығының шеткі нүктесі L2 қисығының шеткі нүктесіне сәйкес келеді; Екіншіден, L1 және L2 қисықтарының кез келген шеткі емес нүктелері әр түрлі . L1 және L2 қисықтарының қосындысы қарапайым тұйықталған жазық қисық деп аталады. Қарапайым тұйық жазық қисықтарды да (1) теңдеуімен параметрлеуге болады.
Жоғарыдағы тұжырымдамаларымыздың дұрыстығын келесі мысалмен көрсетейік [4,8].
Мысалы. M(x,y) нүктелерінің жазықтықтағы қозғалысы төмендегі параметрлік теңдеулермен берілсін дейік, t параметрі -infinity және +infinity өзгереді
x=at2-1t2+1 , y=att2-1t2+1, a0 ,
Бұл белгілі строфоида деп аталатын қисықты көрсетеді(3 сурет).

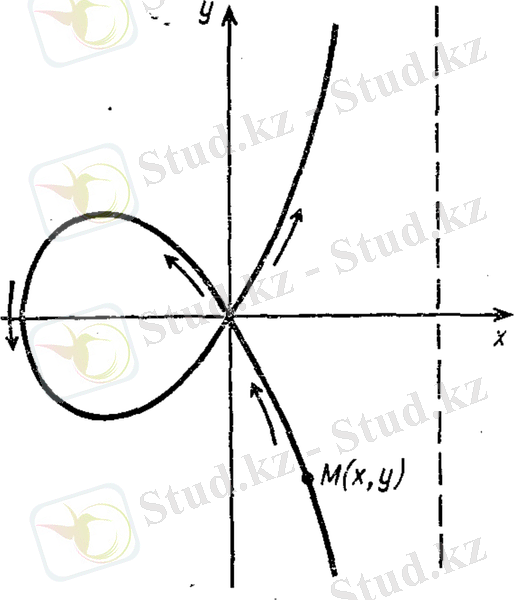
3 сурет. Строфоида қисығы
Суретте көрініп тұрғандай t параметрі өзгергенде көрсетілген шектері қозғалыста строфоиданың M(x,y) нүктесі O(0,0) бас координатаға екі рет беттеседі. Біз қарастырып отырған тізбек нүктелері қозғалыстағы ереже, строфоида нүктелері t параметріне жауап беретін әр түрлі мағынада түрліше есептеледі . Строфоидағы әрбір нүкте t параметріндегі нүктелерге жауап береді . Строфоиданы қарапайым жазық қисықтардың бірігуі депте қарастыруға болады.
Параметрлік тұрғыдан берілген қисықтың берілуін талдайық. t параметрінің өзгеру облысы {t} деп белгілесек. Ол түзудегі байланысқан келесі жиындарды беруі мүмкін :
сегмент;
жартылай сегмент немесе тұйықталған жартылай түзу;
интервал , ашық жарты түзу немесе түзудің барлық бойы.
t параметріның функциялары φ(t) және ψt функциялары {t} байланысқан жиынында үзіліссіз дейік.
Онда төмендегі қатынастар
x=φt,y=ψt, t ϵ t (2)
L жазық қисығының параметрлік теңдеулері екендігін көрсетеді .
Сонымен бірге , L қисығының да параметрлік (2) теңдеулерімен тығыз байланысты болады.
§2. Кеңістіктегі қисықтар.
Кеңістіктегі қисықтар түсінігін де жазық қисықтар ұғымы сияқты түсіндіруге болады.
Кеңістіктік қисық түсінігі тегіс қисық түсінігімен толық үйлестік табады.
Егер 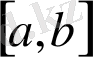сегментінде t параметрінің әртүрлі мәніне L жиынның әртүрлі нүктелері сәйкес келетін болсын дейік [2,3].
Анықтама. x,y және z координаталары келесі ара қатыстармен анықталатын
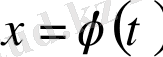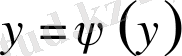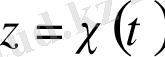, , , , (3)
М нүктелердің L жиынын жай кеңістіктегі қисық деп атаймыз ,мұндағы - 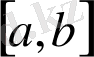сегментіндегі үзіліссіз функциялар.
Егер t параметрі 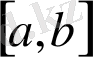сегментіндегі әртүрлі мағынада жауап беретін болса , онда жиынның әртүрлі нүктелеріне сәйкес болады.
(3) қатынасты кеңістіктегі қисықтың параметрлік теңдеуі деп атайды.
Ескерту. n-өлшемді Enевклид кеңістігінде мына қатынас арқылы қисық анықталады
x1=φ1t,x2t,...,xnφnt,
Мұндағы , t параметірі {t} байланысқан жиында өзгереді, ал φi(t) функциясы үзіліссіз болады.
Қисықтарды екі беттің қиылысы ретінде де беруге болады.
Ф1 және Ф2 беттердің теңдеулері 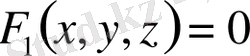және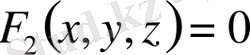сәйкес болсын.
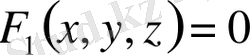(4)
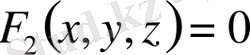(5)
(4), (5) теңдеулер жүйесін Ф1 және Ф2 беттерді қиып өтетін сызықтардың, L қисықтың теңдеуі ретінде қарастыруға болады (4 сурет).

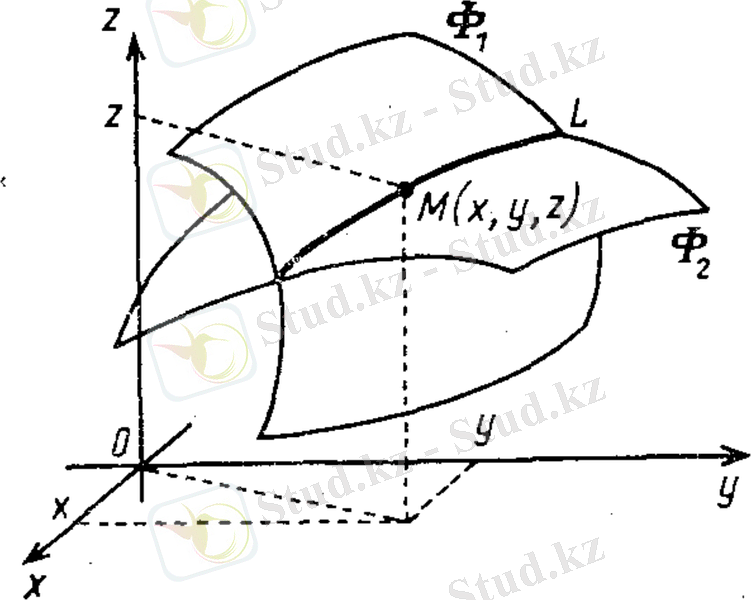
Сурет 4. Кеңістіктегі қисықтар беттегі сызықтардың қиылысуы
Қисықтың М нүктесінің х,у және z координаталарының (4) және (5) теңдеулерін қанағаттандырады.
Егер (4) ,(5) теңдеулер жүйесін y және z - ке қарағанда шешсек , яғни x- ты y және z функцияларының аргументі ретінде қарастырсақ:
y=ψx,z=χ(x)
L қисығының маңайы болуы мүмкін егер мына шарт дәл М нүктесінде орындалса
dF1dydF1dzdF2dydF2dz !=o
Содан x- ты t параметрі ретінде таңдап , қисықтың параметрлік теңдеуін аламыз
x=t,y=ψt,z=χt.
Мысалы, Вивиани қисығы өзінің сызықтық қиылысуын сферада радиусы a және дөңгелек цилиндрда үстінгі диаметрі a, сфераның центрі арқылы біреуі өтеді.Егер бас координатаға сфераның центріне орналастырсақ , OZ осін цилиндрдің үстінгі жасаушысына бағыттасақ ,сферасының теңдеуі Φ1 және Φ2 цилиндрлік бетті мынадай түрге келеді [4].
x2+y2+z2=a2, x2+y2-ax=0.
Осы Вивиани қисықтық теңдеуі (5 сурет).

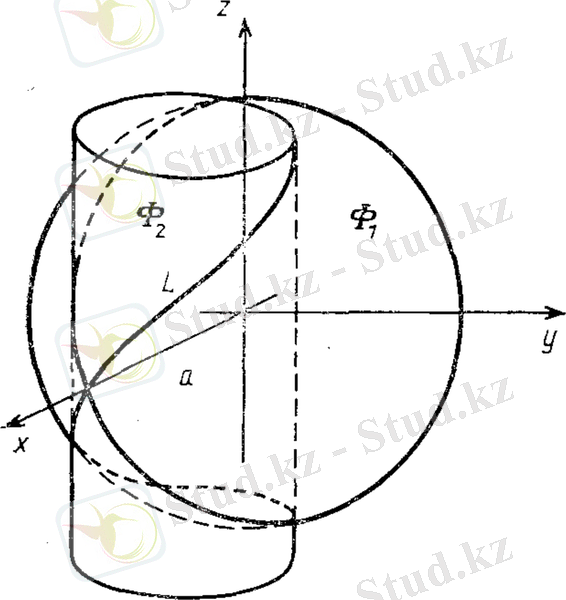
5 сурет . Вивиан қисығы.
Егер x-ты t-тың параметрі деп алсақ , онда келтірілген жүйеден Вивиани қисығының жеке бөлігінің параметрлік теңдеулерін аламыз:
x=t,y=+-at-t2, z=+-a2-at, 0=t=a.

§3. Векторлық функцияның годографы.
t-R түзуіндегі нүктелердің байланысқан жиыны болсын ( ол сегмент , жартылай сегмент ,аралық және тұйық жарты түзу ,бүкіл түзу болуы мүмкін) [1,3].
{t} байланысқан жиынында r=r(t) векторлық функциясы берілген дейміз, егер tϵ{t} -нің әрбір мәніне ережесі бойынша r(t) векторы сәйкестендірілетін болса. Егер бүкіл векторды бас координатадан бастап алсақ, t параметрі өзгергенде {t} жиынында rt векторының соңы M нүктесі сызатын қисықты r(t) векторлық функциясының годограф деп атаймыз.(6 сурет).

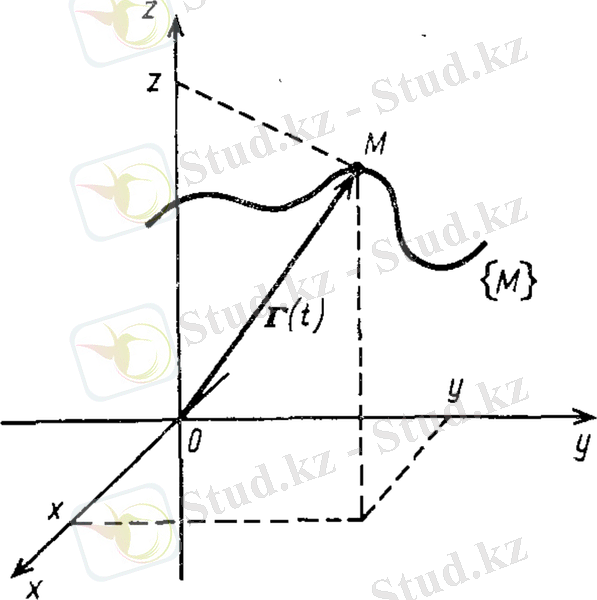
6 сурет. Векторлық функцияның годографы.
Векторлық функция үшін де скалярлы функцияларға қатысты үзіліссіздік пен шектер түсінігін толық ұқсас.
Анықтама. b векторы rt векторлық функциясының шегі деп аталады t--a (α нүктесінде), егер кез келген ε0 саны үшін δ0 бар болып, мұндай tϵt барлығы үшін ,0t-αδ шарты қанағаттандырылып , келесі [5].
rt-bε
теңсіздігі орындалса және бұл шек келесі түрде белгіленеді.
r(t)t--α--b, limt--αrt=b (6)
Анықтама. rt векторлық функциясы t0∈{t} нүктесіне үзіліссіз деп аталады,егер rtt--t0--r(t0) . Векторлық функция {t} жиынының әр нүктесінде үзіліссіз деп аталады, егер ол осы жиынның әр нүктесінде үзіліссіз болса [1].
r=r(t) векторлық функциясы берілсін, x,y,z координаталары r(t) айнымалы векторында t∈{t}функциясының параметрі болады:
x=φt,y=ψt,z=χt (7)
Егер ,сонымен қатар i,j,k-ось координаталары бірлік векторы десек , онда
rt=φti+ψtj+χ(t)k.
Егер (7) функция берілген, r=r(t) векторлық функциясының координаталары деп алсақ болады.Осыдан көруге болады,егер r(t)t--α--b , (7) функция t--α шегі болады, b векторының координаталары тең қатысты. rt үзіліссіздігінен α нүктесі шығады.
Дұрыс және кері:t--α шегінің (7) функциясынан шығады шегі rt векторлық функциясының координаталары екені анықталады.
Вектор функциясының үзіліссіздігі де скаляр функциялар сияқты анықталады.
Тұжырымдама. Егер rt, Rt векторлық функциялары және λt скалярлы функциясы үзіліссіз болса , онда келесі функцияларда үзіліссіз:
rt+-Rt,λtrt,rt,Rt,rtxRt
Дәлелдеу ,мысалы, (rt,R(t)) функцияларының үзіліссіздігі
φt,ψt,χ(t) -берілген rt және Φt,ψt,χt векторлық функцияларының координаталары-R(t) болады.
Содан
rt,Rt=φtΦt+ψtΨt+λ(t)X(t)
скалярлы функцияның үзіліссіздігі және туындысы мен жалпы саны соңғы теңдеуін скалярлы теңдеуі (rt,R(t)) үзіліссіз.
r=rt-[α,β ] сегментінде үзіліссіз векторлық функция t параметрінің әр түрлі мағынасы осы сегменттен әр мағынасы векторлық функция, годограф - жай қисық болады.Біз айтамыз ,қисық параметрлік тапсырма (7) теңдеудің көмегіне қатысты,r=r(t) векторлық функциясының годографы.Параметрлік және векторлық тапсырма қисықтары теңдей.
Біз келесі терминалогияны пайдаланып:"L- қисығы r=r(t) векторлық функциясында берілген" немесе " r=rt-L қисығының векторы"
§4. Тегіс және регулярлы қисықтар.
L қисығы төмендегі параметрлі теңдеулермен берілсін
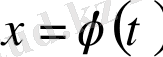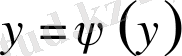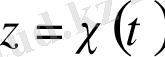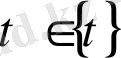, , , (1)
(мұндағы 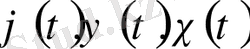- жиынындағы үзіліссіз функциялар). tпараметрінің мәніне сәйкес келетін L қисығындағы нүктені Mарқылы, ал tмәнінің кез келген аймағындағы t параметрінің мәніне сәйкес келетін L қисығындағы нүктені M деп белгілейік. Бұдан, егер болса, онда болатыны анық[1,2].
Анықтама. Егер ұмтылғанда, M0T түзуі мен М0М айнымалы түзу арасындағы θ бұрышы нөльге ұмтылса, онда M0T түзуін М нүктесі арқылы өтетін L қисығына жанама деп атаймыз(7 сурет).

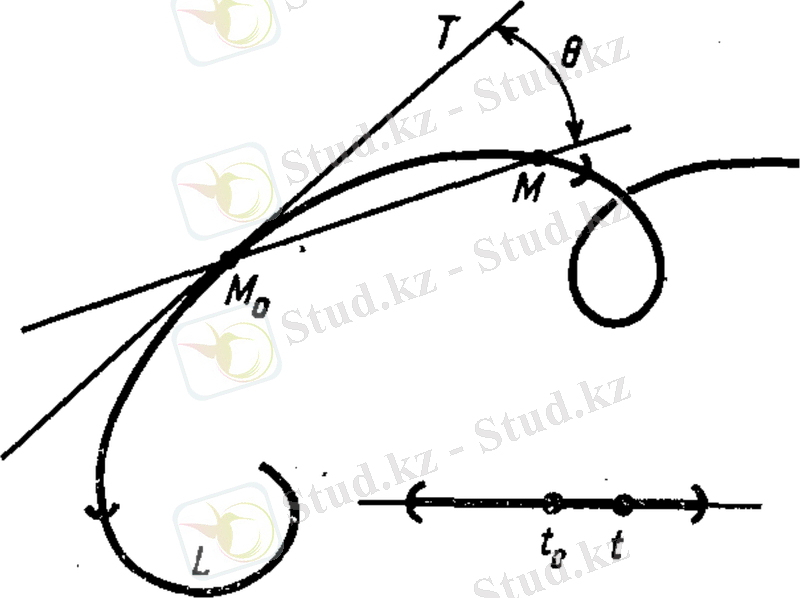
7 сурет. Мнүктесіне жүргізілген жанама.
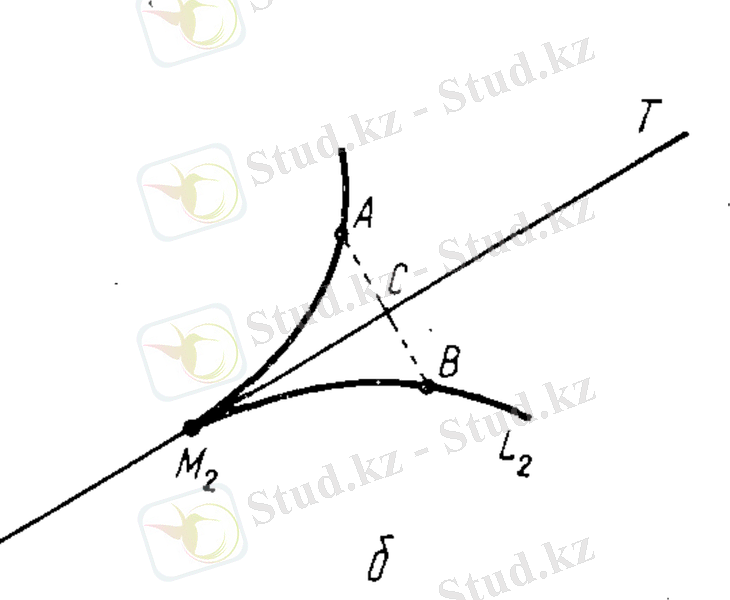
Анықтама. Егер L қисығындағы Мнүктесі арқылы өтетін жанама табылып және L қисығындағы Мнүктесінің аймағы жанамаға проекцияланатын болса, онда L қисығы Мнүктесінде тегіс деп аталады[4,7].
Тегіс емес қисықтың нүктелері ерекше деп аталады.(8 сурет). M0 нүктесінің маңайы L-қисығында көпмүшелігі M нүктесінде қисығы.

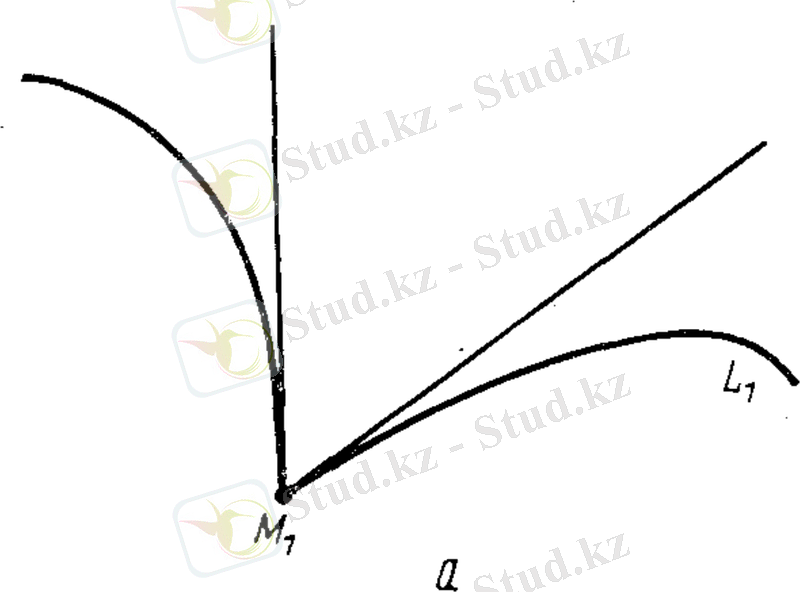
8 сурет. Ерекше нүктелер.

Тегіс қисықтың жеткілікті шарты. мәнінің аймағында үзіліссіз туындысы 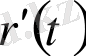бар болатын 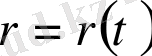векторлық функциямен L тегіс қисығы берілсін. Сонымен қатар, 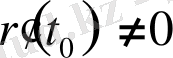. Сонда, L қисығы мәніне жауап беретін М0 нүктесінде тегіс қисық болып табылады [7].
§5. Векторлық функцияларды дифференциалдау және интегралдау.
rt векторлық функциясы {t} жиынында анықталсын.
Анықтама. r(t) векторлық функциясының t нүктесінде туындысы болады, егер келесі шек бар болса, яғни
lim∆t--0rt+∆t-r(t)∆t.
r(t) векторының туындыны келесі түрде өрнектейді: drdt,r't.
Векторлық функцияның туындысының геометриялық мағынасы төмендегі cуретте көрсетілген(9 сурет) .

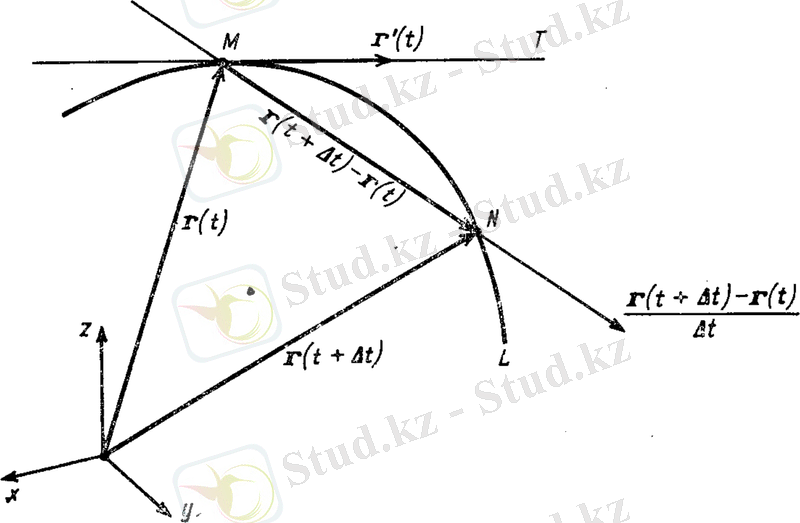
9 сурет.
Егер r'(t)!=0 болса, онда r(t) векторлық функциясы L годографының M нүктесінде жанамасы бар болады және r't векторы осы жанаманың бойымен бағытталады.
φt,ψt,χt-r(t) векторлық функциясының координаталары болсын.
Егер rt функциясы t нүктесінде туындысы болса, онда әрбір φt,ψt,χt функциялардың да t нүктесінде туындысы болады.
Бұл тұжырымды кері айтасақта болады: егер φt,ψt,χt функцияларының t нүктесінде туындысы болса, онда r(t) векторлық функциясының да осы нүктеде туындысы табылады [3].
Егер rt,Rt және λ(t) функциялары әрқайсы t нүктесінде туындылары болса, онда rt+-Rt,λtrt,rt,Rt,rtxRt функциялары да әр нүктесінің туындысы табылып келесі қатынас орындалады:
r+-R'=r'+-R',λr'=λ'r+λr',
((r,R))'=r',R+r,R',(rxR)'=r'xR+rxR' .
r'(t) векторлық функциясы туындысы деп аталады екінші ретті туындысы rt векторлық функциясында .Осыған ұқсас үшінші ретті туындысы анықталады.
Екінші және үшінші ретті туындысы анықталады мына қатынас арқылы r''(t) және r'''(t) . n-ші ретті туындысы үшінде қолданылады rntжәне dnrdtn.
Егер φt,ψt,χt-rtвекторлық функциясының координаталары ,онда
r(n)t=φnti+ψntj+χntk. (2)
Егер r(t) векторлық функциясы үзіліссіз барлық n-ші ретті туындысында , жазады r(t)∈Cn.
r(t)∈Cn-1 функциясы t0 нүктесінің кейбір маңайында rn(t0) туындысы бар болса. Онда r(t) Тейлор формуласының дұрыстығы:
rt=rt0+r't0t-t0+12!r''t0t-t02+...+1 n!rnt0t-t0n+ot-t0n,(3)
мұнда ot-t0n векторы өзінен үлкен ретті қарағанда (t-t0)n, т.б.
o((t-t0)n)(t-t0)nt--t00.
Формула (3) былай алынады.r(t) векторының φt,ψt,χt функцияларының координаталары Тейлор формуласында қалдық мүше Пеано түрінде.
φt=φt0+φ't0t-t0+12!φ''t0t-t02+...+1 n!φnt0t-t0n+ot-t0n,
ψt=ψt0+ψ't0t-t0+12!ψ''t0t-t02+...+1 n!ψnt0t-t0n+ot-t0n,
χt=χt0+φ't0t-t0+12!χ''t0t-t02+...+1 n!χnt0t-t0n+ot-t0n.

Бірінші қатынас i орт көбейтіндісі , екінші орт-j, үшінші орт-k , (1) және (2) формуласын қолданып (3) теңдеуін аламыз.
Риман интегралы αβr(t)dt r(t) векторлық функциясы үшін,α=t=β, анықталады интеграл шегінің суммасы [5].
i=1nr(ξi)Δti
Сонымен,maxΔti--0 (α=t0t1...tn-1tn=β,∆ti=ti-ti-1, ξi-
сегмент әр нүктесінде [ti-1,ti]).
Интеграл қатынасы.
1.αβrt+Rtdt=αβr(t)dt+αβRtdt.
2.αβrtdt=αβφti+ψtj+χtkdt=(αβφ(t)dt) i+(αβψ(t)dt)j+(αβχ(t)dt)k.
3.αβrtdt=αγrtdt+γβrtdt αγβ.
4.αβλrtdt=λαβrtdt λ-сан.
5.Егер r-тұрақты вектор ,онда
αβr,Rtdt=r,αβRtdt,αβrxRtdt=rxαβRtdt .
6.ddτατrtdt=rτ.
Тегіс қисықтың жеткілікті шарты
1 теорема. (тегіс қисықтың нүктедегі жеткілікті шарты). L қисығы келесі r=r(t) векторлық функциясымен берілсін және t0∈t аймағында r'(t) туындысы болсын. Сонымен қатар оның r'(t0)!=0 . Онда L қисығы t0 мәнінде анықталатын M0 нүктесінде тегіс қисық деп аталады.
r'(t0)!=0 болғандықтан M0 нүктесінде L қисығына жүргізілген жанама M0T болады. Сондықтан M0 нүктесінің аймағындағы L қисығына жүргізілген жанамаға проекцияланатын көрсетсек жеткілікті. Мұны дәлелдеу үшін кері тұжырым әдісін қолданайық, яғни жоғарыдағы тұжырым орындалмайды дейк. Онда келесі екі тізбек болады t'k--k--infinityt0, t''k--k--infinityt0 және олардың rt"k-r(t'k) айырымы r'(t0) векторына ортогональды болады. Тейлор формуласы бойынша n=1 болғанда t'k жіктелу центрі үшін келесі тендікті аламыз.
rt"k=rt'k+r't'kt"k-t'k+0t"k-t'k.
Бұдан r(t'k) шегеру арқылы жо,арыдағы айырым үшін келесі қрнекті аламыз.
rt''k-rt'k=rt'kt"k-t'k+0t"k-t'k.
Соңғы өрнекті r'(t'0) -ға скаляр көбейтейік. rtk''-r(tk') айырымының r'(t0) векторына ортогональ екендігін ескере отырып, қатапайым түрлендіру жасап келесі теңдікті аламыз.
r't'k, r't0t"k-t'k=0t"k-t'k.
tk'--t0 десек ,онда r't0!=0 және r'(tk')--r'(t0). Бұл жағдйда соңғы теңдңктің сол жағы О(tk"-tk') тең, ал оң жағы о(tk"-tk') тең.Бұл қарам қайшылықты тудырады. Олай болса, жоғарыдағы келтірілген тұжырымдамамыздың дұрыстығы дәлелденді.
2 теорема . L қисығы келесі r=r(t) векторлық функциясымен берілсін, және t∈t аймағында үзіліссіз r'(t) тундысы болсын. Егер кез келген t∈t үшін r'(t)!=0 шарты орындалса, онда L қисығын тегіс деп атаймыз.
Регулярлы қисықтар.
Тегіс L қисығы келесі r=r(t) векторлық функциясымен берілсін. Егер r(t)∈Cn,n=2 болса, онда L қисығы регулярлы қисық деп аталады. (Cn класындағы қисықтар).
Регулярлы қисықтың жеткілікті шарты.
r=r(t) t∈t векторлық функциясы арқылы берілген L қисығы регулярлы болу үшін , t жиыны үшін келесі шарттың орындалуы жеткілікті, яғни r(t)∈Cn,n=2 r'(t)!=0 .
Ескерту. Егер r't туындысы үзіліссіз және r'(t0)!=0 онда t0 нүктесінің аймағы үшін r'(t)!=0 .Сонымен қатар t жиынында r(t)∈Cn,n=2 , онда M0 нүктесі маңайындағы t0 мәндері үшін L қисығы регулярлы. Солай болса келесі шарттар r(t)∈Cn,n=2 және r'(t0)!=0 локальды регулярлы қисықтың шарттары деп аталады.
Қисық доғасының ұзындығы.
Анықтама мен маңызды қасиеттері.
L-жай қисық дейік, оның радиус векторы r=r(t) α=t=β.
α,β сегментін келесі бөліктерге бөлейік
α=t0t1...tn-1tn=β.
L қисығындағы Mi нүктелерін ti мәндеріне сәйкес келетіндей етіп белгілейміз және L қисығын іштей керетін M0M1... Mn-1Mn сызықтарын тұрғызамыз (сурет ).

12 сурет L қисығын іштей 13 сурет L қисығын іштей
керетін M0M1... Mn-1Mn керетін дұрыс сынықтар.
сынықтары
Анықтама. L қисығы түзетілетін деп аталады, егер жай L қисығына іштей керілген сынықтардың ұзындықтарының жиыны шектеулі болса. Бұл жиынның ең жоғарғы дәл қырын L қисығының доғасының ұзындығы деп атаймыз.
Қисық доғасының ұзындықтарының қасиеттері.
Егер L' жай қисығы түзетілген L қисығының бөлігі болса, онда L' қисығы да түзетіледі.
Егер L жай қисығы N нүктесі арқылы түзетілетін L' және L'' бөліктеріне түзетілетін болса, онда L қисығы түзетіледі L" L' және L доғаларының sL' ,s(L") және s(L) ұзындықтары үшін келесі қатынас орындалады.
sL'+s(L")=s(L).
L қисығына кетіретін кез келген сынық түзуді қарастырайық (сурет 14). Оның ең жоғарғы нүктесін N деп белгілеп алайық. Нәтижесінде жаңа сынық түзу аламыз. Оның ұзындығы бастапқы сынық түзуден үлкен және L' және L" қисықтарына кетіретін сынық түзулердің ұзындықтар қосындысына тең болады. Сондықтан L қисығына іштей кетіретін сынықтардың ұзындықтарының жиыны жоғарғы жақтан sL'+s(L") санымен шектелген. Олай болса келесі теңдік орындалады sL=sL'+s(L").

A және B - L қисығында шеткі нүктелер, M- α,β сегментіне жататын t - ның қандайда бір мәніне сәйкес келетін L қисығының нүктесі , ψt,φt,χ(t) - r(t) векторлық функциясының координатасы.
s(t) арқылы AM доғасының ұзындығын белгілейік (сурет 15).
s(t) функциясы қатаң монотомды және α,β сегментінде үзіліссіз және tα болғанда оң.
s(t) ұзындыңының оң екендігі түснікті, ал оның монотомдығы екінші қасиетінен шығады. Енді оның үзіліссіз екенін дәлелдейік.
а) Қандай да ε оң санын алайық . Доғаның ұзындық анықтамасынан белгілі L L ε2 M AM s(t) ε2 ε2 ε2 ψt,φt,χt r(t) L α,β
ε0 α,β ti-1,ti, i=1,2,...,n, δ ψt,φt,χt ti-1,ti
ε(23) ε2
φti-φ(ti-1)2+ψti-ψ(ti-1)2+χti-χ(ti- 1)2ε2.
ε2 ε2 s(t) ε0 α,β
L қисығындағы M нүктесі t=tk мәніне сәйкес болсын. δ арқылы tk-1,t,t,tk+1 сегменттінің ең кіші ұзындығын белгілейік. Егер 0∆tδ болса, онда s(t)s(t+∆t)s(tk+1) орындалады. Бұдан шығатыны келесі теңсіздік.
0st+∆t-ststk+1-s(t)ε
-δ∆t0 теңсіздігі үшін тура солай қарастырамыз. Олай болса
∆tδ үшін келесі теңсіздік барлық кезде орындалады

st+∆t-stε
Олай болса, M нүктесін L қисығының кез келген жерінен таңдағандықтан , α,β сегментіндегі s(t) функциясының үзіліссіздігі дәлелденді. S- L қисығының ұзындығы. s=s(t) функциясы α,β сегментінде 0-ден S -ке дейін қатаң түрде өсетіндіктен және үзіліссіз болғандықтан [0, S] сегментінде үзіліссіз және қатаң өсетін t=t(s) функциясы табылады. Бұдан шығатыны t параметрінің қисықтағы түзелетін s доғасының ұзындығының монотомды жіне үзілссіз функция екенін көрсетеді.
Түзетілудің жеткілікті шарты.
3 ТЕОРЕМА . L қандайда rt=φti+ψtj+χtk, α=t=β векторлық функциясымен берілген жай қисық болсын. Онда егер ψ't,φ't,χ't функциялары α,β сегментінде үзіліссіз болса, онда L қисығы түзетіледі және оның ұзындығы келесі формуламен есептелінеді
S=αβφ'2t+ψ'2t+χ'2(t)dt=αβr'(t)dt.
L(D) L қисығына іштей керілетін сынықтың ұзындығы болсын. Бұл α,βсегментін D бойынша ti-1,ti бөлшектеуге жауап береді. Және бұл сегменттер келесі түрде бөлшектеніп шектелген α=t0t1...tn-1tn=β. Бұл жағдайда L(D) ұзындығы келесі формуламен есептелінеді
lD=i=1nφti-φ(ti-1)2+ψti-ψ(ti-1)2+χt i-χ(ti-1)2=
=i=1nφ'2t'i+ψ'2t"i+χ'2t'''i∆ti,(2)
Мұндағы t'i, t"i, t'''i∈ti-1,ti, ∆ti=ti-ti-1.
ψ't,φ't,χ't функциялары α,β сегментінде үзіліссіз болғандықтан олар абсолютті шама бойынша қандайда бір C тұрақтысымен шектеледі.(2) формуладан келесі теңсіздіктің орындалатыны шығады
0lDC3(β-α)
Яғни L қисығына іштей кетірелін сынықтардың ұзындықтарының жиыны шектелген . Олай болса L -түзелетін қисық . енді (1) формуланың дұрыстығын дәлелдейік. Ол үшін формуладағы интегралдарды келесі түрде алдын ала келесі түрде жазып алайық. Яғни,
αβr'(t)dt=αβφ'2t+ψ'2t+χ'2(t)dt=
i=1nti-1tiφ'2t+ψ'2t+χ'2(t)dt=
i=1nφ'2ti+ψ'2ti+χ'2(ti)∆ti (3)
Мұндағы ti ∈ti-1,ti .
αβr'(t)dt интегралын және l(D) сынығының ұзындығын салыстырайық. (2) және (3) қатынастардан және келесі теңсіздікті пайдалатып
a12+...+an2-b12+...bn2=a1-b1+...+a n-bn
келесі тенсіздіктерді аламыз
αβr'(t)dt-l(D)=
=i=1nφ'2ti+ψ'2ti+χ'2(ti)-φ'2t'i+ψ' 2t"i+χ'2(t'''i)∆ti=
=i=1nφ'ti-φ'(t'i)+ψ'ti-ψ'(t"i)+χ't i-χ'(t'''i)∆ti.
ε0 саны берілсін дейік .Бірқалыпты үзіліссіз ψ't,φ't,χ't функцияларының қасиеттері бойынша соңғы қатынастан
α,β сегментінің барлық бөлшектері үшін келесі теңсіздік орындалады.

αβr'(t)dt-l(D)=ε.(4)
S - lD жиынының ең жоғарғы қыры болса, онда lD ұзындықтардың ішінен(4) және келесі теңсіздікті
0=S-lDε (5)
қанағаттандыратын ең кіші бөлшек табылады. (1) теңдік (4) және (5) қатынастардан шығады және ол кез келген ε үшін орындалады.
1 салдар. 3 теореманың шарттары орындалсын дейік және t - α,β сегменттінің кез келген нүктесі. Онда AM доғасының ұзындығы келесі формуламен анықталады
st=αβr'(τ)dτ (6)
2 салдар. r'(t)!=0 болсын дейік. Онда s=s(t) функциясы кері t=t(s) функциясы табылады және ол r(t) функциясы қанша рет дифференциалданса олда сонша рет дифференциалданады.
*Бұл кері функцияларды дифференциалдану ережесінен шығады. Мысалы, оның 1-ші туындысы
dtds=1dsdt=1r'(t)
r't 1-ші туындысы арқылы өрнектеледі, ал екінші туындысы d2tds2 -
r't r''t арқылы өрнектеледі және сол сияқты кете береді.
Олай болса ,егер L- Ck класының регулярлы қисығы десек онда s табиғи параметріне көшу кезінде ол Ck классының регулярлы қисық болып қала береді.
Ескерту. Егер қисық доғасының ұзындығы параметр ретінде қабылданса ,яғни t=s десек, онда r'(s)=1 (r'2s=1) және r"(s) векторы r'(s) векторына ортогональ.
Оны қарастырып отырған жағдайдан көруге болады,яғни

dsdt=dsds=r'(s)=1.
r'2s=1 теңдігін дифференциалдай отырып, келесі скалыр көбейтіндіні аламыз r"(s) r'(s)=0 . Ол скаляр көбейтінді 0-ге тең болғандықтан r'(s)r"(s) векторларының ортогональды екендігі дәлелденеді.
y=fx,a=x=b тегіс функциясының доғасының ұзындығын анықтайтын формуланы келтірейік
S=ab1+f'2(x)dx.
Доғаның дифференциалы.
(6) формуладағы интегралды жоғарғы шегі t бойынша дифференциалдап, келесі теңдікті аламыз .
s't=r'(t)=φ'2t+ψ'2t+χ'2(t).

Осыдан келесі теңдіктерді
s'tdt=ds, φ'tdt=dφ, ψ'tdt=dψ, χ'tdt=dχ,
ескере отырып,доғаның дифференциалдық формуласына көше аламыз
ds2=dx2+dy2+dz2.
Жанасатын жазықтықтың анықтамасы.
АНЫҚТАМА. L қисығына жанама М0Т арқылы өтетін, -ғы айнымалы жазықтығы ұмтылатын шекті L қисығына М0 арқылы өтетін жанама жазықтық деп атаймыз. (егер PI және жазықтықтары арасындағы θ бұрыш нөлге ұмтылса, онда М0Т түзуі мен М нүктесі арқылы өтетін айнымалы жазықтығы - ғы PI жазықтығының шегі деп аталады) [1].

11 сурет.

Ескерту . Егер PI жазықтығы M--M0 шектік PIMжазықтығында айнымалы, M0 нүктесі арқылы өтетін нормаль PI жазықтығына норма шегі болып PIM жазықтарына M0 нүктесі арқылы өтеді.Дұрыс және кері: егер норма шегі бар болса және айнымалы жазықтықта ,онда жазықтықтың шегі бар болады.

Жанама жазықтықтың бар болуының жеткілікті шарты.
ТЕОРЕМА. - L қисығының радиус векторы және М0 параметрінің мәніне жауап беретін L қисығының нүктесі болсын. Сонда, егер және векторлары коллинеар емес болса, онда М нүктесінде L қисығымен жанасатын жазықтық бар болады, сонымен қатар - осы жазықтыққа жүргізілген нормаль вектор [2,3].
Мұнда , вектор
NPIM=2∆t2r'(t0)xrt0+∆t-rt0
нормалары айнымалы жазықтықта PIM өзімен M--M0 векторлық шегі R'(t0)xr''(t0)!=0.Шектік векторлар және векторлық нормалар PI жанасушы жазықтығына алдыңғы ескертуді қолдандық.
PIM жазықтығындағы NPIM нормасын түрлендірейік.Тейлор формуласын қолданамыз
rt0+∆t-rt0=r't0∆t+12r''(r'').
Сондықтан
r't0xrt0+∆t-rt0=12∆t2r't0xr''t0+α∆t , (1)
Мұнда α(∆t)--0 онда ∆t--0.
Қатынасты екі бөлікке бөлейік 1 , 12∆t2 .Шекті қолданып одан ∆t--0 т.б. M--M0 аламыз ,сосын
NPIM=r't0xr''t0+α∆t∆t--0r't0xr''t0 .
Ескерту .Жанасушы жазықтыққа механикалық ой саламыз .Алдыңғы тарауда біз айтамыз,парметрлік тапсырма L қисығының интерпретациялануы механикалық қозғалыстың нүктедегі заңдылығын Lтроекториясында .Онда r't- нүктенің қозғалыстағы жылдамдығы , r''t-вектор және жылдамдығы.Бұл екі вектор жанасушы жазықтықта жатыр.Жанасушы жазықтықтың анықтамасына сәйкес параметрлік таңдау тәуелсіз ,бұл жазықтықты жазықтың жылдамдығы деп қарастыруға болады , қозғалыстың кез келген заңдылығында L қисығы және вектор жылдамдығы r''t бір жазықтықта жатыр жанасушы жазықтықтың L қисығы M(t) нүктесінде.
Берілген R- вектор туындалған нүктелері PI жанасушы жазықтығында.Сонда вектор R-rt0,r't0,r''t0, M(t0) нүктесінде PI жанасушы жазықтықта орналасқан.Сондықтан, әртүрлі туындысы нөлге тең болады:
R-rt0,r't0,r''t0=0. (2)
(2) формула жанасушы жазық теңдеуі L қисығы M0нүктесінде.
(2) теңдеуді координаталармен жазайық .
Егер x,y,z-R вектор координаталары ,ал φt,ψt,χt-rt векторының координаталары, (2) қатынaс былай жазылады:
x-φ(t0)y-ψ(t0)z-χ(t0)φ'(t0)ψ'(t0)χ' (t0)φ''(t0)ψ''(t0)χ''(t0)=0

Жанама жазықтықтың бар болуының жеткілікті шарты.
ТЕОРЕМА. - L қисығының радиус векторы және М0 параметрінің мәніне жауап беретін L қисығының нүктесі болсын. Сонда, егер және векторлары коллинеар емес болса, онда М нүктесінде L қисығымен жанасатын жазықтық бар болады, сонымен қатар - осы жазықтыққа жүргізілген нормаль вектор [1,2].
Қисықтың бас нормальі мен бинормальі.
L қисығының М нүктесіндегі жанамаға перпендикуляр болып, L қисығының М нүктесі арқылы кез келген түзу L қисығының М нүктесіндегі нормаль қисығы деп аталады.
L қисығының М нүктесінен өтетін жанама жазықтықта орналасқан нормаль негізгі нормаль , ал осы жанама жазықтыққа перпендикуляр нормаль бинормаль деп аталады [1].
Жанасушы басты норма және қисықтың бинормалі бұл нүктеде қисық үш жазықтықты анықтайды және сол нүктемен қисыққа байланысты.Осы жазықтықта бізге таныс жанасушы жазық бар.Ол жанама мен басты норма арқылы өтеді.Басты норма мен бинорма арқылы өтетін жазықтық нормаланған жазық деп аталады (ол бүкіл норма мен қисықты бір нүктеде ұстайды).Жанама және бинормаль арқылы өтетін жазықтық түзетуші жазықтық деп аталады.

12 сурет.
Бұл үш жазықтық жанасушы,нормаланған және түзетуші негізгі триэдр қисығын анықтайды.
τ,n,b- бірлік үштігі ортогональды векторға теңдей,M нүктесінің өлшемі және жанамаға қатысты ,басты норма және бинорма. Бұл векторларды бағдарлау келесі түрде таңдалады:τ векторы r' векторына бағыттас,n векторының соңы сол жазықтықта жанасушы жазықта,r'' векторында көрсетіледі.b векторы таңдалады былай, τ,n,b үштіктің дұрыстығында.
Сонымен,τ,n,n векторларының бағыттас векторлар қарастырамыз.

Қисықтың қисықтығы.
- дағы қатынастың шегін L қисығының М нүктесіндегі қисықтығы деп атайды, мұндағы Θ - L қисығының М және М0 нүктелеріне жүргізілген жанамалардың арасындағы бұрыш, ал Δs - М0М доғасының ұзындығы [3].

13 сурет.
Кейде k1 - ді қисықтың бірінші қисықтығы деп атайды.
Теорема.Берілсін rt- вектор қисығы L және M0- нүктесі L қисығында,t0 параметріне жауап беретін.Онда,егер r't0!=0 және r''t0 бар болсын L қисығы M0 нүктесінде k1 қисығында.Егер параметр -s доғаның ұзындығы,онда
k1s0=r''(s0). (1)
Кез келген параметрлеу
k1t0=r'(t0)xr''(t0)r'(t0)3 . (2)
Берілген параметр -s доғаның ұзындығы.Сонда
r's0+∆s-r'(s0)=2sinΘ2.
Осыдан аламыз,
r's0+∆s-r'(s0)Δs=sinΘ2Θ2*ΘΔs.
Соңғы теңдікке M--M0 шегіне көшейік.∆s--0 және Θ--0 ,сол шегі бөлімде бар және r''(s0) тең.Онда, шек және оң жағында R1(s0) бар болады.Осындай түрмен,L қисығы M0 нүктесінде қисықтығы бар,және (1) формаула ерекше.
Есімізге түсіре келе,
dsdt=r'(t)=r'2(t)
кез келген параметрлеуде өзімізбен
r'=drdt=drds*dsdt=drds*r'2.
дифференциялдап r' тағыда t , біз аламыз
r''=d2rds2*r'2+drds*r',r''r'2.
Екі бөліктіде соңғы теңдікте квадраттаймыз.
Ортогональды векторлар drds және d2rds2 және теңдеу
d2rds22=k12, drds2=1 ,
қатынасқа келеміз
r''2=k12(r'2)2+r',r''2r'2,
k12=r'2*r''2-r',r''2r'23=r'xr''2r'6 .
Осыдан квадраттын түбірін тапқан соң (2) формуланы аламыз.
Ескерту 1.Егер r' және r'' векторлары коллинарлы емес,(1) және (2) формулада, k1!=0 және керісінше ,егер k1!=0 ,r' және r'' векторларыда коллинарлы емес.
Жазық қисықтың қисықтығы,параметрлік теңдеумен берілген x=xt,y=yt,мына формуламен есептейміз
k1=x'y''-x''y'x'2+y'232.
Қисықтың y=fx функциясының графигі мына формуламен табылады
k1=f''x'2+y'232.
Ескерту 2 .Кейде жазықтың қисықтығы былай беріледі.Әдетте оны жанаманы қисыққа Ox осі қатынасына : егер бұл сағат тіліне қарама қарсы болса k10,егер сағат тіліне бағыттас болса k10 .Сонымен мұндай белгі қисықтың қисықтығы-y=f(x) функциясының графигінде-f'' екінші туындысымен дәл келеді.Сонымен
k1=f''1+f'232.

Есептеулерге байланысты көрсетуге болады,түзудің қисықтығы нөлге тең,шеңбердің R радиусы 1R тең.
Дұрыс және кері: егер қисықтың қисықтығы нөлге тең,онда қисықтың көптеген түзулермен байланысты,ал егер қисық түзуің қисықтығы a тұрақтыға тең,ал бұл қисық доға шеңбердің радиусы 1a тең.
Қисық бұрышы.
L қисығын қарастырамыз және оның нүктелері M0s0 және M(s0+∆s).БерілсінΘ- жанасушы жазықтың арасындағы бұрыш.PI0 және PI қисығы M0 және M нүктелеріне қатысты.Бұдан көруге болады,бинормалдың арасындағы бұрыш b0=b0(s0 ) жәнеb=bs0+Δs ,M0 және M нүктелері Θ тең болады [5,6].
Біз шекті қарастырамыз
limM--M0ΘΔs.
Түсінікті, бинорманы айналдырғанда s параметрі үлкейген вектордың басты нормасы bs және n(s) векторларын кері жорысақ коллинеар екенін дәлелдейік.
Бұл шама
limM--M0ΘΔs.
белгіленеді.
Белгілердің таңдау ережесі қатынасқа байланысты.Біз келесі белгілердің таңдау ережесін қолданамыз:егер b's және n(s) векторлары бағыттас болса,онда мұны шектің теріс деп есептейміз,ал егер b 's және n(s) векторлары қарама-қарсы бағытта болса,- оң деп есептейміз.

Қисықтың ширатылуы.
L қисығының М нүктесіндегі ширатылуы деп, таңбаларды таңдау ержесіне сәйкес бекітілген шекті айтамыз.
Кейде - ні қисықтың екінші қисықтығы деп атайды.
Теорема 6.Берілсін rt векторы L қисығында және M0 нүктесінде.t0 параметрі мағынасына жауап беретін.Онда r't0 және r'' t0 векторлары коллинеар емес,r'''t0 векторы табылады,L қисығы M0 нүктесінде k2t0 бұрылымы бар.Егер параметр-s доға ұзындығы,
k2s0=r's0,r''s0,r'''(s0)r''2(s0). (3)
Кез келген параметрлеу
k2t0=r't0,r''t0,r'''(t0)r'(t0)xr''( t0)2. (4)
Берілген параметр-s доға ұзындығы.r's0 және r''(s0) векторлары коллинеарлы емес,және M нүктесінің кейбір маңайында.M нүктесін алайық,L қисығында сол маңайдан.Теорема 4 сай M және M0 нүктелерінде жанасушы жазық қисығы бар,және бинормалы b0=bs0 жәнеb=b(s0+∆s).Осыдан аламыз
bs0+∆s-b(s0)∆s=sinΘ2Θ2*ΘΔs.
Сонымен M--M0 және ∆s--0 және Θ--0 .Сондықтан сол шегі соңғы теңдеудің өзімен бірге b'(s0) тең болады.Тағыда оң шегінің мағынасы бар болады,осы бөлікте.Бізге қиын емес ,бұл k2(s0) тең екені.
Осындай тәсілмен,
b'(s0)=k2(s0). (5)
Жоғарғы,белгілердің таңдаудағы ережесі , біз коллинеарлы векторларды b'(s0) және ns0 қолдандық.Дәлелдейміз, b'(s0) және ns0 векторлары әрқашан коллинеарлы.Бұл үшін бізге b'(s0) векторының bs0 және τ(s0) векторларында ортогональ екені( n=bxτ, ескереміз) . b'(s0) векторы bs0 векторында ортогональ,осыдан шығады b2=1 теңдігі,одан b',b=0.
Көрсетеміз, b'(s0) векторы τ(s0) векторына ортогональ екенін. r'(s0) векторы- бірлік және жанамаға бағыттас ,онда r's0=τs0. r''s0 векторы r'(s0) векторына ортогональ және жанасушы жазықта жатыр.Сонымен қатар τ's0=r''s0 векторы коллинеарлы n(s0) векторына, τ's0xns0=Ο .
b=τxn теңдеуінің туындысын тауып,b'=τxn' теңдігін аламыз.Осындай тәсілмен b's0 векторы τs0 векторына ортогональ.Сонымен,b' және n векторлары коллинеарлы.Осыдан (5) формуланы қолданып,b'=-k2n және
k2=-b',n
(6) формуланы қорытып шығамыз.
(6) формуланы қолданып n және b' векторларының мағынасы:
n=r''r''2,
b'=τxn'=r'xr''r''2'=r'xr'''r''2+r'x r''1r''2,
Осыдан аламыз
k2=r',r'',r'''r''2.
Осындай тәсілмен ,қисығы нүктесінде бұрылым бар,формула ерекше.
Френе формуласы.
ТЕОРЕМА. L - С3 - жүйелі қисық, L қисықтың доға ұзындығы - s, негізгі триэдрдің векторлары , L қисықтың қисықтығы мен ширатылуы - болсын. Сонда келесі теңдіктер дұрыс болады:

Бұл қатынастар Френе формуласы деп аталады .
τ=r's,τ'=r"(s) болғандықтан және r" векторы n векторымен бағыттас, сондай ақ r"=k1 болса, онда τ'=k1n . Френе 1-ші формуласы дәлелденді.
3-ші формуласы 6 теореманы дәлелдеу кезінде дәлелденген.
2-ші формуланы негіздеу үшін n=bxτ теңдігін дефференциалдаймыз. Нәтижесінде келесі теңдікті аламыз
n'=b'xτ+bxτ'=-k2nxτ+k1bxn=-k1τ+k2b.
Берілген нүктеге жақын қисықтың түрі.
Ол үшін L қисығынығ M0 нүктесін координаттар басын беттестіреміз. Олай болса rs0=0 . Онда жіктелу центрі s0=0 нүктесінде болатын Тейлор формуласы бойынша жіктесек ,келесі формуланы аламыз
rs=r'0s+12r"(0)s2+16r'''(0)s3+0(s3) (8).
Бұл формуланың оң жағын s0=0 нүкесінде алынған τ n,b векторларын пайдалана отырып, түрлендірейік. r'0=τ,r"(0)=τ'=k1n, r'''(0)=k1n-k12τ+k1k2b болса, онда осы өрнектерді (8) формулаға койып келесі формуланы аламыз
rs=s-k136s3τ+k12s2+k'16s3n+k1k26s3b +0s3 (9)

Соңғы формуланы пайдаланып ,берілген M0 нүктесіне жақын L қисығының түрін жаза аламыз (21 сурет).

Oxyz τ,n,b Ox,Oy,Oz
L L M0
x=s,y=k12s2-y=k12x2 L
y=k12s2,z=k1k26s3-z2=αy3 L Oxz
x=z,z=k1k26s3-z=k1k26x3

Табиғи қисық теңдеуі.
ТЕОРЕМА. Үзіліссіз туынды k1(s)0 және k2(s) функциялары [0,S] берілсін. Онда С3 - регулярлы қисық , s∈[0,S] қисықтың доға ұзындығына тең тиісінше болады .
Френе формуласын қарастырамыз:

τs,ns,b(s) белгісіз функциялар үшін қарапайым дифференциалдық теңдеулер жүйесі ретінде берілген.
Бастапқыда берілген жүйе үшін сәйкесінше ортогоналды векторларды τ0,n0,b0 таңдап алып, біріңғай қалыптастырамыз:
τ0,n0,b0=1, τ02=1, n02=1, b02=1, (τ0,n0)=0,
τ0,b0=0, n0,b0=0.
Каши есептерінің шешімдерінің жалғыз және бар болуы теоремасына сәйкесқарапайым дифференциальдық теңдеулері үшін [0,S] сегментә кезінде C1 классында (7) жүйенің жалғыз шешімдері τs,ns,b(s) табылады және олар алғашқы шарттарды қанағаттандырады.
τ0=τ0, n0=n0, b0=b0.

Сурет 24. Кубтық параболаға жақындайтын Сурет25 .Винтік сызық
түзетілетін жазықтығына проекциеленетін
қисық
Мысалы: қисықтық және бұралу табу
rt=acost, asint, bt
Сонымен
r'2=a2+b2, (r'xr'')2=a2a2+b2, r',r'',r'''=a2b,
Онда
k1=aa2+b2, k2=ba2+b2,
Яғни винттік қисықтың қисықтығы және бұралуы тұрақты. Мұндай қасиет тек винттік қисықтарға тән.
Қисықтардың жанасуы.
Жанасу реті туралы ұғым.
Ортақ M0 нүктесі , арқылы өтетін және ортақ M0Т жанамасы бар , L1 және L2 қисықтарын қарастырайық. M0Т түзуінің M0 нүктесіне жақын P нүктесін алайық және осы P нүктесі арқылы M0Т түзуіне перпендикуляр PI жазықтығын жүргізейік . Бұл жазықтық L1 және L2 қисықтарын сәйкесінше М1 және М2 нүктелерінде қисын. l арқылы M0Р кесіндісін ,ал һ арқылы М1М2 кесіндісін белгілейік.

Анықтама. L1 және L2 қисықтарының M0 нүктесіндегі жанасу реті q∈N санынан төмен түспейді, егер
liml--0hlq=0 (*)
Сонымен қатар,
liml--0hlq+1!=0 (**)
Болып hlq+1 қатынасы l--0 шегі болмаса, онда L1 және L2 қисықтарының M0 жанасу реті q ге теге тең . Егер (1) - ші теңдеу кез - келген q∈N үшін орындалса, онда L1 және L2 қисықтары M0 нүктесінде шексіз реті жанасуы болады.
1-ші мысал. L1- Ох осі болсын, ал L2- қисығы екелесі функция
y=fx=e-1x, x!=0,0, x=0.
L1 және L2 қисықтарының координата басында шексіз жанасуда болатынын көрсетейік.
Қарастырылып отырған жағдайда l=x, h=e-1x .Сондай ақ q∈N үшін
liml--0hlq=limx--0e-1xxq=0,
Онда біздің ұйғарымымыз дұрыс.
2-ші мысал. L1 және L2 y=x2 және y=3x2 функцияларының графиктері дейік. L1 және L2 қисықтары x=0, y=0 нүктесінде бір ортақ жанасуға ие. Дәлелдеп көрейік, бұл жағдайда l=x, h=2x2. Онда
liml--0hl=limx--02x2x=0 , liml--0hl2=limx--02x2x2=2!=0
Олай болса, L1 және L2 қисықтарының (0,0) нүктесінде жанасу реті 1-ге тең.
3-ші мысал. L1-Ox осі болсын, ал L2 қисығы келесі параметрләк теңдеулермен берілсін x=t,y=t37,2, z=t90.
L1 және L2 қисықтарының координаттар басындағы жанасуының ретін анықтайық
l=t, h=t74,4+t180=t37,2∙1+t105,8.
liml--0hl37=limt--0t0,2∙1+t15,8=0
hl37+1 қатынасының шегі болмайтындықьан (шегі теңсіздікке ұмтылады) , L1 және L2 қисықтарының жанасу реті (0,0) нүктесінде 37-ге тең.

Жанасатын шеңберлер.
L- қандайда M0 нүктесінің айналасындағы регулярлы қисық дейік. Осы қисықтың M0 нүстесінде жанасатын шеңберлерді қарастырайық. Осы жанасатын шеңбердің L қисығымен жанасу реті екіден кем емес болса, онда оларды жанасатын шеңберлер деп атайды .

Теорема. Егер L регулярлы қисығының M0 нүктесіндегі қисықтығы k1 нольге тең болса, онда бұл нүктеде L қисығына жанасатын шеңбер жүргізуге болады. бұл шеңбер L қисығының жанасу жазықтығында жатады және оның радиусы R=1k1M0.
Ескерту 1. Егер k1M0=0 болса, онда L қисығының қисықтығы M0 нүктесінде нольге тең. бұл жағдайда жанасатын шеңбер L қисығының M0 нүктесінде түзу сызыққа айналады.
Ескерту 2. L- c2 регулярлы қисық дейік және оның қисықтығы k1 нольге тең емес болсын. Егер r(t) L қисығының радиус векторы десек, онда қисықтың M0 нүктесіндегі жанасу шеңберінің центрі келесі векторлық қатынаспен анықталады, яғни
rц=rt+1k1(M)n, (*)
Мұндағы n L қисығының М нүктесіндегі басты нормаль векторы центр және жанасатын шеңбердің радиусы сәйкесінше центр және қисықтың қисықтығының радиусы деп аталады. Қисықтың қисықтығы радиусы келесі формуламен анықталады R=1k1.
Жазық қисықтардың эволютасы және эвольвентасы.
L- c2 регулярлы жазықтықтағы қисық дейік және оның k1(M) қисықтығы М нүктесінің кез келгенінде нольге тең емес .
Анықтама. L қисығының эволютасы деп оның қисықтығының центрлерінің жиынын айтамыз.
Ал, эволютаға қарағандағы L қисығының өзін эвольвента деп атайды.

Егер rt-L қисығының векторы, ал k1 қисықтың қисықтығы десек, онда (*) формуласына сәйкес оның эволютасы келесі формуламен анықталады
rц=rt+1k1(M)n (**),
Мұндағы n-L қисығының бас нормаль векторы.
Мысалы. Эллипстің эволютасын табыңыз.
rt=acost,bsint, 0=t2PI-эллипстің векторы, ab.
Осы векторды (**) формуласына қойып, келесі векторды аламыз.
rцt=a2-b2acos3t, b2-a2bsin3t
Эллипстің эвлоютасы ұзартылған астронда қисығы.

Жаттығулар
1. Астроид доғасының ұзындығын табыңыз
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.