Тік бұрышты үшбұрыштар: тригонометриялық функциялар, Пифагор, синус және косинустар теоремалары


Жоспар
- Tiк бұрышты үшбұрыштың бұрыштары мен кабырғаларының арасындағы қатынастар (8 сынып) Сүйір бұрыштың тригонометриялық функцияларыПифагор теңбе-теңдіктерТікбұрышты үшбұрыштарды шешуТік және доғал үшбұрыштарды шешуҚашықтықтар мен бұрыштарды табуға арналған практикалық есептер
- Үшбырыштарды шешу (9 сынып) Синустар теоремасыКосинустар теоремасыШеңберге іштей сызылған бұрыштарШеңберде берілген бұрыштарШеңбер мен байланысқан кесінділер
СОӨЖ 1 . Кеңес беру және СӨЖ 1 қабылдау
СӨЖ 1
- «Планиметрия аксиомалары» бойынша эссе жазу.
- Пифагор, косинустар, синустар теоремаларына эссе жазу.
3. «Үшбұрыштар тақырыбына» ең кемі 7 есеп шығару
Әдебиеттер тізімі
- Смирнов В. А., Тұяқов Е. А. Геометрия. 8-сынып. Оқулық. /Оқу құралдары: Әдістемелікнұсқау. Дидактикалық материалдар. Есептер жинағы. / - Алматы: Мектеп, 2018. - 160 б . . .
- Смирнов В. А., Тұяқов Е. А. Геометрия. 9-сынып. Оқулық. /Оқу құралдары: Әдістемелік нұсқау. Дидактикалық материалдар. Есептер жинағы. /- Алматы: Мектеп, 2019. - 184 б . . . Сүйір бұрыштың тригонометриялық функциялары
Тікбұрышты үшбұрыштың сүйір бұрышының синусы деп осы бұрышқа қарсы жатқан катеттің гипотенузаға қатынасын айтады. В
А бұрышының синусы sinA арқылы белгіленеді:
А С
Тікбұрышты үшбұрыштың сүйір бұрышының косинусы
деп осы бұрышқа іргелес жатқан катеттің гипотенузаға қатынасын айтады.
А бұрышының косинусы cosA арқылы белгіленеді:
Тікбұрышты үшбұрыштың сүйір бұрышының тангенсы деп осы бұрышқа қарсы жатқан катеттің іргелес жатқан катетке қатынасын айтады.
А бұрышының тангенсі tgA арқылы белгіленеді:
Тікбұрышты үшбұрыштың сүйір бұрышының катангенсы деп осы бұрышқа іргелес жатқан катеттің қарсы жатқан катетке қатынасын айтады.
А бұрышының катангенсы сtgA арқылы белгіленеді:
.
Осы анықтамалардан келесі теңдіктер шығады:
.
Синус, косинус, тангенс және котангесті сүйір бұрыштың тригонометриялық функциялары деп атайды.
Тригонометриялық функциялардың кейбір бұрыштардағы мәндері: sin30 0 = cos60 0 = tg45 0 =1, ctg45 0 =1.
sin45 0 = cos45 0 0. 71, sin60 0 = cos30 0 0. 87,
tg30 0 = ctg60 0 0. 58 tg60 0 = ctg30 0 1. 73.
- Пифагор теоремасы
Ұлы ғалым Пифагор б. з. д. 580 жылы Самос аралында туған. Пифагордың әкесі Мнесарх зергер болған. Пифагордың анасының аты белгісіз. Көптеген жазбалар бойынша туған бала өте әдемі болған және өсе келе өзінің ерекше қабілетімен көзге түскен.
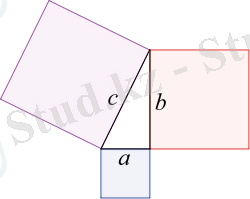
Пифагор теоремасы - тік бұрышты үшбұрыштың қабырғаларының арасындағы байланысты тұжырымдайтын геометрия теоремасы. Пифагор теогремасы Пифагорға дейін де белгілі болған, бірақ оны жалпы түрде дәлелдеген Пифагор. Алғашында теорема тік бұрышты үшбұрыштың гипотенузасы мен катеттеріне салынған квадраттар аудандарының қатынасын тұжырымдаған: гипотенузаға тұрғызылған квадрат ауданы катеттерге тұрғызылған квадраттар аудандарының қосындысына тең.
Пифагор теоремасы қысқаша былай тұжырымдалады: тік бұрышты үшбұрыштың гипотенузасының квадраты катеттері квадраттарының қосындысына тең.
Пифагор теоремасына төмендегідей кері теорема да дұрыс: егер үшбұрыштың бір қабырғасы ұзындығының квадраты қалған екі қабырғасы ұзындықтарының квадратына тең болса, онда ол үшбұрыш тік бұрышты болады.
Бекіту сұрақтары
1. Пифагор теоремасы қандай үшбұрыш үшін орындалады ?
2. Ұзындықтары 5, 4, 3-ке тең кесінділер тік бұрышты үшбұрыштың қабырғалары болады деп есептеуге бола ма?
3. Қабырғаларының ұзындықтары 5, 6, 7 болатын үшбұрыш тік бұрышты ма?
4. Пифагор теоремасын тағы да қандай фигуралар үшін қолдануға болады?
1. 3 Негізгі тригонометриялық теңбе-теңдіктер
α сүйір бұрышының әрбір мәніне сәйкес sinα-ның, cosα-ның, tgα-ның және ctgα-ның мәндерін анықтауға болады.
1. Катеттері а мен b , гипотенузасы с болатын, ал сүйір бұрыштары α мен β -ға тең АВС тік бұрышты үшбұрышы берілсін. Пифагор теоремасын жазамыз:
a 2 +b 2 =c 2 (*)
Жоғарыдағы формулалардан b=ccosα , a=csinα болатыны белгілі. Осы мәндерді (*) -ға қойсақ,
sin 2 α+cos 2 α=1 (1)
шығады. Бұл α бұрышының синусы мен косинусын байланыстыратын теңбе-теңдік.
2. Берілген тікбұрышты үшбұрыш үшін
болатыны белгілі. Бұл теңдіктерге b=ccosα, a=csinα мәндерін қойсақ,
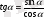 (2)
(2)
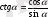 (3)
(3)
аламыз. Бұл теңдіктер кез-келген α сүйір бұрышы үшін орындалатын
теңбе-теңдік болып саналады.
3. (1) тепе-теңдіктің әрбір мүшесін сos 2 α-ға немесе sin 2 α-ға бөліп, төмендегідей екі тепе-теңдікті алуға болады:
1+tg
2
α=
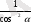 (4)
(4)
1+ctg
2
α=
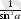 (5)
(5)
4. АВС тікбұрышты үшбұрышына сүйір бұрыштар үшін α+β=90 0 , бұдан β=90 0 -α .
sin β =
 , ал cosβ=
, ал cosβ=
 .
Сонда,
.
Сонда,
sin(90 0 -α) =cosα (6)
теңбе-теңдігін аламыз.
Осы сияқты
cos(90 0 -α) =sinα (7)
теңбе-теңдігін алуға болады.
- Синустар теоремасы
Синустар теоремасы - кез келген үшбұрыштың а, b, с қабырғалары мен оларға қарсы жатқан А, В, С ( , ) бұрыштарының синустары арасындағы қатысты сипаттайтын тригонометриялық теорема.
Теорема. Үшбұрыштың қабырғалары оларға қарсы жатқан бұрыштардың синустарына пропорционал болады.
Формула түрінде мына теңдіктер арқылы жазылады:
a sin α = b sin β = c sin γ = 2 R, {\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R, }
мұндағы aa {\displaystyle a}, b, c c {\displaystyle c} - үшбұрыш қабырғалары, , - сәйкесінше оларға қарсы жатқан төбелеріндегі бұрыштар.
Егер R R {\displaystyle R} - үшбұрышқа сырттай сызылған шеңбер радиусы болса, онда мына теңдіктерде орын алады:
a sin α = b sin β = c sin γ = 2 R . {\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R. }
Дәлелдеу.
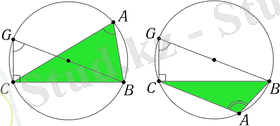
Мынаны дәлелдесе жеткілікті:
a sin α = 2 R . {\displaystyle {\frac {a}{\sin \alpha }}=2R. }
Сырттай сызылған шеңбердің диаметрін B G {\displaystyle BG} жүргізейік. Шеңберге іштей сызылған бұрыштар қаситеі бойынша бұрыш G C B {\displaystyle GCB} GCB тік болады, ал бұрыш C G B {\displaystyle CGB} CGB немесе α {\displaystyle \alpha } (бұрыш CAB C A B {\displaystyle CAB} ), егер A {\displaystyle A} A мен G {\displaystyle G} G нүктелері B C {\displaystyle BC} BC түзуінің бір жағында жатса, π − α {\displaystyle \pi -\alpha } мәніне тең. Кері жағдайда sin π − α {\displaystyle \pi -\alpha } π − α {\displaystyle \pi -\alpha } sin ( π − α ) = sin α {\displaystyle \sin(\pi -\alpha ) =\sin \alpha } болғандықтан, екі жағдайда да a = 2 R sin α {\displaystyle a=2R\sin \alpha } a=2Rsinπ − α {\displaystyle \pi -\alpha } . Осы жолмен басқа екі қабырғалары үшін де табамыз, Сонда:
a sin α = b sin β = c sin γ = 2 R . {\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R. }
Теорема дәлелді: .
Теорема. Үшбұрыштың бұрышының биссектрисасы осы бұрышқа қарсы жатқан қабырғаны оған іргелес жатқан қабырғаларына пропорционал бөліктерге бөледі.
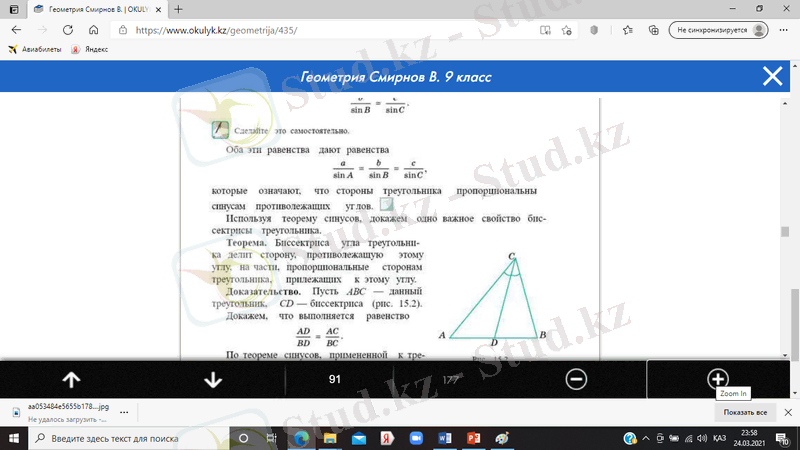
Берілгені: BС=a, AC=b, CD -биссектриса,
AD=m, BD=n.
Дәлелдеу керек:
Дәлелдеу:
( CD -биссектриса)
ендеше ;
m=
(келтіру формуласы бойынша)
n=
, .
- Косинустар теоремасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz