Санның бүтін және бөлшек бөлігінің сирек қолданылатын қасиеттері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІ

Ғылыми жұмыс

Санның бүтін және бөлшек бөлігінің
сирек қолданылатын қасиеттері

Секциясы: Математика
Жоба авторы: Борисова Құндыз Саматқызы
Сыныбы: 11
Ғылыми жетекшісі: Жумашева А.Ж

2021-2022 оқу жылы
Мақат ауданының Бәйге төбе мектеп-бөбекжай кешені
коммуналдық мемлекеттік мекемесінің
11 сынып оқушысы Борисова Құндыздың
Санның бүтін және бөлшек бөлігі атты ғылыми жобасына

П і к і р
Санның бүтін және бөлшек бөлігіне анықтама мектеп бағдарламасында классикалық түрде беріліп, мардымды мысалдар қарастырылады. Бірақ олимпиада есептерінде, конкурстық есептерде осы тақырыпқа мысалдар беріліп тұрады. В.С.Кимнің авторлығымен жазылған Математика для любознательных (с решениями, г. Павлодар, 2010 г.) кітабында №73 есебін шығару барысында толық әрі нақты шешім алынбаған. Осы олқылық толық толтырылған, жалпы жағдай орынды қарастырылған. Республикалық ғылыми-әдістемелік Математика және физика журналының 2004ж №3 санында О.Әжіғалиевтың Санның бүтін бөлігі және оның қолданылуы атты мақаласында жіберілген кемшіліктер түзетілген, жалпы жағдайда шешімін тапқан.
Сонымен қатар, автор санның бүтін және бөлшек бөлігіне қатысты қасиеттерін толығымен жинақтаған. Оны мысалдарды шығару барысында тиімді қолдана алған.
Тақырып шағын көлемде алынған, әйтпесе жұмыстың ауқымы ғылыми жоба жұмысына қойылатын талап көлемінен бірнеше есе асып кеткен болар еді. Теңдеулерді шешіп, одан соң теңсіздіктерді шешуге өту қамтылған.
Барлық мысалдар автор тарапынан құрастырылғандығымен құнды деп есептеймін.
Теориялық қателіктер немесе олқылықтар кездеспеді. Жұмысты әртүрлі деңгейдегі оқушылар арасында өтетін жұмыстарға ғылыми жұмыс ретінде ұсынуға болады.

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3
I. Негізгі бөлім
1.1.Теориялық бөлім ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5
1.2 Теңдеудің құрамында санның тек бүтін бөлігін беретін таңба жалғыз рет кезлдесетін мысалдар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .6
1.3 Практикалық бөлім ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 8
а) Сандардың бүтін және бөлшек бөліктеріне тән қасиеттерді тікелей қолдануға мысалдар қарастыру
б) Теңдеудің құрамында санның тек бөлшек бөлігін беретін таңба жалғыз рет кездесетін мысалдар
в) Теңдеудің құрамында санның бөлшек және бүтін бөлігін беретін таңба бір-бір реттен кездесетін мысалдар.
г) Теңдеудің құрамында санның бүтін бөлігін беретін таңба екі рет кездесетін мысалдар

II.Зерттеу бөлімі
2.1 ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..1 0
III. Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..14
Пайдаланылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... 15

Кіріспе
Санның бүтін және бөлшек бөлігі ұғымы мектеп математика курсына енгізілген және тек нақты сандардың бүтін бөлігін немесе бөлшек бөлігін табумен ғана шектеледі.
Санның бүтін бөлігін [х] таңбасымен, ал бөлшек бөлігін {х} таңбасымен белгілейді. Ең қарапайым көрінісі, кез келген х саны үшін:
У=[х]+ {х}=х (1)
болған координата жазықтығының I және III ширек биссектрисасының теңдеуін береді. (1) теңдеуден мынандай салдарларды аламыз:
[x]=x-{x} және {x}=x-[x] (2)
Мысалы x=7,4 болсын, онда [7,4]=7 болып, {7,4}=7,4-7=0,4 болады.
Осы бір мысалдың өзінен мынаны байқауға болады:
Бүкіл сан түзуінде, егер сан бүтін болса, онда санның бүтін бөлігі санның өзіне тең болады;
Бүкіл сан түзуінде сан аралас сан болса, онда оның бүтін бөлігі сол санның сол жағында жатқан бірінші бүтін сан болады.
х=6,2 [x]=[6,2]=6
x=0,4 [x]=[0,4]=0
х=-5 [x]=[-5]=-5
x=-3,4 [-3,4]=-4.
Осы заңдылықтарды ескеріп мынандай формуланы аламыз,
x-1[a] =x (3)
x=-3,4 болса -3,4-1[-3,4] =-3,4 -4,4-3-3,4
Санның бөлшек бөлігін (2) формуласымен табу қажет болсын.
X=8,03 {x}=x-[x]=8,03-[8,03]=8,03-8=0,030
X=-2,6 {x}=x-[x]=-2,6-[-2,6]=-2,6+3=0,40
X=-0,3 {x}=x-[x]=-0,3-[-0,3]=-0,3+1=0,70
Бұдан барлық кезде {x} = 0 болады, әрі мынандай қос теңсіздік орындалады.
0 ={x}1 (4)
Олимпиадалық, конкурстық т.б сайыстарда санның бүтін және бөлшек бөліктеріне есептер берілетіні ескеріліп, оқырмандарға санның бүтін және бөлшек бөліктері туралы толығырақ мағлұмат беруді жөн көрдік. Осыған орай ғылыми жоба жұмысының теориялық бөлімінде жұмыс барысында қажет болатын саннық бүтін және бөлшек бөліктеріне тән қасиеттері қаралып жинақталды. Құрастырылған есептер арқылы қасиеттердің дұрыстығы бекітіле түседі. Практикалық бөлімде, теориялық бөлімде қарастырылған қасиеттер үнемі қолдануға болады.
Ғылыми жобаның мақсаты.
Мектеп бағдарламасы көлемінде санның бүтін және бөлшек бөлігіне анықтама беріледі, өте мардымсыз мысалдар қарастырылады. Олимпиадалық есептерде осы берілген анықтама негізінде шығарылатын есептер кездесіп тұрады. Сол себепті осы ғылыми жоба жұмысымызда алдымызға мынандай мақсаттар қойдық:
1.Санның бүтін және бөлшек бөлігінде тән қасиеттерді көлемді толықтыра түсу;
2.Алынған қасиеттер арқылы шешуге болатын санның бүтін және бөлшек бөлігіне өрнектерді, теңдеуерді,теңсіздіктерді құрастырып, оларды шешудің әдістемесін қоса беру;
3.Саннның бүтін және бөлшек бөлігіне берілген есептердің ауқымын одан әрі кеңейте түсу;
4.В.С.Кимнің авторлығымен жазылған математика для любознательных (с решениями, г.Павлодар, 2010) кітабындағы №6.73 есебін шығару барысында толық нақты нәтиже алынбаған, осы олқылықты болдырмауды көздеп, санның бүтін және бөлшек бөліктеріне берілген теңдеулерді жалпы жағдайда қарастырып, барлық шешімдерін алу, бөгде шешімдерінен арылу;
5.Республикалық ғылыми-әдістемелік математика және физика журналының 2004ж №3 санында О.Әжіғалиевтің санның бүтін бөлігін және оның қолданылуы атты мақаласында дербес көріністе мысалын жалпы жағдайда толық шешімін беру, тепе-теңдігін дәлелдеу қарастырылған, бірақ өрнегінің басқадай мәндерге ие болатынын көрсету.

I.Негізгі бөлім
1.Теориялық бөлім
Санның бүтін және бөлшек бөлігіне тән қасиеттер
Кез келген санның нақты бөлігі [x] және бөлшек бөлігі{x} болсын , онда санның бүтін және бөлшек бөлігіне тән қасиеттер төмендегідей болады:
1-қасиет. Кез келген нақты сан үшін x=[x]+{x} теңдігі орындалады.
x=-3,5 -3,5=[-3,5]+{3,5}= -4+0,5
2-қасиет. Кез келген нақты х саны үшін [x]=x-{x} және {x}=x-[x] теңдіктері орындалады.
X=5,2 -- [x]=[5,2]=5, {5,2}=0,2 -- [x]=5,2-5, {x}=5,2-0,2
3-қасиет. Кез келген нақты х саны үшін x-1[x]x теңдігі орындалады.
X=-4,3 -4,3-1[-4,3]-4,3 -5,3-5-4,3
4-қасиет. Кез келген нақты х саны үшін [x]=0 болса, 0=x1 болады.
1-мысал. 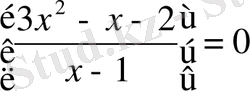-теңдеуін шешіңдер.
Шешуі: 0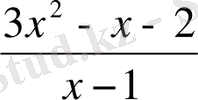=1

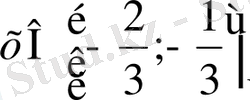
Жауабы:
5-қасиет. Кез келген нақты х саны үшін [x]a болса,онда xa теңсіздігі орындалады.
2-мысал. теңсіздігін шешіңдер
Шешуі:
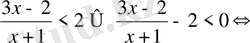
Жауабы: (-1,4)
6-қасиет. Кез келген нақты х саны үшін [x]a болса, онда xa+1 теңсіздігі орындалады.
3-мысал. 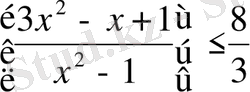теңсіздігін шешіңдер.
Шешуі:

(-infinity;-3,5)(-1;1)(2;infinity)
Жауабы: (-infinity;-3,5) (-1;1) (2;infinity)
7-қасиет. Кез келген нақты сан х үшін [x]a болса, онда a+1x теңсіздігі орындалады.
4-мысал.
Жауабы: (-infinity;-4) (3;infinity)
8-қасиет. Кез келген нақты х саны үшін [x]a болса, онда ax теңсіздігі орындалады.
5-мысал. теңсіздігін шешіңдер
Шешуі:
Жауабы:
9-қасиет. Кез келген нақты х сан үшін {x}=a болып, n=xn+1 қос теңсіздігі орындалады; мұндағы nz
6-мысал. теңдеуін шешіңдер.
Шешуі: n

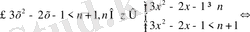
1)
D=4+12(1+n)=16+12n=4(4+3n)=0
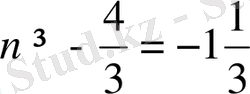
n=-1,0,1,2, болғанда

2) 3x2-2x-(2+n)0
D=4+12(2+n)=4(7+3n) =0
n=-2,0,1,2 болғанда
x3=2+27+3n6=1+7+3n3,x4=1-7+3n3

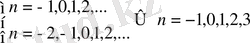болғанда

Жауабы: n=-1,0,1,2,... болғанда

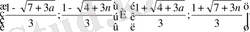
10-қасиет. Кез келген нақты сан х үшін {x}=a болса, онда ax=a+n, мұндағы nz, қос теңсіздігі орындалады.
7-мысал. теңсіздігін шешіңдер
Шешуі: 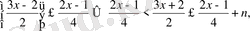мұндағы nN
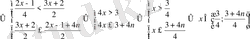; мұндағы
Жауабы: 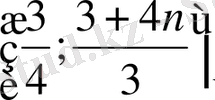мұндағы
11-қасиет. y={x} функциясы периодты функция, периоды T=1*n, мұндағы
8-мысал. Функциялардың периодтарын анықтап, графиктерін салыңыздар.
a) y={2x+1}-2 b)y= 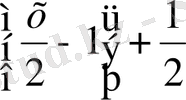c)
Шешуі: a)y={2x+1}-2 функциясының периоды T=, мұндағы болып, y={2x} функциясының графигі солға бір бірлік, төмен екі бірлікке параллель көшіріледі. (1-сурет)
б) y= 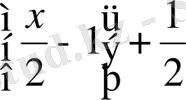функциясының периоды Т=2n , мұндағы болып, функциясының графигі оңға бір бірлік, жоғары 0,5 бірлікке оғары көшіріледі. (1-сурет)
c) 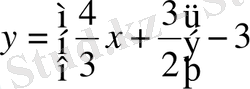функциясының периодын 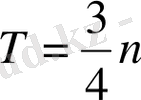, мұндағы болып,
функциясының графигі солға 1,5 бөлікке төмен 3 бірлікке параллель көшіріледі. (1-сурет)
12-қасиет. Кез келген нақты x және m сандары үшін мына теңдік орындалады:

9-мысал. теңдеуін шешіңдер, бүтін шешімдерін табыңдар.
Шешуі:
Жауабы: 5,6,7
Бұл мысалды басқаша былай шешуге болады:

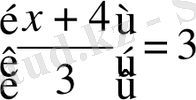
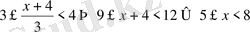
х 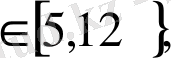бүтін шешімдері х=5;6;7 болады.
Жауабы: 5;6;7.
12-мысал. теңдеуін шешіңдер.
Шешуі: I-тәсіл.

D(f)= 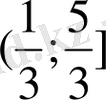болған аралықтан теңдеуден оң жағының бүтін болатын х-тің мәндерін іздестіреміз.
1) болса, онда
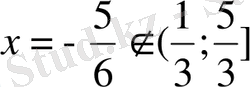
2) 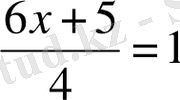болса, онда
3) болса, онда
4) 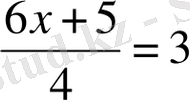болса, онда
5) 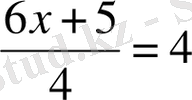болса, онда
Демек, және 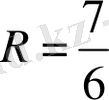сандары теңдеуін шешімі болады.
II-тәсіл. 16-шы қасиетін қолданамыз.

Жауабы:
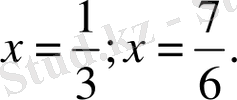
13-қасиет. Кез келген нақты сан х үшін:
a) x1 болса, [x]{x} болады;
b) x1болса, [x]{x} болады.
14-қасиет. {x-7}=a болса, мұндағы 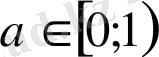болса, онда 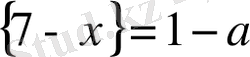теңдігі
орындалады.
15-қасиет. 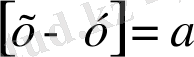, мұндағы болса, онда 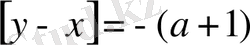теңдігі орындалады.
16-қасиет. Кез келген нақты сан х үшін [x]x[x]+1 қос теңсіздігі орындалады.
10-мысал. [3x+0,5]=x+1 теңдеуін шешіңдер.
Шешуі:
Теңдеуден оң жағы тек бүтін сандар болатындықтан, 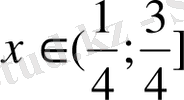аралығындағы сандарға 1-ді қосқанда бүтін сан шықпайды деген теңдеудің шешімі жоқ.
Жауабы: ∅
11-мысал. [3x+0,5]=x+1,5 теңдеуін шешіңдер.
Шешуі:
X+1,5=0 болса, онда
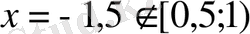
X+1,5=1 болса, онда
X+1,5=2 болса, онда
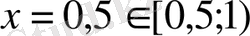
X+1,5=3 болса, онда
Тек х=0,5 қана теңдеудің шешімі бола алады.
Жауабы: x=0,5
17-қасиет. Кез келген нақты сан х үшін 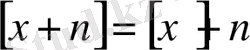теңдігі орындалады, мұндағы
18-қасиет. Тепе-теңдікті дәлелдеңдер
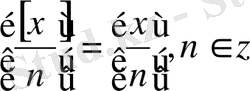
N-ге бөлінетін және х-тен артық барлық бүтін сандарды және n-ге бөлінетін [х]-тен артық емес барлық бүтін сандарды қарастырыңдар. Біріншілерінің саны , екіншілерінің саны болады. Олардың мөлшерінің теңдігінен дәлелденілетін тепе-теңдік шығады.
19-қасиет. Республикалық ғылыми-әдістемелік математика және физика журналының 2004 жылғы №3 санында О.Әжіғалиевтің Санның бүтін және оның қолданылуы атты мақаласында:
а)
теңдеуі дербес жағдайда ғана қарастырылып шешілген және натурал шешімі х=110 болған. Осы мысалды шешім көрейік [x]=x-{x} тепе-теңдігін қолданамыз.
қос теңсіздігін қолданамыз. Теңдеудің натурал шешімдері мынаған тең болады: х=110,111,112,113,114,115,116,117,1 18,119
Осы мысалды жалпылай түсірейік:
болса онда оның жалпы шешімі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.