Сызғыш пен циркульмен салу есептерінің әдістері: қиылысу, ұқсастық, инверсия, алгебралық және шешімнің бар болу принциптері


МАЗМҰНЫ
КІРІСПЕ . . . 3
І-ТАРАУ . НЕГІЗГІ ӘДІСТЕР
§1. 1. Негізгі салулар. Салу есептерін шешудің негізгі схемасы . . . 5
§ 1. 2. Қиылысу әдісі . . . . 11
§ 1. 3. Ұқсастық және инверсия әдісі . . . 17
§ 1. 4. Алгебралық әдіс . . . 24
ІІ-ТАРАУ. САЛУ ЕСЕПТЕРІНІҢ ШЕШІМІНІҢ БАР БОЛУ ПРИНЦИПЕТРІ
§ 2. 1. Есепті сызғыш пен циркульдің көмегімен салу есептерінің шешімі болатындығы туралы негізгі теоремалар . . . 31
§ 2. 2. Сызғыш пен циркульдің көмегімен шешілмейтін есептер . . . 38
Қорытынды . . . 43
Пайдаланған әдебиеттер тізімі . . . 44
КІРІСПЕ
Мектеп курсының геометрия пәнінің бір тарауы арнайы салу есептеріне бөлінген. Себебі, салу есептерінін шығару арқылы мектеп оқушылары геометрияның негізгі постулаттарын, анықтамаларын және теоремаларын меңгереді. Ол оқушылардың геометриялық фигураларды меңгеруіне үлкен септігін тигізеді.
Кейбір күрделі салу есептерін шешу өте қиын. Мұндай есептерді шешу үшін аранайы әдістер қолданылады.
Бұл диплом жұмысы жазықтықтағы фигураларды әртүрлі құралдардың көмегімен салу болып табылады. Егер арнайы құрал атауы берілмесе, онда есеп сызғыш пен циркульдің көмегімен шешіледі.
Диплом жұмысының бірінші тарауында қарапайым салулар, салу есептерін шешудің негізгі схемасы және қиылысу, ұқсастық, инверсия, алгебралық әдістер қарастырылған. Негізгі схеманың, яғни анализ, салу, дәлелдеу, зерттеу көмегімен өте күрделі есептерді шешуге болады. Салу есептерін шешудің әдістері өте көп, бірақ көбіне қиылысу, ұқсастық, инверсия, алгебралық әдістері қолданылады. Әдістерді қолданып, есептерді шығару жолдары көрсетілген.
Екінші тарауда есепті сызғыш пен циркульдің көмегімен салу есептерінің шешімі болатындығы туралы негізгі теоремалар және сызғыш пен циркульдің көмегімен шешілмейтін есептер қарастырылған. Сызғыш пен циркульдің көмегімен шешуге болмайтын есептерге: дөңгелектің квадратурасы туралы, шеңберді түзулеу туралы, бұрыштың трисенциясы туралы, кубты екі еселеу, дұрыс көпбұрыштарды салу туралы есептер жатады. Осы есептерді сызғыш пен циркульдің көмегімен салуға болмайтындығы дәлелденген.
Кейбір салу есептері тек сызғыштың немесе тек циркульдің көмегімен шешіледі. Бірінші есепті Штейнер есебі, ал екінші есепті Мор-Маскерони есебі деп атаймыз. Бұл есптерді шешу жолдарына кеңінен тоқталған.
І-ТАРАУ. НЕГІЗГІ ӘДІСТЕР
§ 1. 1. Негізгі салулар. Салу есептерін шешудің негізгі схемасы.
Кез-келген салу есебінде берілген фигуралардың көмегімен ізделінді фигураны салу болып табылады және ол белгілі бір шарттарды қанағаттандыруы қажет. Салу есебі кезінді ізделінді фигураны қандай құралдардың көмегімен салу керек екендігі ескертіледі. Егер ондай ескерту берілмесе, онда ізделінді фигураны сызғыш пен циркульдің көмегімен саламыз.
Салу есебін жүзеге асыру кезінде сызғыштың өлшем бірлігі жоқ деп есептелінеді, яғни сызғыштың көмегімен тек екі нүкте арқылы түзу жүргізуге болады. Циркульдің көмегімен тек центрі берілген нүктеде, ал радиусы берілген немесе тұрғызылған кесіндінің ұзындығына тең шеңбер салуға болады.
Кеңістікте кез-келген бір жазықтықты алайық. Оны негізгі жазықтық деп атаймыз. Қарастырып жатқан барлық фигуралар осы жазықтықта жатыр деп есептейік. Негізгі жазықтықта жатқан нүктелер, түзулер мен шеңберлер сызғыш пен циркульдің көмегімен салу есебінде маңызды рол атқарады. Сондықтан оларды негізгі фигуралар деп атаймыз. Негізгі фигуралардан басқа бізді келесі қарапайым фигуралар да қызықтырады: кесінді, сәуле, бұрыш, жарты жазықтық, көпбұрыш және шеңбер доғасы. Бірақ бұл фигуралардың әрқайсысы негізгі фигуралардың көмегімен анықталады. Мысалы AB кесіндісі A және B нүктелері мен AB түзуі арқылы анықталады.
Нүктелерді латынның үлкен әріптерімен:
A, B, C, …,
ал түзулерді латынның кіші әріптерімен:
a, b, c, …
белгілейміз. Кесінділерді:
АВ, СD, …,
ал бұрыштарды:
 ВОС
немесе
ВОС
немесе
 А
деп белгілейміз. Шеңберді
(О, r)
немесе
(O, AB)
деп белгілейміз.
А
деп белгілейміз. Шеңберді
(О, r)
немесе
(O, AB)
деп белгілейміз.
Салу есебін шығару үшін алдымен негізгі постулаттарды білу қажет.
П1 . Берілген екі нүкте арқылы түзу жүргізу.
П2 . Берілген нүктеден, берілген радиуста шеңбер жүргізу.
П3. Параллель емес екі түзудің қиылысу нүктесін салу.
П4. Шеңбер мен түзудің қиылысу нүктесін салу, егер олар қиылысса.
П5. Екі шеңбердің қиылысу нүктесін салу, егер олар қиылысса.
Енді сызғыш пен циркульдің көмегімен салу есебінің қойылуын қарастырайық.
 ақырлы негізгі фигуралар берілсін және салынбаған негізгі фигураны сипаттайтын қасиеттер берілсін. П1-П5 постулаттарының көмегімен ізделінді
Ф
фигурасын салу керек. Салу кезінде жүзеге асыратын қадамның саны ақырлы болуы керек.
ақырлы негізгі фигуралар берілсін және салынбаған негізгі фигураны сипаттайтын қасиеттер берілсін. П1-П5 постулаттарының көмегімен ізделінді
Ф
фигурасын салу керек. Салу кезінде жүзеге асыратын қадамның саны ақырлы болуы керек.
Салу есебін шешу дегеніміз, оны тізбектей орындалатын П1-П5 қарапайым салу есептерін келтіру. Алайды практикада әрбір есепті мұндай түрге келтіру тиімсіз. Көбіне есептерді П1-П5 қарапайым салу есептеріне емес, негізгі салу есептеріне НС1-НС13 келтіреді.
Оларға кеңінен тоқталып өтейік.
НС1 . Берілген сәуле бойынан, берілген кесіндіге тең кесінді салу.
НС2
. Берілген жарты жазықтықта берілген бұрышқа тең бұрыш салу.


НС3. Үш қабырғасы бойынша үшбұрыш салу.

НС4 . Екі қабырғасы мен арасындағы бұрышы бойынша үшбұрыш салу.
НС5 . Бір қабырғасы мен іргелес екі бұрышы арқылы үшбұрыш салу.
НС6. Берілген бұрыштың бисектрисасын салу.

НС7 . Берілген кесіндіге орта перпендикулярын тұрғызу.

НС8. Берілген кесіндінің ортасын салу.

НС9 . Берілген нүктеден берілген түзуге перпендикуляр түзу салу.

НС10 . Берілген нүктеден өтетін және берілген түзуге перпендикуляр түзу салу.
НС11. Сүйір бұрышы мен гипотенузасы бойынша тік бұрышты үшбұрыш салу.
НС12 . Гипотезнузасы мен катеті бойынша тік бұрышты үшбұрыш салу.
НС13 . Берілген нүктеден шеңберге жанама салу.
Күрделі салу есептерін шешу кезінде белгілі бір схема бойынша жүзеге асырылады. Ол схема келесі төрт бөліктен тұрады: анализ, салу, дәлелдеу, зерттеу.
Анализ берілген фигура мен ізделінді фигура арасындағы байланысты анықтап, оны салу есебіне қолдануды қарастырады. Анализ жүргізу үшін есепті шешілген деп есептейміз және ізделінді фигура мен берілген фигуралардың сызбасын саламыз. Онан кейін ізделінді фигурамен есептің берілгендерінің арасындағы байланысты зерттеп, ізделінді фигураны салу үшін қандай салу есептерін орындау керектігін анықтаймыз.
Салу ізделінуі фигураның сызбасын салу үшін орындалатын қарапайым (ҚС) немесе негізгі салу (НС) есептерінің тізбектеп жазып шығу. Әрбір қадамда жазылған салу есебін орындай отырып, ізделінді фигураны салу болып табылады.
Дәлелдеуде салынған фигура есептің берілген шарттарын толық қанағаттандыратынын көрсету керек. Көбіне дәлелдеу салу есебінің жолының дұрыстығынан алынады.
Зерттеу келесі сұрақтарға жауап береді.
Кез-келген жағдайда есептің шешімі бола ма?
Есептің неше шешімі болады?
Жоғарыда айтылған схема негізінде келесі есепті шешейік.
Есеп 1 . (О, r) шеңбері мен онда жатпайтын А нүктесі берілген. А нүктесінен берілген шеңберге жанама жүргізу керек.
Шешуі : Анализ . Есепті шешілген деп есептейік, яғни ізделінді фигура салынған.
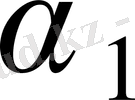
Мұнда
а
-
(О, r)
шеңберін
Р
нүктесінде жанайтын ізделінді фигура.
 тік болғандықтан, есепті шешу үшін
(О, r)
шеңберінің бойында жатқан
Р
нүктесін табу керек. Яғни
ОА
кесіндісі
тік болғандықтан, есепті шешу үшін
(О, r)
шеңберінің бойында жатқан
Р
нүктесін табу керек. Яғни
ОА
кесіндісі
 тік бұрышына қарсы жатады. Сондықтан
Р
нүктесі диаметрі
ОА
тең шеңбердің бойында жатады. Сонымен
Р
нүктесі диаметрі
ОА
тең шеңбер мен берілген шеңбердің қиылысында жатыр.
тік бұрышына қарсы жатады. Сондықтан
Р
нүктесі диаметрі
ОА
тең шеңбердің бойында жатады. Сонымен
Р
нүктесі диаметрі
ОА
тең шеңбер мен берілген шеңбердің қиылысында жатыр.
Салу .
- АОтүзуін жүргіземіз (постулат П1)
- ОАкесіндісінің ортасын саламыз (НС8)
- (М, МА) шеңберін жүргіземіз (постулат П2)
- (О, R) шеңбері мен(М, МА) шеңберінің қиылысу табамыз. (постулат П5)
- АРжәнеАQтүзулерін жүргіземіз. (постулат П1)
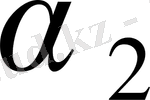
Дәлелдеу.
АР
және
АQ
түзулері ізделінді түзулер екендігі салудан түсінікті. Шынында да
 OPA
=
OPA
=
 OQA
=
90
0
, сондықтан
АР
OQA
=
90
0
, сондықтан
АР
 ОР
және
АР
ОР
және
АР
 ОQ.
Бұдан
АР
және
AQ - (О, r)
шеңберіне жүргізілген жанама екеніндігі түсінікті.
ОQ.
Бұдан
АР
және
AQ - (О, r)
шеңберіне жүргізілген жанама екеніндігі түсінікті.
Зерттеу . Есептің шешімі бар болуы үшін (М, МА) шеңбері мен (О, r) шеңберінің ортақ қиылысу нүктесі бар болуы керек. Келесі екі жағдай болуы мүмкін.
1) А нүктесі (О, r) шеңберінің ішінде жатады. Онда ОА<r немесе 2Ом<r . Бұл жағдайда (М, МА) шеңбері мен (0, 2) шеңбері қиылыспайды, сондықтан есептің шешімі жоқ.
2) А нүктесі шеңберден тысқары жатыр. Онда OA>r немесе 2OM>r . Сондықтан (М, МА) шеңбері мен (0, 2) шеңбері екі нүкте де қиылысады, сондықтан есептің екі шешімі бар.
§ 1. 2. Қиылысу әдісі.
Есепті қиылысу әдісімен шешу үшін, есепті - салу есебінің шарттарынан шығатын
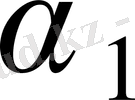 және
және
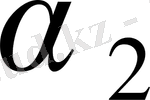 шарттарын қанағаттандыратын
Х
нүктесін салуға келтіру керек.
F
1
-
шарттарын қанағаттандыратын
Х
нүктесін салуға келтіру керек.
F
1
-
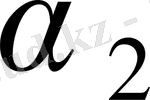 шартын қанағаттандыратын нүктелер жиыны, ал
F
2
-
шартын қанағаттандыратын нүктелер жиыны, ал
F
2
-
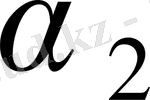 шартын қанағаттандыратын нүктелер жиыны болсын. Онда
F
1
және
шартын қанағаттандыратын нүктелер жиыны болсын. Онда
F
1
және
 F
2
қиылысында жатқан кез-келген нүктесі, ізделінді
Х
нүктесі болатындығы түсінікті.
F
2
қиылысында жатқан кез-келген нүктесі, ізделінді
Х
нүктесі болатындығы түсінікті.
Х нүктесін салу үшін, F 1 және F 2 фигуралары сызғыш пен циркульдің көмегімен салынуы қажет, яғни олар не түзулер немесе шеңберлер немесе олардың бір бөлігі болу керек.
Қиылысу әдісінде кеңінен қолданылатын кейбір жиындарды атап өтейік:
1 0 . А және В нүктесінен бірдей қашықтықта жатқан жазықтықтағы нүктелер, АВ кесіндісінің орта перпендикуляры.
2 0 . Берілген түзуден бірдей қашықтықта жатқан нүктелер жиыны, берілген түзуге параллель және берілген қашықтықта жатқан екі түзу.
3 0 . Берілген екі параллель түзуден бірдей қашықтықта жатқан нүктелердің жиыны, олардың симметрия осі болатын түзу.
4
0
.
Қиылысатын екі түзуден бірдей қашықтықта жатқан нүктелер жиыны, өзара
 болатын берілген түзулердің биссектрисалары.
болатын берілген түзулердің биссектрисалары.
5 0 . АВ кесіндісін тік бұрышқа қарсы жататындай нүктелер жиыны, диаметрі АВ тең шеңбер бойында жатқан нүктелер.
6
0
.
АВ
кесіндісі
 бұрышына қарсы жататындай нүктелер жиыны,
АВ
түзуіне симметриялы орналасқан шеттері
А
және
В
нүктелері болатын екі доға бойында жатқан нүктелер.
бұрышына қарсы жататындай нүктелер жиыны,
АВ
түзуіне симметриялы орналасқан шеттері
А
және
В
нүктелері болатын екі доға бойында жатқан нүктелер.
7
0
.
Берілген
А
және
В
нүктелерінен арақашықтықтарының айырымы тұрақты болатын нүктелер жиыны,
АВ
түзуіне
 түзі бойында жататын нүктелер.
түзі бойында жататын нүктелер.
Қиылысу әдісіне негізделген келесі есепті қарастырайық.
Есеп 2 . Берілген а және b екі параллель түзуді жанайтын және М -нүктесінен өтетін шеңберді салыңыз.
Шешуі
:
Анализ.
Есепті шешілді, яғни центрі
O
нүктесінде орналасқан
 шеңбері салынды деп есептейік. Егер
O
нүктесін тұрғызсақ, онда
(О, ОМ)
шеңбері ізделінді болады. Ал
О
нүктесі келесі екі шартты қанағаттандырады:
шеңбері салынды деп есептейік. Егер
O
нүктесін тұрғызсақ, онда
(О, ОМ)
шеңбері ізделінді болады. Ал
О
нүктесі келесі екі шартты қанағаттандырады:
 - бұл нүкте
а
және
b
параллель түзулерінен бірдей қашықтықта жатады,
- бұл нүкте
а
және
b
параллель түзулерінен бірдей қашықтықта жатады,
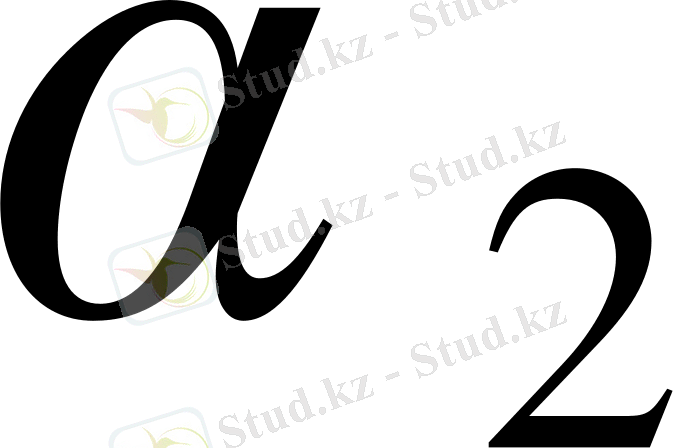 -О нүктесі
М
нүктесінен
-О нүктесі
М
нүктесінен
 қашықтықта жатады.
қашықтықта жатады.
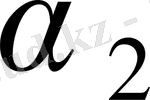
Мұнда d - параллель екі түзудің арақашықтығы.
3
0
бойынша
а
және
b
параллель екі түзуден бірей қашықтықты жатқан нүктелер жиыны, ол симметрия осі болатын
QF
1
түзуі. Ал
М
нүктесінен
d/2
қашықтықта жатқан нүктелер, ол
F
2
= (M, d/2)
шеңбері. Ал
 ізделінді нүкте.
ізделінді нүкте.
Салу.
1) а және b параллель түзуіне қандай да бір АВ перпендикулярын жүргізейік (НС 9) .
2) АВ кесіндісінің m орта перпендикулярын тұрғызайық (НС 7) .
3) АВ және m түзулерінің қиылысуы С нүктесін салайық (постулат П3) .
4) (М, АС) шеңберін жүргізейік m түзуі мен (М, АС) шеңберінің қиылысуын О деп белгілейік.
5) (О, ОМ) шеңберін салайық.

Дәлелдеу
.
(О, ОМ)
шеңберін салу бойынша
М
нүктесінен өтеді.
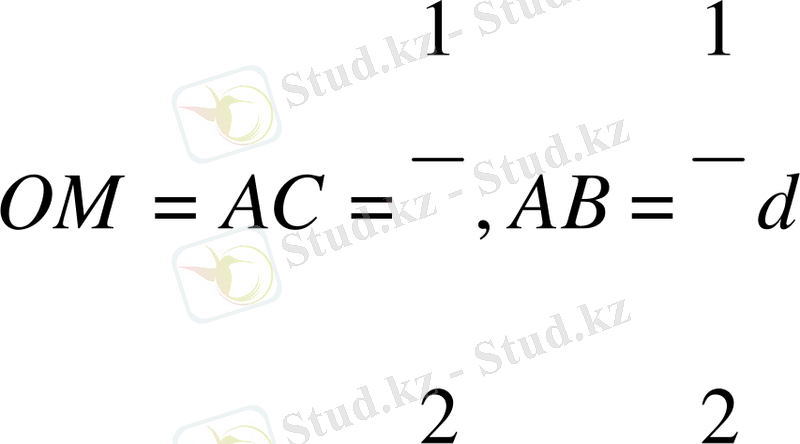 болатындықтан, ол
а
және
b
түзулерін жанайды.
болатындықтан, ол
а
және
b
түзулерін жанайды.
Зерттеу . Есептің шешімін тек m түзуі мен (М, АС) шеңбері қиылысқанда ғана болатындығы түсінікті, және оның шешімі ортақ нүктелердің санына тең. Келесі үш жағдайды қарастырайық:
1)
М
нүктесі
а
және
b
параллель түзулердің арасында жатсын. Онда
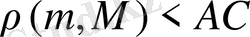 , сондықтан
(М, АС)
шеңбері мен
m
түзуінің екі ортақ нүктесі болады. Бұл жағдайда есептің екі шешімі бар болады.
, сондықтан
(М, АС)
шеңбері мен
m
түзуінің екі ортақ нүктесі болады. Бұл жағдайда есептің екі шешімі бар болады.
2)
М
нүктесі
а
және
b
түзулерінің бірінде жатсын. Бұл жағдайда
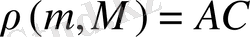 , сондықтан
(М, АС)
шеңбері m түзуін жанайды, яғни есептің жалғыз шешімі бар.
, сондықтан
(М, АС)
шеңбері m түзуін жанайды, яғни есептің жалғыз шешімі бар.

3)
М
нүктесі
а
және
b
түзулерінің арасында жатпасын. Онда
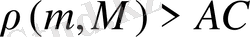 , сондықтан
(М, АС)
шеңбері мен
m
түзуінің ортақ нүктесі жоқ, яғни есептің шешімі жоқ.
, сондықтан
(М, АС)
шеңбері мен
m
түзуінің ортақ нүктесі жоқ, яғни есептің шешімі жоқ.
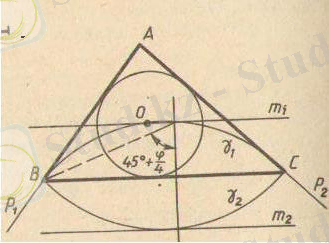
Есеп3 . Табаны, табанына қарсы жатқан бұрышы мен іштей сызылған шеңбер радиусының көмегімен үшбұрыш салыңыз.
Шешуі. Анализ . Есеп шешілген, яғни АВС үшбұрышы салынған деп есептейік.

ВС кесіндісін
а
-ға тең деп алайық, ал
b=r
және
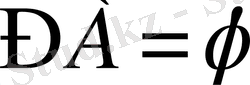 . Егер
О
нүктесін тұрғыза алсақ, онда үшінші
А
төбесін тұрғызу қиын емес. Сонымен есеп
О
нүктесін тұрғызуға келіп тіреледі.
. Егер
О
нүктесін тұрғыза алсақ, онда үшінші
А
төбесін тұрғызу қиын емес. Сонымен есеп
О
нүктесін тұрғызуға келіп тіреледі.
ВОС үшбұрышынан:
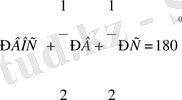 .
.
Сондықтан,
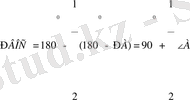 .
.
Сонымен, О нүктесі екі шартты қанағаттандырады:
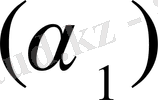 -
О
нүктесі
ВС
кесіндісінен
b
қашықтықта жатады.
-
О
нүктесі
ВС
кесіндісінен
b
қашықтықта жатады.
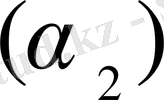 -
ВС
кесіндісі
О
нүктесінен қарағанда
-
ВС
кесіндісі
О
нүктесінен қарағанда
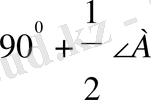 бұрышпен көрінеді.
ВС
кесіндісінен
b
қашықтықта жатқан нүктелер жиыны,
ВС
кесіндісіне параллель екі түзу.
ВС
кесіндісі
О
нүктесінен қарағанда
бұрышпен көрінеді.
ВС
кесіндісінен
b
қашықтықта жатқан нүктелер жиыны,
ВС
кесіндісіне параллель екі түзу.
ВС
кесіндісі
О
нүктесінен қарағанда
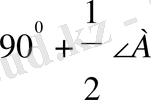 бұрышпен көрінетін нүктелер жиыны шеттері
А
және
В
нүктелері болатын екі доға.
бұрышпен көрінетін нүктелер жиыны шеттері
А
және
В
нүктелері болатын екі доға.
Салу .
- Кез- келген түзу жүргізіп, оғана-ға теңВСкесіндісін өлшеп саламыз;
- жатқанжәнетүзулерін жүргіземіз (-жиыны) ;
- бұрышы ішінде жататындай етіпжәнедоғаларын жүргіземіз (-жиыны) ;
- болатынОнүктесін тұрғызамыз;
- (О, r) -шеңберін жүргіземіз;
- ВжәнеСнүктелерінен(О, r) - жүргіземіз;
- Анүктесі осы жанамалардың қиылысу нүктесі. АВС-ізделінді үшбұрыш.

Дәлелдеу
. Салу бойынша
ВС=a
және
(О, r) -
шеңбері
АВС
үшбұрына іштей сызылған.
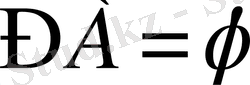 екенін дәлелдесек жеткілікті. Салу бойынша
екенін дәлелдесек жеткілікті. Салу бойынша
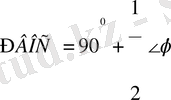 . Сондықтан ВОС үшбұрышынан:
. Сондықтан ВОС үшбұрышынан:
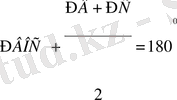 .
.
Онан
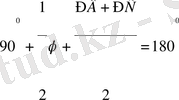 ,
,
немесе
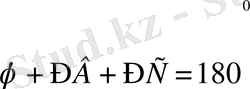 .
.
Зерттеу.
1) Алдымен есептің қай кезде шешімі бар болатындығын анықтайық.
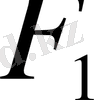 және
және
 жиындарының қиылысу нүктесі
жиындарының қиылысу нүктесі
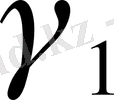 нмесе
нмесе
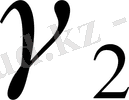 доғалары b кесіндіснен үлкен болғанда тек қана сонда бар болады. Яғни
доғалары b кесіндіснен үлкен болғанда тек қана сонда бар болады. Яғни
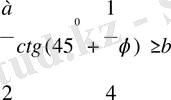
қатынасы орындалуы керек. Бұл шарт қажетті шарт болып табылады. Енді осы шарттың жеткілікті екенін дәлелдейік. Шынында да, 1) - 6) салу есептері әрдайым орындалады.
В
және
С
нүктелерінен
(О, r) -
шеңберіне жүргізілген
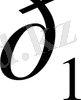 және
және
 жанамалары қиылысатынын дәлелдейік. Салу бойынша:
жанамалары қиылысатынын дәлелдейік. Салу бойынша:
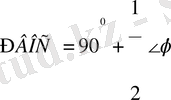 ,
,
сондықтан
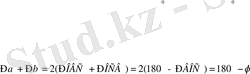 .
.
Бұдан,
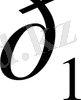 және
және
 жанамалары қиылысатындығы шығады.
жанамалары қиылысатындығы шығады.
2) Егер есептің шешімі бар болса, ол жалғыз болатындығын дәлелдеу қиын емес. Шынында да, есептің шартын қанағаттандыратын
АВС
және
А
1
В
1
С
1
екі үшбұрыш бар деп есептейік.
О
және
О
1
іштей сызылған шеңбердің центрлері болсын.
ОВС
және
О
1
В
1
С
1
үшбұрыштары тең, себебі
ВС =В
1
С
1
,
 ,
ВН=В
1
Н
1
, мұндағы
ВН
және
В
1
Н
1
-осы үшбұрыштардың биіктіктері. Мұнан
,
ВН=В
1
Н
1
, мұндағы
ВН
және
В
1
Н
1
-осы үшбұрыштардың биіктіктері. Мұнан
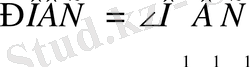 , сондықтан
, сондықтан
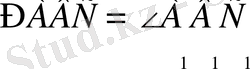 . Тура сол сияқты
. Тура сол сияқты
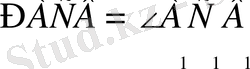 . Сондықтан
АВС
және
А
1
В
1
С
1
үшбұрыштары екі қабырғасы мен арасындағы бұрышы бойынша тең болады.
. Сондықтан
АВС
және
А
1
В
1
С
1
үшбұрыштары екі қабырғасы мен арасындағы бұрышы бойынша тең болады.
§ 1. 3. Ұқсастық және инверсия әдісі.
1. Ұқсастық әдісі.
Ұқсастық әдісінің негізгі идеясы келесі: алдымен берілген есептің тек бір шартынан басқа барлық шарттарын қанағаттандыратын ізделінді фигураға ұқсас фигураны салады.
Әдетте қосалқы фигураны тек қана ұқсас етіп емес, ол гомотетиялы болатын етіп салу тиімді. Сондықтан ұқсастық әдісімен есепті шешкенде нүктелердің гомотетия кезінде образдарын сала білу керек. Алдымен келесі есепті қарастырайық. Онан кейін гомотетияны пайдаланып, алып тасталған шаррты қанағаттандыратын фигураны анықтаймыз.
Есеп 3. Периметрі мен екі бұрышы арқылы үшбұрыш салу.
Шешуі.
Есептің берілгенін анықтап алайық:
 және
және
 бұрыштары мен
р
периметрі берілген.
бұрыштары мен
р
периметрі берілген.
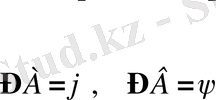 және
АВ+ВС+СА = р
болатындай үшбұрыш салу керек.
және
АВ+ВС+СА = р
болатындай үшбұрыш салу керек.
Анализ. Есеп шешілді, яғни АВС үшбұрыш салынды деп есептейік.

Бұл есеп екі шартты қанағатандырады:
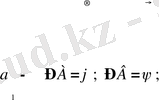 және
және
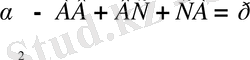 .
.
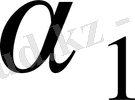 шартын қанағаттандыратын үшбұрыш салу оңай. Бұл шартты қанағаттандыратын есептің шешімі шексіз көп екенін айта кетейік.
АВ
1
С
1
- сол үшбұрыштардың бірі болсын. Енді гомотетиялы принципін пайдаланып
шартын қанағаттандыратын үшбұрыш салу оңай. Бұл шартты қанағаттандыратын есептің шешімі шексіз көп екенін айта кетейік.
АВ
1
С
1
- сол үшбұрыштардың бірі болсын. Енді гомотетиялы принципін пайдаланып
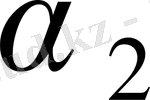 шартын қанағаттандыратын
АВ
1
С
1
үшбұрышына ұқсас
АВС
үшбұрышын салуға болады.
шартын қанағаттандыратын
АВ
1
С
1
үшбұрышына ұқсас
АВС
үшбұрышын салуға болады.
Салу.

1)
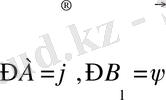 болатындай кез-келген
АВ
1
С
1
үшбұрыш саламыз.
болатындай кез-келген
АВ
1
С
1
үшбұрыш саламыз.
2)
АВ
1
сәулесінде сәйкес
 және
р
-ға тең
АD
1
және
АD
кесінділерін саламыз, мұндағы
р
1
-
АВ
1
С
1
үшбұрышының приметрі.
және
р
-ға тең
АD
1
және
АD
кесінділерін саламыз, мұндағы
р
1
-
АВ
1
С
1
үшбұрышының приметрі.
3) С 1 және В 1 нүктелерінің А центрі мен DD 1 нүктелері бойынша n гомотетиясы арқылы С және В нүктелерін тұрғызамыз.
Дәлелдеу.
АВ
1
С
1
және
АВС
үшбұрыштары гомотетиялы. Сондықтан
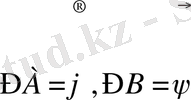 . Себебі
D = h(D
1
),
сондықтан
АD=МАD
1
,
мұндағы
m - h
гомотетиялы коэффициенті.
. Себебі
D = h(D
1
),
сондықтан
АD=МАD
1
,
мұндағы
m - h
гомотетиялы коэффициенті.
Сонымен АВ = m ·AB, BC = m·B 1 C 1 , CA = m ·C 1 A ,
Сондықтан АВ+ВС+СА = m (АВ 1 +В 1 С 1 +С 1 А) = m p 1
Сонымен АВ+ВС+СА = р
Зерттеу.
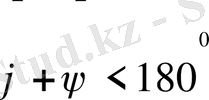 болғанда ғана есептің шешімі бар болатындығы түсінікті. Бұл шарт орындалғанда есептің жалғыз шешімі бар болады. Шынында да есептің шартын қанағаттандыратын екі үшбұрыш
АВС
және
А
1
В
1
С
1
бар болады деп есептейік. Онда
болғанда ғана есептің шешімі бар болатындығы түсінікті. Бұл шарт орындалғанда есептің жалғыз шешімі бар болады. Шынында да есептің шартын қанағаттандыратын екі үшбұрыш
АВС
және
А
1
В
1
С
1
бар болады деп есептейік. Онда

 (1. 3. 1)
(1. 3. 1)
АВ+ВС+СА = А 1 В 1 +В 1 С 1 +С 1 А 1 (1. 3. 2)
(1. 3. 1) теңдіктен
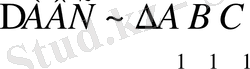 екендігі шығады. Сондықтан
AB = kA
1
B
1
, BC = kB
1
C
1
, CA = kC
1
A
1
,
мұндағы
k
- ұқсастық коэффициенті. Бұдан
АВ+ВС+СА = k (А
1
В
1
+В
1
С
1
+С
1
А
1
) .
Бұл теңдікті (1. 3. 2) теңдікпен салыстырсақ, онда
k = 1
, сондықтан
екендігі шығады. Сондықтан
AB = kA
1
B
1
, BC = kB
1
C
1
, CA = kC
1
A
1
,
мұндағы
k
- ұқсастық коэффициенті. Бұдан
АВ+ВС+СА = k (А
1
В
1
+В
1
С
1
+С
1
А
1
) .
Бұл теңдікті (1. 3. 2) теңдікпен салыстырсақ, онда
k = 1
, сондықтан
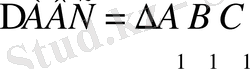
2. Инверсия әдісі.
Жазықтықта (O, r) шеңбер берілсін. О нүктесінен басқа нүктелердің барлық жиынын Е 0 деп белгілеп алайық. Е 0 жиынның әрбір М нүктесіне ОМ сәулесінде жататын М ’ нүктесін сәйкес қояйық және ОМ·ОМ ’ = r 2 .

208 - сурет.
Сонда Е 0 жиынын (O, r) шеңберіне қатысты түрлендірілген жиынын аламыз. Ол жиынды инверсиялы жиын деп атаймыз. (O, r) - шеңберін инверсия шеңбері, О - нүктесін инверсия центрі, ал r 2 - инверсия дәрежесі деп аталады.
Есеп 4. (O, r) инверсия шеңбері берілсін. Шеңбердің бойында жатпайтын М нүктесінің М ’ образын табыңыз.
Шешуі.
Алдымен
М
нүктесі инверсия шеңберінен тыс жатқан нүкте болсын деп есептейік.
ОМ
сәулесі және диаметрі
ОМ
-ге тең
 шеңберін жүргізейік.
шеңберін жүргізейік.

Р
және
Q
нүктелері
(O, r)
шеңбері мен
 шеңберінің қиылысу нүктесі болсын. Онда
М
’
-
ОМ
және
РQ
түзулерінің қиылысу нүктесі болады. Шынында
МР
және
МQ
-
(O, r)
- шеңберінің жанамалары болады, сондықтан
ОРМ
және
РМ
’
М
бұрыштары тік. Бұдан
шеңберінің қиылысу нүктесі болсын. Онда
М
’
-
ОМ
және
РQ
түзулерінің қиылысу нүктесі болады. Шынында
МР
және
МQ
-
(O, r)
- шеңберінің жанамалары болады, сондықтан
ОРМ
және
РМ
’
М
бұрыштары тік. Бұдан
 екендігі шығады. Сонымен,
екендігі шығады. Сонымен,
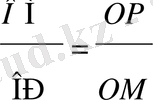 немесе
немесе
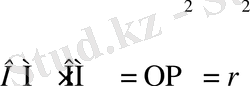 .
.
Егер М - инверсия шеңберіне қатысты ішкі нүкте болса, онда М нүктесін тұрғызу кері қарай жүзеге асырылады.
Инверсия қасиеттерін зерттеу үшін, оның аналитикалық өрнектелуін қарастырайық. Оij - жүйесін О инверсия центрі координаталар басы болатындай етіп алайық.
М(х, у) - Е
0
жиынының кез-келген нүктесі болсын, ал
М
’
(х
’
, y
’
)
- оның образы. Инверсияның анықтамасы бойынша
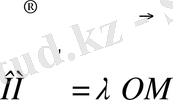 және
және
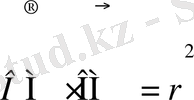 екендігі шығады, мұндағы
λ > 0
.
екендігі шығады, мұндағы
λ > 0
.
Координаталары арқылы бұл теңдіктер келесі түрде жазылады:
x ’ = λx, y ’ = λy, мұндағы х>0 (1. 3. 3)
хх ’ + уу ’ = r 2 (1. 3. 4)
(1. 3. 3) теңдіктегі
х
’
және
у
’
мәндерін (1. 3. 4) қойсақ, онда
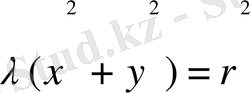 .
М
нүктесі
О
нүктесімен беттеспегендіктен,
.
М
нүктесі
О
нүктесімен беттеспегендіктен,
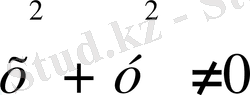 , сондықтан
, сондықтан
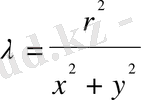 . Табылған λ мәнін (1) - қойсақ:
. Табылған λ мәнін (1) - қойсақ:
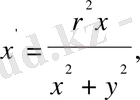
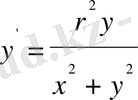 (1. 3. 5)
(1. 3. 5)
Кері түрлендіру бірмәнді екенін ескерсек:
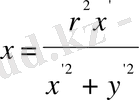 ,
,
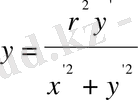 (1. 3. 6)
(1. 3. 6)
Теорема 1. Инверсия центрінен өтетін түзу өзіде-өзіне, ал инверсия центрінен өтпейтін түзу инверсия центрінен өтетін шеңберге түрленеді.
Дәлелдеу. Теорема бірінші бөлігі инверсия анықтамасынан шығады.
Теореманың екінші бөлігін дәлелдейік. Ах+Ву+1=0 инверсия центрінен өтпейтін кез-келген түзу болсын, онда оның образы
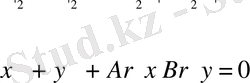 . (1. 3. 7)
. (1. 3. 7)
Ал, бұл инверсия центрінен өтетін шеңбер.
Салдар. Егер d түзуі О инверсия центрінен өтпейтін түзі (С, r) шеңберіне түрленсе, онда ОС және d түзулері перпендикуляр.
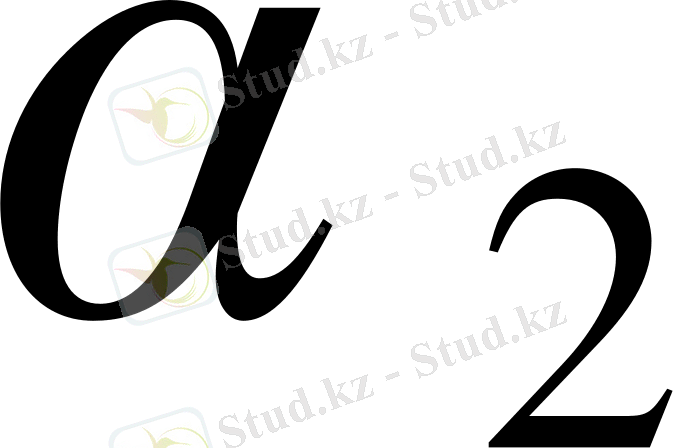

Теорема 2. О инверсия центрінен өтетін шеңбер, инверсия центрінен өтпейтін түзуге түрленеді. О нүктесінен өтпейтін О нүктесінен шеңберге түрленеді және О нүктесі осы шеңберлердің центрінен өтетін сызық бойында жатады.
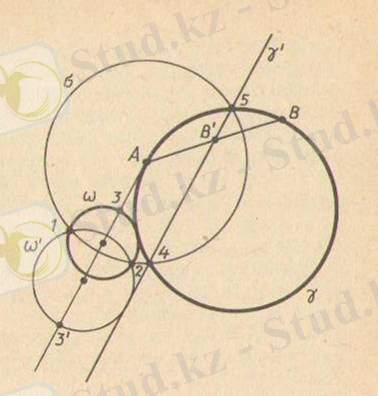
Есеп 5.
 -шеңбері мен осы шеңбердің бойында жататын
А
және
В
нүктелері берілсін.
А
және
В
нүктелерінен өтетін және берілген шеңберді жанайтын шеңбер салу керек.
-шеңбері мен осы шеңбердің бойында жататын
А
және
В
нүктелері берілсін.
А
және
В
нүктелерінен өтетін және берілген шеңберді жанайтын шеңбер салу керек.
Шешуі.
Анализ
. Берілген есеп шешілді және
 шеңбері тұрғызылды деп есептейік.
шеңбері тұрғызылды деп есептейік.

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz