ХИМИЯЛЫҚ ТЕРМОДИНАМИКАНЫҢ НЕГІЗІ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 81 бет
Таңдаулыға:

ХИМИЯЛЫҚ ТЕРМОДИНАМИКАНЫҢ НЕГІЗІ
§ 1. ТЕРМОДИНАМИКАНЫҢ БІРІНШІ ЗАҢЫ
Термодинамикалық түсініктер мен анықтамалар. Термодинамика денелер энергиясының бір-біріне жылу мен жұмыс түрінде өзгеруін, айналуын зерттейді. Қоршаған ортадағы энергияның осылай алмасуы термодинамикада сандық сипаттама ретінде қарастырылады. Жылу, электрон, атом, молекула сияқты бөлшектердің ретсіз қозғалысын, яғни олардың кинетикалық энергиясының жылу түріндегі энергиямен алмасуын, ал жұмыс -- сол бөлшектердің реттелген козғалысын кинетикалық энергия түрінде сипаттайды.
Термодинамика негізінен термодинамиканың бірінші және екінші заңдары деп аталатын екі заңдылыққа сүйенеді. Олардың, екеуі де өмірдегі, өндірістегі тәжірибелерді жинақтап, қорытып, тұжырымдаудан пайда болған. Термодинамика мынадай тараулардан тұрады: энергияның бір түрден екіншіге түрленуіндегі жалпы заңдылықты зерттейтін жалпы немесе физикалық термодинамика, жылу машиналарындағы жылу мен механикалық жұмыстың өзара айналуын, яғни жылудың жұмысқа, жұмыстың жылуға ауысуын қарастыратын техникалық термодинамика, химиялық реакция, еру, кристалдану, адсорбция сияқты процестердегі энергия түрлерінің өзара алмасуын, айналуын анықтап, есептейтін химия-лық термодинамика. Сол сияқты, химиялық термодинамика тек химиялық және басқа да энергиялардағы ара қатынасты зерттеп қана қоймай, белгілі жағдайдағы химиялық процестердің мүмкіндігі мен өздігінен жүру шегін айқындайды. Ендеше, химиялық термодинамика химиялық өндіріс пен технологиялық процестер негізі болып саналатын физикалық-химиялық құбылыстарды нақты түсініп, сауатты есептеп, ұтымды басқаруға көмектеседі.
Термодинамикалық әдістегі есептеулерді қолдану өндірістің барлық салаларына өз ықпалын тигізіп, оларды жаңа сатыға көтерді. Ал, қазіргі кезде термодинамикалық әдіс металлургиялық процестерде, пластикалық масса (пластмасса), тыңайтқыш, химиялық талшық өндірісінде, отынды химиялық әдіспен өңдеуде кеңінен қолданылуда. Әсіресе, соңғы жылдары биологиялық термодинамиканың шапшаң дамуына байланысты, өсімдік пен жануар организмдеріндегі биохимиялық процестерге де термодинамикалық есептеу әдістері қолданылуда.
Термодинамиканың, алғашқы бағыты табиғатта кездесетін құбылыстарды жай ғана баяндаудан басталып, жылу мен энергия түрлері арасындағы қатынасты сипаттап қаиа қоймай, оны есептеуді игерді. Термодинамика математика, физика, химия сияқты түбегейлі ғылым салаларымен тығыз байланыста бірін-бірі толықтыра келіп, ішкі энергияның айналуын анықтап, бағытын, мүмкіндігін көрсетеді. Ал, соңғы жетістіктерге сүйеніп, термодинамика :көптеген процестерді есептеп, анықтап, ондағы энергияның қалайша түрленетінін нұсқап қоймастан, жалпы процестің жүру, жүрмеуін алдын ала болжайды.
Термодинамика сондай-ақ, классикалық және статистикалық болып та бөлінеді. Қлассикалық (дәстүрлі) термодинамика жекеленген атом, молекула сияқты бөлшектерді емес, бу машиналарының, іштен жанатын двигательдердің жұмыс істеу ерекшеліктерін, сүйықты қайнатып айдау, кристалдану, электролиз сияқты микроскопиялык жүйелерді зерттейді. Ал статистикалық термодинамика кейін пайда болса да, термодинамика ілімін едәуір дамытып, жаңа сатыға көтерді. Статистикалық термодинамика жекеленген атом, молекула секілді бөлшектерді қарастырады, олардың біріккен сипаты мен қасиеттерін айқындайды. Термодинамиканың бұл екі саласын білу болашақ химик, биолог, технологтардың кәсіби ма-мандықтарының деңгейін жаңа сапаға көтереді.
Термодинамиканы кейде энергетика деп те атайды. Ол зерттеуші қолындағы аеа қуатты қару, таптырмас әдіс болса да, бәрін шеше бермейді. Оның көмегімен белгілі процесс кезінде алынатын барынша тиімді, мейлінше пайдалы жұмысты болжап айтуға, тепе-теңдік күйді анықтауға, жоғары шығымды, жүріп жатқан реакция үшін тиімді температураны, қысымды, еріткіш ортаны, т. с. с. білу-ге болады. Сондай-ақ, термодинамика берілген реакцияның жүру, жүрмеуін, бағытын анықтайды. Бірақ осы реакция жүру үшін қанша уақыт қажет, ол қандай жолмен жүреді деген сауалдарға жауап бере алмайды.
Термодинамикалық система (көбіне тек система) деп қоршаған ортадан бөлініп алынған денені немесе денелер тобын айтады. Ал системадан тыс қалғандарды қоршаған орта дейді. Системаның фазааралық не ойша бөлінген шекарасы болады. Осылайша бөлініп алынған системадағы молекулалар саны көп болу қажет. Егер системадағы молекула саны аз болса, оны термодинамика қарастырмайды.
Системаның өзін қоршаған ортамен қатынасы энергияның механикалық, жылулық немесе басқа да түрлерімен және затпен алмасқан мезеттерде жүзеге асады. Егер осы айтылғандардың бірде-бірі жүзеге аспаса, онда мұндай системаны оқшауланған система дейді. Ал система мен оны қоршаған орта арасындағы қатынас энергия түрлері арқылы жүзеге асып, онда зат қатынаспаса (алмаспаса), системаны жабық, кейде түйықталған деп атайды. Зат салынған жабық ыдыс, газы бар баллон және баскалар жабық системаларға мысал болады. Системадан шығатын зат та, энергия түрлері де оны қоршаған ортаға жетіп алмасса және бұл құбылыс кері бағытта да жүретін болса, оларды ашық система дейді. Өсімдіктер мен жануарлар дүниесі ашық системаға айқын мысал. Мұндағы система -- өсімдік, жануар (тірі организм), оны қоршаған орта -- атмосфера (ауа), қатынастырушы зат -- қоректік заттар, энергия -- химиялық реакциялар кезінде бөлінетін жылу, заттардың тотығуы.
Системаның күйі көлем, қысым, температура, масса, химиялық құрам сияқты параметрлермен және химиялық қасиеттердің жи-

ынтығымен сипатталады. Мұнымен қатар система күйін көрсететін бірнеше теңдеулер де бар. Система күйін анықтау үшін көрсетілген өлшемдердің бәрін білу шарт емес, өйткені олар теңдеу құрамына енгендіктен, бірін-бірі толықтырады және өзара байланысты болады. Система күйін анықтау үшін таңдалып алынған бірнеше тәуелсіз ауыспалы шамадағы қасиет көрсеткішін күй параметрлері (өлшемі) дейді. Оларды белгілі бір жағдайда өтетін процеске орай таңдайды. Мәселен, газ күйін сипаттау үшін оның қысымы, көлемі және температурасы сияқты үш өлшемнің екеуін алсақ жеткілікті, себебі қалғаны осыларға әр уақытта да тәуелді болады.
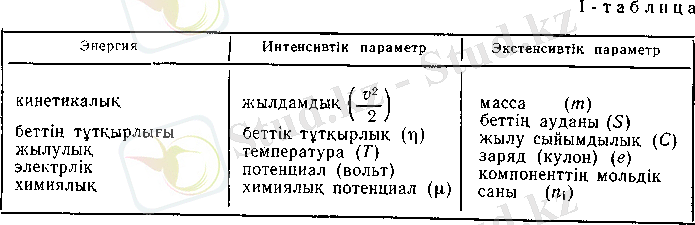
Күй параметрлерін экстенсивтік және интенсивтік деп бөледі. Экстенсивтік параметрлер мысалы, көлем, масса системадағы заттың санына пропорционалды. Ал интенсивтік параметрлер мәселен, температура, қысым, тұтқырлық, концентрация заттың санына (мөлшеріне) тәуелді емес. 1-таблицада энергияның интенсивтік параметрлермен байланысы көрсетілген. Бұған зер салып қарасақ, энергияның параметрлермен табиғи байланысын көріп, көптеген коэффициенттерді пайдаланып, энергияның бір түрі басқа түрге қалай ауысатынын және олардың өлшем бірліктерінің де қалай өзгеретінін, ішкі байланысын байқаймыз. Интенсивтік не экстенсивтік параметрлерді интенсивтік фактор және экстенсивтік (сы-йымдылық) фактор деп те атайды. Энергияның әр түрлі мәнінде тұрған интенсивтік немесе экстенсивтік параметрлердің орнын ауыстыруға болатыны сияқты, жекеленген параметрлерді (интен-сивтік не экстенсивтік (сыйымдылық) фактор болсын) осындағы басқа параметрлермен ауыстыруға болмайды.
Система күйіндегі параметрлердің кез келген өзгерісі процесс деп аталады. Оқулықта жиі кездесетін процестердің кейбір түрлері мыналар:
1. Изотермалық процесс (Т = const)
2. Изобаралық процесс (ρ = const)
3. Изохоралык процесс (V = const)
4. Адиабаталық процесс (Q = 0)
5. Изобара-изотермалық процесс (р = const; Т = const)
6. Изохора-изотермалық процесс (V = const; Т = const).
Система күйінің біраз параметрлері процесс нәтижесінде өзгеріп, соңында өздерінің бастапқы мәніне қайта оралса, онда мұндай процестерді тұйық процестер деп атайды.
Егер системада энергия немесе зат алмасу болмаса және оның касиеті уақыт өткен сайын өзгермесе, онда мұндай системаның, күйін күй теңдігі дейді. Әйтсе де, ортадан тепкіш күштің, электрлік және басқа сыртқы әсер ету күштерінің өрісіндегі системаның тепе-теңдік кезіндегі интенсивті қасиеттері бір нүктеден екінші нүктеге ауыса алады, яғни өзгереді, бұл өзгерістерді ескермеуге де болады. Системаның тепе-теңдік күйін уақыт өткен сайын қасиеті өзгеріссіз қалатын тұрақты күйден ажырата білу қажет.
Бір процестегі система тепе-теңдіктегі күйдің біразынан үздіксіз өтсе, оларды тепе-теңдіктегі немесе квази теңдіктегі деп айтады. Бұл жағдайда қарастырып отырған система ішіндегі тепе-теңдікті және оның жекелеген бөліктері арасындағы, сол сияқты системаның өзін қоршаған ортамен шектелген шекарасындағы тепе-теңдікті де қосады. Мүндағы, жекеленген бөліктер мен системаны қоршаған орта арасындағы әрекет процесс сипатына ешбір нұқсан келтірмейді. Егер қоршаған ортадағы процесс те тепе-теқдікте болса, онда қарастырылатын системаның кез келген аралықтан немесе соңғы күйден бастапқы қалыпқа (күйге) оралу мүмкіндігі болады және осы кездерде сыртқы ортада ешқандай өзгеріс қалмайды. Мұндай процестерді қайтымды дейді. Тепе-теңдіктегі және қайтымды процестер ете баяу жүреді. Тіршіліктегі іске асатын әр процестің соңғы жылдамдығы болады және ондай процестер қайтымсыз келеді. Тепе-теңдіктегі қайтымды процестерді сипаттайтын қатынастарды термодинамиканың негізгі заңдылықтарына сүйеніп есептеуге болады.
Енді осы процестерді шағын тәжірибе арқылы талдап көрейік: ол үшін тұрақты температурадағы газы бар цилиндрді ешбір кедергісіз еркін қозғалатын поршеньмен жабайық. Поршеньге жоғарыдан күш әсер етпесе, ол белгілі бір биіктікте қозғалыссыз тұрады. Бұл процесті түсіндіру үшін 2-суретте көрсетілгендей үш түрлі гирь тастарын алайық. Олардың бірінші түрі бір килограмдық үш гирь тасы, екіншісі -- жарты килограмдық алты гирь тасы, ал үшіншісі -- ол да үш килограмдық, бірақ ол әрбір түйіршігі бір грамдық құм қиыршығынан тұрады. Енді цилиндр поршенінің үстіне бір килограмдық бір гирь тасын қойсақ, поршень цилиндрдегі ауаны қысып, көлемін кішірейтіп, төмендейді, екінші және үшінщі гирь тасын қойғанда да осы процесс қайталанады. Процесс соңында поршень үш саты арқылы өзінің ең төменгі деңгейіне жетіп тоқтайды. Осы кезде цилиндрдегі газ көлемі VІ-ден (бастапқы көлем) V2-ге өзгереді. Мұны кері жүргізуге де болады. Ол үшін кезекпен әрбір килограмдық гирь тасын бір-бірден алса, поршень үш сатылы процесс арқылы жоғары көтеріліп, өзінің, қалпына келеді, мұнда газ қысымы азайып, көлемі көбейеді. Осы бір-біріне Қарама-қарсы екі процестің өзгеруі 2, а-суретте көрсетілген. Ондағы төменгі сынық сызық гирь тастарын поршеньге салғандағы, ал жоғарғысы оларды біртіндеп алғандағы процестерді аңғартады.

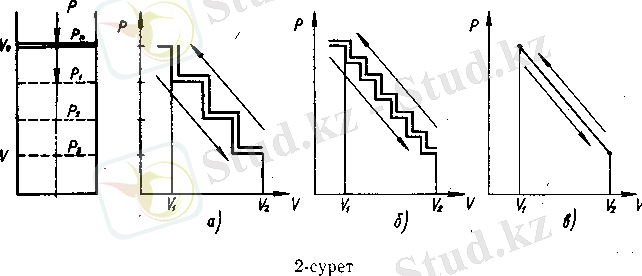
Әрбір саты немесе секіру бір килограмдық гирь тасын қосқанға (төменгі), не алғанға (жоғарғы) тең. Демек, төменгі сынық сызықтың әрбір секіруі қысымның (жүктің) көбеюін және соған сәйкес цилиндр ішіндегі газ көлемінің азаюын көрсетсе, жоғарғы сынық сызықтың әрбір секіруі поршеньге түсірілген қысымның (жүктің) кемуі мен соған орай газ көлемінің көбеюін сипаттайды. Осы кездердегі цилиндр поршенінің жоғары-төмен қозғалуынан пайда болатын жұмыс -- төменгі сызықтың астындағы ауданға, ал газ кө-лемінің ұлғайғандағы жұмыс -- үстіңгі сызықтың астындағы ауданға тең. Бұдан поршеньнің газды қысқандағы жұмысынан гөрі, газдың көлемін көбейту кезіндегі жұмыстың артық екені көрінеді. Енді осы процесті қайталайық (2, б-сурет), тек мұнда жарты килограмдық алты гирь тасы бар. Мұнда да поршеньге түскен күш (кысым) көбейген сайын, газ көлемі азайып, төменгі қисықпен өрнектелсе, енді оған керісінше әрбір гирь тасын алып, поршень қысымын секірмелі азайтқанда, оған сәйкес цилиндр ішіндегі газ көлемі секірмелі түрде артып отырады және ол жоғарғы сызықпен сипатталады. Мұнда екінші процестегі газдың жұмысы біріншісінікінен артық.
Бұл процесті басқаша да қайталауға болады. Егер поршень арқылы цилиндр ішіндегі газға түсетін қысымды шексіз кіші шамаға көбейтсе, мұндағы процесс бірқалыпты өзгереді және оны дәл осы тәртіппен, қысымды шексіз кіші шамаға кеміткенде де бірқалыпты жүреді. Поршеньге әрқайсысы бір грамдық құм түйіршігін бір-бірлеп салса, газға түсетін қысым бірқалыпты көбейеді де, газдың көлемі баяу азаяды. Мұндайда, бірінші тәжірибедегі үш саты екіншіде алтыға бөлінсе, үшіншіде үш мың сатыға бөлінеді екен (2, в-сурет). Демек, әсер етуші қысымды шексіз кіші бөлшекке жіктеу әлгі сынық сызықты да соншаға бөлумен бірдей. Олай болса, газды қысуды көрсететін төменгі қисық газ қысымының азаюы мен көлемінің көбеюін бейнелейтін жоғарғы сызыққа жақындайды да тепе-теңдікке ұмтылады. Мұндайда сызық астындағы көлем де теңеледі. Осы шартқа орай газ көлемі азайғандағы жұмыс ең аз, ал газ көлемі көбейгендегі жұмыс ең көп болады.
Ішкі энергия. Ішкі энергия (U) системаның жалпы энергия қорын сипаттайды. Оның құрамына системаны кұрайтын электрондардың, ядролардың, атомдардың, молекулалардың, бөлшектердің, өзара әрекеті мен қозғалыстарындағы энергияның барлық түрлері енеді. Әйтсе де ішкі энергияра сыртқы күш өрісіндегі потенциалдық энергия мен системадағы кинетикалық энергия енбейді. Оның абсолюттік мәнін ең, қарапайым система үшін де анықтау мүмкін емес және термодинамика мақсаты үшін ол керек емес. Система бір күйден екіншіге ауысқан кездегі оның, ішкі энергия өзгерісінің мәнін табу маңызды ΔU= U2 - U1. Қарастырылып отырған процестегі системанық ішкі энергиясы көбейсе (артса), онда ΔU оң, азайса теріс болады.
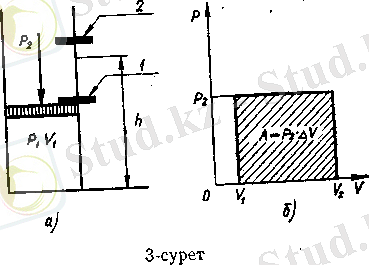
Система өзін қоршаған ортамен әрекеттескенде пайда болатын құбылысты жұмыс дейді. Осындай жұмыс нәтижесінде системаның тепе-теңдігін бұзған сыртқы күш жойылады. Сонымен жұмыс дегеніміз энергияны берудің макроскопиялық түрі екен. Олай болса, жұмыс жүргізілуі үшін сыртқы күштің болуы шарт. Енді осы ойды түсіндіру мақсатымен, газ көлемінің, үлғаюы кезіндегі жұмысты қарастырайық (З-сурет).рІ бастапқы қысым -- және V2 көлемі басым. Цилиндрдің 1 және 2 нүктесінде поршеньді ұстап тұратын шектеуіштер орнатылған делік (3, а-сурет). Поршеньге сырттан қысым түсірілсін, ол поршень астындағы, яғни цилиндр ішіндегі әуелгі қысымнан р1 аз болсын: р2р1. Егер 1-шектеуішті босатсақ, онда газдың көлемі ұлғайып, кысымның көлем өзгерісіне көбейтіндісіне тең шамадағы жұмыс атқарылады:
А = р2 · (V2-V1) =р2 ΔV (3, б-сурет). Поршеньнің сыртқы қысымы р2 азайған сайын, газ көлемінің, ұлғаюы кезінде атқарылатын жұмыс шамасы да азаяды және р2 = 0 болса, А = 0. Ал, сыртқы қысым ішкі қысымнан шексіз аз мөлшердегі қысымға ғана артық болса, онда ең көп жұмыс атқарылады, оны максималды жұмыс дейді.
Жылу дегеніміз бір-біріне түйіскен денелердегі молекулалардың өзара соқтығысу (қақтығысу) арқылы, яғни система ішінде жылу алмасу жолымен энергияны беру, жеткізу түрі. Ал жылу алмасу -- макроскопиялық не ретсіз қозғалыстағы бөлшектердің энергияны беру түрі. Жылудың бағытын және өзара берілуін, қозғалысьн температура көрсетеді.
Жұмыс (А) пен жылу (Q) ішкі энергия (U) сияқты системалардың қасиетін көрсетпейді, олар тек энер-гияны бір системадан екіншіге жеткізеді. Жылуды беру немесе жұмысты атқару үшін система өзін қоршаған ортамен не басқа системалармен әрекеттесуі қажет. Көбіне, система өзін қоршаған ортамен не басқа систе-малармен әрекеттесуі қажет. Әдетте, система өзін

қоршаған ортадан не басқа системадан жылу алса, жылуды және осы кездегі система атқарған жұмысты оң, ал кері жағдайда теріс дейді.
Энтальпия. Қөптеген процестерді термодинамикалық тұрғыдан қарастырғанда ішкі энергиямен қатар

функциясы да жиі кездеседі. Мұндағы р -- система қысымы; V -- система көлемі. Осы теңдеудің оң жағындағы көбейтіндіні (рV) системадағы потенциалды энергиямен теңестіруге болады. Энтальпияны системадағы кеңейтілген энергия немесе жылу ұстағыштық деп те айтады. Энталышя да ішкі энергия сияқты система күйінің функциясы және оның процестер кезіндегі өзгеруі. Ол процестердің қалай, қандай жолмен өткеніне тәуелді емес, тек системаның бастапқы және соңғы күйіне байланысты. Энталышяның абсолюттік мәнін анықтау мүмкін емес. Өйткені оны өрнектейтін термодинамикалық теңдеу белгісіз және табуға мүмкіндік жоқ. Сондықтан да көптеген процестерде энтальпия мәнінің өзгеруі ғана ескеріледі:
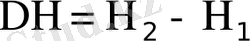(10)
Энтальпия терминін 1909 жылы Оннес енгізген, ол гректің эн -- ішкі және тальпэ -- жылу деген сөздерінен алынған.
Термодинамиканың бірінші заңы. Термодинамиканың бірінші заңы (кейде оны термодинамиканың бірінші бастамасы дейді) негізінен энергияның сақталу және оның жылу процестеріне түрлену (айналу) зады болып есептеледі. Демек, ол жылу мен жұмыстың өзгеруіне байланысты. Ал, энергияның сақталу заңы ғылымға көптен белгілі. Өйткені табиғаттың осы заңдылығы макросистемалардағы процестерге де, молекула саны аз қатынасатын өте кішкене системаларға да қолданылады. Ол, әуелі механикадағы жылу мен жұмыс арасындағы қатынастарды зерттеп, анықтау кезінде қалыптасып, бертін магниттік және электрлік энергиялардың байланысын түсіндіру үшін электрлік теорияда колданылды. Осы айтылған екі жағдайда да жылу алмасу қарастырылмай, тек энергияның бір формадан екінші формаға ауысуы ғана алынған.
Макроскопиялык. системалардағы энергияның өзгеруі тәжірибе көрсетіп отырғандай жылу алмасу формасында байқалады және сан түрлі жүмыс түрінде кездеседі. Көптеген әдістер арқылы бір күйден екінші күйге ауысқан жылу мен жұмыстың алгебралық қосындысы өздерінің тұрақты мәнін сактайды, ал процестерде ол нөлге тең. Жүргізілетін тәжірибелер нәтижесінен, термодинамиканың бірінші заңы сипаттауды, дәлелдеуді керек етпейтін жорамал (постулат) екенін көреміз. Осыған сүйеніп системадағы ішкі энергияның қосындысы тек система күйіне ғана тәуелді функция екенін аламыз. Мысалы, жабық системаға белгілі мелшердегі жылу (Q) жібеірілді делік. Бұл жылу жалпы жағдайдағы системаның ішкі энергиясын (U) көбейтуге және сол системаның істеген жұмысына (А) кетеді. Демек, термодинамиканың бірінші заңын былай тұжырымдауға болады: кез келген процестердегі системаныц ішкі энер-гия өсімшесі, осы системага берілген жылу мөлшерінен система атқйрған жұмысты азайтқанға тең:

Бұдан ішкі энергияның өзгеруі процестерді қалай, қандай жолмен жүргізгенге байланысты емес, системаның бастапқы және соңғы күйіне тәуелді екенін көреміз. Бұл, ішкі энергияның система күйінің функциясы екенін дәлелдейді. Егер функцияның мәні күй параметріне ғана байланысты болып, процестің бұрынғы күйімен анықталмаса, онда ол функцияны күй параметріне функциялы деп те айтады. Жылу мен жұмыс мұндай қасиет көрсетпейді, олар система күйінің функциясы емес және процестердің қалай, қандай жолмен жүргізілгеніне тәуелді. Осы айтылғандарды нақтылай түсу үшін, термодинамиканың бірінші заңының дифференциалдық түрін математикалық өрнекпен көрсетейік:

(10) және (11) теңдеулер -- термодинамиканың бірінші заңының аналитикалық мәні. Оларды өткен ғасырдың ортасында, бір-бірінен тәуелсіз әуелі Р. Майер, сосын Д. Джоуль ашқан. Алғашында бұл теңдеулер тек механикалық жұмыстарды сипаттауға ғана қолданылған. Бертін келе Г. Гельмгольц оларды жалпы түрге ауыстырды. Бұл теңдеулердегі А кез келген жұмыс түрін көрсетеді. Ал, жалпы жұмыс мөлшері системаға әсер еткен күштердің қосындысының жүргізілген жұмыс жолына көбейтіндісіне тең. Газ өз көлемінің улғаюы кезіндегі жұмыстар жиірек қарастырылады.

мұндағы А' -- система көлемі өзгергендегі жұмыс және оны пайдалы жұмыс деп атайды.
Химиялық термодинамикада химиялық өзгеріс кезінде пайдалы жұмыс алудың мәні зор. Мысалы, оқшауланған системаларда жылудың да, жұмыстың да өзгерісі болмайтындықтан, термодинамиканың бірінші заңы былай өрнектеледі: :
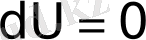
(14)
яғни оқшауланған системалардағы ішкі знергия тұрақты шама.
Ашық системалар үшін, ішкі энергияның экстенсивтік шама және оның система массасына байланысты екенін ескерген жөн. Олай болса, термодинамиканың бірінші заңы ашық системалар үшін:
U=QA+EM және dU=δQδA+dEM (15)
мұндағы Ем системадағы масса өзгерісіне байланысты энергия.
Термохимия. Системаның ішкі энергиясы химиялық реакция кезінде едәуір өзгерістерге кезігеді. Бұған басты себеп, реакция нәтижесінде алынған қосылыстар мен реакцияға түсетін заттардың ішкі энергияларының айырмашылығы бар. Мұны қарастырудың маңызы термодинамикалық есептеулер үшін зор және ол молекулалардағы жекелеген химиялық байланыстардың, күшін бағалап, энергиясын зерттеу, олардың сандық мәнін табу үшін керек. Химиялық реакциялар кезіндегі ішкі энергияның өзгеруі, жалпьг барлық процестердегі секілді, жылуды сіңіру немесе бөліп шығару және мұның салдарынан жұмыстың атқарылуы сияқты құбылыстармен тығыз байланыста өтеді. Әдетте, мұндағы жұмыс өте аз болады. Ал, химиялық реакциялар кезінде пайда болатын жылу термодинамиканың термохимия (жылу химиясы) деп аталатын тарауында қарастырылады. Енді химиялық реакциялардың жылу эффектісі (әсері) ұғымын енгізелік. Химиялық реакциялардың жылу эффектісі деп химиялық реакция нәтижесінде бөлінетін немесе сіңірілетін жылуды айтады. Осы тұжырым дәл болу үшін мынадай үш шарт орындалуы керек:
1. Көлем немесе кысым тұрақты.
2. Көлемнің ұлғаю кезінде пайда болатын жұмыстан басқа бір-де-бір жүмыс жүргізілмейді, яғни А = 0.
3. Реакцияға дейінгі және кейінгі заттардың температуралары бірдей, яғни ТІ = Т2.
Термохимияның негізі Гесс заңы болып саналады. Кейде оны реакция жылулары қосындыларының тұрақтылығы туралы заң деп те атайды және ол былайша тұжырымдалады: химиялық реакциялардың жылу эффектісі реакцияға қатысатын және одан алынатын заттардың табиғаты жэне күйімен анықталады да арадағы , сатылай жүретін химиялық реащияларға тәуелсіз, яғни әуелгі күйден соңғыға ауысу әдісіне де байланысты емес.
Реакциялардағы жылу қосындысының тұрақтылығы туралы заңды 1836 -- 1840 жылдарда жүргізген нақтылы тәжірибелері нәтижесінде Петербург университетінің профессоры Г. И. Гесс тұжырымдаған. Жоғарыда келтірілген үш шарттың алғашқы екеуі орындалғанда бұл заңды термодинамикадағы бірінші заңның салдары ретінде қарастыруға болады.
Заттардың жылу эффектілерін, басқа да термодинамикалық функцияларды өзара салыстыру үшін заттардың стандартты күйі жайлы түсінікті енгіземіз. Қатты және сұйық заттардың стандартты күйі ретінде өзін қоршаған ортаның кысымы 1 атм. болған жағдайды қарастырады. Ал, газдар үшін стандартты күй деп олардың 1 атм. қысымдағы идеал газдың күйі қабылданады. Кейбір жағдайларда бұл күй нақты газ күйінен өзгеше болады. Мысалы, 25°С-тағы су буының стандартты күйі гипотетикалық болып есептеледі, өйткені осы 25°С-де қаныққан будың қысымы 0,0312 атм. және оны осы температурада кысып, бір атмосфераға жеткізу мүмкін емес.
Термодинамикалық функциялардың тәжірибе кезінде алынған мағынасынан стандарттығы және керісінше есептегенде газдың 1 атм. қысымдағы және 25°С темпераурадағы мәнінің осындай жағдайдағы идеал газдан ерекше болатынын ескерген жөн. Ол үшін кез келген немесе берілген температурадағы стандартты күй қабылданады. Әдетте, анықтамалықтарда термодинамикалық функциялардың мәні 25°С немесе 298, 15 К берілген,
Судың түзілу реакциясын алайық:
Н2 + 0,5О2 = Н2О (с) = -68,315 ккалмоль
Н2 + 0,502 = Н2О (бу) = - 57,796 ккалмоль.
Мұндағы энтальпияның дәреже көрсеткішіндегі ° оның стандартты екенін көрсетсе, индексіндегі 298 Кельвин температурасын, яғни абсолюттік температураны көрсетеді. Бұл жазулардан, сутектің бір молі мен оттектің жарты молі стандартты күйде алынып, олардан сұйық және бу күйіндегі бір моль су молекуласы түзіліп, өздеріне тән жылу эффектілерімен сипатталғаны көрінеді. Мұндағы кейбір шамалы ғана айырмашылық стандартты күй бірдей болса да, бірі сұйық та, екіншісі бу болып (газ) келетін фазалық айырмашылықта. Жоғарыда келтірілген су буының гипотетикалық айырмашылығы р = 0,0312 атм., оның идеал газдікінен айырмашылығы шамалы.
Реакция жылуын жазудың екі әдісі бар және оларға сәйкес белгілеудің де екі түрі белгілі. Біз мұнан былай термодинамикалық түр деген ұғымды қолданамыз. Бұрын да айтылғандай система жылуды өзіне қабылдаса, онда жылу оң делінеді. Кейбір оқулықтар мен құралдарда термохимиялық деп аталатыи түр колданылады және ондағы пікірге сәйкес системадан жылу бөлінсе, ол оң делінеді. Бұл түрдегі реакция теңдеуі, төмендегідей жазылады:
С6Н6 (с)+7,5О2 (г)=6СО2 + ЗН2О (с)+780,98 ккал.
Термодинамикалық жүйеде химиялык реакция теңдеуіне реакцияға түсетін және одан алынған реагенттердің ішкі энергиясы немесе энтальпияларының айырмасының шамасы тіркеліп жазылады:
С6Н6 (с) +7,5О2 (г)=6СО2 + ЗН2О (с); Q = = +780,98 ккал.
Реакция теңдеулерінде (қ) -- қатты, (кр) -- кристалды, (с) -- -сұйық, (г) -- газ деген белгілермен заттардың агрегаттық күйі көрсетілген. Кейде системадағы заттардың қысымы, концентрациясы қосымша белгіленеді. Сол сияқты химиялық реакциялардың. жылу эффектілерін сипаттағанда, ішкі энергиядан гөрі энтальпия мөлшері жиірек пайдаланылады.
Гесс заңының практикадағы қолданбалы маңызы өте зор. Оның көмегімен әлі белгісіз, бірақ есептеу үшін не басқа мақсатқа қажет болатын реакциялардың жылу эффектілерін есептеуге болады. Бұл жағдайда есептейтін реакцияларға жанама, қосымша, бірақ жылу эффектілері белгілі реакциялар пайдаланылады. Айталық, С + 0,5О2 = СО және С + СО2 = 2СО сияқты жүруі мен анықтауы, өлшеуі мен есептеуі аса қиын реакциялардың жылу эффектілерін есептеу керек болсын, оны анықтау үшін белгілі деректерді қосымша ретінде пайдаланамыз. Мынадай есепті шығарайық:
1) С (гр)+О2 = СО2; =-94052 кал;
2) СО + 0,5 О2 = СО2; = -67640 кал реакциялары үшін ΔH° табу керек:
3) С (гр)+0,5О2 = СО; = ?
4) С (гр)+С02 = 2СО; = ?
Ол үшін қолдағы бар деректерді пайдаланып көміртек (IV) оксидінің түзілу схемасын жасайық (4, а-сурет). \

Гесс заңына орай Жылу эффектілерімен жүргізілген амалдар да нақ осыны берері даусыз.
= 94052- (-67640) = -26412 кал.
4-теңдеуді табу үшін, 1-ден 2-ні алып, сол айырманы теңдеу алдындағы коэффициентке сәйкес екі еселеу қажет:

Жалпы түрдегі процестердің өзгеруі 4, б-суретте келтірілген. Берілген А1, А2, А3, ... заттар реакцияласып В1 В2, В3, ... түзеді. Бұл реакция үш түрлі жолмен (әдіспен) жүруі мүмкін: ол біріншіден тікелей түрленуі мүмкін, мұндайда реакцияның жылу эффектісі ΔΗ1-ге тең; екіншіден, 2, 3, 4-сатылары арқылы жүруі мүмкін, мұндағы жылу эффектісі ΔΗ2, ΔΗ3 және ΔΗ4 қосындысы-на теңеледі, ал 5, 6, 7 және 8-сатылары арқылы жүрген реакцияның, жалпы жылу эффектісі осы реакциялардың жылу эффектілерінің қосындысына тең. Гесс заңына сүйеніп, ондағы жылу эффектілерінің өзара қатынастағы байланысын пайдалансақ:

Көптеген химиялық құбылыстар мен қосылыстар химиялық реакция нәтижесінде жүзеге асады. Ал, химиялық реакциялар өз сипатына байланысты бірнеше түрге жіктеледі. Олардың бәрі жылумен тікелей байланысты, өйткені әрбір химиялық реакция жүрген кезде, мейлі олар бір қосылысты алу, тотықтыру, ыдырату, нейтралдау болсын, бәрі бір олардың әрқайсысы жылу бөледі, не сіңіреді. Тіпті қышқыл, негіз, түз және басқаларды еріткенде де жылу құбылыстары байқалады.
Белгілі жағдайда екі не үш химиялық элемент немесе қосылыс өзара реакцияласуы нәтижесінде пайда болатын жылу мейлі ол сіңіру не шығару жылуы болсын, түзілу жылуы болады. Түзілу жылуы дегеніміз көрсетілген жағдайда, берілген заттардан (реакцияға түсетін зат) реакция нәтижесінде бір моль өнім алынатын реакцияның жылу эффектісі. Түзілу жылуы оң және теріс мәнді болады. Жай заттардың түзілу жылуы нөлге тең.
Химиялық реакциялардың жылу эффектісі реакция нәтижесінде алынатын өнім мен реакцияға түсетін заттардың, (реагенттердің) ішкі энергияларының айырмасына тең:

Жану дегеніміз де химиялық реакция, яғни кез келген химиялық элементтің немесе қосылыстың, тіпті күрделі заттың оттекпен әрекеттесуі. Әрине, бұл химиялық реакцияны тотығу реакциясы дейді, оның салдарынан оксид және көптеген жылу бөлінеді. Жану жылуы деп берілген элемент не күрделі қосылыстың оттекпен әрекеттесуі кезінде оларға сәйкес жоғары оксид түзілетін реакциялардың жылу эффектісін айтады. Органикалық қосылыстар оттекпен әрекеттескенде көміртек (IV) оксидін және сұйық не бу (газ) күйіндегі су, кейде оның құрамында шамалы болса да күкірт, азот, фосфор сияқты элементтер болса, онда соларға сәйкес оксидтер түзіледі. Егер оксидтер құрамында инертті газдар, басқа да қосылыстар кездессе, олар жайлы арнайы ескерту айтылады. Жану жылуын сәтті пайдаланып, көптеген химиялық реакцияның жылу-ын есептеуге болады. Ал, жану жылуын пайдаланып, химиялык реакцияның жылу эффектісін есептеуге Гесс заңы қолданылады, оған бірер мысал келтірейік.
(СООН)2 (қ)+2 СН3ОН (с) = (СООСН3)2 (с)+2 Н2О (с)
Катты күйдегі қымыздық қышқылы метил спиртімен әрекеттесіп, эфир және су түзеді. Енді осы реакцияның жылу эффектісін есептеу керек. Ол үшін реакцияға қатысатын әрбір қосылыстың жану жылуын табамыз:
1. (СООН)2 (қ)+0,502 (г)=2СО (г)+Н2О (с); ΔН1 = -- 60,1 ккал;
2. 2СН3ОН (с)+302 (г)=2С02 (г)+4Н20 (с); ΔНІІ = -- 347,3 ккал;
3. (СООС3Н)2 (с) + 3,502 (г)=2СО2 (г)+ЗН2О (с); ΔНІІІ = -- 401,0 ккал.
Гесс заңына жүгінсек, реакцияның жылу эффектісі:
ΔΗ=ΔΗI + ΔΗII + ΔΗIII =-60,1-347,3 + 401,0=-6,4 ккал
Идеал газдың ұлғаю жұмысы. Менделеев-Клапейрон теңдеуімен күйін ернектеуге болатын газды идеал газ дейді. Ол ішкі энергиясы температураға тәуелді, қысым мен көлемге тәуелсіз газдар туралы түжырымдалған Гей-Люссак-Джоуль заңына бағынады. Қысым мен көлем ішкі энергияға ешбір өзгеріс енгізбесе, онда жұмыс газдың ұлғаюы кезінде ғана жүреді. Оны бұл топтағы газдармен тығыз байланысы бар кейбір құбылыстарға арнап, термодинамиканың бірінші заңымен ұштастырып, қолдануға болады.
Газ көлемі ұлғайғанда шамалы болса да жұмыс істеледі. Жұмыстың мөлшері термодинамикалық процесті жүргізу түрі мен әдісіне, жағдайына, сондай-ақ газ көлемінің өзгерісіне байланысты. Ал газ ауасыз, кедергісіз бос орынға ауысса ешбір жұмыссыз-ақ, бос орынды толтырады. Ендеше, газ ұлғаю кезінде жұмыс пайда болу үшін міндетті түрде кедергіге кездесуі керек екен, яғни газ ұлғаю кезінде кездесетін кедергі көбейген сайын, мұның нәтижесінде алынатын жұмыс та артады.
Гей-Люссак-Джоуль заңы тәжірибе негізінде тұжырымдалса да, оны теориялық тұрғыдан қарастырып, термодинамиканың екінші заңы арқылы дәлелдеуте болады. 1809 жылы Гей-Люссак және 1844 жылы Джоуль көптеген тәжірибе жүргізді. Олардың қысқаша мазмұны мынадай: Шүмегі бар түтік арқылы жалғасқан екі баллон су құйылған ыдыс ішіне орналасқан. Судың температурасы термометрмен өлшенеді. Баллонның біреуінің ішіндегі газдың кысымы р1, ал екіншісі бос, демек р2 = 0. Егер шүмекті ашсақ, газ бос баллонға ауысады. Осы сәтте бірінші баллон салқындаса, екінші баллон жылынады. Ал газ қысымы теңелген соң, судың температурасы өзінің, тәжірибеге дейінгі мәніне қайта келеді. Ендеше, екеуіндегі қысым да, көлем де бірдей, мұндайда ешбір жұмыс істелмейді, яғни олардың ішкі энергиясы да, жұмыс та нөлге тең. Бұл айтылғандардың бәрі термодинамиканың бірінші заңымен толық үндестік табады.
Енді көлденең қимасының ауданы S болатын цилиндр ішінде жүретін газдың қайтымды ұлғаюын қарастырайық (5-сурет). Мұндағы система қарсы жұмыс істейтін сыртқы қысымды р, поршеньннің шексіз кішкене биіктікке жылжуын dһ арқылы белгілеп, поршень ешбір кедергісіз қозғалады дейік. Егер поршеньді_ қозғайтын күш қима ауданы мен қысым көбейтіндісіне тең болса (р·S),осы күштің атқарар жұмысы: А = рSdh, немесе Sdһ көлемнің өзгеруіне (dV) тең болғандықтан

Бұл теңдеуді шешу үшін қысымның көлемге тәуелділігін білу керек. Ол үшін изобаралық, изотермалық, адиабаталық және изохоралық процестердегі идеал газдардың жұмысын қарастырайық.
Изобаралық процесте (р = const) системаның қысымы тұрақты, яғни ешбір өзгеріссіз болуы керек. Мұндай жағдайда соңғы (19) теңдеу мына төмендегідей өрнектеледі:
А=ρ(V2V1) (20)

көлем өзгерісінің көбейтіндісіне тең. Жұмыстың көлем өзгерісіне тәуелділігі 6-суретте көрсетілген және ол Ү1ЕFV2 шектелген тік төртбұрыш ауданымен сипатталады. Бір моль газдың ұлғаюын қарастырғанда, жалпы газ күйін өрнектейтін рV = RТ Клапейрон-Менделеев теңдеуіндегі рV1 мен рV2-ні сәйкес RТ1 және RТ2-мен аүыстырып жазсақ:

яғни изобаралық процестің жылуы (QP) энталышяның өзгеруіне тең.
Ал тұйықталған процесте, системадағы ішкі энергияның өзгеруі нөлге тең (ΔU = 0), қысым мен көлем өзгерісінің көбейтіндісі де нөлге тең (Δ(рV)=0) болғандықтан, ондағы энтальпияның да өзгеруі нөлге тең (ΔΗ = 0). Тек система күйіне байланысты болып келетін алгебралық комбинация шамасы күй функциясы деп аталады, олай болса, қарастырылып отырған рV көбейтіндісі де күй функциясы екен.
Изотермалық процесте (T=const) системаның температурасы ешбір өзгеріссіз, тұрақты болып, оның көлемі мен қысымы өзгереді. Мұнда да тұрақты температура кезіндегі бір моль газдың ұлғаю жұмысы идеал газдардың теңдеуі Клапейрон -- Менделеев теңдеуіне тікелей байланыста қарастырылады. Әрине, рV=RТ=р = RТV оны (19) теңдеуге қойсақ, жұмыстың изотермалық процестегі мәнін аламыз:

Осы теңдеуге бағынатын изотермалық процесс нәтижесінде алынатын жұмыс 6-суретте ЕF' қисығымен шектелген V1ЕF'V2 ауданымен өлшенеді: Клапейрон-Менделеев теңдеуінен изотермалық процесте R = соnst, сондықтан RТ = соnst, олай болса қысым мен көлем бір-біріне кері пропорционал екені шығады:

Осы айтылғандарды қысқаша қорытқанда, изотермалық процестегі газдың ұлғаю жұмысы тек көлем мен қысымның кері пропорционалдық жағдайындағы өзгеруіне тәуелді екен және ол жұмыс системаға сырттан енгізілген жылу есебінен жүреді. Демек, системаның температурасы неғүрлым төмен болса, жұмыс солғұрлым аз.
Изохоралық процесте (V=соnst) тек қысым мен температура ғана өзгереді. Бірақ газ күйін сипаттайтын теңдеулерде кездесетін көлем мен қысым көбейтіндісі (рV) тұрақты, өйткені процесс жағдайына байланысты көлем тұрақты. Ендеше және ішкі энергия өзгерісі ондағы жылуға тең, ΔUV=QV, яғни системаға сырттан берілген жылудың бәрі тек системаның ішкі энергиясын арттыруға жұмсалады. Мұндағы жылу Q[V] ішкі энергия UV өлшемі және бұл процесте ешбір жұмыс жүргізілуі мүмкін емес.
Адиабаталық процестегі (Q = 0) газдың үлғаю жұмысы температура мен қысым өзгерген кезде жүреді. Мұнда көлем тұрақты, өзгеріссіз қалады. Газ сырттан, өзге системадан ешбір жылу алмағандықтан (Q = 0), адиабаталық процестегі система жұмысы ондағы идеал газдың ішкі энергиясы есебінен жүргізіледі, ал газдың өзі салқындайды. Жоғарыда келтірген идеал газ күйін сипаттайтын теңдеуден (рV=RТ) идеал газдың ішкі энергиясы тек температураға тәуелді екені көрінеді. Осыны негіз етіп алғанда, системадағы ішкі энергияның өзгерісі ΔU тұрақты көлем кезіндегі жылу сыйымдылығын (СV) температура өзгерісіне (ΔT) көбейткенге тең. Сондықтан да адиабаталық процестегі газдың ұлғаюы кезінде температура төмендеп, система салқындайды. Мұндағы жұмысты жылу сыйымдылығы мен температура өзгерісі арқылы өрнектесек:
A=CV(T1T2) (27)
мүндағы СV -- тұрақты көлем кезіндегі газдың жылу сыйымдылығы. Жылу сыйымдылығы (С) -- заттың бірлік массасын 1 К-ге қыздыруға кеткен жылу мөлшері (өлшемі Джмоль К)). Жылу сыйымдылығы меншікті және молярлі деп бөлінеді.
Қыздыру не суыту жағдайына қарай жылу сыйымдылығы тұрақты көлемдегі (СV), түрақты қысымдағы (Ср) деп қарастырылады.
Адиабаталық процесс 6-суреттегі ЕF" қисығымен көрсетіліп, оның жұмысы V1EFV2 ауданымен анықталады. Ал, осы процестегі жұмысты термодинамиканың бірінші заңы тұрғысынан алып қарастырсақ, осы жұмыстың ішкі энергияның өзгеруі есебінен жүретіні байқалады. Мұндай процестегі жұмыс пен ішкі энергия өзгерісі өзара тең және олардың абсолюттік мәні кері (A = ΔU). Идеал газ үшін:

мұндағы n -- идеал газдың мольдік саны; dT=T1T2; ρdV=A. Жылу сыйымдылығы денеге енген шексіз аз мөлшердегі жылудың осы жылу ену нәтижесінде пайда болатын өзгеріске қатынасымен анықталады. Изохоралық процестер үшін:

Бұл теңдеудің екеуін де барлық агрегаттық күй және барлық заттар үшін қолдануға болады.
Жылу эффектісі және температура. Жылу эффектісі мен температура бір-біріне өте жақын ұғымдар. Олардың арасындағы негізгі байланысты анықтап, жылу эффектісінің температураға тәуелділігін көрсететін теңдеуді тұжырымдау үшін мына теңдеулерді пайдаланамыз:

Өрнектегі U1 және Н1 реагенттердің ішкі энергиясы мен энтальпиясы, ал U2 және H2 өнімнің ішкі энергиясы мен энтальпиясы. Реакция кезіндегі системаның жылу эффектісінің температураға тәуелділігін анықтау үшін осы теңдеулерді температура бойынша дифференциалдау керек:

(29) мен (30) теңдеулерде тұрақты қысым мен көлемдегі жылу сыйымдылығының температураға тәуелділігі берілген. Сол сияқты этальпияның мәнін көрсететін (9) теңдеуде қысым тұрақты болса, онда рV де тұақты болады:

Системаның жылу сыйымдылығы, сол система құрамына енетін компоненттердің жылу сыйымдылықтарының қосындысына тең:

мұндағы ni -- і компонентіндегі моль саны; СV -- молярлі изохоралық жылу сыйымдылығы: Ср -- молярлі изобаралық жылу сыйымдылығы. Егер (31) теңдеуге (29), (30) және (33) теқдеулерде берілген мәндерді қойса, жоғарыда келтірілген пікірлерді қорытындылайтын теңдеу алынады:

Мұнан әрі, (34) теңдеуді Т1 және Т2 температуралық интервалында интегралдасақ:

Бұл Кирхгоф теңдеуі деп аталады, да , оның математикалық тұжырымдамасы Кирхгоф заңы делінеді: реакциялардың жылу эффектісінің температуралық коэффициенті (dQdT) реакцияға түсетін заттардың соңғы және әуелгі күйдегі жылу эффектілерінің қосындыларының айырмасына тең. Егер химиялық реакцияның Т1 температурадағы жылу эффектілері (QV және QP) белгілі болса,олардың Т2 температурадағы мәндерін табу үшін (35) теңдеудегі интегралдың оң жақтағы бөлігін интегралдан шығарады. Ал реакция теңдеуіндегі химиялық қосылыстар алдында тұратын коэффициентті пайдаланып, мольдік шаманы көрсететін стехиметриялық коэффициентті (ni) табуға болады. Олай болса, химиялық реакциялардың жылу эффектілерінің температураға тәуелділігін табу дегеніміз белгілі интегралдарды таза математикалық тұрғыдан есептеп шығару керек.
Химиялық реакциялардың немесе термодинамикалық системалардың жылу эффектілері температураға тәуелді бола бермейді. Ендеше температуралық интервал аса көп болмаса, яғни бірнеше ондаған градустан аспаса және ол өте бір дәлдікпен анықтауды керек етпесе, онда интеграл астында тұрған барлық жылу сыйымдылықтарын тұрақты деуге болады. ал, температуралық интервал біршама көп болып және едәуір дәлдік қажет болса, жылу сыйымдылығының температураға тәуелділігін ескеру керек. Кирхгоф заңын мына төмендегі өрнекпен де көрсетуге болады:

(36)
Т2 - Т1 температуралық интервалында изохоралық жылу сыйымдылығы СV мен изобаралық жылу сыйымдылығы СР температураға тәуелсіз деп, осы өрнекті интегралдасақ:

(37)
Едәір дәлдікпен есептеу кезінде барлық жылу сыйымдылықтарының температураға тәуелділігін есептеу шұбалаңқы шығады, бірақ оның мәні қарапайым қалады. Жылу сыйымдылығының температураға тәуелділігі шамалы қатынаста қабылдайды:
(38)
Бұл теңдеулердегі а0, а1, а2 және а2[-2] коэффициенттері анықтамалықтарда берілген. Таблицада, әдетте коэффициенттердің мәні ғана келтіріледі. Егер ол мән Ср үшін болса, онда (36) теңдеуден екінші формуланы пайдаланамыз. Ал, ішкі энергия (ΔU) мәнін табу керек болса, онда катты және сұйық заттар үшін Ср≈ Сv екенін, ал газдар үшін Сv = Сp -- R екенін ескеру керек. Қейде жоғарғы теңдеуді (36) теңдеуге қойсақ, (38) теңдеуге қатынасты жылу сыйымдылықтарының бір бөлігі ауысып, кері де болуы мүмкін. Сондықтан, а2Т[2] және а-2Т[-2] сияқты белгілерді интеграл астына енгізсек, (әр түрлі затқа қатынасы бар а2 немесе а-2 коэффициенттер нөлге тең:

Кирхгоф формуласы сұйық заттардың булану жылуының температураға байланысын көрсетіп, оны есептеуге мүмкіндік береді. Алайда кейбір қосымша шарттардың, орындалуы талап етіледі. Мысалы, екі температура арасындағы жылу эффектісін есептеу керек болсын. Т1 температурасының жылу эффектісі белгілі жағдайда Т2 температурасының жылу эффектісін есептеп шығару үшін, осы Т2 температурадағы компоненттердің қысымы әуелгі Т1 температурадағы қысымға тән болуы керек. Температура өзгергенде қысым тұрақты болса, фазалық ауысу болмайды, бұл оның химиялық реакциядан өзгешелігін көрсетеді. Алайда, фазалық ауысу кезіндегі қысым мен температура өзара байланысты болғандықтан, әрбір фазалық тепе-теңдік жағдайындағы жылу сыйымдылығы Ср, сондай-ақ СV шамаларынан өзгеше болады. Әйтсе де Кирхгоф формуласы мұны да шамамен есептеуге ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.