Қашықтықтан оқыту жағдайында 7-сыныпта математикадан олимпиадалық есептерді шешу электрондық факультативтік курсын әзірлеу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 56 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

А. Байтұрсынов атындағы Қостанай өңірлік университеті

«Қорғауға жіберіледі»

Математика кафедрасы

А. Утемисова

«___» 2021ж.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Қашықтықтан оқыту жағдайында «7-сыныпта математикадан олимпиадалық есептерді шешу»электрондық факультативтік курсын әзірлеу

5В010900-Математика мамандығы

Орындаған :

А. Дүйсенбай, күндізгі оқу нысанының 4 курс студенті

Орындаған:: Ғылыми жетекші :

А. Дүйсенбай, күндізгі оқунысанының 4 курс студенті: ф. -м. ғ. к., доцент Р. Ысмагул

Қостанай, 2022

Мазмұны

Кіріспе . . .

Кіріспе . . .: 1

3: Функцияны зерттеуге арналған есептерді шығаруды оқыту әдістемесі . . .

Кіріспе . . .: 1. 1

3: Математикадағы функция ұғымының даму тарихы . . .

Кіріспе . . .: 1. 2

3: Функция, оның қасиеттері және графигі . . .

Кіріспе . . .: 1. 3

3: Элементар функциялардың анықталу облысы мен мәндерінің облысы . . .

Кіріспе . . .: 1. 4

3: Негізгі мектеп курсында функцияларды зерттеудің әдістемелік схемасы . . .

Кіріспе . . .: 1. 5

3: Негізгі мектеп бағдарламасындағы және мектептің математика оқулықтарындағы функцияны зерттеуге арналған есептер . . .

Кіріспе . . .: 2

3: Практикалық бөлім . . .

Кіріспе . . .: 2. 1

3: 10-сыныпта функцияны зерттеу және графигін салуға арналған есептерді шығаруды оқытуға нұсқаулық . . .

Кіріспе . . .: 2. 2

3: 10 «В» сыныбына жүргізілген педагогикалық сараптама . . .

Кіріспе . . .: Қорытынды . . .

3: 56

Кіріспе . . .: Пайдаланылған әдебиеттер тізімі . . .

3: 57

Кіріспе

Қазақтың тұңғыш ғалымы Шоқан Уәлихановтың «Халықтың кемеліне келіп, өркендеп өсуі үшін ең алдымен азаттық пен білім қажет» деп айтқан қанатты сөзі бүгінгі тәуелсіз еліміздің жастары үшін болашаққа бастау мұраты болмақ. Бұлай дейтініміз, қазіргі қарыштап дамып жатқан әлем өркениетінің негізі сапалы оқу-біліммен тығыз байланысты екендігі баршамызға аян. Бұл мәселе Елбасы Жолдауында назардан тыс қалмаған. Тұңғыш Елбасымыз Н. Ә. Назарбаевтың Қазақстан халқына жолдауында: «Ұлттық бәсекелестік қабілеті бірінші кезекте оның білімдік деңгейімен айқындалады» деп айтылған. [1]

«Есепті жеңу - ой жеңісі» болып табылады.

Дипломдық жұмыстың өзектілігі: Математиканы оқыту барысында оқушылардың дайындықтарының тиімділігі мен білімдерінің сапасы дәстүрлі емес тұрпаттар, әдістер мен тәсілдер жүйесін құру арқылы жүзеге асырылуы мүмкін, сондықтан әдістемелік нұсқаулықтарды қолданып, функцияны зерттеуге арналған есептерді шығару өзекті мәселелердің бірі болып табылады.

Дипломдық жұмыстың мақсаты: Функцияны зерттеуге арналған есептерді шешуді оқыту әдістемесін зерделеп, әдістемелік нұсқаулық құру және оны практикада қолданылуын құрастырып, сараптама жүргізу.

Дипломдық жұмыстың міндеттері:

-функцияны зерттеуге арналған есептерді шығару әдістемесінің теориялық негіздерін зерделеу;

- орта мектеп бағдарламасындағы оқулықтарға талдау жүргізу;

- 10-сыныпта функцияны зерттеуге арналған есептерді шығаруды оқыту әдістемесі бойынша нұсқаулық дайындау;

- гипотезаны тексеруге бағытталған сараптаманы өткізу.

Зерттеу объектісі: Функцияны зерттеуге арналған есептер.

Зерттеу пәні: 10 сынып оқушыларының функцияны зерттеуге арналған есептерді шығару процесінде оқу қызметі.

Жаңашылдығы: Функцияны зерттеуге арналған есептердішығару әдістемесінің теориялық негіздері жүйелі зерделеніп, әдістемелік нұсқаулық құрастыру арқылы практикалық бөлімнің құрылуы болып табылады.

Тәжірибелік маңызы: Дипломдық жұмыс педагогикалық институттардың және университеттердің математика мамандығын таңдаған студенттер үшін машықтанудан өткенде, факультатив сабақтарын өткізгенде әдістемелік жәрдемші болады.

Ғылыми болжам: егер 10-шы сынып оқушылары функцияны зерттеуге арналған есептерді шығару үшін қосымша құрал ретінде әдістемелік нұсқаулығын қолданса, онда олардың танымдылық белсенділіктері мен қызығушылықтары артады және оқу үлгерімі жоғарылайды.

1 Функцияны зерттеуге арналған есептерді шығарудың оқыту әдістемесі

1. 1 Математикадағы функция ұғымының даму тарихы

Әлемді тануда функция ұғымы үлкен рөл атқарады.

Шамалар арасындағы алғашқы математикалық қатынастардан, сандарға қолданылатын алғашқы ережелерден, фигуралардың ауданы мен көлемін табудың алғашқы формулаларынан орын алған функционалдық тәуелділік осы идеяның (функцияның) ертеден бастау алғанын білдіреді.

Математикаға айнымалы шама ұғымының енгізілуімен XVII ғ. функционалдық тәуелділікті қолдану және оны зерттеу басталды.

Ол кезде функция ұғымы анық берілген жоқ, дегенмен функцияның алғашқы анықтамасын Р. Декарт «Геометрия» атты еңбегінде ұсынды. Бұл еңбегінде ол алгебралық теңдеулер көмегімен ғана дәл бейнеленетін қисықтарды қарастырды.

Біртіндеп функция ұғымы оның аналитикалық сипаттамасы - формуламен теңесті.

Функция сөзін (лат. functio - «аяқтау, орындау») Г. В. Лейбниц берілген немесе басқа бір міндетті орындаушы шама мағынасында қолданды.

« x- тен функция» терминін алғаш Г. В. Лейбниц «айнымалы» және «константа» (тұрақты) терминдерін енгізді.

1718 ж. швейцариялық математик И. Бернулли функцияға дәлірек анықтама берді: « Айнымалы шаманың функциясы деп осы айнымалы мен тұрақтыдан қандай да бір тәсілмен құрылған шаманы айтады ».

Л. Эйлер «Анализге кіріспе» (1748 ж. ) атты кітабында функцияның анықтамасын былай тұжырымдайды: « Айнымалы шаманың функциясы дегеніміз - осы айнымалы шама мен сандардан немесе тұрақты шамадан құрылған аналитикалық өрнек ».

Л. Эйлер қазіргі кезде қолданған функцияның белгілеулерін енгізген.

Функцияның берілу тәсілі қолданылмайтын сандық функцияның қазіргі анықтамасын орыс математигі Н. И. Лобачевский (1834 ж. ) мен неміс математигі П. Дирихле (1837 ж. ) бір-біріне тәуелсіз берген.

Функцияның математикалық тұжырымдамасы бір шаманың басқа шаманың мәнін қалай толық анықтайтындығы туралы интуитивті түсінікті білдіреді. Сонымен, $x\$ айнымалы мәні $x^{2\ }$ өрнегінің мәнін анықтайды, сонымен қатар айдың мәні келесі айдың мәнін нақты анықтайды. Функцияның тағы бір мысалы:әр адам өзінің биологиялық анасымен ерекше байланыста бола алады.

Сол сияқты, кіріс деректерінің мәні бойынша алдын-ала жасалған алгоритм шығыс деректерінің мәнін береді.

Бұл анықтамалардың негізгі мағынасы мынадай: «Егер х- тің әрбір мәніне y- тің белгілі бір мәні сәйкес келсе, онда y бұл сәйкестіктің формуламен, графикпен, кесте түрінде немесе сөзбен берілгеніне қарамастан, x айнымалысының ( $a \leq x \leq b$ кесіндісінде) функциясы болады.

Анықталу облысы мен мәндер жиыны таңдап алынатын қазіргі кездегі функция туралы түсінік XX ғ. бірінші жартысында жиындар теориясын жасаған Г. Кантордың (1845-1918) еңбегінде тұжырымдалды. Жаңа абстрактілі ұғымды енгізу қажеттілігін түсіну үшін көптеген нақты есептерді шығару барысында осы ұғымды бөліп алып және оның мағынасын мүмкіндігінше дәл бейнелейтін анықтама беру қажет.

Жаратылыстану және басқа да ғылымдарда ашылып жатқан жаңалықтар функция ұғымының ғана емес, басқа да математикалық ұғымдардың дамуына жол ашады.

Көбінесе"функция" термині сандық функция деп түсініледі, яғни кейбір сандарды басқаларына сәйкестендіретін функция. Бұл функциялар графиктер түрінде ыңғайлы. [3]

Мысалы: $f(x) = \frac{({4x}^{3} - {6x}^{2} + 1) \sqrt{x + 1}}{3 - x}$ функциясының графигі (1 суретке қараңыз) .

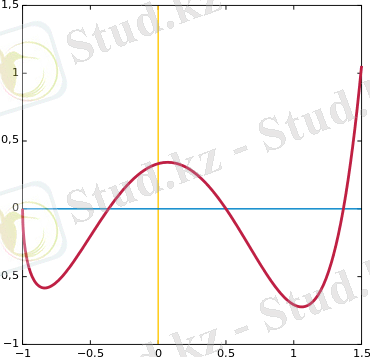
1 сурет - $f(x) = \frac{({4x}^{3} - {6x}^{2} + 1) \sqrt{x + 1}}{3 - x}$ функциясының графигі.

"Функция" терминін (біршама тар мағынада) алғаш рет Лейбниц қолданған (1692) . Өз кезегінде Иоганн Бернулли сол Лейбницке жазған хатында бұл терминді қазіргі заманға жақын мағынада қолданды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.