Функция туындысын теңсіздіктер дәлелдеуде қолдану

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

Ақтөбе облыстық мамандандырылған
физика-математикалық мектеп-интернаты

Жобаның тақырыбы:
Функция туындысын теңсіздіктер дәлелдеуде қолдану

Секция: математика

Орындаушылар: Нұралықызы Гүлназ
Жеткергенов Шапағат

Жетекшісі: Зейнулла Р.А.
математика пәні мұғалімі

Ғылыми жетекші: А.Е.Иманчиев
Қ.Жұбанов атындағы Ақтөбе өңірлік университеті

математика кафедрасының доценті,
физика-математика ғылымдарының
кандидаты

Ақтөбе, 2021ж.

МАЗМҰНЫ

КІРІСПЕ 3
1 ТУЫНДЫ ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУЫ 5
1.1 Туынды анықтамасы 5
1.2 Бірінші ретті туынды арқылы тепе - теңдікті дәлелдеу және 7 өрнектерді ықшамдау
1.3 Бірінші ретті туынды арқылы теңсіздікті дәлелдеу 10
1.3 Екінші ретті туындынының көмегімен теңсіздіктерді дәлелдеу 14
1.4 Туындының көмегімен Ньютон биномының формуласын есептеу 14
1.5 Қиындығы жоғары теңсіздіктерді дәлелдеуге туындыны қолдану
16
Қорытынды 43

КІРІСПЕ

Туынды термині derivee деген француз сөзінің қазақша сөзбе-сөз аудармасы, оны 1797 ж. Ж. Лагранж (1736 - 1813) енгізген, қазіргі кездегі 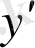, 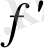белгілеулерін де сол енгізген. Бұл атау мынадай ұғымның мағынасын ашады: 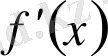функциясы 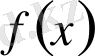- тен шығады, 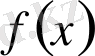- тің туындысы болып табылады.
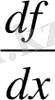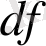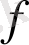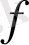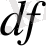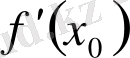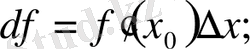
И. Ньютон функцияның туындысын флюксия деп, ал функцияның өзін флюента деп атаған. Г. Лейбниц дифференциалдық қатынас туралы айтқан және туындыны түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиі кездеседі. Лейбниц символын функциясының дифференциалын белгілеу үшін таңдап алған. функциясының дифференциалы - туындысының өсімшесіне көбейтіндісі, яғни белгілеуін 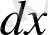-пен алмастырып, оны былай да жазуға болады: 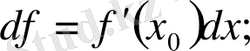осыдан .
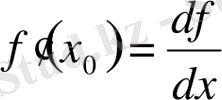Жұмыстың зерттеу нысаны: Математиканы тереңдетіп оқытудағы туындының алгебралық қолданысын, пәнаралық байланысын оқып үйрену.
Мақсаты - математиканы тереңдетіп оқитын сыныптарда туындының алгебралық қолданылуына түсінік беру. Математикалық модельдеудің әдiстерін меңгеру.
Туынды және оны теңсіздіктер дәлелдеуде қолдану тақырыбында функцияларды зерттеу мен кейбір физика есептерін шешуге арналған нұсқаулар ғана көрініс береді. Ал, шынында туындыны қолданып тепе - теңдіктерді, теңдеулер мен теңсіздіктерді шешуге, өрнектерді ықшамдауға болады. Тереңдетіп оқытатын сыныптарда оқушылардың жалпы математикадан дайындық деңгейін арттыра түсудегі туындыны алгебрада кеңінен пайдаланудың дидактикалық құндылығының маңызы зор.
Математиканың көптеген абстрактілі теориялары мен негізгі принциптерінің жаратылыстану ғылымдарының маңызды мәселелерін шешуге қолдану жолдары математиканың бір ірі бөлігі - туынды арқылы жүзеге асады. Туындының көмегімен жаратылыстану ғылымдарындағы ең негізгі проблеманың бірі өзімізді қоршап тұрған табиғат құбылыстарының кейбір жасырын сырының қалай ашылғанын, оның өмірде қалай пайдаланылатынын көрсетуге болады.
Міндеттері:
o Туындының қолданылуы туралы түсінік беру;
o туындының алгебралық қолданылуын оқып үйрену, меңгеру және оны қолдана білуге дағдыландыру;
o математикалық модельдеудің әдiстерін меңгеру мен пәнаралық байланыстарды жүзеге асыру.
Гипотеза
Туынды - математикалық талдаудың негізгі түсінігі болып орта мектеп математика курсында да және жоғары математика саласында да орасан зор маңызы бар. Математиканың барлық бөлімі, саласы бір - біріне тұрақты, тіпті басқа пәндермен де байланысы күшті пән. Математика дәл нақтылы білім береді және басқа пәндердің дамуына көмектеседі - деп Әл - Фараби бабамыз босқа айтпаған. Туындының математикада қолданылуы оқушылардың математиканы терең түсінуі үшін ықпалын тигізеді.
Алгебралық әдістерге қарағанда көптеген есептерді туындыны қолданып шешкендегі балама әдіс ретіндегі ұтымдылығын байқау аса қиын мәселе емес. Сондықтан төмендегі мысалдарда, қажетіне қарай, алгебралық есептерді шешудің туындыны қолданған түрін көрсеттік.

1 ТУЫНДЫ ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУЫ
1.1 Туынды анықтамасы
Кез келген f функциясы жіне оның анықталу обылысының кез - келген х0 нүктесі төмендегідей түрде сипатталуы мүмкін.
1. f функциясын анықтайтын формулалар арқылы оның х0 нүктесіндегі өсімшесін табамыз:
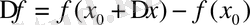
2. Айырымдық қатынас 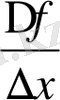үшін өрнек жазамыз:

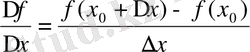
Сонан соң оны түрлендіріп ықшамдаймыз, -ке қысқартамыз және т.с.с.
3. Егер нөлге ұмтылады деп есептесек 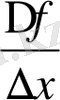қандай санға ұмтылатынын айқындаймыз.
Осылайша табылған санды кейде, физикадағы сияқты, х0 нүктесіндегі 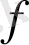функцияның жылдамдығының өзгеруі немесе 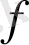функцияның х0 нүктесіндегі туындысы деп атайды.
Анықтама: 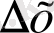нөлге ұмтылғанда функция өсімшесінің аргументтің өсімшесіне қатынасы ұмтылатын сан 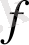функцияның х0 нүктесіндегі туындысы деп аталады.
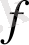функцисының х0 нүктесіндегі туындысы 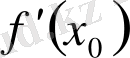деп белгіленеді (х0-ден эф штрих деп оқылады):

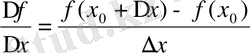
Мысал 1. 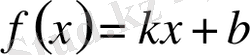( k мен b тұрақтылар) функцияның х0 нүктесіндегі туындысын табайық.
1) .
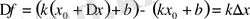2)
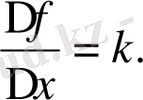
3) k - тұрақты, 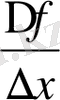саны кез келген үшінші тұрақты, демек
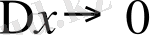
Болса
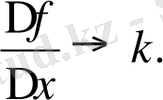
Сөйтіп, .
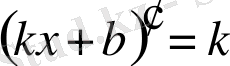х0 нүктесінде туындысы бар функция осы нүктеде дифференциалданатын функция деп аталады. Айталық, D1- функция дифференциалданатын нүктелердің жиыны болсын. Әрбір 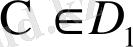санына 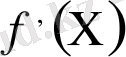санын сәйкес қойа отырып, анықталу обылысы D1 болатын жаңа функция аламыз. Бұл функция 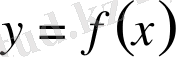функциясының туындысы деп аталады да, 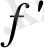немесе 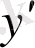деп белгіленеді.
Берілген 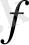функциясының туындысын табу дифференциалдау деп аталады.
Біз бұл бапта мынадай дифференциалдау формулаларын алдық:

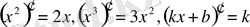
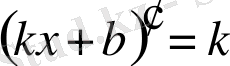формаласында k=0, b=C (C-еркімізше алынған тұрақты) деп ұйғырсақ, 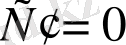екені шығады, яғни тұрақтының туындысы нөлге тең.
1.2 Бірінші ретті туынды арқылы тепе - теңдікті дәлелдеу және өрнектерді ықшамдау
Егер қандайда бір І аралығында 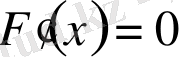болса, онда 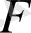функциясы осы аралықта тұрақты шама болады.
Тепе - теңдіктер әдетте 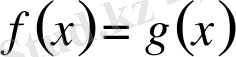түрінде берілетіндіктен бұл теореманы сәл өзгертіп аламыз.
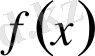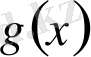Егер және функцияларының туындылары І аралығының әрбір нүктесінде өзара тең болса, онда осы аралықта функциялардың айырмасы тұрақты.
Тепе - теңдікті дәлелдеу төмендегі алгоритм бойынша жүргізіледі.
1. Берілген тепе - теңдікті 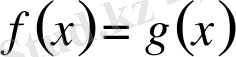түрінде немесе 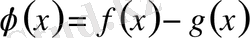түрінде қарастырамыз (анықталу облысы, І аралығында үздіксіздігі)
2. 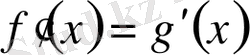немесе 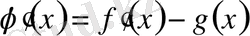түрінде туындыларды табамыз.
3. Егер 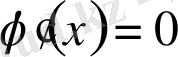болса, онда 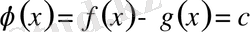болады.
4. Анықталу облысынан 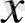үшін есептеуге ыңғайлы бір мәнді алып, 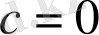яғни 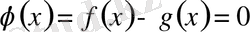екенін дәлелдесек, онда 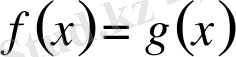болғаны, яғни тепе - теңдікті дәлелдеу аяқталады.
Мысал 2. Тепе - теңдікті дәлелде:
1) ;
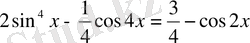Шешуі: 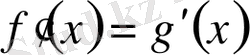түрінде теңдіктің екі жағынан жеке - жеке туынды аламыз.

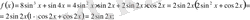
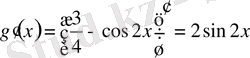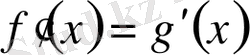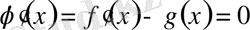; яғни ; Ендеше 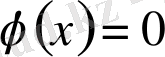; 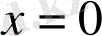болсын, 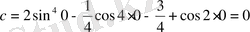; 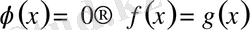. Тепе - теңдік дәлелдеңді.
Туынды арқылы алгебралық және тригонометриялық теңдеулерді түрлендіруге, яғни өрнектерді көбейткіштерге жіктеуге болады.
Мысал 3. Мына өрнекті 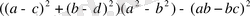көбейткіштерге жіктейік.
-ны айнымалы деп алып өрнекті 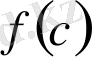функциясы деп алып туындыны табамыз.

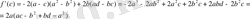
Сондықтан
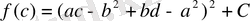
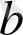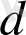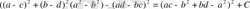
Мұнда , , , параметрлерімен берілген өрнек, бұдан деп алып онда 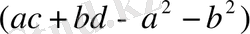өрнекті алғашқы өрнектің шешімі болып табылады.
Мысал 4.
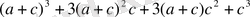
өрнегін көбейткіштерге жіктеп 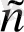-ны айнымалы деп алып, туындыны табамыз.

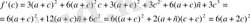
онда
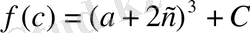
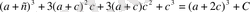
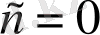деп алсақ, 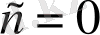, онда 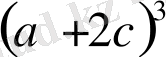өрнегі берілген функцияның шешімі болады.
Мысал 5.
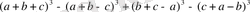
өрнекті деп белгілей отырып

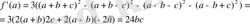
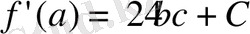
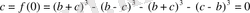
Сонымен берілген өрнектің шешімі .
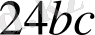1.3 Бірінші ретті туынды арқылы теңсіздікті дәлелдеу
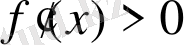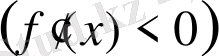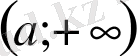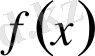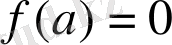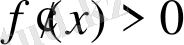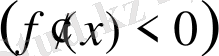Оқулықта интервалдар әдісі арқылы теңсіздіктерді шешу үлгісі көрсетілгенімен, оларды дәлелдеу әдістері келтірілмеген. Сондықтан мына Егер І интервалының әрбір нүктесінде , болса, онда f функциясы І интервалында өседі (кемиді) теоремаға аздаған өзгеріс енгізсек, теңсіздіктерді дәлелдеуге қолайлы тұжырымға келеміз. Егер аралығындағы нүктесінде үздіксіз функциясы үшін және , болса, онда осы аралықта функция оң (теріс) болады.
Шынында да 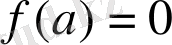, , 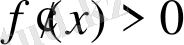және 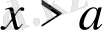болса, онда 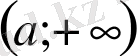аралығында функция өседі, яғни 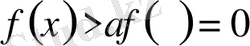демек, .
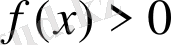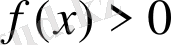яғни функциясының теріс болу жағдайы да осылай дәлелденеді. Осы тұжырымдарды теңсіздіктерді дәлелдеуде туындыны қолдану алгоритмі ретінде қабылдаймыз.
Мысал 6. Дәлелдеңдер: 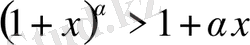, мұнда .
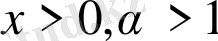Шешуі: 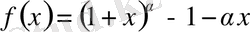функциясын қарастырамыз, мұнда 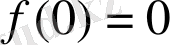, 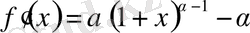шарт бойынша 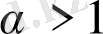болғандықтан 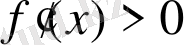. Ендеше 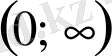аралығында 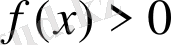демек ; ;
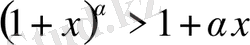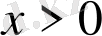Мысал 7. Дәлелдеңдер: , .
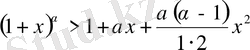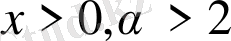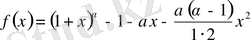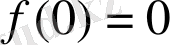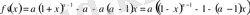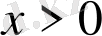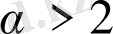
Шешуі: функциясын қарастырамыз, мұнда , . 1 - ші мысалды пайдаланып, және 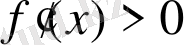болатының білеміз. Сондықтан, жоғарыда айтуымыз бойынша 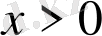болғанда 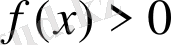болады. Демек,
.
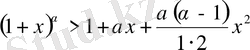Мысал 8. x-тің барлық оң мәндері үшін 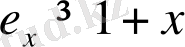, болатының дәлелдеңдер.
Шешуі: 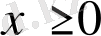үшін 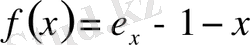функциясын қарастырамыз.
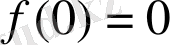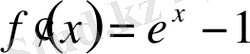; , берілген 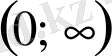аралығында ; 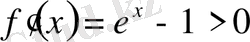; ендеше 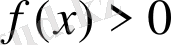, яғни , .
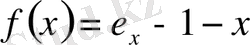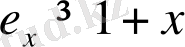Теорема 1. Егер 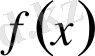, 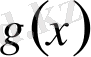функциялары үшін 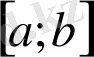да үзіліссіз және туындылары бар және 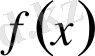, 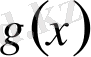өспелі функциялар үшін 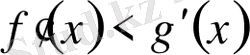шарты орындалатын болса, онда сол интервалда 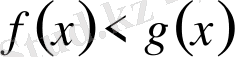шарты да орындалады.
Мысал 9. 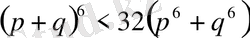теңсіздікті дәлелдеу керек, мұндағы ; ; 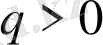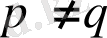болсын делік. 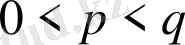болсын. 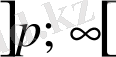- басы 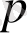оңға бағытталған шексіз аралықта. 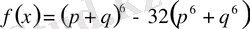функциясының туындысының таңбасын 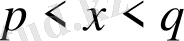болғанда тексерсек, 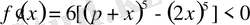шығады. Сондықтан белгілі теорема бойынша функциясы 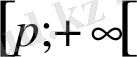сәулесінде кемиді, олай болса 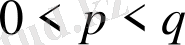шартынан 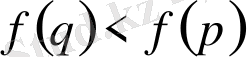теңсіздігі шығады, яғни 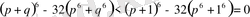бұл арадан .
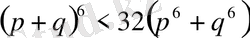Теорема 2. 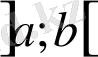интервалының әрбір нүктесінде 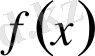функциясының туындысы болсын. Осы интервалдың шектеулі нүктелерінде туынды нөлге айналсын. Интервалдың қалған нүктелерінде туынды таңбасы оң болса, онда 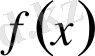функциясы 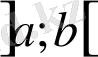интервалында өседі.
Теорема 3. 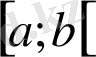интервалының әрбір нүктесінд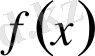е және 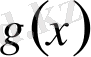функциялары үзіліссіз және әрбір нүктеде туындысы болсын. 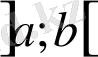интервалының барлық нүктелерінде 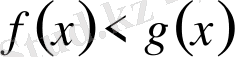(1) теңсіздігі орындалатын болса, онда осы интервалда 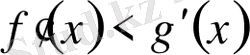(2) және 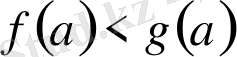орындалады.
Мысал 10.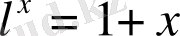; 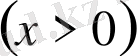теңсіздікті дәлелдеңдер. Туындысын табалық 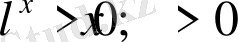. Бұдан теңсіздіктің дұрыстығын байқаймыз.
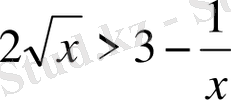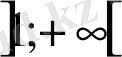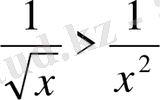
Мысал 11. теңсіздікті дәлелдеңдер, мұндағы үшінші теореманың екі шартының орындалатынын тексереміз. аралықта берілген теңсіздікті мүшелеп дифференциалдасақ, 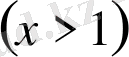шығады. 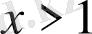болғанда теңсіздіктің дұрыстығы өзінен байқалады. Егер 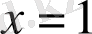десек, теңсіздік теңдікке айналады. Сонымен, теорема 3 бойынша теңсіздік орындалады.
Теорема 2′. 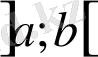интервалының әрбір нүктесінд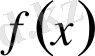е және 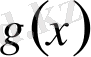функциясының туындысы болсын. 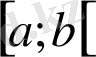жарты интервалында функцияоар үзіліссіз. 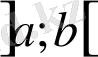интервалының бүкіл өн бойында 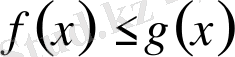(1) теңсіздік орындалу үшін бір мезгілде келесі шарттар орындалуы керек.
1. 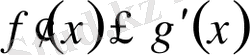(1′); 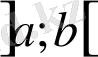интервалының бойындағы барлық 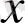-тер үшін орындалады;
2. Бұл үшін 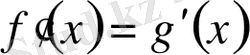(2′) теңдігі орындалатын 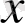нүктелер жиыны 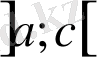түріндегі ешқандай интервалды толтырмайды. Мұндағы ;
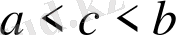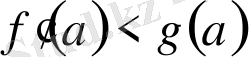3. (3′)
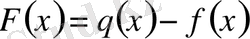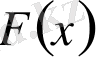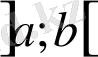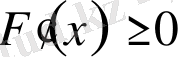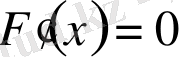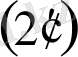
болсын. Онда ; интервалында үзіліссіз және осы интервалда : ; : 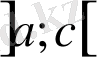; 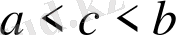ешбір интервалда толық қарастырмайтын жиында .
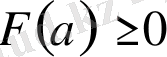
Ең алдымен 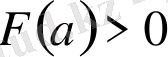жағдайды қарастыралық. Теорема 1 бойынша 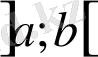интервалда 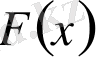кемімейді. Сондықтан 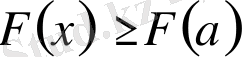; егер 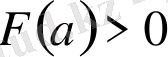болса, онда 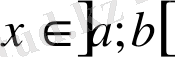үшін 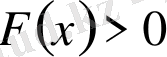,яғни 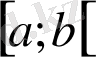интервалында .
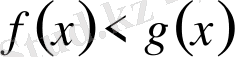Енді 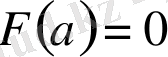жағдайды қарастыралық. 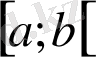сәулесінде 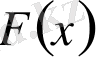функциясы кемитіндіктен 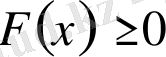. 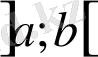интервалынан 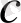санын белгілейік, (Яғни 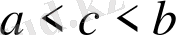). 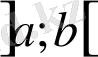интервалынан ең болмағанда 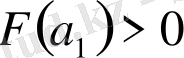болатындай бір нүкте табылатынын көрсетелік. Шынында да, керісінше жорысақ, 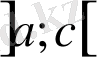интервалында 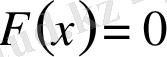деген қорытындыға келіп едік. Сонымен, 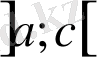интервалында 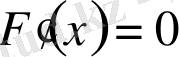, бұл (2′′) шартына қайшы. Демек, 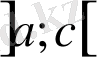интервалында 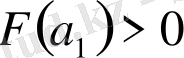болатындай 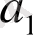нүкте болады. Сондай - ақ 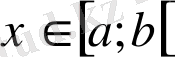және 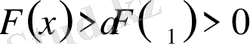, себебі 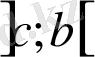аралығында 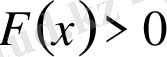. Бірақ біз 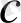нүктесін нүктесіне өте жақсы етіп алуымызға болады. Демек, 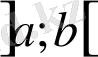интервалының барлық нүктесінде 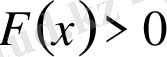, яғни, 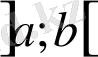-да .
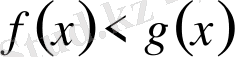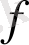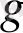Теорема 4. және функцияларының әрбірі 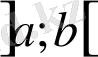жарты интервалында үзіліссіз және 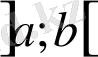интервалдың әр нүктесінде -ші дәрежелі туындысы болса, онда 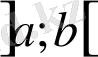интервалдың бойында 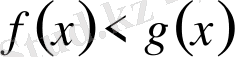(4) теңсіздігі орындалуы үшін мынадай шарттардың орындалуы жеткілікті.
1. 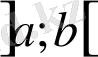интервалдың әр нүктесінде (4) теңсіздігінен -рет туынды алғанда шығатын 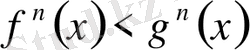(5) теңсіздігі берілген интервалда дұрыс болады.
2. Жарты интервалдың басында (яғни ) ең болмағанда ;
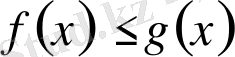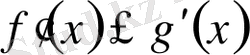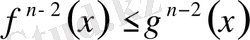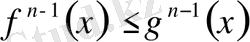,..., ; (6) тұжырымсыз теңсіздіктер орындалады.
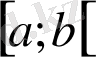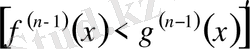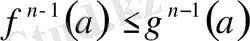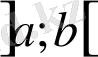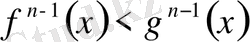Дәлелдеу. -да болғандықтан (5- теңсіздік) және шарты орындалатынын ескерсек , -да теңсіздігі орындалады.Демек, 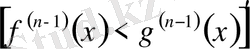шарты 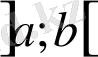интервалдың әр нүктесінде орындалады. Сонымен бірге (6) шарт бой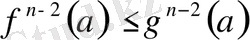ынша . Сондықтан теорема 3 бойынша 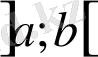-ның әр нүктесінде 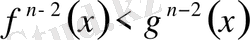шарты орындалады. Осыларға ұқсас тұжырымдар жасай отырып 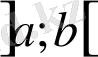-ның барлық нүктесінде қатаң теңсіздіктер орындалатындығына көз жеткізуге болады: 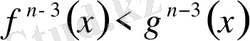;..., 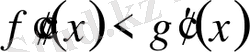; 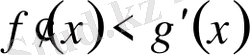және.
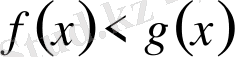Мысал 12. 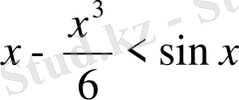(7) теңсіздікті дәлелде, мұндағы 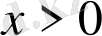. Берілген (7) теңсіздікті біртіңдеп дифференциалдасақ 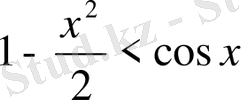, 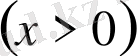(8) 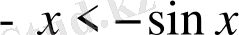, (9). Соңғы теңсіздік (яғни 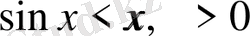) дұрыс орындалады. 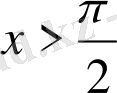болғанда .
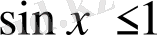Сонымен бірге (7), (8) - дегі қатаң теңсіздіктерді тұжырымсыз теңсіздіктермен ауыстыруға болады. Сонда 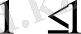шығады да (7), (8) ақиқат теңсіздікке айналады. Сондықтан теорема 4 бойынша 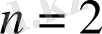болғанда (7) теңсіздк орындалады.
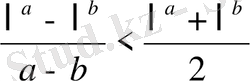
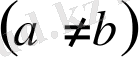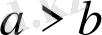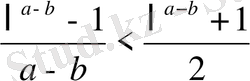
Мысал 13. (10) теңсіздікті дәлелдеңдер. (10) теңсіздіктегі a; b реті айтылғандықтан деп аламыз. (10) теңсіздікті 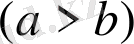түрінде жазамыз.
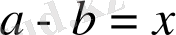десек, берілген теңсіздікті 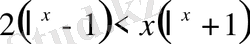, 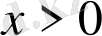(11) теңсіздікті екі рет дифференциалдасақ, 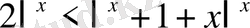, 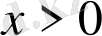(12).

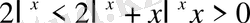
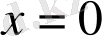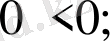
Соңғы теңсіздіктің ақиқаттығы бірден байқалады. Сонымен бірге (11), (12) теңсіздіктердегі таңбасын = ауыстырсақ, десек, 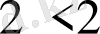сияқты ақиқат теңсіздік аламыз, теорема 4 бойынша (11), ал одан (10) теңсіздігі орындалады.
1.3 Екінші ретті туындынының көмегімен теңсіздіктерді дәлелдеу
Егер 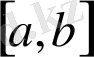кесіндісінде 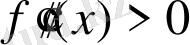болса, онда f функциясының графигі 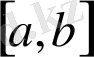аралығында хордадан жоғары жатқан 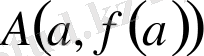және 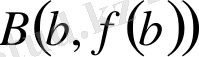,бірігу нүктелерінде болады. Хорда нүктелеріне сәйкес келетін ординатаны табамыз және 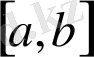кесіндісінен кез келген нүктесін таңдап аламыз. 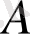және 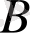нүктелері арқылы өтетін түзудің теңдеуі: y=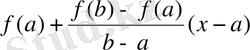. x=c болғанда yхорда=.
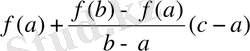Сондықтан y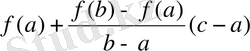= (13)
Егер 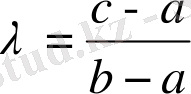болса, онда

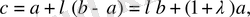
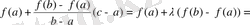
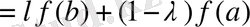
болады. Бұл (1) теңсіздігін қайта жазуға мүмкіндік береді.
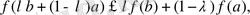мұндағы .
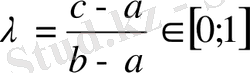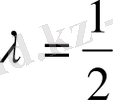болғанда, табатынымыз 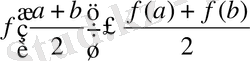. (14)
Сөйтіп, біз келесі теореманы дәлелдедік:
Теорема 5. Егер 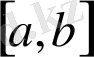кесіндісінде 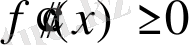теңсіздігі орындалса, онда кез келге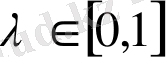н үшін 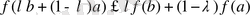теңсіздігі орындалады.
Егер 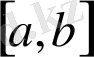аралығында 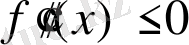, онда 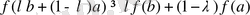теңсіздігі осы сияқты дәлелденеді.
Мысал 14. Теңсіздікті дәлелдендер:
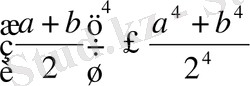. (15)
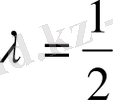Шешуі: , онда және болғанда, (14) және (15)-тен қорытып шығарамыз.
Мысал 15. Дәлелдеңдер: егер 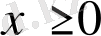болса,
Шешуі: 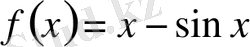; ; 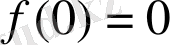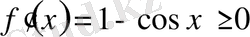, яғни 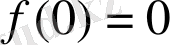, , 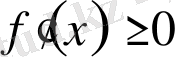ендеше .
Мысал 16. 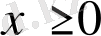, болғанда 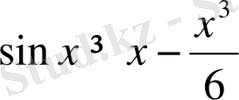екенін дәлелдейік.
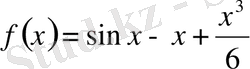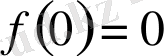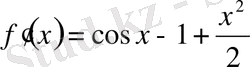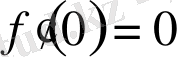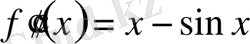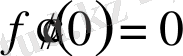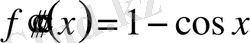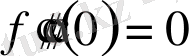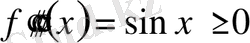,; , ; ; , , , . Енді кері жүріп және 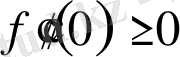өйткені 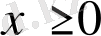болғанда 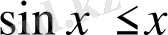екені жоғарыда дәлелдегенін ескеріп 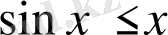екені жоғарыда дәлелденгенін ескеріп 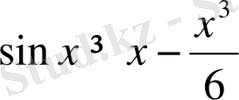деген қорытындыға келеміз, яғни теңсіздік дәлелденді.
Туындыны қолданып алгебраның көптеген есептерін шешуге болады, мысалы теңдеулер:;; ; .
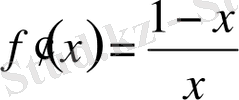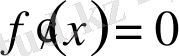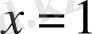Осы нүктеде функция өзінің максимум мәнін қабылдайды, 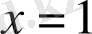мәнін теңдеуге қойсақ, ол теңдеудің түбірі екенін көреміз.
Мына 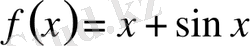функциясы периодты функция ма?
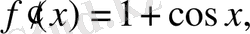
Шешуі: 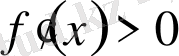яғни функция барлық аралығында өседі, әрі кризистік нүктелерінде үздіксіз, яғни функция периодты емес. Себебі периодты функция аргументтің бір мәніне сәйкес мәнін қайталай береді, ал мұнда аргументтің бір мәніне функцияның бір ғана мәні сәйкес келеді.
1.4 Туындының көмегімен Ньютон биномының формуласын есептеу

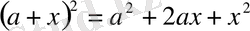
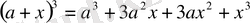
Бұл формулалар жеке жағдайының жалпы формулалары болады. 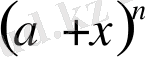өрнегінің жақшаларын ашсақ немесе өз өзіне n рет екімүшесін көбейтсек, 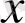-ке қатысты 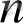дәрежелі көпмүшелік шығады. Оның коэффициенттерін білмегендіктен, жауабын мына түрде жазайық.
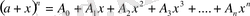(16)
Бізге 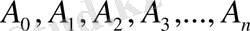коэффициентерінің өрнегін табу керек. 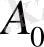табу үшін (16) теңдеуінің екі жағын да мәнінің орнына 0 қоямыз. Сонда
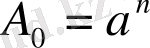(17)
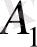-ді табу үшін (16) теңдеуінің екі жағын да дифференциалдап, 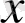-тің орнына 0-ді қоямыз. Дифференциалдау формуласынан мынаны аламыз:
.
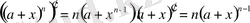Екінші жағынан
.
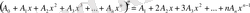Ендеше, 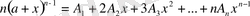(18)
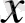-тің орнына 0-ді қойып, nan-1=A1 аламыз. Сөйтіп
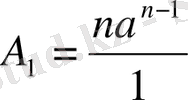(19)
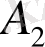- ны табу үшін (18) теңдеуінің екі жағын да дифференциалдап 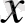-тің орнына 0-ді қоямыз. Табатынымыз:
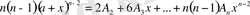, бұдан
.
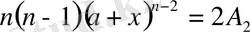Ендеше 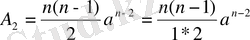(20)
Қалған коэффициенттерін осы тәсілмен табады. Егер (16) теңдеуін 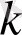рет дифференциалдасақ, онда алатынымыз:
Бұл теңдікте 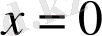деп алып, табатынымыз:

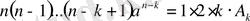
одан 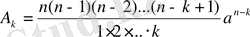(21)
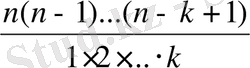сандарын биномиальдық коэффициенттер деп атаймыз және 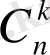деп белгілейміз. Осылайша, 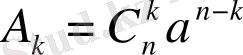, мұндағы
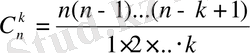(22)
Сондықтан
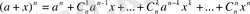(23)
(23) формуласын Ньютон биномы формуласы деп атаймыз. Теңдіктің оң жағы 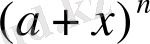биномының дәрежелік жіктелуі деп аталады.
Биномиальдық коэффициенттер формуласын басқа түрде жазуға болады, ол үшін көбейтінді үшін 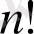(n-факториал) белгілеуін қолданып, (22) формуласындағы бөлшектің бөлімі мен алымын 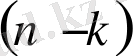- ға көбейтіп, алатынымыз:

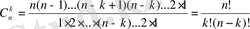
Сөйтіп,
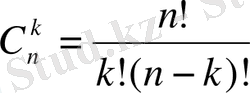(24)
Есіңде болсын, .
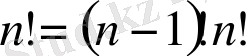(23) формуласында 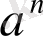- ның коэффициентті 1-ге тең. Сондықтан 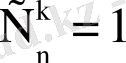деп есептейді. 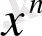-ның коэффициетті да 1-ге тең, болғандықтан 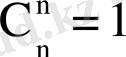деп есептейді. Бұл теңдіктер (24)формуласынан шығады, егер 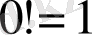шарттары орындалса.
Мысал 17. 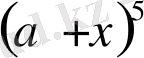биномының дәрежелік жіктелуін табамыз.
Шешуі: Біздің жағдайымызда 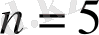. 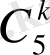биномиальдық коэффициенттерін есептейік: , , , ,
, .
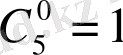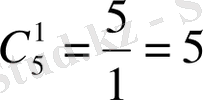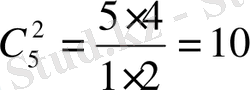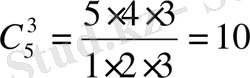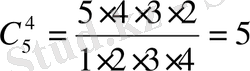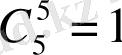Ендеше, (23) формуласынан табатынымыз:
.
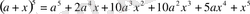Мысал 18. 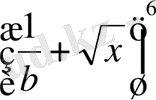биномының дәрежелік жіктелуін табайық.
Шешуі: Біздің жағдайымызда , -ның орнына , 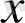-тің орнына 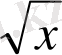қоямыз. Өйткені,
, , , ,
, , ,
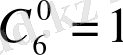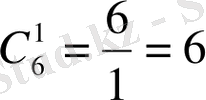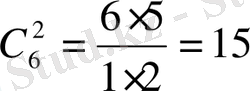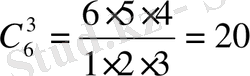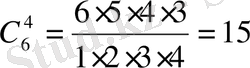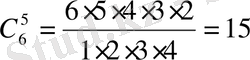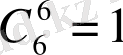Болса, онда
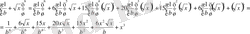болады.

1.5 Қиындығы жоғары теңсіздіктерді дәлелдеуге туындыны қолдану

Орта мектептің жоғары сынып оқушыларына арнап функцияның туындысы қолданылатын есептердің бірнеше түрін қарастыралық. Бұл есептердің кейбіреуі мектеп математикасындағы дәстүрлі есептерден өзгешілігі тек тұжырылымдалуында ғана болса, екіншілері өздерінің мәнді өзгешіліктерімен сипатталады.
Алдымен функцияларды зерттеуге арналған орта мектептің бағдарламасындағы дәстүрлі есептерге барынша мазмұндас есептер біріншіден оқушылардың туындыны қолдану аясын кеңейтеді, екіншіден есептерді бір тілден екінші тілге аудару арқылы шәкірттердің жан-жақты дамуына мүмкіндіктер туады. Ол есептер ең болмағанда басқа жағдайда, басқа терминде тұжырымдалып қолданбалы аспектіде математикалық дамудың маңызды көрсеткішіне айналады. Функционалдық теңсіздіктерді дәлелдеуге берілген барынша жай есептер жоғарыда аталған есептердің мысалы бола алады. Теңсіздіктің дұрыстығын туынды арқылы дәлелдеу белгілі бір аралықта дифференциалданатын функцияның монотонды болу шартына негізделген. Функцияның өспелі және кемімелі болуы келесі теоремалармен анықталады.
Теорема 1. Функцияның өспелі болуының жеткілікті шарты:
Егер 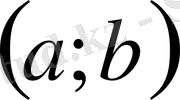аралығының әрбір нүктесінде 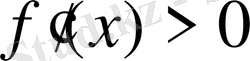теңсіздігі орындалса, онда функция осы аралықта өспелі болады.
Теорема 2. Функцияның кемімелі болуының жеткілікті шарты:
Егер 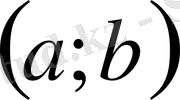аралығының әрбір нүктесінде 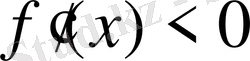теңсіздігі орындалса, онда функция осы аралықта кемімелі болады.
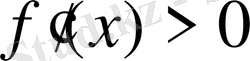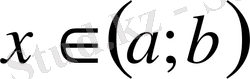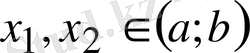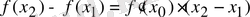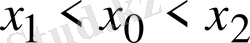Дәлелдеуі: 1) Айталық, , теңсіздігі орындалсын. Онда кез келген , нүктелері үшін , . Мұнда 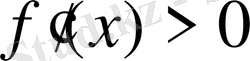, 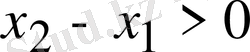болғандықтан, 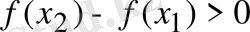немесе 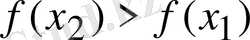теңсіздігі әрбір 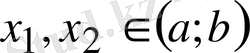, , нүктелері үшін орындалатынын көреміз. Яғни 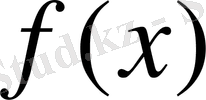функциясы 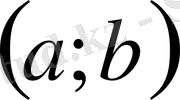аралығында өспелі болады.
2) тұжырым да осы сияқты дәлелденеді.
Теоремадағы және 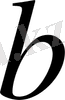сандарының орнына сәйкес 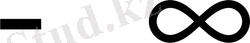және символдарын алуға болады. Бұл жағдайда да теорема орындалады. Сонымен қатар, жоғары математика курсында 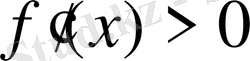, 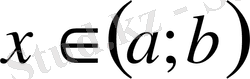(немесе 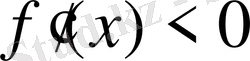) шарты функцияның 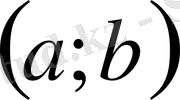аралығында өспелі және кемімелі болуы үшін қажетті және жеткілікті болатындығы жөніндегі сәйкес тұжырымдар дәлелденеді.
Осы қасиетті пайдаланып, 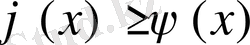түріндегі теңсіздіктің, мұндағы және функциялары анықталу облыстары бірдей дифференциалданатын функциялар дұрыстығын дәлелдеуге болады.
Дифференциалданатын функцияның монотондылық қасиетіне сүйеніп, жоғарыдағы теңсіздікті дәлелдеу үшін мынадай алгоритмді қолдануға болады:
1) функциясының анықталу облысын табамыз. Айталық функциясы аралығында анықталған болсын.
2) функциясын үздіксіздікке зерттеп, оның туындысын табамыз. Сонда болғанда және екені анықталса, онда функциясы өспелі болады да, сондықтан теңсіздігі орындалады.
3) функциясы аралығында монотонды болмай, және қандай да бір нүктесінде өзінің максимум немесе минимум мәндерінің бірін қабылдауы мүмкін. Бұл жағдайда болса, онда үшін теңсіздігі орындалады (мұнда теңсіздігінің шешімдері болмайды), ал егер болса, онда барлық тер үшін теңсіздігі орындалады (мұнда теңсіздігінің шешімдері болмайды).
функциясының 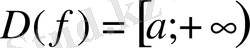аралығында бірнеше экстремум нүктелері болған жағдайда, көрсетілген аралықта функциясының тек бір ғана экстремум нүктелері болатын аралықтарға жіктеу керек.
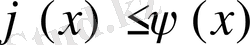болғанда теңсіздігінің орындалатындығы да осы сияқты дәлелденеді.
Енді біз үздіксіз функцияның монотондылық қасиетін пайдаланып, теңсіздіктің дұрыстығын дәлелдеуге мысалдар қарастырайық [82].
1-мысал. 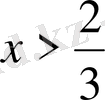болғанда 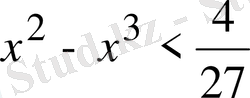теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 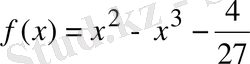функциясын 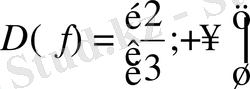аралығында қарастырайық. Бұл функция көрсетілген аралықта үздіксіз және дифференциалданатын функция.
Функцияның туындысын табайық: .
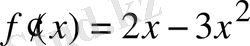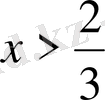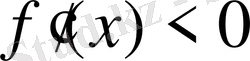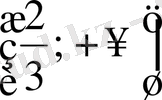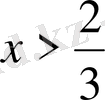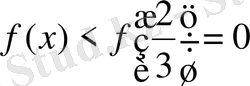
Сонда болғанда болғандықтан, функциясы аралығында кемімелі функция болады. Сондықтан болғанда 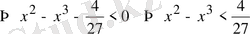теңсіздігі орындалады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
2-мысал. 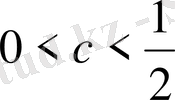болғанда 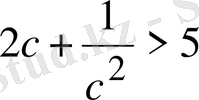(1) теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 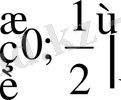аралығында 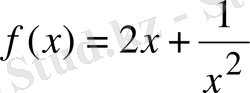функциясын қарастырайық. Бұл функцияның туындысы мынаған тең: .
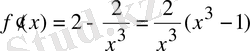Сонда 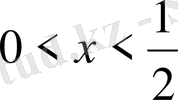болғанда 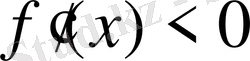орындалатындығы айқын. Олай болса, 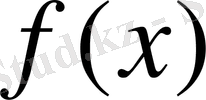функциясы 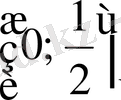аралығында кемімелі. Сондықтан 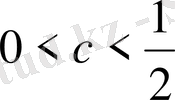болғанда 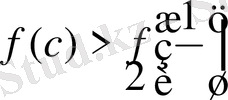болады. Бірақ .
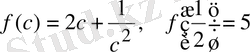Демек, (1) теңсіздік ақиқат.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
3-мысал. және болғанда теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 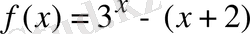функциясын 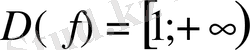аралығында қарастырайық. Бұл функция көрсетілген аралықта екі дифференциалданатын функцияның айырымы ретінде дифференциалданатын функция болады.
Функцияны монотондылыққа зерттейік. Ол үшін оның туындысын табамыз: .
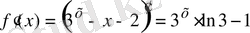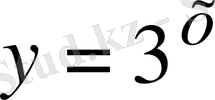функциясы 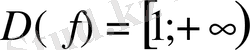аралығында өспелі, олай болса, .
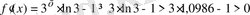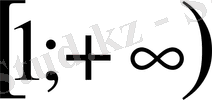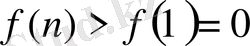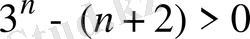
Демек, функциясы аралығында өспелі. Сондықтан болғанда, , яғни 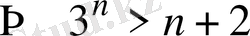теңсіздігі орындалады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
4-мысал. 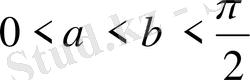болғанда 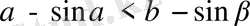теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 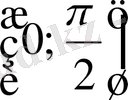аралығында анықталған көмекші 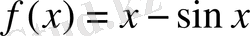функциясын қарастырайық. Бұл функция көрсетілген аралықта екі дифференциалданатын функцияның айырымы ретінде дифференциалданатын функция болады.
Оның туындысын табайық: .
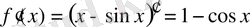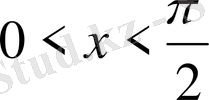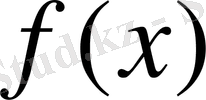Сонда болғанда, теңсіздігінің орындалатындығы ақиқат. Олай болса, функциясы аралығында өспелі функция, сондықтан 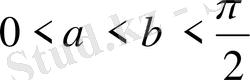болғанда, 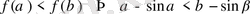теңсіздігі орындалады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
5-мысал. -ның барлық мүмкін мәндерінде 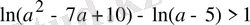теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 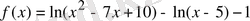функциясын қарастырамыз және оның анықталу облысын табамыз:

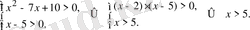
Бұл функция 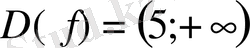аралығында дифференциалданатын функция және оның туындысы мынаған тең: .
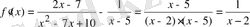Сонда болғанда, 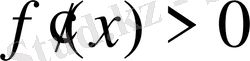болатындықтан, 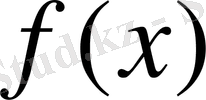функциясы 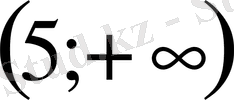аралығында өспелі функция.
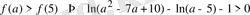
Сондықтан болғанда 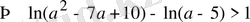теңсіздігі орындалады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.

6-мысал. болғанда, 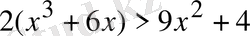теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 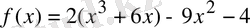функциясын қарастырамыз. Оның туындысын табамыз: .
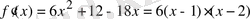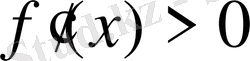Бұдан болғанда, теңсіздігі орындалатыны, яғни функциясының 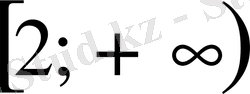аралығында өспелі функция болатындығы ақиқат.
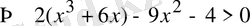
Сондықтан болғанда, , яғни 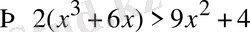теңсіздігінің орындалатындығы айқын.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
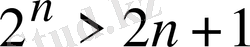7-мысал. Кез келген натурал болғанда теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: болғанда теңсіздіктің орындалатыны ақиқат. 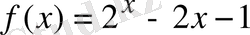функциясын 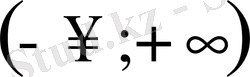аралығында қарастырайық. Оның туындысы 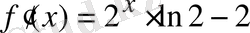, болғанда оң таңбалы, яғни функциясы монотонды өспелі. Бұдан дербес жағдайда, болғанда 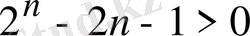, олай болса, болғанда 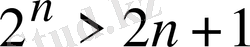теңсіздігінің орындалатындығы шығады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
8-мысал. 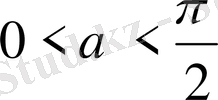болғанда, 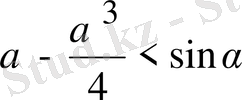теңсіздігінің орындалатындығын дәлелдеңдер.
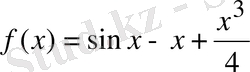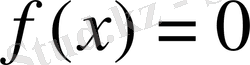Дәлелдеуі: функциясын аралығында қарастырамыз. болғанда, болады. Сонда біз, бұл функцияның көрсетілген аралықта монотонды өспелі екендігін, яғни 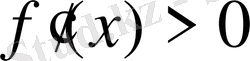теңсіздігі орындалатынын көрсете алсақ, онда берілген теңсіздіктің дұрыстығы ақиқат болады.
Функцияның туындысын табайық:
.
Сонда 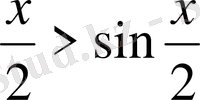болғандықтан, 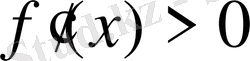болады. Олай болса, 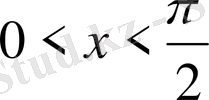болғанда 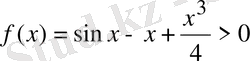теңсіздігінің, ал бұл 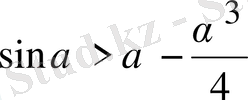теңсіздігінің дұрыс екенін көрсетеді.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
9-мысал. -тің барлық нақты мәндерінде 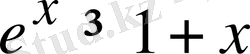теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: 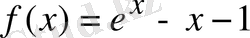функциясын қарастырамыз.
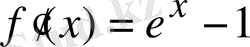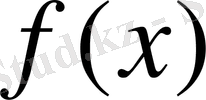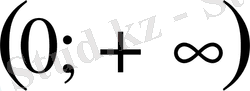
Оның туындысы -ге тең. болғанда, теріс таңбалы, ал болғанда, оң таңбалы және болғанда нөлге тең. Олай болса, функциясы аралығында кемімелі, ал аралығында өспелі. Сонда нүктесінде функцияның мәні нольге тең болғандықтан, оның барлық қалған мәндері оң таңбалы, яғни 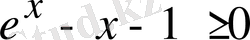болады. Бұдан 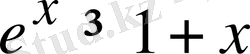теңсіздігінің орындалатыны ақиқат екені шығады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
10-мысал. болғанда, теңсіздігінің орындалатынын дәлелдеңдер.
Дәлелдеуі: функциясын аралығында қарастырайық. Бұл функцияның туындысы аралығында оң таңбалы, өйткені бұл аралықта , және . Олай болса, функциясы аралығында монотонды өспелі.
Сонда болғандықтан, болғанда, , яғни немесе теңсіздігінің орындалатыны ақиқат екені шығады.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
11-мысал. Теңсіздікті дәлелдеңдер: , .
Дәлелдеуі: Алатынымыз: . Айталық болсын. Сонда .
болатындығын дәлелдейік. болсын. болғанда . Туындыны табамыз: . Сонда болғанда, болады. Теңсіздіктің дұрыстығы дәлелденді. теңсіздігінің дұрыстығы да осы сияқты дәлелденеді.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
12-мысал. және , болғанда, теңсіздігінің орындалатынын дәлелдеңдер.
Дәлелдеуі: Теңсіздіктің екі жағында бірдей -не бөліп табатынымыз: немесе , мұндағы .
функциясын үшін қарастырайық. болғанда . ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.