Комплекс сандар: өріс пен амалдар, түрлері, Эйлер формуласы және түбірлер


4) Комплекс сандарға қолданылатын амалдар
5) Комплекс сандар өрісі
6) Эйлер тепе-теңдігі. Комплекс сандардың көрсеткіштік түрі. Мысал келтіру.
Начало формы
Қосымша А
Комплекс сандар
 комплекс сан деп
комплекс сан деп
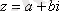 түріндегі өрнек айтылады (комплекс санның алгебралық түрі), мұндағы
түріндегі өрнек айтылады (комплекс санның алгебралық түрі), мұндағы
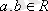 - нақты сандар,
- нақты сандар,
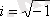 - жорамал бірлік.
- жорамал бірлік.
 және
және
 сандарын
сандарын
 комплекс санының сәйкес нақты ж7әне жорамал бөлігі деп атайды,
комплекс санының сәйкес нақты ж7әне жорамал бөлігі деп атайды,
 ,
,
 деп белгіленеді.
деп белгіленеді.
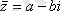 саны
саны
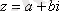 комплекс санына түйіндес деп аталады. Келесі өрнектер орынды
комплекс санына түйіндес деп аталады. Келесі өрнектер орынды
1)
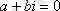

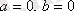 ;
;
2)
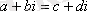

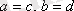 .
.
Алгебралық түрдегі комплекс сандарға қолданылатын амалдар
Екі комплекс сан берілген
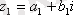 және
және
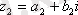 .
.
1.
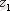 және
және
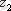 сандарының қосындысы (+) (айырымы (- ) ) деп
сандарының қосындысы (+) (айырымы (- ) ) деп
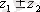
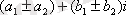 комплекс саны айтылады.
комплекс саны айтылады.
2.
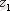 және
және
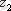 сандарының көбейтіндісі деп
сандарының көбейтіндісі деп
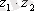
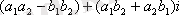 комплекс саны айтылады.
комплекс саны айтылады.
3.
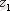 -дің
-дің
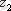 -ке бөліндісі деп (
-ке бөліндісі деп (
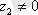 )
)
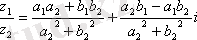 комплекс саны айтылады.
комплекс саны айтылады.
Сонымен, комплекс сандарының қосындысы, айырымы, бөліндісі
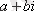 екі мүшені қосу, азайту ережесі бойынша есептелінеді, тек
екі мүшені қосу, азайту ережесі бойынша есептелінеді, тек
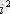 -ты -1-ге айырбастау керек. Бөлу де сол сияқты, бөлшекті бөлімнің түйіндесіне көбейту керек:
-ты -1-ге айырбастау керек. Бөлу де сол сияқты, бөлшекті бөлімнің түйіндесіне көбейту керек:
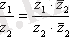 .
.
Комплекс санның геометриялық кескінделуі
Әрбір
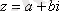 комплекс санына
комплекс санына
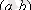 сандар жұбы бірмәнді сәйкес келеді, ал
сандар жұбы бірмәнді сәйкес келеді, ал
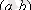 сандар жұбының геометриялық бейнесі ретінде жазықтықтағы нүктені немесе осы нүктенің радиус - векторын алуға болады, онда
сандар жұбының геометриялық бейнесі ретінде жазықтықтағы нүктені немесе осы нүктенің радиус - векторын алуға болады, онда
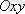 жазықтығында
жазықтығында
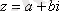 комплекс саны координаталары
комплекс саны координаталары
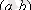 болатын
болатын
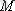 нүктесімен немесе осы нүктенің радиус - вектормен
нүктесімен немесе осы нүктенің радиус - вектормен
 бейнеленеді. (Сурет А. 1) .
бейнеленеді. (Сурет А. 1) .
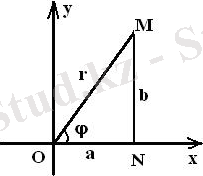
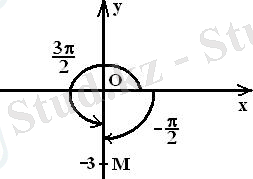
Сурет А. 1 Сурет А. 2
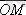 векторының ұзындығы деп комплекс санның модулі аталады және
векторының ұзындығы деп комплекс санның модулі аталады және
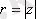 деп белгіленеді.
деп белгіленеді.
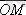 векторы мен
векторы мен
 осі арасындағы
осі арасындағы
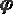 бұрышы комплекс санның аргументі деп аталады, белгіленуі
бұрышы комплекс санның аргументі деп аталады, белгіленуі
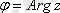 . Әрбір
. Әрбір
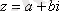 комплекс санға оның модулі бірмәнді сәйкес келеді:
комплекс санға оның модулі бірмәнді сәйкес келеді:
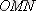 үшбұрышынан
үшбұрышынан
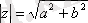 . Аргумент болса бірмәнді сәйкес келмейді,
. Аргумент болса бірмәнді сәйкес келмейді,
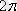 -ге еселі қосылғышқа дейін дәлдікпен анықталады:
-ге еселі қосылғышқа дейін дәлдікпен анықталады:
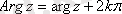 (
(
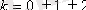 ), мұндағы
), мұндағы
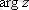
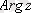 аргументтің негізгі мәні, ол
аргументтің негізгі мәні, ол
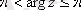 (немесе
(немесе
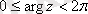 ) шартын қанағаттандырады. Аргументтің негізгі мәнін келесі формулалардан табады:
) шартын қанағаттандырады. Аргументтің негізгі мәнін келесі формулалардан табады:

Егер комплекс сан координата осьтерінде жатса, онда модуль мен аргументті оның геометриялық бейнесі бойынша табуға болады.
Мысал А. 1
-
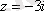 санының бейнесі бойынша (А. 2 суреттегі
санының бейнесі бойынша (А. 2 суреттегі
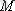 нүктесі) координат басынан ұзындығы 3 бірлікте орналасқандықтан, оның модулі
нүктесі) координат басынан ұзындығы 3 бірлікте орналасқандықтан, оның модулі
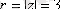 .
.
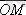 векторымен және
векторымен және
 осімен құралған
осімен құралған
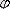 бұрышы
бұрышы
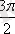 -ге (немесе
-ге (немесе
 ) тең, сондықтан аргументтің негізгі мәні
) тең, сондықтан аргументтің негізгі мәні
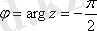 немесе
немесе
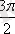 .
.
Комплекс саннның екі түрі болады: тригонометриялық, көрсеткіштік. Тригонометриялық түрін А. 1 суретіндегі
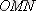 үшбұрышынан табуға болады
үшбұрышынан табуға болады
 және
және
 -ны
-ны
 және
және
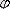 арқылы өрнектейміз:
арқылы өрнектейміз:
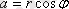 ,
,
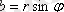 . Сонда
. Сонда
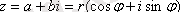 - тригонометриялық түрі. Эйлер формуласын қолданып
- тригонометриялық түрі. Эйлер формуласын қолданып
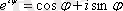 , тригонометриялық түрден көрсеткіштік түрді алуға болады:
, тригонометриялық түрден көрсеткіштік түрді алуға болады:
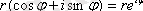 .
.
Мысал А. 2
-Комплекс саннның тригонометриялық түрін, көрсеткіштік түрін табайық
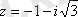 .
.
 ,
,
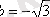 , сондықтан модулі
, сондықтан модулі
 . Комплекс сан үшінші квадрантада орналасқандықтан, аргументті келесі формуламен есептейміз
. Комплекс сан үшінші квадрантада орналасқандықтан, аргументті келесі формуламен есептейміз
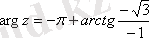 =
=
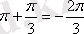 . Сонымен,
. Сонымен,
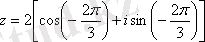 -комплекс саннның тригонометриялық түрі,
-комплекс саннның тригонометриялық түрі,
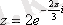 - көрсеткіштік түрі.
- көрсеткіштік түрі.
Тригонометриялық түрдегі комплекс сандарға қолданылатын амалдар
Екі комплекс сан тригонометриялық түрде берілген болсын
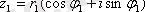 және
және
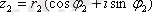 , сонда
, сонда
а)
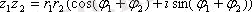 ;
;
б)
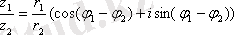 .
.
Сонымен, комплекс сандарды көбейткенде, олардың модульдері көбейтіледі, ал аргументтері қосылады; бөлгенде - модульдері бөлінеді, аргументтері азайтылады.
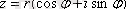 комплекс санды
комплекс санды
 - ші дәрежеге шығару үшін, бұл санға
- ші дәрежеге шығару үшін, бұл санға
 рет көбейту ережесін қолдану керек. Сонда Муавр формуласын аламыз:
рет көбейту ережесін қолдану керек. Сонда Муавр формуласын аламыз:
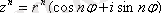 . Айта кетелік, Муавр формуласы
. Айта кетелік, Муавр формуласы
 -нің кез келген нақты мәнінде орындалады: бүтін, бөлшек, оң, теріс.
-нің кез келген нақты мәнінде орындалады: бүтін, бөлшек, оң, теріс.
Жорамал бірліктің дәрежесін есептеу формуласын білген жөн.
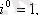
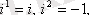
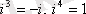 болғандықтан
болғандықтан
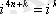 формуласы орынды, мұндағы
формуласы орынды, мұндағы
 тек төрт мәнді қабылдайды: 0, 1, 2, 3.
тек төрт мәнді қабылдайды: 0, 1, 2, 3.
Мысал А. 3
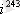 =
=
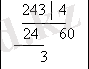 =
=
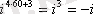 .
.
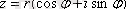 комплекс саннның
комплекс саннның
 -ші дәрелі түбірі
-ші дәрелі түбірі
 әртүрлі мән қабылдайды және
әртүрлі мән қабылдайды және
 =
=
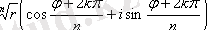 формуласымен есептелінеді, мұндағы
формуласымен есептелінеді, мұндағы
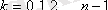 . Әрі қарай
. Әрі қарай
 -ның қалған мәндерінде түбірдің мәндері қайталанады. Бұл формуланы бөлшек көрсеткішті Муавр формуласынан алуға болады.
-ның қалған мәндерінде түбірдің мәндері қайталанады. Бұл формуланы бөлшек көрсеткішті Муавр формуласынан алуға болады.
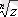 түбірін бейнелейтін нүктелердің геометриялық кескінделуіне келсек, центрі координата басында, радиусы
түбірін бейнелейтін нүктелердің геометриялық кескінделуіне келсек, центрі координата басында, радиусы
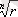 -ге тең шеңберді
-ге тең шеңберді
 бірдей бөлікке бөледі.
бірдей бөлікке бөледі.
 нақты санының
нақты санының
 - ші дәрежелі түбірінің де
- ші дәрежелі түбірінің де
 әртүрлі мәндері болады, олардың арасында бір, екі нақты түбірі болуы мүмкін немесе ешқандай түбірі болмауы мүмкін, ол
әртүрлі мәндері болады, олардың арасында бір, екі нақты түбірі болуы мүмкін немесе ешқандай түбірі болмауы мүмкін, ол
 -ның жұп, тақтығына және
-ның жұп, тақтығына және
 -тің таңбасына байланысты.
-тің таңбасына байланысты.
Мысал А. 4
- Келесі түбірдің барлық мәндерін табайық
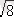 . Алдымен
. Алдымен
 =8 санын тригонометриялық түрге келтіреміз:
=8 санын тригонометриялық түрге келтіреміз:
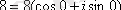 . Олай болса,
. Олай болса,
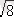 =
=
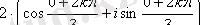 , мұндағы
, мұндағы
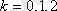 . Түбірдің мәндері:
. Түбірдің мәндері:
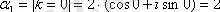 ;
;
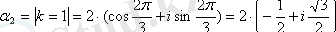 ;
;
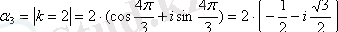 .
.
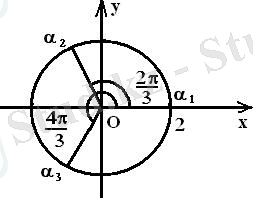
А. 3 суретінде
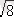 мәндері бейнеленген.
мәндері бейнеленген.
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz