Интегралдаудың негізгі әдістері және қолданылуы


Абай атындағы Қазақ Ұлттық педагогикалық университеті
Математика, физика және информатика институты
Математикалық анализ кафедрасы

РЕФЕРАТ
Тақырып: Интегралдаудың әдістері
Орындаған; Қальяхмет Назира
Тексерді: Шияпов Кадржан
Алматы 2021
Анықталған интеграл ертеректе жазық фигуралардың ауданын табу негізінде туындады. Ал қазір анықталған интеграл барлық техникалық ғылымдардағы аз шаманың үлкен сандарының қосындысын табуға арналған есептерді шешеуде қолданылады. Анықталмаған интеграл инетеграл (лат. integer-бүтін) -математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан-туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүкетенің жылдамдығы бойынша табу), екінші жағынан-аудан, көлем және доға ұзынығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып саналады. Интеграл сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама. Біз бұл курстық жұмыста білімнің әр түрлі саласына жататын, бірақ екеуінің де шешуін табу бір математикалқ аппаратқа негізделген екі есепті қарастырмақшымыз. Сөз болып отырған математикалық аппарат бірінші қарағанда функцияларды дифференциалдау мен интегралдау мәселесіне тура қатысы жоқ сияқты болып көрінеді. Тарихта да ұзақ уақыттар бойы бұл аппарат дифференциялдау байланыссыз өсіп дамыған. XVII ғасырдың аяғында-ақ бұл циклдегі есептеді шешудің ең күшті жңне ең жалпы әдісін оларды интегралдық есептеуде шешілетін мәселелермен байланыстыру жолында ғана жасауға болатыны анық болды. Біздің қарастырмақ болып отырған есептеріміздің бірі жазық фигуралардың ауданын есептеп шығару. Элементаралық геометрияда тек түзу сызықты кесінділер және шеңбер доғаларымен шенелген жазық фигуралардың аудандарын есептеп шығару әдісі беріледі. Кез-келген қисық сызықпен шенелген жазық фигураныңда ауданын табу жөніндегі жалпы геометриялық мәселені тек математикалық анализдің құралдарының жәрдемімен ғана шешуге болады. Кез келген жазық фигураның ауданын есептей білудің теориялық және ешқандай арнайы ыспаттаудың керек етпейді.

Тікелей интегралдау әдісі
Берілген интегралдардың астындағы функцияға қарапайым түрлендірулер және анықталмаған интегралдардың қасиетіне сүйеніп таблицалық интегралға келтіру арқылы интегралдау әдісін тікелей интегралдау деп атайды. Берілген интегралды таблицалық интегралға келтіруі үшін дифференциалды келесі түрде түрлендіру жиі қолданылады («интеграл астына енгізу» операциясы) :
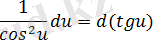
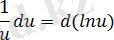
du=d(u+a), a-const
du
=
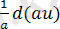 ,
a
,
a
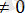
cosudu=d(sinu) sinudu=-d(cosu)
Жалпы алғанда,
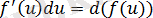 формуладан интегралдарды есептегенде жиі қолданылады.
формуладан интегралдарды есептегенде жиі қолданылады.
Айнымалыны ауыстыру әдісін қолданып интегралдау
Айнымалы ауыстыру әдісі интегралдау айнымалысының орнына жаңа айнымалыны енгізу арқылы кестелік интегралдарға келтіруге болады. Айнымалыны ауыстырудың жалпы әдісі жоқ.
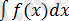 интегралын есептеу керек болсын.
интегралын есептеу керек болсын.
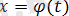 ауыстыруын қолданайық, мұндағы
ауыстыруын қолданайық, мұндағы
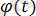 -үзіліссіз туындылары бар функция болсын.
-үзіліссіз туындылары бар функция болсын.
Сонда
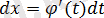 және анықталмаған интегралды интегралдау формулаларының инварианттылығы қасиетінің негізінде айнымалы ауыстыру формуласын аламыз:
және анықталмаған интегралды интегралдау формулаларының инварианттылығы қасиетінің негізінде айнымалы ауыстыру формуласын аламыз:
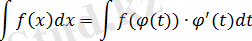
Бөліктеп интегралдау әдісі
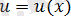 және
және
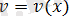 -үзіліссіз туындылары бар функциялар болсын. Онда
d
(
uv
) =
udv
+
vdu
. Осы теңдікті интегралдап
-үзіліссіз туындылары бар функциялар болсын. Онда
d
(
uv
) =
udv
+
vdu
. Осы теңдікті интегралдап
немесе
Бөліктеп интегралдау формуласын қолдану үшін интеграл астындағы өрнекті
 және
және
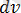 көбейткіштің көбейтіндісін жазу керек;
көбейткіштің көбейтіндісін жазу керек;
 және
және
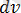 тапқаннан кейін бөліктеп интегралдау формуласы қолданылады. Бөліктеп интегралдау формуласын бірнеше рет қолдануға болады. Бөліктеп интегралдау арқылы табылатын интегралдардың кейбір түрлерін көрсетейік:
тапқаннан кейін бөліктеп интегралдау формуласы қолданылады. Бөліктеп интегралдау формуласын бірнеше рет қолдануға болады. Бөліктеп интегралдау арқылы табылатын интегралдардың кейбір түрлерін көрсетейік:
1.
(2. 10) -түріндегі интегралдар, мұндағы
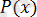 - көпмүше,
- көпмүше,
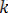 сан. Бұл интегралдарда
сан. Бұл интегралдарда
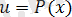 aрқылы белгілеп, ал басқа көбейткіштер
aрқылы белгілеп, ал басқа көбейткіштер
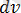 арқылы белгіленеді.
арқылы белгіленеді.
2.
(2. 12) -деп, ал қалған көбейткіштерді
 арқылы белгіленеді.
арқылы белгіленеді.
3.
мұндағы
 және
және
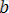 сандар.
сандар.
 деп
деп
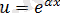 функциясын аламыз.
функциясын аламыз.
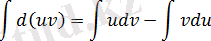
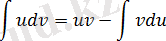
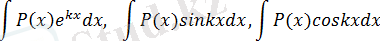
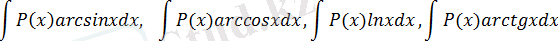
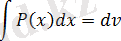
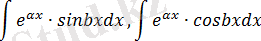
Анықталмаған интеграл
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz