Полярлық координаталарда анықталған интеграл арқылы жазық фигураның ауданын есептеу: формула, дәлелдеме және мысалдар (лемниската, кардиоида)


Анықталған интеграл бойынша жазық фигураның ауданы, қисық сызықтың ұзындығы, дене көлемі мен беті, , инерция моменті, берілген күштердің атқарған жұмыстары, және . жаратылыстану, техника есептеріде шығарылады. Интеграл бізде көпайнымалысы бар функцияларға да қолданыла береді.
Интегралдың тарихи квадратураларды табу есептерімен аса жақын байланысқан. Қандайда болмасын жазық фигуралардың квадратурасы жөніндегі есептер деп Ежелгі Греция мен Рим ғалымдары қазіргі біздің ауданды есептеуге берілген есептерді алған. Латынша "guadratura" дегеніміз квадрат пішінге келтіру деп аударылады. Ал осындай арнаулы терминдердің қажеттігі өзімізге қазір үйреншікті нақты сандар жайлы ұғымның сонау көне заманда(кейініректе XVIII ғасырға дейін) жеткілікті дамытылғанмен түсіндіріледі. Сондықтан аудандарды табуға берілген есептерді былайша тұжырымдауға тура келеді, мысалы: «Берілген дөңгелекпен тең шамалас квадратты салу керек». Мұнда «дөңгелектің квадратурасы туралы» құнды есеп циркуль мен сызғыштың көмегімен шығарылмайтыны белгілі.
Интеграл символын Лейбниц (1675жылы) енгізген. Бұлбелгі латын әріпінің
("summa" сөзінің 1ші әріпі) өзгертілген түрі. Интеграл сөзінің өзінЯ. Бернулли (1690жылы) ойлап тапқан. Соған қарағанда оның шығутегі латынша integroс өзіне сыятын болғандықтан, оның мәні: бұрыңғы қалыпқа түсіру, орнына келтіру. Интеграл сөзінің шығутегі басқаша болуыда мүмкін: "integer" дегеніміз бүтін деген мағынаны береді. И. Бернулли мен Г. Лейбниц хат-хабар алыса жүріп, Я. Бернуллидің ұсынысымен келіскен болатын. Сол 1696 жылы математиканың жаңа тармағының атауы интегралдық есептеу (calculusintegralis) пайдаболды, мұныИ. Бернуллиенгізді.
Полярлық координаталарымен берілген қисықты қарастырамыз. Қисық және полярлық бұрышы
теңдеулерімен берілген фигураның ауданын табалық.
Анықтама . ρ=ρ(φ) функциясы [φ 1 , φ 2 ] аралығында үзіліссіз, әрі теріс болмасын. Полярлық осьпен жасайтын бұрыштары φ 1 және φ 2 болатын екі полярлық радиустар және ρ(φ) қисығымен шенелген фигура қисық сызықты сектор деп аталады.
бұрышын n бөлікке бөлеміз.
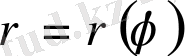
 2
2
ϕ 1
Анықтама. Полярлық радиустармен және қисығымен қоршалған фигураның ауданы деп ең үлкен ∆ϕ i →0 -дағы дөңгелек сызықты секторлардың аудандарының қосындысын айтады:
. (*)
Бұл дөңгелек сектордың ауданын анықтайық:
.
(*) қосындысы интегралдық, өйткені ол төменнен және жоғарыдан Дарбу қосындысымен шенелген, сондықтан оның шегі болғанда бар, яғни
.
Сонымен, фигураның ауданы мына формуламен табылады:
Есеп 1. лемниската қисығымен шектелген ауданды табатын болсақ.
Шешімі: Қисықтың симметриялылығын ескере отырып, берілген аудан ширегін есептеп, алынған нәтижені 4есе еселетеміз:
Шешуі:
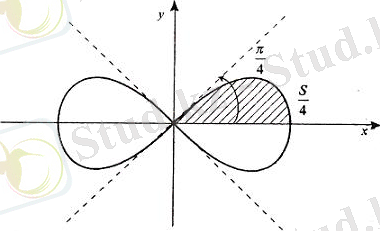
Полярлық координаталар жүйесінде r = f (φ) қисығы доғасымен және екі полярлық радиусы φ 1 = α және φ 2 =β шекарасы орналасқан фигураның ауданы интегралмен өрнектеледі.
Қисықтың симметриясына байланысты алдымен қалаған аумақтың төрттен бірін анықтаймыз
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz