Декарт координатындағы ауданды есептеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Декарт координатындағы ауданды есептеу.

[a, b] сегментінде үздіксіз y=f(x) функциясы оң болса, онда қисық сызықты трапецияның ауданы

\[S=\underline{{{\S}}}_{a}^{\ b}f(x)d x=\underline{{{\S}}}_{a}^{\ b}f d x\]

(1) формуласымен табылады. Енді [a, b] сегментінде f(x) <0 болсын. (1) формула бойынша

\[S=\ _{a}^{b}\;\left[f(x)\right]\!\!/x=-\stackrel{b}{\bigcup_{a}}\int\!\!(x)d x\]

(2) болады. (1) және (2) формуланы біріктіріп былай жазуға болады.

\[S=\bigcup_{a}^{b}\left\|f(x)d x\right.\]

(3) .

Қисық сызықты трапецияны шектеген қисық параметрлік теңдеумен берілген жағдайдағы ауданды есептейік. 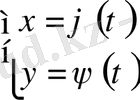(4) . Мұндағы

\[a\ \pounds\ \hat{x}\ =\left.\right.\hat{x}^{1}4!\hat{\mathrm{a}}j\ \big(a\ \big)=\hat{a},\ \left(\beta\ \right)=\hat{a}\]

болсын. Онда аудан

\[S=\underline{{{\S}}}_{a}^{\ b}f(x)d x=\underline{{{\S}}}_{a}^{\ b}f d x\]

формуласымен табылады. Бұл интегралдағы айнымалыны ауыстырайық.

\[x=j~(t~)~\mathrm{d}x=\phi^{'}(t~)d\]

(4) формула бойынша

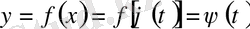болады. Сондықтан

\[S={\frac{\beta}{a}}{\int(t\oint^{\prime}(t)d t}\]

Полярлық координатасымен берілген қисықпен шектелген фигураның ауданын есептеу.

\[r=f(\theta)\]

доғасының қисығымен және сол доғаның шеткі нүктелерінің радиус векторларымен шектелген қисық сызықты сектордың ауданын есептеу керек болсын.

\[S={\frac{1}{2}}\int\!\![f(q)]J d\theta\]

Дененің көлемін белгілі көлденең қимасы бойынша есептеу.

Бір денені қарастырайық. Оның Ох осіне перпендикуляр жазықпен қиғандағы қималардың аудандары белгілі болсын дейік. Бұл қималарды көлденең қималар деп атаймыз. Сонда

\[V=bigcup_{a}^{b}{\hat{S}}(x)d x\]

Айналу денесінің көлемі. [a, b] сегментінде анықталған y=f(x) қисығы берілсін. аАВв қисық сызықты трапецияның Ох осінен айналуынан шыққан дененің көлемін есептеу керек болсын. Көлденең қималары радиусы айналу қисығының ординатасы у-тің абсолют шамасына тең дөңгелектер болады. Сондықтан қиманың ауданы

\[S(x){=}p y^{2}=\pi\left[f(x)\right]\]

болады. Сонда айналу денесінің көлемі

\[V=p\begin{array}{l}{{b}}\end{array}\!\iint_{a d}(x)\!\!\!\int_{a d}^{b}\!\!\!d x=\pi\sum_{a}^{b}y^{2}d x\]

болады.

4. Қисықтың доғасының ұзындығы және доғаның дифференциалы.

[a, b] сегментінде анықталған f(x) функциясы берілсін және y=f(x) қисығы үздіксіз болсын. Осы қисықтың А және В нүктесіне дейінгі доғасының ұзындығы мына формуламен есептеледі:

\[L=\bigcup_{a}{\iiint\!\!\!\!J}\quad\]

Қисық параметрлік теңдеумен берілген жағдайдағы доғаның ұзындығын есептейік. 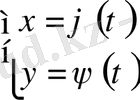. Мұндағы

\[a~\Xi~t~\leq b~~\alpha^{V_{A}\underline{{{k}}}}j~(t~)v\left(t~\right)\]

- үздіксіз туындылары бар үздіксіз функциялар болсын және

\[\phi^{\prime}(t)\]

берілген аралықта нөлге тең болмайтын болсын. Онда

\[L=bigcup_{a}^{\beta}\iiint{\overline{{\phi^{\prime}(t)+\psi^{\prime}{}^{2}(t)}}}\,d t\]

Енді қисықтың теңдеуі полярлық координаталарымен берілгендегі доғаның ұзындығының формуласын берейік.

\[r=f(\theta)\]

қисықтың теңдеуі берілсін, мұндағы

\[\hat{J}\]

-полярлық радиус,

\[\hat{O}\]

-полярлық бұрыш. Сонда

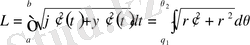5. Айналу денесінің бетінің ауданы.

y=f(x) қисығының Ох осінен айналуынан шыққан бет берілсін.

\[{\hat{a}}\models{\hat{\sigma}}\subseteq{\hat{a}}\]

аралығындағы сол беттің ауданының формуласы:

\[S=2\pi\frac{b}{a}\triangleright\sqrt{1+y^{\prime^{2}}}d x\]

Егер қисық параметр түрде берілсе,

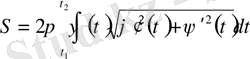\[{\begin{array}{l}{{\frac{1}{2}}x=j\,\left(t\right)}\\ {\mathbf{\hat{I}}}\end{array}}\left(\psi\left(\mathbf{\hat{\Pi}}\right)\geq0\right)\]

онда осы қисықтың Ох осінен айналуынан шыққан беттің ауданы төмендегідей формуламен есептеледі:

6. Меншіксіз интегралдар.

Анықталған интегралда интегралдау интервалдары шекті деп және интеграл астындағы функция сол аралықта шексіздікке айналмайды деп алдық. Ондай интегралдарды меншікті интегралдар деп атаймыз. Егер ең болмағанда жоғарыдағы екі шарттың біреуі орындалмаса, онда интеграл меншіксіз интеграл деп аталады.