Биологиядан есептер шығару

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Қазақстан Республикасының білім жӘне ғылым министрлігі
М.Х. Дулати атындағы Тараз өңірлік университеті

Ұстаз институты

Химия және биология __________кафедрасы

КУРСТЫҚ Жұмыс

Биологияны оқыту әдістемесі_________________________ ____пәні бойынша

Тақырыбы: Биологиядан есептер шығару әдістемесі

___________________________________ ________________________________

___________________________________ __________________________________

___________________________________ __________________________________

Білімгер Гурбанова Гулнур Тобы___ХБ-19-5 _____________
аты-жөні қолы
Жетекші : аға оқытушы ___Абжапарова А.С.
қызметі аты-жөні
Қорғауға жіберілді ____________________20____ж. __ _____________________
қолы

Жұмыс қорғалды __________________20__ж. бағасы ____________________
жазбаша
Комиссия мүшелері: _________________________ _____ ______________________
аты-жөні қолы

______________________________ ___ ___________________
аты-жөні қолы

Тараз 2021

МАЗМҰНЫ

КІРІСПЕ
3
1
Биологиядан есептер шығару
4
1.1
Биологиядан есептерді шығару әдістемесі. 9-сынып
8
1.2
Биологиядан шығармашылық тапсырмалар және оларды шешу әдістері
10

2.1
Тәжірибелік бөлім
Жалпы биологиядан есептерді шығару әдістемесі
16

ҚОРЫТЫНДЫ
21

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ.
22

Кіріспе

Мектеп пәндерін оқытуда қолданылатын оқыту әдістерінің бірі ретінде есептер шығару оқу материалын тереңірек және толық меңгеруге, алған білімдерін практикада қолдана білу қабілетін қалыптастыруға ықпал етеді. Сонымен қатар, шешуі үшін бірқатар сабақтас пәндер бойынша білім қажет болатын міндеттер ерекше рөл атқарады - оларды шешу үшін әртүрлі пәндерді оқуда алынған білімді жалпылау қажет, бұл қоршаған дүниенің заттары мен құбылыстары арасындағы терең байланыстарды анықтау. Жаратылыстанудың, техниканың және механиканың, биологияның, медицинаның және ғылыми білімнің басқа салаларының көптеген мәселелері процестерді формула түрінде математикалық модельдеуге дейін төмендетіледі, т.б. функционалдық тәуелділік түрінде. Мысалы, радиотехникадағы өтпелі процестер, химиялық реакциялардың кинетикасы, биологиялық популяциялардың динамикасы, ғарыш объектілерінің қозғалысы, экономикалық даму модельдері дифференциалдық теңдеулер көмегімен зерттеледі.
Курстық жұмыстың өзектілігі: Мектепте биология курсында ботаника, зоология, адам анатомиясы, адам және жануарлар физиологиясы, биохимия, генетика, молекулалық биология бағытындағы есептерді шығару.
Жұмыстың мақсаты: биологиялық есептерін шешу үшін дифференциалдық теңдеулерді, формулаларды қолдану мүмкіндігін қарастыру, пропорция құру арқылы пайызын анықтау.
Жұмыстың міндеттері: математикалық құбылыстарды функционалдық, салыстырмалы және қарама-қарсы зерттеу принциптеріне негізделген.
Зерттеу нысаны: биологиядан есептер шығаруда математикалық өрнектер - формулалар, функциялар, қолдану
Зерттеу әдісі: Математикалық модельдер - зерттелетін объектінің, құбылыстың, процестің белгілі бір қасиеттерін сипаттайтын математикалық өрнектер - формулалар, функциялар, теңдеулер және т.б. Математикалық модельді құру кезінде модельдеу объектісін эксперименттік зерттеу,
Жұмыстың практикалық маңызы: Биологиядан тапсырмалар және оларды шешуде оқу материалын тереңірек және толық меңгеруге, алған білімдерін практикада қолдану

1 Биологиядан есептер шығару

Тірі организм тым күрделі жүйе болып табылады, ол бірден барлық бөлшектерімен қарастырылады; сондықтан зерттеуші әрқашан белгілі бір мәселені шешуге қолайлы жеңілдетілген көзқарасты таңдайды. Бұл нақты биожүйелерді әдейі жеңілдету модельдеу әдісінің негізінде жатыр.
Әдетте, биологияда қолданылатын модельдер үш санатқа бөлінеді:
Жалпы заңдылықтар, патологиялық процестер, әртүрлі препараттардың әрекеті және т.б. зерттелетін биологиялық объектілік модельдер.Бұл модельдер класына, мысалы, зертханалық жануарлар, оқшауланған мүшелер жатады. Жасуша дақылдары, органелла суспензиялары және т.б. Физикалық (аналогтық) модельдер, яғни модельденетін нысанға ұқсас мінез-құлқы бар физикалық модельдер. Мысалы, әртүрлі жүктемелер кезінде сүйекте пайда болатын деформацияларды арнайы дайындалған сүйек үлгісінде зерттеуге болады. Қанның үлкен тамырлар арқылы қозғалысы резисторлар, конденсаторлар және индуктивті катушкалар тізбегі арқылы модельденеді[1].
Математикалық модельдер - зерттелетін объектінің, құбылыстың, процестің белгілі бір қасиеттерін сипаттайтын математикалық өрнектер - формулалар, функциялар, теңдеулер және т.б. Математикалық модельді құру кезінде модельдеу объектісін эксперименттік зерттеу кезінде анықталған физикалық заңдылықтар қолданылады. Мысалы, қан айналымының математикалық моделі гидродинамика заңдарына негізделген. Математикалық модельдеу зерттеу әдісі ретінде бірқатар сөзсіз артықшылықтарға ие. Біріншіден, сандық заңдылықтарды математикалық тілде беру әдісінің өзі дәл және үнемді. Екіншіден, эксперименттік деректер негізінде тұжырымдалған гипотезаларды тексеру осы гипотеза негізінде құрылған математикалық модельді тексеру арқылы жүзеге асырылуы мүмкін. Ақырында, математикалық модель экспериментте немесе клиникада құру қиын осындай жүйелердің мінез-құлқын бағалауға, зерттелетін жүйенің жұмысын тұтастай немесе кез келген бөлек жүйенің жұмысын зерттеуге мүмкіндік береді. бөлігі[2.]
№1 мәселе. Бактериялар саны неше есе көбейетінін анықтаңыз
9 сағатта, егер 3 сағат ішінде олардың саны 100-ден 200-ге дейін өзгерсе.
Шешім. Бактериялардың көбею жылдамдығы, егер олар үшін азық-түлік жеткілікті болса және басқа да қажетті сыртқы жағдайлар жасалса (мысалы, бактериялардың басқа түрлермен басылуының болмауы) олардың санына пропорционалды екендігі эксперименталды түрде анықталды. Қазіргі уақытта қол жетімді бактериялардың саны х, содан кейін олардың санының өзгеру жылдамдығы болсын:
Бактериялардың көбею жылдамдығы олардың санына пропорционал болғандықтан, мынадай k болады:
Дифференциалдық теңдеудегі айнымалыларды ажыратамыз:
Интеграциялау арқылы біз аламыз:
Потенциализациядан кейін ол береді:
С табу үшін бастапқы шартты қолданамыз: t = 0 х = 100. Бізде: Се˚ = 100, С = 100, демек, х = 100 экт.
e k коэффициенті шарттан табылады: t = 3 x = 200 кезінде. Бізде:
Ізденген функция:
t = 9 x = 800 кезінде.
Жауап. 9 сағатта бактериялар саны 8 есе артады.
Заттың өсу жылдамдығы материяның қолда бар мөлшеріне пропорционал болатын заң табиғи өсу деп аталатын заң екенін ескеріңіз. Колониядағы микроорганизмдер санын уақытқа байланысты өзгерту процесінің бұл математикалық моделі өте жоғары болжаммен (қоректену мен тіршілік ету ортасының шексіз ресурстарымен және түраралық күрестің болмауымен) алынды. Табиғатта шын мәнінде бар колониялардың ешқайсысында мұндай өсуді байқау мүмкін емес. Табиғи өсу заңы нақты процеске қаншалықты сәйкес келеді деген сұраққа эксперименттік сынақ арқылы жауап беріледі. Әлбетте, кейбір ішкі жиындарда деректер үлгімен жақсы сәйкес келеді және модельдің өзін болжау үшін пайдалануға болады. 1845 жылы Верхульст - Перл микроорганизмдердің түр ішілік күресін ескеретін теңдеу алды. Түр ішінде қоректенуге және таралу орнына, сондай-ақ ауруларға байланысты бәсекелестік нәтижесінде өсу қарқыны төмендейді. Жалпы алғанда, өсімшенің төмендеуі х және Δx-тің кейбір жаңа функциясы болып табылады, біз оны b (x, Δx) деп белгілейміз. Бәсекелестік нәтижесінде индивидтер санының азаюы неғұрлым көп болса, соғұрлым жеке адамдар арасындағы кездесулер саны көп болады, яғни хх көбейтіндісіне пропорционалды, яғни х2. Осылайша,
b (x, Δx) = δ x2 Δt.

Содан кейін

Δх = ε х Δt - δ х2Δt.

Мұндағы ε - популяцияның меншікті (туа біткен) көбею коэффициенті, δ - түр ішіндегі бәсекелестік коэффициенті. Соңғы теңдеудің екі жағын да Δt-ге бөліп, шекке өте отырып, аламыз Бұл Верхульст-Перл теңдеуі. Бұл теңдеудің математикалық түрлендірулерден және t0 = 0 және x (0) = x0 кезіндегі ε δ = h белгілеуінен кейінгі шешімі.
№2 мәселе. Егер таңғы сағат 6-да бұл аудан 1600 см2 болса, сол күні сағат 6-да шеңбер пішінді ағаш жапырағының ауданы арасындағы байланысты табыңыз. - 2500 см2.
Шешім. Парақтың ауданы дөңгелек, яғни парақтың шеңберіне пропорционал. Жапырақ алаңының ұлғаю жылдамдығы оған түсетін күн сәулесінің мөлшеріне пропорционалды[3].
Күн сәулесінің мөлшері, өз кезегінде, жапырақтың ауданына және сәулелердің бағыты мен тігінен жапырақтың арасындағы бұрыштың косинусына пропорционал.

Күн сәулесінің бағыты арасындағы бұрышты алайық
ал вертикаль таңғы сағат 6-да және 18-де 90 °,
ал түсте - 0 °.
Түн ортасынан бастап есептелген уақыт t болсын. Егер S айнымалы жапырақ ауданы болса, онда жапырақтың өсу жылдамдығы:
мұндағы 2PIr - парақтың шеңбері, Q - күн сәулесінің мөлшері, k1 - пропорционалдық коэффициент.
Жапырақ ауданы S = PIr2, қайдан:
Содан кейін:
Шарты бойынша
Q = k2 S cos α,
мұндағы α - сәулелердің бағыты мен вертикаль арасындағы бұрыш, k2 - пропорционалдық коэффициенті.
α бұрышы t аргументінің сызықты өсетін функциясы:
α = k3 t + b.
k3 және b параметрлері қосымша шарттардан табылады:
t = 6 α = -PI 2 кезінде,
t = 12 α = 0 кезінде,
t = 18 α = PI 2 кезінде.
Соңғы екі шарттан бізде:
0 = 12k3 + b,
PI 2 = 18k3 + b.
Бұл жүйені шеше отырып, біз аламыз:
k3 = PI 12, b = - PI.
Демек,
(2) α мәнін ауыстырсақ, бізде:

Q = k2 S cos [PI (t - 12) 12].

(1) теңдеуден аламыз:
Біз k = k1k2 орнаттық. Айнымалыларды бөлгеннен кейін бізде
Интеграциялау арқылы біз аламыз:
Бастапқы шарттардан (t = 6 S = 1600, t = 18 S = 2500 кезінде) бізде:

Бұл жүйені шеше отырып, біз аламыз:
Бұл мәндерді (3) орнына қойсақ, біз мынаны аламыз:
мұнда:
Жауап. Шеңбер пішіні бар ағаш жапырағының ауданы арасындағы уақытқа тәуелділік (4) формуламен өрнектеледі.
№3 есеп. Ағаштың биіктігі мен оның өсу уақыты арасындағы байланысты табыңыз.
Шешім. Ең қолайлы жағдайлардың өзінде барлық ағаштар, түріне қарамастан, бастапқыда тез өсетіні белгілі, содан кейін олардың өсуі баяулайды, ақырында ол мүлдем тоқтамайды.
Тәждің өсуімен, бір жағынан, фотосинтезге байланысты энергия ағыны артады, ал екінші жағынан, мысалы, қоректік заттарды тасымалдаумен байланысты қиындықтар, демек, мұндай қажеттіліктерге энергия шығыны артады. . Ақыр соңында, энергия ағыны шығындарды жабуға жеткіліксіз және ағаш өсуін тоқтатады.
Осы пайымдаулардың негізінде негізгі болжамдарды тұжырымдауға болады, оның негізінде энергия балансының теңдеуін құрастыру негіз болады, яғни математикалық модель құрастырылады.
Жетілген өсімдік өсу процесінде геометриялық ұқсастықты сақтайды, яғни жетілген өсімдікте геометриялық өлшемдердің қатынасы өскен сайын өзгермейді, мысалы, биіктіктің диаметрге қатынасы және т.б.
Ағаш бос энергияны (немесе белсенді затты) тек фотосинтез арқылы алады.
Бос энергия фотосинтезге, тірі ұлпаның құрылысына (өсуіне) және топырақтан ерітіндіні көтеруге жұмсалады. Орташа алғанда, ұзақ уақыт бойы зауыт бірлік бетіне тұрақты жарық мөлшерін алады және шексіз қордан қажетті заттарды сіңіре алады. Энергия балансының теңдеуін құрастырайық.
Өсімдіктің сызықтық өлшемін x арқылы белгілейік, онда өсімдіктің биіктігі х, жапырақтардың беті х2, өсімдік көлемі х3 мәнімен өрнектеледі және х өзгереді. уақыт бойынша: x = x (t). Сонымен қатар, x (t0) = 0 болсын. Энергетикалық баланс теңдеуіне кіретін барлық шамаларды х арқылы өрнектеп көрейік.
Алдымен келіп түсетін бос энергияның өрнегін табайық E. Бұл энергия өсімдіктің жасыл бөлігіндегі фотосинтез нәтижесінде пайда болады, ал жасыл бөлігінің беті неғұрлым үлкен болса, жасыл бөлігінің беті соғұрлым үлкен болады. Осылайша, Е-ні х2-ге пропорционал деп есептей аламыз:

Е = α х2,

мұндағы α - пропорционалдық коэффициенті, ол жапырақтардың өлшемі мен пішініне және фотосинтездің қарқындылығына байланысты. Біздің болжамымыз бойынша, басқа энергия көздері жоқ.[2]
Енді энергияны тұтынуды бақылап көрейік. Ең алдымен, энергия фотосинтез процесінің қажеттіліктеріне жұмсалады. Бұл ағын жылдамдығы да х2-ге пропорционал және оны β x2 деп жаза аламыз, мұндағы β α - белгілі бір пропорционалдық коэффициент.
Одан әрі энергия қоректік ерітіндіні өсімдіктің барлық бөліктеріне тасымалдауға жұмсалады. Бұл тұтыну неғұрлым көп болса, тасымалдау маршруттары, яғни зауыттың көлемі соғұрлым көп болатыны анық. Сонымен қатар, бұл тұтыну ауырлық күшін жеңумен байланысты және, демек, неғұрлым көп болса, қоректік заттардың биіктігін көтеру керек. Осылайша, бұл ағын жылдамдығы x3 және x екеуіне де пропорционалды, яғни. γ x3 x тең.
Ақырында, энергия зауыттың массасын арттыруға жұмсалады. Бұл тұтыну өсу қарқынына пропорционалды, яғни уақыт бойынша m = ρх3 массасының туындысы (ρ - өсімдіктің орташа тығыздығы, x3 - көлем).
Энергияның сақталу заңы бойынша энергия шығыны оның түсуіне тең болуы керек:
немесе
Бұл қалаған баланстық қатынас.
Теңдеудің екі жағын 3δρx2-ге бөліп, белгілейміз
Біз алып жатырмыз:
Дифференциалдық теңдеуді келесі түрде қайта жазамыз
Содан кейін
Туынды dx dt 0 екенін ескеріңіз, өйткені ағаштың өсуі өседі.
Демек, a - bx2 0, демек, x2 a b, яғни тікелей интегралдау әдісін қолдануға болады (x│ │с│ үшін теңдік орындалады:
Сонда бізде:
Бастапқы шарт х (t0) = 0, яғни С = - t0 және, демек
Бұл теңдеуді x үшін шешкенде, бізде:
Алынған формула (5) ағаш өсу қисығын береді. Егер сіз a, b және t0 (бұл мәндер ағаш түріне байланысты) білсеңіз, онда сіз осы түрдегі ағаштың орташа биіктігін оның жасына байланысты есептей аласыз. Жауап. Ағаштың өсуінің оның өсу уақытына тәуелділігі (5) формуламен өрнектеледі[4].

1.2. Биологиядан есептерді шығару әдістемесі. 9-сынып.

Молекулалық биология мәселелері
ДНҚ орнында 30 аденил нуклеотиді бар, бұл нуклеотидтердің жалпы санының 20% құрайды. Осы ДНҚ молекуласының сапалық және сандық құрамын анықтаңыз. Берілген ДНҚ молекуласында спиральдың неше айналымы бар (спиральдың 1 айналымы - 10 негіз жұбы).
Берілгені: A = 30 (20%), табыңыз: Т-? G -? C -? бұрылады -?
Шешуі: 1) A = T, G = C (Чаргафф ережесі бойынша). A + T = 30 + 30 = 60 - бұл 20% + 20% = 40%
A + G + T + C = 100%. Біз пропорцияны жасаймыз:
60 нуклеотид (A + T) - 40%
X нуклеотидтері (A + T + C + G) - 100%
X = 60 x100 40 = 150 нуклеотидтер
C + G = 150-60 = 90; C = G = 902 = 45.
2) бері Бір айналымда 10 жұп, содан кейін берілген ДНҚ молекуласында:
15020 = 7,5 айналым. Жауабы: T = 30, G = 45, C = 45; 7,5 айналым.
1.2.ДНҚ молекуласының орнында 20 аденил нуклеотидтері бар, бұл нуклеотидтердің жалпы санының 10% құрайды. ДНҚ молекуласының осы бөлімінің сапалық және сандық құрамын анықтаңыз
Егер ДНҚ молекуласының бөлімінде 20 аденил нуклеотид болса, бұл олардың жалпы санының 10%, онда комплементарлылық принципі бойынша нуклеотидтердің бірдей саны (20) тимилнуклеотидтерге келеді[5].
(сонымен қатар 10%), бұл 100% 20% құрайды. Бұл 80% цитидил (40%) және гуанил (40%) нуклеотидтерге түсетінін білдіреді.

20% ------------ 40 нуклеотид болса

онда 100% --------------- х нуклеотидтер, демек х = 200 нуклеотидтер (100 цитидил және 100 гуанил нуклеотидтер. ДНҚ-ның осы аймағында барлығы 240 нуклеотидтер.
1.3.ДНҚ молекуласының орнында 30 тимидил нуклеотидтері бар, бұл нуклеотидтердің жалпы санының 10% құрайды. ДНҚ молекуласының осы бөлімінің сапалық және сандық құрамын анықтаңыз.
Тимидил саны = аденин саны
Гуанин саны = цитозин саны
Егер 30 тимидил 10% болса, аденин де 30 және 10%,
100% - (10% + 10%) = 80% G және C бірге, яғни 80% 2 = 40% - G, және 40% - C,
Егер 10% = 30 болса, онда 100% = 300, сәйкесінше G-40% немесе 120, ал C да 40% немесе 120.
Жауабы: A = 30 T = 30 G = 120 C = 120
1.4.ДНҚ кодтау тізбегіндегі нуклеотидтер тізбегі келесідей: A-A-T-G-G-A-T-T-T-Ts-Ts-A. Осы ДНҚ орнында кодталған ақуыздың биосинтезіне қатысатын т-РНҚ антикодондарындағы нуклеотидтер тізбегін анықтаңыз.
Комплементарлылық принципі бойынша ДНҚ тізбегін таңдаймыз: A-A-T-G-G-A-T-T-T-Ts-Ts-A
i-РНҚ: U-U-A-C-U-A-A-A-G-G-U
біз комплементарлылық принципі бойынша т-РНҚ құрастырамыз: AAU, GGA, UUU, CCA
1.5.ДНҚ молекуласының орнында 40 тимидил нуклеотидтері бар, бұл жалпы санның 20% құрайды. ДНҚ молекуласының осы бөлімінің сапалық және сандық құрамын анықтаңыз.
T = A
C = G, ДНҚ молекуласында нуклеотидтердің барлық 4 түрі 100% құрайды.
Тимин 20% болса, аденин 20%:
20% + 20% = 40% (T + A бірге) бұл: 40 + 40 = 80 нуклеотид.
Пропорцияны шығарайық:
40% - 80 нуклеотидтер (T + A)

100% - X нуклеотидтері (A + T + G + C); X = 100% x 8040 = 200
C + G = 200 - 80 = 120; C = G = 1202 = 60
Жауабы: А-40, С-60, Г-60.
1.6 Хабаршы РНҚ молекуласындағы нуклеотидтер тізбегі келесідей: A-A-C-G-C-C-U-G-C-U-C-G. Көрсетілген м-РНҚ молекуласы транскрипцияланған ДНҚ молекуласындағы (екі тізбектегі) нуклеотидтер тізбегін қалпына келтіріңіз[6].
i-РНҚ: A-A-C-G-C-C-U-G-C-U-C-G
1-ші ДНҚ тізбегі: T-T-G-C-G-G-A-C-G-A-G-C
2-ші ДНҚ тізбегі: A- A-C-G-C-C-T-G-C-T-C-G
1.7 Генетикалық код кестесін пайдалана отырып, ақуыздағы аминқышқылдарының тізбегін қалпына келтіріңіз, ол туралы ақпарат сенсорлық ДНҚ тізбегінің келесі нуклеотидтік тізбегінде кодталған: A-T-G-A-A-A-T-T-T-Ts-Ts-A (билетте берілген кесте).
Тізбекті үштікке бөлейік: ATG-AAA-TTT-TsTSA. Генетикалық код кестесін пайдалана отырып, белоктағы аминқышқылдарының ретін табамыз: Тирозин-лейцин-лизин-глицин.[4]

1.2 Биологиядан шығармашылық тапсырмалар және оларды шешу әдістері

Сіз құсты торда ұшуға үйрете алмайсыз. Ашық тапсырмалардың ашық кеңістігіне шықпай, шығармашылық бұлшықетті өсіру мүмкін емес - шешуге әртүрлі тәсілдер, мәселенің мәнін тереңдетудің әртүрлі дәрежесі, әртүрлі жауаптар. Психологтар ойлаудың екі түрін ажыратады: конвергентті (жабық, шығармашылық емес) және дивергентті (ашық, шығармашылық). Конвергентті ойлау басым тұлға типі интеллектуалды, дивергентті -- креативті деп аталады. Зияткер тіпті өте күрделі мәселелерді шешуге дайын, бірақ біреулер қойған және белгілі технологиялары бар шешімдер - жабық мәселелер деп аталады. Шығармашылық, керісінше, міндеттерді өзі көре және қоя алады, тар белгіленген жағдайдан шығуға ұмтылады ...

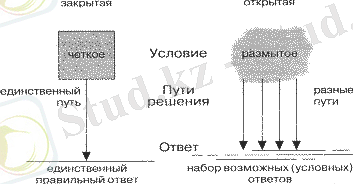
Шын мәнінде, әр адамның интеллектуалдық және шығармашылық қабілеттері бар, бірақ әртүрлі дәрежеде. Шығармашылық ойлау есейген сайын жоғалады. Жоғары сынып оқушылары мен студенттердің басым көпшілігі конформды, тәуелсіздіктен қорқады, түпнұсқа идеяларға емес, шайнап алынған және қатаң түрде сөрелерде сұрыпталған ақпаратқа құмар. Шарттардың белгісіздігі және шығармашылық мәселені шешудің өзгермелілігі оларды қорқытады. Есептік есептерді бірінші жуықтау бойынша 2 класқа бөлуге болады: 1) конструктивті тип (тікелей есептер) және 2) түсіндірмелі тип (кері есептер). Тікелей мәселе былай тұжырымдалады: оны шешу үшін қандай да бір сыртқы әсерді қажет ететін проблемалық жағдай беріледі; сіз білуіңіз керек - қайсысы? Кері есептің мәні - сол немесе басқа құбылыстың, процестің себебін (түсіндірмесін) ашу. Ойлау операциялары тұрғысынан алғанда конструктивті типтегі тапсырмалар негізінен синтетикалық, түсіндірмелі типтегі тапсырмалар аналитикалық сипатта болады. Жалпы конструкторлық тапсырмалардың мақсаты - адамның кез келген қажеттілігін қанағаттандыру, оған қажетті функцияны орындау (бұл жүйенің жұмыс істеуінің ең жақсы принципін іздеуді білдіреді) ең жақсы жолын табу. Олар шешімдерді іздеудің максималды белгісіз аймағымен, анық емес бастапқы және шекаралық шарттармен және (көбінесе) ақпараттың жетіспеушілігімен сипатталады. Мұндай жағдайда шешімді кездейсоқ табу әдістерін қолданған жөн, мысалы, миға шабуыл[7].
Мысалға. Әдетте, жеміс ағаштары үлкен тәжге ие болу үшін өсіруге тырысады: ол неғұрлым үлкен болса, соғұрлым көп өнім болады. Дегенмен, бірден мәселе туындайды: кең таралған бұтақтар жемістің салмағына төтеп бере алмайды және бұзылады. Бұған жол бермеу үшін олар әртүрлі реквизиттер қояды. Бірақ бұл, өз кезегінде, ағаштар мен олардың астындағы топыраққа қол жеткізуді қиындатады, тіректер қабығын ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.