аНЫҚТАУЫШТАР

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

Алғыс сөз.

Математика - нақты дүниенің кеңістіктік пішіндері мен сандық қатынастары туралы ғылым. Математика атауы гректің mathema - білім деген сөзінен шыққан. Уақыт өткен сайын математика үйренетін кеңістіктік пішіндер мен сандық қатынастар үзіліссіз кеңеюде, сондықтан берілген анықтаманы кең магынада түсіну керек. Кеңістіктік пішіндері негізінен геометрия (грек тілінен аударғанда гео - жер, метрия - өлшеу) ғылымы, ал сандық қатынастарды арифметика, алгебра (арабтың “аль-джабр” - теңдіктің теріс мүшелерін бір бөлігінен басқа бөлігіне өткізу), математикалық талдау, есептеу математикасы жэне соңғы кезде пайда болған көптеген салалар зерттейді. Математиканың дамуын шартты түрде төрт кезеңге бөлуге болады: алғашқы ұғымдардың пайда болуы (сан, қарапайым геометриялық пішіндер) және көптеген деректердің жиынтыгының қалыптасуы; элементар математика; айнымал шамалардың математикасы; есептеу математикасы мен есептеу техникасына негізделген қазіргі заман математикасы. Адамзаттың іс-тәжірибе қызметінде және шаруашылық мәселелері негізінде жинақталған деректер математиканың өзінше ерекше ғылым екендігін түсінуге эсер етті. Бүл элементар математиканың бастапқы кезеңі еді жэне ежелгі Грекияда жаңа эраға дейін VI-V ғасырларда қалыптасты. Уақыт өте математика гылым ретінде сапалы түрде жетіле түсті. Элементар математика дәуірі басталды. Әдетте элементар математика деп элементар арифметика, ежелгі Грекияның ұлы геометрі Евклидтің еңбектерінде толық қамтылған элементар геометрия, Индия, Аравия, Орта Азия (Эл-Хорезми, Эл-Фараби) математиктерінің жетістіктерін ары қарай жалғастырып дамытқан Еуропа математиктерінің еңбектерінде, XVI ғасырда негізінен аяқталған элементар алгебра түсініледі. Элементар математика негізінен тек түрақты шамаларды зерттейді. Демек элементар математика үнемі өзгерістегі материалдық дүниенің күрделі заңдарын, бір-бірімен өзара алуан түрлі жэне жан-жақты байланыста өтіп жататын құбылыстарын зерттеудің қуатты қүралы бола алмайды. XVII гасырда жаратылыстану мен техника талаптары қозғалысты математикалық түрғыдан айнымал шамалардың өзгеру процесін, геометриялық фигураларды түрлендіруді үйрену мақсатында жаңа әдістер құруға алып келді. Әмбебап Декарт координаталар әдісі негізінде аналитикалық геометрияның пайда болуы, геометриялық мэселелерді алгебра және математикалық талдау тіліне көшіруге және, керісінше, алгебра жэне аналитикалық деректерді геометриялық түрғыдан түсіндіруге мүмкіндік берді. Айнымал шамаларды аналитикалық геометрияда қолдану, дифференциалдык жэне интегралдық қисаптардың құрылуымен айнымал шамалардың математикасының кезеңі басталды. Бүл кезеңде бұрынғы түрақты шамалар мен сандар орнына негізгі үғым ретінде функция үғымы алынды. Функцияны 4 үйрену математикалық талдаудың негізгі ұғымдарына алып келді: шек, туыңды, дифференциал жэне интеграл. Математиканың өзінің іштей дамуы, ғылым мен техниканың әртүрлі салаларын “математикаландыру”, математикалық эдістердің көптеген істэжрибе жұмыстарына енуі жэне есептеуші математика мен дискреттік математика негізінде жүзеге келген есептеуші техниканың дамуы қазіргі заман математикасының іргетасы болып табылады. Бұлар негізінде жаңа математикалық пәндер - операцияларды зерттеу, ойындар теориясы, математикалык экономика жэне т. б. дүниеге келді. Математикада жаңа теориялар тек жаратылыстану, техника жэне экономиканың қажеттілігінен ғана емес, математиканың өзінің ішкі қажеттілігінен де пайда болады. Мысалы, Лобачевский геометриясы. Жалпы әлем екі кұрылымнан тұрады: макроэлем, микроәлем. Макроэлемнің негізінде үзіліссіздік принципі жатады. Яғни макроәлемдік нэрсе үзіліссіз қозғалыста болады жэне оның орнын, жылдамдығын дэл анықтауға болады. Микроәлем негізінде аныкталмағандық принципі жатады, яғни элементар бөлікше қозғалыста болғанда оның орны белгілі болса, жылдамдығы белгісіз, ал жылдамдығы белгілі болса, орны белгісіз болады. Сондықтан микроэлемдегі кұбылыстар жалпыланған функция ұғымы негізінде зерттеледі. Математикалық теорияны құрудың негізінде аксиоматикалык әдіс жатады. Мүнда теорияның іргесіне ақиқат ретінде бастапқы ережелер жүйесі - аксиомалар дэлелсіз қабылданады. Ал теорияның тұжырымдары осы аксиомалардьщ логикалық нәтижесі ретінде алынады. Мысалы, Евклид геометриясында теорияның негізгі мазмұны ақиқаттығы айкын бірнеше аксиомалардьщ негізінде дедуктивтік жолмен алынған. Математикада ой қортындылаудың екі түрі бар: дедукция, индукция. Дедукцияда жалпы тұжырым негізінде нақты дербес жағдай үшін ой қортындыланады, ал индукцияда дербес жағдайлардан жалпы ой тұжырымдалады. Соңғы жағдайда математикалық индукция принципі қолданылады: егер Л(1) дұрыс болып, кезкелген п е N үшін А(п) түжырымның дүрыстығынан А(п + 1) түжырым да дұрыс болса, онда А(п) түжырымның дұрыстығы дәлелденген болады. Математикалык зерттеудің негізгі әдісі - математикалык дәлелдеу, яғни формальдық логиканың зандарына сүйеніп, қатаң логикалык тұжырымдау. Математикалык тұжырымдарды дәлелдегенде қажетті жэне жеткілікті шартгар кеңінен қолданылады. Қажетті шарттар орындалмаса, қарастырылатын Т тұжырым дұрыс емес, ал жеткілікті шарттар орындалса Т тұжырым дұрыс. Демек, жеткілікті шарттар қажетті шарттардың бөлігі. Математикада қүбылыстардың математикалык модельдері зерттеледі. Бір математикалык модель эртүрлі қүбылыстарды бейнелеуі мүмкін. Өйткені математикада қарастырылатын қүбылыстардың табиғаты емес, олардың 5 құраушыларының арасындағы қатынастар маңызды. Мысалы, бүкіл әлемдік тартылыс заңы мен Кулон заңы бірдей математикалық өрнекпен өрнектеледі. Математиканы оқытудың мақсатттары: белгілі бір деңгейде білім алу; үйренген математикалық эдістерді қолдана білу; математикалық ойлау жүйесі интуицияны дамыту; математикалық мәдениетті тәрбиелеу. Қазіргі ғылыми-техникалық революция дэуірі - ғылым, техника, экономика жэне басқаруды математикаландыру дэуірі. Қазіргі заманғы ғылыми қызметкер, инженер немесе экономист математиканың негіздерін біліп қана қоймай, ол өз саласында қолданылатын зерттеудің математикалық эдістерін терең игеруі керек. Әрбір ғылым өзінің шыңына математиканы қолданғанда ғана жете алады.

Мазмұны.

Алғыс сөз . . . 2

Мазмұны . . . 4

Матрицалар сақинасы. Матрицаларға қолданатын амалдар . . . 5

Сызықтық амалдардың қасиеттері . . . 6

Матрицаларды аудару амалы . . . 7

Матрицаларды көбейту амалы . . . 8

Анықтауыштар . . . 9

Анықтауыштардың негізгі қасиеттері . . . 10

Кері матрицаларды есептеу Гаусс-Жордан тәсілі . . . 11

Векторлық алгебра . . . 12

Векторларға амалдар қолдану . . . 13

Векторлар жүйесінің сызықты тәуелділігі мен тәуелсіздігі. Қасиеттері. База . . . 14

Екі вектордың скаляр көбейтіндісі . . . 16

Екі вектордың векторлық көбейтіндісі . . . 18

Үш вектордың аралас көбейтіндісі . . . 22

Жазықтықтағы түзудің теңдеулерінің түрлері . . . 25

Екі нүкте арқылы өтетін түзудің теңдеуі . . . 27

Жазықтықтағы екі түзудің өзара орналасуы және арасындағы бұрыш. 28

Эллипс және оның канондық теңдеуі . . . 31

Гипербола және оның канондық теңдеуі . . . 32

Екінші ретті қисықтың жалпы теңдеуі . . . 37

Функция. Кері функция. Күрделі функция. Параметрлік түрде берілген функция. Айқын емес функция. Функция графигі . . . 40

Алғашқы функция, анықталмаған интеграл, оның қасиеттері.

Анықталмаған интеграл кестесі. Анықталмаған интегралды

интегралдау әдістері . . . 42

Алғашқы функция табудың негізгі тәсілдері . . . 46

Рационал өрнектерді интегралдау . . . 48

Анықталған интеграл . . . 50

Бірінші текті меншіксіз интегралдар ұғымы . . . 53

Меншіксіз интегралдың абсолюттік және шартты жинақтылығы . . . 55

Анықталған интегралдың физикада, геометрияда қолданылуы.

Ауданды, көлемді, беттің ауданын, қисық ұзындығын, массаны табу. 57

Пайдаланылған әдебиеттер . . . 60

Матрицалар сақинасы. Матрицаларға қолданатын амалдар.

k жолы және n бағаны бар элементтері математикалық объекттерден тұратын кестені матрица деп атайды, арқылы белгілейміз.

Матрицалардың элементтері R нақты сандар мен C комплекс сандар жиындарынан және p-жай сан, қалындылар кластарынан алынуы мүмкін. Элементтері P өрісінен алынған, жолдар саны k-ға, ал бағандар саны n-ге тең болатын барлық матрицалар жиынын арқылы белгілейміз. Кейде матрицаның жолдар саны k-ға, ал бағандар саны n-ге тең деудің орнына біз қысқаша оның өлшемі ға тең дейміз.

Өлшемдері бірдей және сәйкес элементтері өзара тең болатын матрицалар тең деп аталады.

Матрицаларға бірнеше амалдар қолданылады, олардың арасында екі амал мүшелеп жасалынады. кез келген матрицалар, ал қандайда бір элемент болсын. Өлшемі ге тең, элементтері (немесе ) болатын матрицаны A мен B -ның қосындысы (сәйкес А-ның коэффициентіне көбейтіндісі) деп атаймыз. Осы екі амалдың біріккен аталуы сызықтық амал болады.

Сызықтық амалдардың қасиеттері

Кез келген және кез келген үшін келесі арақатынастар орындалады:

Қасиет 1. -қосу амалы коммутативті.

Қасиет 2. -қосу амалы ассоциативті.

Қасиет 3. қатысы орындалатындай жиынына тиісті О матрицасын табуға болады.

Қасиет 4. Кез келген матрицасына теңдіктері орындалатындай матрицасы табылады.

Қасиет 5.

Қасиет 6.

Қасиет 7.

Қасиет 8.

ДӘЛЕЛДЕУ.

Анықтамаларға сүйенсек, біз осы қасиеттерді дәлелдеу үшін жоғарыдағы әрбір теңдіктің сол жағындағы және оң жағындағы матрицалардың сәйкес элементтерінің теңдігін көрсетуіміз керек. Қасиет 1, 2, 5-8 үшін дәлелдеулер бір жолмен жүргізіледі, сондықтан біз біреуін ғана мысал ретінде көрсетейік.

Қосу амалының ассоциативті екенін көрсету үшін, біз алдымен қандайда

Бір индекстер жұбы берілсін делік. Бұл жерде Сонан соң матрицасының i-ші жолы мен j-ші бағаны қиылысқан орындағы элементті қосу амалының анықтамасы бойынша табайық. Егер болса, онда сол элемент тең болады. Р өрісінде қосу амалы ассоциативті, демек, . Соңғы теңдіктің оң жағындағы өрнек матрицасының орындағы элементі болып табылады. Ендеше

О матрицасының элементтерін деп белгілесек, онда қасиет 3 қанағаттандыру үшін болуы керек. Демек Барлық элементтері P өрісінің нөлдік элементіне тең матрицаны нөлдік матрица деп атаймыз. Әрбір, жиыны өзінің нөлдік матрицасы болады. Дегенмен, осы нөлдік матрицалардың бәрін бір ғана О символымен белгілейміз. Оның себебі: әдетте, матрицаларға амалдар жасағанда олардың өлшемдері анық болады.

Кез келген матрицасы үшін оның элементтеріне P өрісінде қарама-қарсы болатын элементтерден құрылған матрицасы қасиет 4-тегі теңдіктеріне жарамды болады. D мен F -тың элементері бір-біріне қарама-қарсы болғандықтан, осы матрицалар да қарама-қарсы деп аталады.

Мысал 1. Келесі үш матрица берілген:

(1. 1)

матрицасын таба аламыз ба ? Егер C=A+B және D=A-B болса, онда C және D матрицаларын табыңыз.

А матрицасында 2 жол 3 баған бар, ал F матрицасында 2 жол 2 баған бар. Бұл екі матрицаның өлшемдері сәйкес емес, сондықтан оларды қоса алмаймыз, яғни матрицасы анықталмаған.

А және В матрицаларының өлшемдері сәйкес, яғни,

D=A-B матрицасын табайық:

Жауабы:, .

Мысал 2. матрицасы берілген. және матрицаларын табыңыз.

Жауабы:

Матрицаларды аудару амалы

Егер матрицасының жолдары мен бағандарының рольдерін алмастырсақ, онда n бағаны мен k жолы бар символымен белгіленетін матрица пайда болады. Демек, матрицасының i-ші жолы мен j-ші бағаны қиылысқан орнында А матрицасының элементі орналасады. Ендеше . Осы себептерден А матрицасына қарағанда матрицасы аударылған деп аталады, ал А матрицасын матрицасымен алмастыруды аудару амалы деп атайды.

МЫСАЛ. Егер

болса, онда болады. (1. 2)

Аудару амалының келесі қасиеттері анық:

Матрицаларды көбейту амалы

Матрицаларлы өзара көбейту амалы оларға қолданатын сызықтық амалдарға қарағанда күрделі болып көрінуі мүмкін. Біздің мақсатымыздың бірі матрицаларды көбейту амалының жасалуы бірнеше сызықтық амалдардың жасалуына пара-пар екендігін көрсету, сонымен қатар амалының күрделілігі тек қана сызықтық амалдар жасалу санына байланыстылығын айқындау.

Элементтері кез келген P өрісіне тиісті жолы мен бағаны берілсін. жолының бағанына көбейтіндісі деп, олардың сәйкес элементтерінің көбейтінділерінің қосындысына тең болатын P өрісінің элементін атаймыз. Жолды бағанға көбейту үшін олардың элементтер саны бірдей болуы қажет екендігі ақиқат.

Енді кез келген екі матрица берілсін. A матрицаның жолдарын деп белгілейік: (1. 3)

B матрицасының бағандарын деп белгілейік:

A матрицасының B матрицасына көбейтіндісі деп элементтері

формула бойынша есептелетін -ға тиісті матрица аталады. A матрицасының бағандар саны В-ның жолдар санына тең болмаса,

анықталмаған.

МЫСАЛ 1. - берілген матрицалар

матрицасын табуымыз керек. Алдымен С-ның өлшемін келесі ережемен табайық. А мен В -ның өлшемдерін қатарынан жазып, ортасындағы

екі тең сандарды алып тастасақ, шеткі екі сан көбейтіндінің өлшемін береді:

. Сонан кейін, С матрицасының элементтерін деп белгілесек, онда анықтама бойынша

Ендеше

Анықтауыштар.

А квадрат матрицасының элементтері, ал А-ның реті, яғни жолдары

мен бағандар саны n -ге тең болсын, яғни А матрицасының анықтауышын оның реті бойынша индуктивтік анықтама бойынша енгізейік. А -ның анықтауышын немесе арқылы белгілейміз.

Егер болса (индукциялық базисі), онда А матрицасының құрамында

жалғыз ғана элементі бар. Бұл жағдайда деп аламыз.

Индукциялық қадам болсын және (n-1) -ші ретті матрицалардың анықтауыштарын есептей аламыз деп ұйғаралық. Онда n-ші ретті A матрицасының анықтауышы деп

(2. 1)

формуласымен есептелетін P өрісінің элементін атаймыз. Бұл жерде және бұдан әрі біз арқылы А матрицасының i-ші жолы мен j-ші бағаны алынып тасталғаннан шыққан (n-1) -ші ретті матрицаның анықтауышын

белгілейміз. Жоғарыдағы формула анықтауыштың бірінші жолы бойынша жіктеу формуласы деп аталады.

2-ші ретті анықтауыш келесі формула бойынша есептеледі

(2. 2)

3-ретті квадрат матрицасының анықтауышын үшбұрыш

ережесімен есептейік. (2. 3)

Анықтауыштардың негізгі қасиеттері

Қасиет 1. Егер матрицаның екі жолының орнын алмастырылса, онда

оның анықтауышы бастапқы анықтауышқа қарама-қарсы болады.

Қасиет 2. Егер матрицаның екі жолы бірдей болса, онда оның

анықтауышы 0-ге тең.

Қасиет 3. Матрицаны аударғанда, оның анықтауышы өзгермейді:

Қасиет 4. Матрицаның кез келген жолының (бағаның) ортақ

көбейткішін анықтауыш таңбасының сыртына шығаруға болады.

Дербес жағдайда, егер матрицаның бір жолы (бағаны) нөлдік болса,

онда оның анықтауышы нөлге тең болады.

Қасиет 5. (анықтауыштарды қосу туралы теорема. ) Кез келген і үшін келесі теңдік орындалады :

Осы сияқты теңдіктер бағандарға да орындалады.

Қасиет 6. Егер матрицаның жолдары (бағандары) сызықтық тәуелді

болса, онда оның анықтауышы нөлге тең болады.

Қасиет 7. Матрицаның жолына (бағанына) басқа жолын (бағанын)

коэффициентке көбейтіп алып қосқанда, одан оның анықтауышы

өзгермейді.

Мысал 1. Анықтауышты есептеңіз:

Шешуі:

Жауабы: 1.

Мысал 2. Анықтауышты есептеңіз:

Шешуі:

Жауабы: 15.

Кері матрицаларды есептеу Гаусс-Жордан тәсілі

матрицасына матрицасы табылып

теңдігі орындалатын болса, онда A керіленетін матрица, ал В матрицасы A -ның кері матрицасы деп аталады. A матрицасына кері болатын матрица символымен белгіленеді, яғни .

матрицасы берілген. бірлік матрицасын алып, блокты матрицасын құрастырайық, оның өлшемі ге тең. Гаусс-Жордан алгоритмі келесі процедуралардан тұрады.

1. A матрицасының сол жақ жоғарғы бұрышынан бастап төмен қарай

жүргізіп блокты матрицасының жолдарын сатылы түрге келтіреміз. Нәтижесінде ретті шаршы матрицалардан құрастырылған блокты матрицасын аламыз.

2. Егер матрицасының соңғы жолы нөлдік жол болса, онда алгоритмді

нәтижесіз тоқтатамыз. Кері жағдайда келесі процедураға көшеміз.

3. матрицасының оң жағындағы төменгі бұрышынан бастап жоғары

қарай саны матрицасының жолдарына сатылы түрге келтіру

алгоритмін пайдаланып блокты матрицаға келеміз. Осы матрицаның блогы диагональ матрица болады.

4. блокты матрицасының жолдарын (b) типті элементар

түрлендірулерін пайдаланып блокты түріне келтіреміз. Алгоритмнің

нәтижесін D матрица болады.

Тұжырым 1. Егер Гаусс-Жордан алгоритмі нәтижелі болса, онда D

бастапқы A матрицасына кері матрица болады.

болсын. элементінің миноры деп, өрісінің ( элементі тұрған жолды және бағанды сызып алып тастағанда шыққан матрицаның анықтауышы) элементін атаймыз. элементінің алгебралық толықтауышы деп, өрісінің элементін атаймыз. Элементтері матрицасының элементтерінің алгебралық толықтауыштарына тең болатын және символымен белгіленетін матрицаны 퐴 −ға одақтас матрица деп атайды.

Мысал.

матрицасының керісін Гаусс-Жордан әдісімен шешіңіз.

Шешуі:

Олай болса, кері матрица: .

Жауабы: .

Векторлық алгебра

Анықтама. Бағытталған кесіндіні вектор деп атайды. Суреттегі

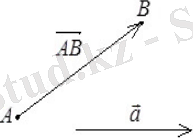вектордың басы 퐴, ал ұшы B деп аталады. Бағытталған кесіндінің ұзындығы вектордың ұзындығы немесе модулі деп аталады деп белгіленеді. (3. 1)

Анықтама. Басы мен ұшы бір нүктеде болатын вектор нолдік вектор

деп аталады, деп белгіленеді. Бұл вектор үшін екені түсінікті.

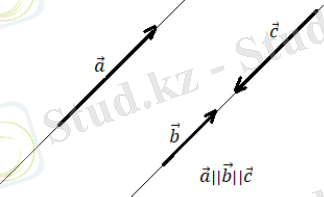Анықтама. Бір түзу бойында немесе параллель түзулер бойында орналасқан векторларды коллинеар векторлар деп атаймыз.

Келісімдер:

1) нөлдік вектор кез келген векторға коллинеар деп саналады:

∀ : ; (3. 2)

2) нөлдік вектор кез келген векторға перпендикуляр деп саналады: ∀ : ⊥ .

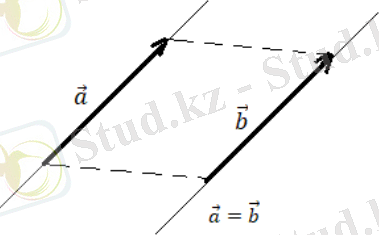Анықтама. Екі вектор мен тең деп аталады, яғни егер келесі шарттар орындалса:

;
= ;
↑↑ . (3. 3)

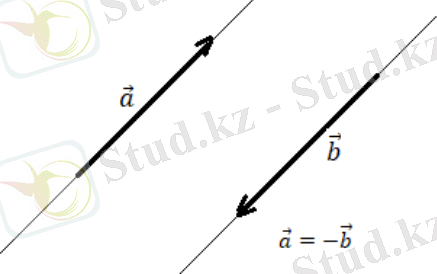Тең векторларды параллель көшіру арқылы беттестіруге болады. Егер соңғы анықтамада 1) мен 2) орындалып, ал 3) ↑↓ болса, онда мен қарама-қарсы векторлар деп атаймыз: = −.

(3. 4)

Векторларға амалдар қолдану

Қосу.

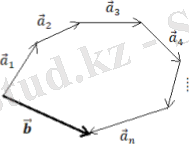Қасиеттері: (4. 1)

(

Санға көбейту. (4. 2)

саны мен векторы үшін векторы келесі шарттарға қанағаттандырады:

;

Бұл жерде, егер

Қасиеттері:

(4. 3)

Анықтама 푂푢 өсі мен векторын қарастырайық. 퐴 және 퐵 нүктелерінен 푂푢 өсіне перпендикулярлар түсіреміз.

Қиылысудан шыққан 퐴′ пен 퐵′ нүктелерін қосып вектор құрайық. векторы векторының 푂푢 өсіне түсірілген ортогоналды проекциясы деп аталады.

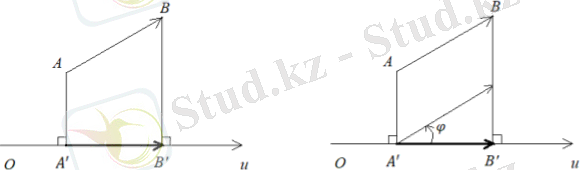
(4. 5)

Теорема (Векторлардың 1-ші коллинеарлық критерийі)

Векторлар жүйесінің сызықты тәуелділігі мен тәуелсіздігі. Қасиеттері. База.

Анықтама. бірнеше вектор (немесе векторлар жүйесі деп атайтын боламыз) және сандары берілсін. Егер болса, онда векторы векторларының сызықтық комбинациясы немесе өрнегі деп аталады.

Анықтама. векторлар жүйесі сызықты тәуелді деп аталады, егер олардың нолдік сызықтық комбинациясында ең болмаса бір коэффициент нолден өзгеше болса

Анықтама. векторлар жүйесі сызықты тәуелсіз деп аталады, егер олардың нолдік сызықтық комбинациясы тек қана барлық коэффициенттері нолдік болғанда мүмкін болса

Қасиеттері:

1) Егер векторлар жүйесінде нольдік вектор бар болса, онда ол жүйе сызықты тәуелді болады.

2) Егер векторлар жүйесінде екі тең вектор бар болса, онда ол жүйе сызықты тәуелді болады.

3) Егер сызықты тәуелді векторлар жүйесіне бірнеше вектор қоссақ, онда шыққан жаңа жүйе сызықты тәуелді болады.

4) Егер сызықты тәуелсіз векторлар жүйесінен бірнеше вектор алсақ, онда

шыққан жаңа жүйе сызықты тәуелсіз болады.

5) Векторлар жүйесі сызықты тәуелді болу үшін, векторлардың ең болмаса біреуі қалғандары арқылы өрнектелуі қажетті және жеткілікті.

6) сызықты тәуелсіз, ал сызықты тәуелді болсын. Онда

Анықтама. Кеңістіктегі максималды сызықты тәуелсіз векторлар жүйесі база (базис) деп аталады.

Анықтама. Вектордың база бойынша жіктелген кездегі коэффициенттер координаталар деп аталады.

Базадағы векторлар саны кеңістіктің өлшемділігін береді.

векторлары кеңістігінде максималды сызықты тәуелсіз болсын, онда үшін, векторлар жүйесі сызықты тәуелді болады, ал 6-шы қасиет бойынша сандары:

Бұл сандар векторының базасындағы координаталары деп аталады.

Екі вектордың скаляр көбейтіндісі.

Анықтама. Келесі формула бойынша есептелетін санды екі вектордың және скаляр көбейтіндісі деп аталады:

(5. 1)

Ескерту. Екі вектордың арасындағы бұрыш дегеніміз екі вектордың басын бір нүктеге түйістіргендегі ең кіші бұруды айтамыз.

Теорема. (Векторлардың перпендикулярлық критерийі)

Дәлелдеуі.

1) (5. 2)

Қасиеттері:

Теорема. Тікбұрышты декарт координаттар жүйесінде екі вектордың

және скаляр көбейтіндісі келесі формуламен есептеледі (5. 3)

Дәлелдеуі.

Өйткені 4 қасиет бойынша ал перпендикулярлық критерийінен шығады.

Екі вектордың векторлық көбейтіндісі

Анықтама . Бас нүктелері бір нүктеге кондырылған компланар емес реттелген векторлар үштігі оң үштік деп аталады, егер векторының ұшынан қарағанда дан ға ең кіші бұру сағат тіліне қарама-қарсы болса, ал сағат тілімен орындалса сол үштік деп аталады.

(5. 4)

Егер оң (сол) үштік болса, онда үштіктері де оң (сол) болады; ал кез келген екі вектордың орнын ауыстырсақ, онда үштік өз атын өзгертеді, яғни, сол (оң) болады.

Анықтама . және векторларының векторлық көбейтіндісi деп символымен белгіленетін және келесі үш шартты қанағаттандыратын векторын айтады: