Механика бойынша

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 40 бет
Таңдаулыға:

Механика бойынша дәрістер курсы.
Материялық нүктенің қозғалысы

Материяның ең қарапайым қозғалысы денелердің және олардың жеке бөлшектерінің кеңістіктегі бір-біріне қатысты орын ауыстыруы болып табылатын механикалық қозғалыс. Егер дененің формасы мен өлшемдері оның қозғалыс тына елеулі ықпал жасамайтындай болса, ондай денелерді материялдық нүкте деп қарастыруға болады. Мәселен, мөлшерінің үлкендігіне қарамастан күнді жән еоны айнала қозғалатын планеталарды материялдық нүкте деп қарастыруға болады. Ал жердің өз осін айнала қозғалуын олай қарастыра алмайсың т.с.с.
Материялық нүкте қозғалысын қарастырған кезде ең алдымен есептеу жүйесін таңдап алу қажет, яғни қозғалысты қандай денемен салыстырып қарастыруды белгілейміз.
Z В С Қозғалатын материялық нүктенің жасаған
У сызығын траектория дейді. Ал оның белгілі
х у бір уақыт аралығында жүріп өткен кесіндісін
жол дейді.
x Қозғалыс түзусызықты болса траекториямен қозғала отырып уақыт аралығында жол жүрсе онда нүктенің орташа жылдамдығы
(1)
Орташа жылдамдықтан нүктенің лездік жылдамдығын анықтаймыз.
(2)
Сонымен траекторияның кез келген нүктесіндегі лездік жылдамдық сол нүктеге жүргізілген жанаманың бағытымен бағытталған, уақыттың нольге ұмтылу жағдайындағы орташа жылдамдықтың шекті мәніне тең.
.
Уақыттың өтуіне байланысты жылдамдығы өзгермейтін қозғалысты бірқалыпты, ал өзгермелі қозғалысты бірқалыпсыз қозғалыс дейді.
Егер жылдамдықтың өзгерісін деп алсам, онда дененің үдеуі
(3)
Бұдан лездік үдеу (4)
Сонымен траекторияның кез келген нүктесіндегі қозғалыстың лездік үдеуі деп уақыттың нольге ұмтылу жағдайындағы орташа үдеудің шекті мәнін айтады. ак
ац
Үдеу мс2 өлшемімен өлшенеді. Үдеу
векторы екі құраушыдан тұрады: олардың
а біреуі траекторияға жанама бағытымен
2-сурет бағытталған жанамалық немесе тангенсаль-
дық деп аталады, ал екіншісі траектория нүктесінің центріне қарай бағытталған центрге тартқыш үдеу деп аталады.
;
Жоғары математика түсініктерін пайдалана отырып (2) және (3) формулаға қатынастар шектерін туындымен айырбастап, былай жазамыз:
және :
Материалдық нүктенің бірқалыпты түзусызықты қозғалысында дене бірден уақыт аралықтарында бірдей жол жүреді. Сондықтан оның жылдамдығы өзгермейді.

Материалдық нүктенің түзусызықты өзгермелі қозғалысы кезіндегі үдеу:

Бұдан (5)
Мұндағы -бастапқы, уақыт моментіндегі жылдамдықтар.
Жолдың кез келген бөлігіндегі орташа жылдамдық:

Бұдан
(5) формуладағы мәнін орнына қойып, мынаны табамыз.

Бұдан (6)
(5) және (6) теңдеулерін біріктіріп шешсек
(7)
болып шығады.
Бірқалыпты баяу қозғалыс жағдайында
, .
Материялық нүктенің шеңбер бойымен қозғалысы
Бұл жағдайда дененің центрге тартқыш үдеуі:
.
Дененің бұрыштық жылдамдығы (10) ( с-1)
ац
(10) теңдеудің екі жағында R-ге көбейтіп
және екендігін ескеріп
(11)
екендігін анықтаймыз.

3-сурет
Материялық нүктенің шеңбердегі бір рет айналуына кеткен уақытты период деп, Т әрпімен белгілейміз, ал уақыт бірлігі ішіндегі жасаған айналым санын жиілік деп, әрпімен белгілейміз.
(12)
Жиілік Герцпен немесе сек-1 өлшемімен өлшенеді. (10) формуланы ескерсек
(13)
(10), (12) және (13) формулалaрдан
(14)
Горизантқа бұрыщ жасай лақтырылған дененің қозғалыс траекториясы, ауаның кедергісі ескерілмеген жағдайда парабола бойынша болады. Дене қозғалысының үдеуі тұрақты және уақыттың кез-келген моментінде g еркін түсу үдеуіне тең,ал жылдамдық векторы кез-келген нүктеде жанаманың бағыты бойынша бағытталады.
y Жылдамдықтың ОХ және ОУ остері бойынша
проекциялары
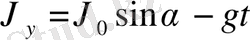g ; (15)
g g формулары бойынша, ал орын ауыстыру
x проекциялары
4-cурет ; (16)
формулары бойынша анықталады.
Тік жоғары лақтырылған дененің қозғалса жердің тарту күштің әсерінен болғандықтан бірқалыпты баяу қозғалысқа жатады.
; немесе (17)
Тербелмелі қозғалыс.Гармониялық тербелістер

Табиғат пен техникада дене қозғалысы белгілі бір уақыт аралықтарында ұдайы қайталанып отыратын жағдайлар жиі кездеседі. Мұндай қозғалыстарды тербелмелі қозғалыс немесе периодты тербелістер дейді.Әрбір тербеліске кеткен уақыт аралығын Т период дейді.
Тербелмелі қозғалыстардың ішінде ерекше орын алатын гармоникалық тербелістер. Олардың ең қарапайым мысалына серпінді пружина мен математикалық маятник тербелістері жатады.

Доғалық координаттары синустық немесе косинустық заң бойынша өзгеріп отыратын тербелістерді гармоникалық тербелістер дейді.

x ;
A ; (18)
Т 2Т t Тербеліс периодына кері шаманы тербеліс
жиілігі деп, әрпімен белгілейді.
. (19)
Тербеліп тұрған дененің тепе-теңдік қалыптан ең көп ауытқуының шамасын тербеліс амплитудасы дейді. (18) теңдеудегі шамасын тербелісфазасы дейді әрпімен белгілейді. Тербеліс фазасы тербеліп тұрған дененің тепе-теңдік қалыптан қандай бұрышқа бұрылғандығын көрсетеді.
(20)
(18), (20) теңдеулердегі дөңгелектік немесе циклдік жиілік деп аталады.
Гармоникалық тербеліс кезіндегі нүктенің жылдамдығы мен үдеуі.Тербеліп тұрған нүктенің ығысуының өзгеруі синусоидалық заң бойынша жүрсін:
(21)
Осы функциядан алынған туынды нүктенің жылдамдығын береді:
, (22)
мұндағы жылдамдық амплитудасы.
(22) теңдеуі уақыт бойынша дифференциялдап, үдеудің өзгеру заңын табамыз.
, (23)
мұндағы -үдеу амплитудасы.
болғандықтан (23) теңдеуі мына түрде жазуға болады:
(24)

Ньютон заңы. Масса және күш
Өткен жолы біз денелередің қозғалысын сол қозғалысыт тудырушы себептерін қарастырдық. Механиканың бұл бөлімін кинематика дейді. Енді денелердің қозғалысын оны тудырушы себептерімен бірге қарастыратын боламыз. Механиканың бұл бөлігін динамика дейді.
Динамиканың негізгі заңдары 18 ғасырдың 80-жылдары ағылшын ғалымы Ньютонмен тұжырымдалды. Бұл үшін ол адамзаттың ғасырлар бойы айтылған тәжірибелерді пайдаланды.
Ньютонның бірінші заңы инерция заңы деп аталады. Барлық денелер басқа денлердің әсері болмайынша өзінің тыныштық күйін немесе бірқалыпты түзусызықты қозғалысын сақтайды.
Тәжірибе әртүрлі денелердің бірдей әсер ету жағдайында әртүрлі жылдамдыққа және әртүрлі үдеуге ие болатындығын көрсетті. Бұл денелердің ең негізгі қасиеті массаға байланысты екендігін білдіреді. Сондықтан массаны инерттіліктің өлшеуіші деп санайды. Екінші жағынан массаның гравитациялық қасиеті де бар. Бұл жағдайда массаны тартылысытң өлшеуіші деп те атайды.
Денелердің массасы еркін таңдалып алынған эталондық дененің массасымен салыстыру жолымен анықталады. Халықаралық келісім бойынша мұндай эталон платинаиридиілік цилинрдің массасы. Ол Парижде сақталған. Оны 1 кг деп қабылдаған. Оның мыңнан бір үлесін грамм (г) дейді.
Бір дененің екінші денеге тигізетін әсері сол дененің күйін өзгертеді. Бұл әсер күш деген ұғымға ие болады. Тәжірибе әртүрлі күштердің әсерінен бір дене әртүрлі күштердің әсерінен бір дене әртүрлі үдеу алатындығын көрсетті.
Ньютонның екінші заңы. F күшінің әсерінен дененің алған үдеуі күш бағытымен бірдей бағытталған, ал шама жағынан сол күшке тура, дененің массасына кері пропорционал болады.
, бұдан (1)
СИ жүйесінде күш Ньютонмен өлшенеді.
1Н=1кг∙1мс2
Ньютонның үшінші заңы. Өзара әсерлеуші екі дене бір-біріне шама жағына тең, бағыты жағынан қарама-қарсы күштермен әсер етеді.
(2)
Ньютон заңдарының негізінде күш түсінігіне анықтама беруге болады.
Күш дегеніміз денелердің өзара әсерін және осы әсер нәтижесінде дененің үдеу алатындығын сипаттайтын физикалық шама.

Механикадағы күштер
Өзара әсерлесу табиғатына байланысты механикада әртүрлі күштер қарастырылады. Мәселен, тек тартылысқа байланысты гравитациялық табиғаты бар күштердің өзі үщеу: бүкіләлемдік тартылыс күші, салмақ күші, центрге тартқыш күш. Бұдан басқа бір дененің екінші дененің бетімен сырғи қозғалуына байланысты үйкеліс күші дененің деформациясына байланысты серпімділік күші қарастырылады.
Тартылыс күші. Табиғатта гравитациялық әсерлесудің бар екендігі және осы әсерлесу жайлы заң 1686 ж. Ньютонмен ашылды.(Натурал философияның математикалық бастамалары). Табиғаттағы бар денелерге тән қасиет-олардың бірін-бірі тартуы.
Екі материалық нүктенің біріне-бірі өзара тартылыс күші олардың массаларының көбейтіндісіне тура және арақашықтығының квадратына кері пропорционал.
(3)
мұндағы пропорционалдық коэффициент. Оның мәні тәжірибе жолымен анықталады және ол гравитациялық тұрақты деп аталады Бұл шаманы алғаш рет 1797 ж иірілмелі таразының көмегімен Кавендине анықтады.
Денелердің өзара тартылысы жүзеге асатын гравитациялық өріс-материяның ерекше түрі. Тегінде материяның екі түрі бар: зат және өріс. Бұлардың қасиеттерінің бір-бірінен айырмашылығы елеулі өрісті тудыратын зат. Екі дене әсерлескенде екеуі де өріс арқылы әсерлеседіү
Қазіргі кезде, космосты игеруге байланысты Жер серіктері мен космочтық кемелер Жерді белгілі бір қашықтықтан айнала қозғалады. Осыған байланысты (3) формулаға түзету енгізуге тура келеді.
(4)
мұндағы R-жер радиусы, M-оның массасы, m-космостық дененің массасы, h-оның жер бетінен қашықтығы, яғни биіктігі.
Салмақ күші. Гравитациялық күштерге дененің салмағы да жатады.

мұндағы жер бетіне жақын денелердің жерге еркін түсу үдеуі. Бір дене үшін тартылыс күштері бірдей болғандықтан
9,81 мс2
Центрге тартқыш күш. Дененің шеңбер бойымен бірқалыпты қозғалысы, бұрын айтқанымыздай центрге тартқыш үдеумен сипатталады. Осы үдеуге себеп болатын кез келген табиғаты бар күш центрге тартқыш күш деп аталады. Ол күш денеге түсірілген, шеңбердің центріне қарай бағытталған және Ньютонның екінші заңына сәйкес мынаған тең:
. (6)
мұндағы m-дененің массасы, ац-центрге тартқыш күш, мен сызықтық және бұрыштық жылдамдықтар, R-шеңбер радиусы.
Сызықтық және бұрыштық жылдамдықтар қозғалыс заңынан шығарылады.
және
Центрге тартқыш күш-денені шеңбер бойында ұстап тұратын күш. Бірақ жылдамдықтың өсуәне қарай дененің немесе оның бөлшектерінің центрден тебілуі де күшейді.Осыған құрғату машинасы, апаратор, центрден тепкіш сорғыш, дән тазалағыш машина сияқты центрден тепкіш механизмдердің жұмыстары негізделген. Мұны Ньютонның үшінші заңына сүйеніп түсіндіреміз. Денеге түсірілген центрге тартқыш күшпен қатар,онымен шама жағынан тең, ал бағыты жағынан оған қарама-қарсы центрден тепкіш күш әсер етеді.[
Серпінділік күш. Денеге түсірілген күш оны деформациялануы мүмкін. Оның нәтижесінде дененің ішінде деформациялаушы күшке қарсы әсер күш пайда болады. Ол күшті серпінділік күші дейді.
Денелердің деформациясының бірнеше түрі бар:созу, сығу, бұрау, ығыстыру,иілу. Олардың әрқайсысы серпінділік күш тудырады.
Кез келген кішігірім деформация кезінде пайда болатын серпінділік күші , деформация шамасына пропорционал болады.
(7)
мұндағы к-пропорционалдық коэффициент. Бұл жағдай Гук заңы деп аталады.Минус таңбасы серпінділік жүйенің дененің ығысуына қарсы бағытта болатындығын көрсетеді.
Егер деформациялаушы күш әсері тоқталғаннан кейін серпінділік күштер дененің алғашқы формасы мен мөлшерін толығымен қалпына келтіретін болса, ондай деформацияны серпінді деп атайды. Шамалы аз ығысу кезінде қалдық деформация пайда болады, дене өзінің бастапқы формасы мен мөлшерін қалпына келтіре алмайды.
Суретте көрсетілгендей білеушінің созылу кезіндегі
серпінде деформацияны қарастырайық. Оның
х төменгі жағына күш әсер еткен кезде ол
шамасына ұзарады. Ньютонның үшінші заңы
бойынша деформациялаушы күшке қарама-қарсы
серпінділік күші әсер етеді, яғни .
ұзару деформациялаушы күшке және алғашқы ұзындыққа тура және білеушінің ауданына кері пропорционал болады.
(8)
мұндағы Е білеушінің серпінділік қасиетін сипаттайтын коэффициент. Оны серпінділік модулі немесе Юнг модулі деп атайды. (8) формуладан
(9)
бұдан (10) Халықаралық бірліктер жүйесінде
Үйкеліс күші. Бірімен-бірі жанасқан денелердің сырғуына кедергі жасайтын күшті үйкеліс күші дейді.
Үйкелістің үш түрі бар: тыныштық үйкелісі, сырғанау үйкелісі, домалау үйкелісі.
Тыныштық үйкелісі кезінде жанасқан денелрдің бір-бірімен салыстырғандығы орын ауыстыруы болмайды.
(11)
мұндағы тыныштық үйкеліс коэффициенті, -тіректің реакция күші.
Сырғанау үйкелісі кезінде жанасқан денелердің бір-бірімен салыстырғандағы орын ауыстыруға болады.
(12)
мұндағы сырғанау үйкелісінің коэффициенті, оның мәні көптеген жанасқан денелер үшін есептелінген.
Домалау үйкелісі цилиндр, шар т.б. дөңгелек
формалы денелер мен жазық беттер арасында немесе бір-бірінің арасында болады.
(13)
мұндағы домалау үйкеліс коэффициенті, R-домалайтын дененің шеңбер радиусы.

Импульс. Импульстің сақталу заңы
Ньютонның екінші заңын пайдаланып уақыттың белгілі бір моменті үшін дененің қозғаушы күштің, массаның және үдеудің мәндерін анықтауға болады.
Массаны бастапқы жылдамдықпен қозғалағн денеге t уақыт аралығында тұрақты F күші әсер етсін. Осы күштің әсерінен дене тұрақты үдеу алады және жылдамдыққа ие болады.
Ньютонның екінші заңы бойынша:

немесе (14)
Мұндағы күш импульсі, қозғалыс мөлшері деп аталады және Р әрпімен белгіленеді. .
Денеге әсер ететін тұрақты күш импульсі, дененің импульсінің немесе қозғалыс мөлшерінің өзгерісіне тең.
Ньютонның екінші заңын дифференциялдық формуламен жазайық:
, (15)
дененің массасы тұрақты болғандықтан дифференциял белгісінің астына енгізуге болады.
(16).
Масса тұрақты болғанда (15) және (16) теңдеулері эквивалентті.
Импульс түсінігін пайдаланып, Ньюьонның екінші заңын мына түрде жазуға болады: (17) немесе .
Егер масса тұрақты болмаса онда соңғы теңдеулерден
,
екендігін ескерсек, .
Тұйықталған жүйеде дененің толық импульсі-қозғалыстың барлық уақытында тұрақты шама болады.
(18)
Бұл заңдылық импульстің сақталу заңы деп аталады. Импульстің сақталу заңы-физиканың іргелі заңдарының бірі. Ол макроденелер жүйесі үшін қалай дұрыс болса, микробөлшектер жүйесі үшін де солай дұрыс.
Жұмыс және қуат
Егер материалық нүкте тұрақты күштің әсерінен S қашықтыққа орын ауыстырса, онда күштің атқарған жұмысы
(19)
Егер болса, онда А=0, ал болса,онда
(20)
S Жұмыстың өлшем бірлігі-Джоуль (Дж)
1-сурет 1 Дж=1Н∙1м
Егер дененің қозғалыс траекторияда түзу
сызықты болмаса және денеге әсер етуші күш
тұрақты болмаса, онда жұмысты есептеу үшін
S барлық жолды ұсақ бөліктерге бөліп, әр бөлікті 2-сурет түзусызықты деп санауға болады. Сондағы істелген элементтар жұмыс .
Ал толық жұмыс осы элементар жұмыстардың қосындысына тең:
(21)
Элементар бөліктер саны шексіз артқандағы істелген жұмыс мынаған тең:
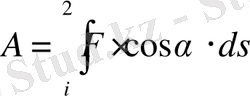(22)
Практикада жұмысты машиналар өндіреді. Жұмыстың өндірілу жылдамдығын бағалау жиі кездеседі. Сондықтан жұмыспен қатар қуат түсінігі пайдаланылады.
Қуат дегеніміз уақыт бірлігінде істелінетін жұмыс:
(23)
болғандықтан ;
болғандықтан (24)
СИ жүйесінде өлшем қуат Ваттпен өлшенеді:
1вт=107 эргс.
100 Вт=1 гвт; 1000Вт=1 квт.

Механикалық энергия
Механикада энергияның екі түрі белгілі: дене қозғалысынң жылдамдығына байланысты кинетикалық энергия, дененің тұрған орны бойынша анықталатын потенциялық энергия. Бұлардың қосындсын дененің толық механикалық энергиясы дейді.
Механикалық энергия сақталады. Осыны дәлелдеу үшін вертикаль төмен бағытта дененің еркін құлауын мысалға алайық. Дененің Һ1 биіктіктегі жылдамдығы ал Һ2 биіктіктегі жылдамдығы болсын. Осы мәндерді пайдаланыпкинематикадан белгілі мына теңдеуді жазайық

бұдан ;
Бұл өрнекті басқаша жазуға болады.
;
теңдіктің екі жағын да дененің m массасына көбейтіп мынаны табамыз:
(25)
мұндағы дененің потенциалдық, кинетикалық энергиялары.
Екі энергия мен жұмыс арсындағы байланысты қарастырайық.
Энергия кең мағынадағы түсінік. Материя қозғалысының қандай формасы болса да энергиямен өлшенеді.
Энергия дегеніміз материяның әртүрлі қозғалыс формаларының жалпы өлшеуіші. Қозғалыс формаларына механикалық (молекулалық) жылулық, электромагниттік, квантты-механикалық, ішкі ядролық қозғалыстар жатады.
Жұмыс энергия өзгерісін сандық жағынан сипаттайтын шама.
Қарапайым үдеумен қозғалатын денелердің өндіретін жұмысы кинетикалық энергияның өзгерісімен анықталады, яғни
(26)
Еркін түскен денелердің өндіретін жұмысын потенциалдық энергияның өзгеру шамасына тең:
(27)
Серпінді деформацияланған дененің потенциалдық энергиясы мынаған тең:
(28)
мұндағы Гук заңы бойынша пропорционалдық коэффициент, немесе қатаңдық ( Е-Юнг модулі, S-созылатын көлденең қимасының ауданы, х-оның бастапқы ұзындығы), деформация кезіндегі дененің ұзаруы.
Энергия арқылы қуатты анықтайтын жағдайларды қарастырайық.
Денелердің (машиналар мен қондырғылардың) энергияны өзгерту немесе ол бір түрден екіншіге түрлендіру шапшаңдығын көрсететін шаманы қуат деп атайды.
(29) (30)
Материалық нүктелер жүйесінің динамикасы
Механикада бір бірімен өзара әсерлеуші денелердің қозғалысымен айналысуға тура келдеі.Мұндайжүйелерге, мәселен, кез келген машинаның вагондарымен бірге жылулық немесе электрлік тасымалдаушына Күн мен оның планеталарын және т.б. жатқызуға болады.
Егер қозғалыс жүйені құрайтын денелердің мөлшері мен формасы ерекше бір роль атқармайтындай болса, онда материалық нүктелер жүйесінің қозғалсы жайлы қарасытырылады.
Жүйені құрайтын денелер арасында әсер ететін күштерді ішкі күштер дейді.
Жүйені құрайтын денелерге, бұл жүйеге кірмейтін басқа денелердің әсерінен болатын күштерді сыртқы күштер дейді.
Дегенмен есептің қойылу шартына байланысты, бір күштің өзі ішкі де сыртқы да болуы мүмкін. Мәселен, егер күн жүйесін біртұтас етіп қарастырсақ, онда Күн мен планеталардың өзара әсерлесу күшін ішкі, ал жеке планеталарға немесе олардың серіктеріне қатысты (мәселен Жер мен Айдың қозғалысы) күштерді қарастырсақ оларды сыртқы деп аламыз.
Массалар центрі. Механикалық жүйелер үшін массалар центрі деп аталатын түсініктің үлкен ролі бар. Элементарлы физикада денелерге әсер ететін күштердің ауырлық центрі жайлы қарастырылған. Енді ауырлық күштеріне байланыссыз, денелердің массалар центрі жайлы едәуір жалпы түсінік енгіземіз. Алдымен екі дененің массалар центрін қарастырайық.
Екі материалдық нүктенің масслар центрі дегеніміз олардың массаларына кері пропорционал болатын, өзара арақашықтығын бөлетін нүктені айтады.
Координаттары қозғалмайтын есептеу жүйесінде x,y,z, және x2,y2,z2 шамаларға сәйкес келетін, массалары m1 және m2 болатын екі екі материалдық нүкте болсын (13)-сурет. Анаметикалық геометриядан белгілі ереже бойынша кесіндіні m1,m2 берілген қатынасты бөлетін x,y,z, нүктелерінің координаттарымен келесі қатынаста байланысты.
, , (31)
Бұл теңдеулерді x,y,z координаттарына қатысты шешіп, мынаны табамыз:
; ; (32)
Енді үш материалдық нүктенің масслар
m2=2 центрін қарастырайық. Бұл да жоғарыдағы
m1=1 екі нүкте үшін табылған массалар центріне
3-сурет m3=12 ұқсас анықталады.
, ,
(33)
3-сурет бойынша:0- m1,m2 массаларының центрі
m1,m2, m3 массаларының центрі
Осы жолмен n материалдық нүктенің массалaр центрінің координаттарымен анықтауға болады.
; ; (34)
Массалар центрінің қозғалысы. Механикалық жүйенің ілгерімелі қозғалысын біртұтас қозғалысы ретінде сипаттау үшін жүйенің ауырлық центрі деп аталатын бір нүктенің қозғалысын қарастыру жеткілікті. Өйткені онда жүйеге кіретін барлық денелердің массасы жинақталған.
(34) теңдеуді мына түрде жазайық:
; ; ; (35)
Бұл теңдеуді уақыт бойынша дифференциалдайық:
;

(36)
(36) теңдеулердің сол жағында материалдық нүктенің қортқы массаның, жылдамдық мәнін беретін көбейтінділеріне тең екендігін көруге болады. Ал олардың жағында дене импульсі немесе қозғалыс мөлшері мәндері тұр, яғни:
(37)
Механикалық жүйенің толық импульсі, жүйе денелердің массасына тең және оның массалар центрінің қозғалуына сай қозғалатын материалдық нүктелердің массасының импулсіне тең. (37) теңдеуді дифференциалдап, мынаны табамыз.
(38)
жүйенің массалар центрінің импульсі, -жүйеге әсер ететін күш векторы.

Бұл импульстің сақталу заңын көрсетеді.
Реактивті қозғалыс, Мещерский мен Циолковский теңдеулері.
Табиғатта және техникада уақыттың өтуіне қарай массасы өзгеріп отыратын денелер жиі кездеседі. Мәселен планеталар массасы оларға метеориттердің құлау салдарынан артады, ол метариттердің массалары да ұшу кездерінде өзгереді.
Айнымалы массалы денелер динамикасының жалпы заңдарын И.В.Мещерский мен К.Э.Циолковский зерттеп,ашты.
T уақыт моментіндегі ракетаның массасы М, ал
Оның жылдамдығы . Уақыттың аралығында
ракетадан жылдамдықпен массасы бөлініп кетті
Z X (4-сурет).
Осыған байланысты И.В.Мещерский 1897 ж мыны формуланы қорытып шығарды.
(39)
Теңдіктің оң жағындағы F сыртқы күштердің қосындысы, оның ішінде ракетадан массаның үздіксіз бөліну салдарынан пайда болатын керек күш. Міне осы соңғы күшті реактивтік күш дейді.
Осыған ұқсас 1903 ж К.Э.Циолковский мына формуланы қорытып шығарды.
(40)
Мұндағы -ракетаның бастапқы массасы, m-оның соңғы массасы, -ракетадан бөлініп шыққан дененің жылдамдығы . Ракеталарға космостық жылдамдық беру идеясын бірінші рет К.Э.Циолковский айтты. Бұл үшін ол көп сатылы ракета жасауды ұсынды.

Қатты денелер механикасы
Қатты дененің материалдық нүктелер жүйесі ретінд. Абсолютті қатты дене.Қатты дененің ілгерімелі және айнымалы қозғалысы.
Барлық қатты денелерді көп санды материалдық нүктелер жүйесі деп қарастыруға болады. Қатты денені құрайтын бөлшектердің бір-біріне қатысты орналасуы өзгермейтін жағдайда қатты денені абсолюттік деп айтады. Мұндай қатты денелер деформацияланбайтындығы белгілі. Осы тұрғыдан алғанда абсолют қатты денелерді, реалды денелерге жақын, идеал деп санауға болады.
Қатты дененің кез келген қозғалысы қарапайым екі қозғалыс жиынтығына алып келуі мүмкін ілгерілемелі және айналмалы қозғалыстар.
Дененің және оны құрайтын бөлшектердің өздеріне қатысты парллель орны ауыстыруы кезіндегі қозғалысты ілгерілемелі қозғалыс дейді. Ілгерілемелі қозғалыс түзусызықты және қисықсызықты,бірқалыпты және бірқалырсыз болуы мүмкін. Мәселен темір жолдың түзусызқты бөлігіндегі поездың қозғалысы түзусызықты ілгерімелі қозғалысқа жатады және ол бірқалыпты үдемелі де болуы мүмкін. Осы сияқты демалыс парктеріндегі шайтан дөңгелек қозғалысы шеңбер бойымен ілгерімелі қозғалысқа жатады.
Ілгерімелі қозғалыс кезінде дененің барлық нүктелері бірдей жылдамдыққа және бірдей үдеуге ие болады.
Дененің барлық нүктелері айналу осі деп аталатын түзу бойынша шеңбер бойымен қозғалса, оны айналмалы қозғалыс дейді. Дененің айналу осі қозғалмайтын да, қозғалмалы да болуы мүмкін. Мәселен, электр қозғалтқышының роторы, қозғалмайтын ось бойыменайналады. Бір дененің өзі бір емес екі ось бойымен қозғалуы мүмкін. Мәселен О нүктесіндее орналасқан қозғалмайтын конус бетімен ОО′ ось бойымен екінші конус айналамалы қозғалысын. (6-сурет)

Сонда соңғы конус ОО′ және ОО осьтері
бойынша екі айналмаыл қозғалысқа
қатысты деуге болады. Бұлардың
нәтижесінде екі қозғалыста жалпы лездік
айналу осі бойынша жүреді.
Кез келген дене қозғалысы бір мезгілде
ілгерілемелі , айналмалы да болуы мүмкін.
Сондықтан қатты дене қозғалысының в еркіндік дәрежесі бар деп айтады. Бекітілген ось бойынша айналатын дененің еркіндік дәрежесі біреу, рельспен қозғалған дөңгелектің екі еркіндік дәрежесі бар-ілгерілемелі және айналмалы.
Қозғалмайтын ось бойынша дененің айналуы. Күш моменті.
Кез келген формадағы бір дене F күшінің әсерінен қозғалмайтын ОО′ осі бойынша айналсын. Осьтен күш түскен нүктеге дейінгі қашықтық r болсын.
Денені айналдырушы күштің М моменті деп, сол айналдырушы F күшінің күш түсетін нүктенің сызатын шеңберінің r радиусына көбейтіндісіне тең.
(1)
Бұрыннан белгілі r-күш иіні деп аталады.

Массасы ,жіпке байланған шариктің радиусы бар,
7.. шенбер бойымен қозғалысын қарастырайық. Шарик
О JO жіптің деффмациялаушы күші мен ауырлық күшінің
әсерінен қозғалады, оның алғашқысы әрқашан радиус
бойымен центрге бағытталған, ал екіншісі онымен айнымалы өзгеріп отыратын бұрыш құрады.
Шарикке әсер ететін қортқы күшпен жанама арасындағы бұрышты деп белгілейік
Шарик тангенстік күш әсерінен тангенстік үдеу алады.

Ньютонның екінші заңы бойынша;

Бұрыштық үдеу болғандықтан
(2)
(2) теңдеудің екі жағын да r-ге көбейтіп
(3)
екендігін табамыз.(3) теңдеудің сол жағындағы шама айналу центріне қатысты күш моментін береді.күш иіні деп аталады.
Инерция моменті болғандықтан,
Күш моменті (4)
Бұл теңдеуді дененің айнымалы қозғалысының негізгі теңдеуі дейді.
Формасы әртүрлі денелер үшін айналу осіне қатысты инерция мометін есептеу формулаларын бірден жазайық:
1.Ұзындығы жіңішке стержень үшін инерция моменті:

2.Ұзындығы a,ені b болатын білеушінің инерция моменті:
a
b
3.Сыртқы радиусы R,ішкі радиусы r сақинаның инерция моменті:

4.Радиусы R жұқа сақинаның инерция моменті:

5.Радиусы R дененің инерция моменті:

6.Радиусы R шардың инерция моменті:

Штейнер теоремасы
Таңдап алынған оське қатысты дененің инерция моменті берілген оське параллель және массалар центрі арқылы өтетін оське қатысты инерция моментіне дененің массасы мен екі ось арақашықтығы көбейтіндісін қосқанға тең:

Қатты дененің импульс моменті

Айналу осіне қатысты дененің импульс моменті сан жағынан осы оське қатысты оның инерция моментінің айналуының бұрыштық жылдамдығының көбейтіндісіне тең.
(5)

Айнымалы қозғалған дене динамикасының негізі теңдеуін мына түрде жазайық:
(6)
Берілген оське қатысты қатты дененің инерция моментінің шамасы тұрақты болғандықтан (6)теңдеуді мына түрде жазуға болады:
(7)
Немесе (5)теңдеуді ескеріп мына түрде жазамыз :
(8)
Бұл теңдеу моменттер импульсінің теңдеуі деп аталады.
Айналу өсіне қатысты дененің импульс моментінен алынған туынды сол оське қатысты денеге әсер етуші сыртқы күштердің моментіне тең.
Немесе басқаша
(9)
Мұндағы болған жағыдайда
(10)
Бұл-айналмалы дене импульсі моментінің сақталу заңы .

Айналатын қатты дененің кинетикалық энергиясы

Берілген бұрыштық жылдамдықпен қозғалмайтын осьтен айналатын қатты денені қарастырайық.Оны өте ұсақ элементтерге бөлейік .Сонда -ші элементтің кинетикалық энергиясы мынаған тең:
(11)
Мұндағы сол элементтің массасы ,оның сызықтық жылдамдығы .
Егер элемент центрінен айналу өсіне дейінгі қашықтық болса ондаекендігін ескеріп,бұл теңдеуді мына түрде жазамыз:
(12)
Дененің толық айналысының кинетикалық энергиясы оның жеке элементтерінің кинетикалық энергияларының қосындысына тең.
(13)
Мұндағы дененің айналу өсіне қатысты инерция моменті екендігін ескерсек :
(14)
Сонымен қозғалмайтын осьтен айналатын қатты дененің кинетикалық энергиясының формуласы материялық нүктенің кинетикалық энергиясының формуласына ұқсас,бірақ ондағы массасының инерция моменті, сызықтық жылдамдық рөлін бұрыштық жылдамдығы атқарады.
Егер дене массалар центрі арқылы өтетін оське қатысты айнала қозғалса және мұнымен қатар ілгерілемелі қозғалса онда қатты дененің толық кинетикалық энергиясы дененің массалар центрінің ілгерілемелі қозғалысының кинетикалық энергиясы мен оның айналмалы қозғалысының кинетикалық энергиясының қосындысына тең:
(15)
Ілгерілемелі және айнымалы қозғалыстар жайлы білімдерді салыстырып ,есте сақтау үшін мынадай таблицаны пайдаланайық:
Ілгерілемелі қозғалыс
Ось бойынша айнымалы қозғалыс
Нүктенің массасы m
Инерция моменті
Нүктенің орын ауыстыруы S
Бұрыштық орын ауыстыру
Нүктенің жылдамдығы

Айналудың бұрыштық жылдамдығы

Нүктенің үдеуі
Бұрыштық үдеу
Қортқы күш
Күштердің толық моменті
Импульс
Импульс моменті
Жұмыс
Жұмыс
Кинетикалық энергия
Кинетикалық энергия
Қозғалыстың негізгі теңдеуі
немесе
Қозғалыстың негізгі теңдеуі
немесе

Гироскоп
Өз өсі бойынша тез қозғалатын симметриялық денелер зырлдауық немесе гироскоп деп аталады.

A
8-сурет кардон ілмесінде орнатылған
B гироскоп

C

8-суретте кардон ілмесіне орнатылған екі сақинадан тұратын гироскоп көрсетілген.Сыртқы сақина ,ішкі сақина осьтерінің бойымен айналады.Ал гироскопының осі кардон ілмесінің ішкі сақинасына тіреліп тұрады ,сондықтан ол кез-келген бағыт бойынша бұрыла алады.Гироскопта шапшаң айналдырып жіберіп,оның тіреуін кез келген жаққа бұрғанда гироскоптың айналыс осі өзінің бағытын өзгертпей сақтайды.
Гироскоптар техникада кеңінен қолданылады.Мәселен,артқы дөңгелектері жетектеуші болып саналатын машиналарда кардондық білеу болады.
Қатты денелердің тепе-теңдігі

Еркіндік дәрежелер.Берілген денелер немесе денелер жүйесі үшін мүмкін болатын тәуелсіз қозғалысты механикада еркіндік дәреже дейді.
Берілген денелер немесе денелер жүйесі үшін бір мезгілде мүмкін болптын тәуелсіз қозғалыстар санын еркіндік дәреже саны дейді.
Мәселен,материалық нүктенің кез-келген орын ауыстыруы оның тәуелсіз үш бағыт бойынша ілгерілемелі қозғалысының нәтижесі деп қарастыруға болады.Сондықтан материалық нүктенің үш еркіндік дәрежесі бар.
Өткенде айтқанымыздай еркін қатты дененің алты еркіндік дәрежесі бар.Оның массалар центрінің ілгерілемелі қозғалысының және массалар центрі арқылы өтетін үш ось бойымен айналмалы қозғалысын сипаттау үшін біз алты теңдеу құра аламыз.Олардың үшеуі қатты дененің массалар центірінің қозғалу заңы негізінде алынған:
; ; (16)
Мұндағы күштер осьтері бойынша әсер ететін сыртқы қортқы күштер.
Басқа үш теңдеулер қатты дененің айналмалы қозғалыс динамикасы заңы негізінде алынған:
; ; (17)
Мұндағы күш моменттері осьтері бойынша сыртқы күштер моменттері.
Дене тепе-теңдікте болу үшін ,келесі алты шарт орындалуы қажет:
; ;
; ;
Тепе-теңдік орнықты және орнықсыз болуы мүмкін .

Арнайы салыстырмалық теория элементтері

Салыстырмалық принципі. Барлық есептеу жүйелерін екі топқа бөлуге болады: инерциалдық және инерциалдық емес .Берілген дене қозғалысын кинематикалық жағынан сипаттау үшін есептеу жүйесінің қайсысы болса да жарамды.Дегенмен ,есептеудің инерциалдық жүйесінде ғана дене қозғалысын сипаттау қарапайым форма алады.
Барлық инерциалдық есептеу жүйесінде барлық физикалық процестер бірдей жағыдайда өтеді.Осы тұжырымдама салыстырмалық принциптері деген атқа ие болады .Оны былай анықтауға болады:барлық инерциалдық есептеу жүйесінде физика заңдары бірдей математикалық форма алады.Бұдан,бір инерциалдық есептеу жүйесінде ашылған физикалық заңды ешқандай өзгеріссіз екінші инерциалдық есептеу жүйесінде қолдануға болатындығын көреміз.
Салыстырмалылықтың механикалық принципі, әртүрлі инерциалдық жүйелерде жүргізген тәжірибелердің нәтижесінде Галилей қортындыланды.Механиканың барлық белгілі заңдары Галилей түрлендірулерімен үйлесімді (инвариантты).Басқа жүйелер үшін бұл түрлендірулер жарамды.
Галилейдің салыстырмалық принципі қазіргі кезде былай айтылады:барлық инерциалдық есептеу жүйесінде бір механикалық құбылыс бірдей жағыдайда өтеді.
Эйнштейн пастулаттары .Лоренц түрлендірулері
1. Физикалық заңдар барлық инерциалды санақ жүйесінде бірдей,ендеше заңдардың жазылуының математикалық формасы түрлендірулерге инвариантты болуы қажет.
2. Ваккумдағы жарық жылдамдығы барлық инерциалды санақ жүйесінде бірдей және оның таралу бағытына,жарық көзі мен қабылдаушының қозғалысына тәуелсіз.
Жарық жылдамдығының тұрақтылығы Галилей түрлендіруімен келіспейді.Өйткені онда жарық бір санақ жүйесінен екіншіге ауысқан кезде өзгеріске ұшырайдыдеп көрсетілген.
Эйнштейннің бұл кеңістік пен уақыт жөніндегі бұрыннан қалыптасқан абсольюттілік жайлы түсініктерді теріске шығаруы ғылымда төңкеріс жасады деуге болады.Ол кеңістік пен уақыт қасиеттері материалдық обьектілердің қозғалуына байланысты өзгереді деп түсіндірді.
Жоғардағы екі пастулат негізінде Эйнштейн мынадай түрдегі жаңа түрлендірулер енгізді:
,

(1)

,
Мұндағы -және инерциалды санақ жүйелеріне қатысты салыстырмалы қозғалыс жылдамдығы,-вакумдағы жарық жылдамдығы,ал.
(1)теңдеуде келтірілген қатыстар галландияның атақты физигі Г.А.Лоренцтің құрметіне Лоренц түрлендірулері деп аталады.Өйткені ол бұл түрлендіруді бірінші болып алған.
Арнайы салыстырмалылық теориядағы кеңістік пен уақыт
Лоренц түрлендірулерінен шығатын кеңістік пен уақыттың кейбір маңызды ерекшеліктерін карастырайық.
Бірмезгіліктің салыстырмалылығы.Ньютон механикасында белгілі бір инерциалдық есептеу жүйесіндегі бірмезгілде болған оқиға басқа басқа инерциалдық санақ жүйесінде де бірмезгілде болады.Арнайы салыстырмалылық теорияда бұл қалай болатындығын көрейік. жылжымалы жүйесіндегіжәне нүктелерінде бір мезгілде екі оқиға болсын.Бұл оқиғалар қозғалмайтын есептеу жүйесінде уақыттың және әртүрлі моментіндегі өтеді.Жоғардағы Лоренц түрлендірулері бойынша :
，
Мұнда .
Сонымен арнайы салыстырмалылық теорияда бір есептеу жүйесінде бір мезгілде өткен екі оқиға басқа жүйеде бірмезгілде болмай қабылданады.
Оқиға ұзақтылығының салыстырмалылығы.Уақыттың баяулау эффектісі.Қозғалатын есептеу ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.