Анықталмаған және анықталған интегралдар: анықтамалар, қасиеттер және негізгі интегралдар кестесі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Жоспары:

І. Кіріспе

ІІ. Негізгі бөлім

Анықталмаған интеграл анықтамасы
Анықталмаған интегралдың қасиеттері
Анықталған интеграл анықтамасы
Анықталған интегралдың қасиеттері
Анықталған интегралды қолданып жазық фигураның ауданын табу
Негізгі интегралдар кестесі

ІІІ. Қорытынды.

ІV. Пайдаланылған әдебиеттер.

Кіріспе

Функцияның туындысы берілсе, осы функцияның өзін қалай табуға болады? Бұл механикалық тұрғыдан, материалдық нүкте қозғалысының белгілі жылдамдығы бойынша оның қозғалыс заңын табу екенін білдіреді.

Анықтама. Егер Ғ(х) функциясы ∆ аралығында дифференциалданса және

Ғꞌ(х) = f(x), V x ∆

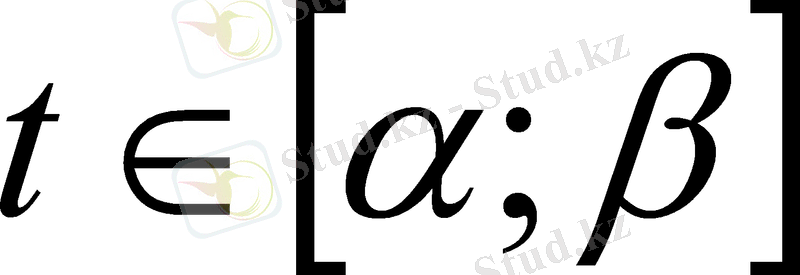Теңдігі орындалса, онда Ғ(х) функциясы f(x) функциясының ∆ аралығындағы алғашқы функциясы деп аталады.

Мысалы, f(x) = 1/2√x функциясының ∆ = (0, +∞) аралығындағы алғашқы функцияларының біреуі -Ғ(х) = √х , өйткені нүктелері үшін V x 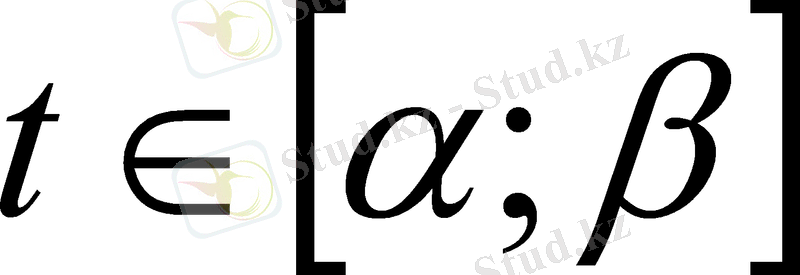(0, +∞) нүктелері үшін ( √х ) ꞌ = 1/2√x ;

Негізгі бөлім

Анықталмаған интеграл анықтамасы

f(x) = 2cos2x функциясының ∆ = (-∞, +∞) аралығындағы алғашқы функцияларының біреуі - F(x) = sin2x, өйткені V x 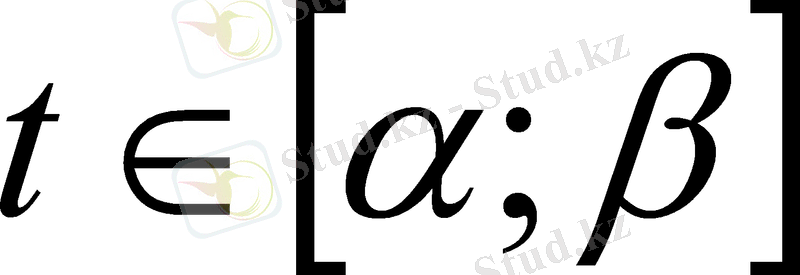( -∞ , +∞), (sin2x) ꞌ = 2cos2x.

Егер f(x) функциясының ∆ аралығындағы алғашқы функциясы F(x) болса, онда кез келген С тұрақты мен F(x) функциясының қосындысы, яғни F(x) +С функциясы да осы f(x) функциясының ∆ аралығындағы алғашқы функциясы болады, өйткені V x 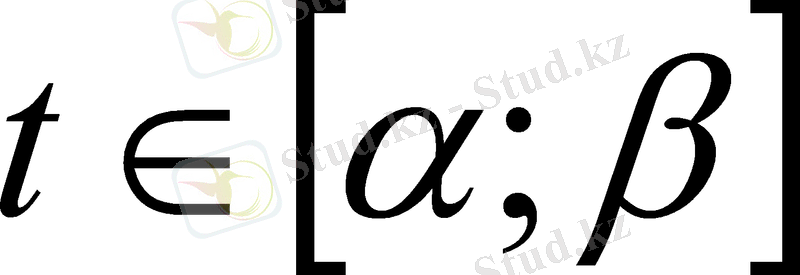∆, ( F(x) +С ) ꞌ = Ғꞌ( х ) +Cꞌ = f(x) .

Екінші жағынан, егер f(x) функциясының ∆ аралығындағы алғашқы функциялары Ғ ₁ ( х ) пен Ғ ₂ ( х ) болса: Ғꞌ ₁ ( х ) = f(x) , Ғꞌ ₂ ( х ) = f(x) , V x 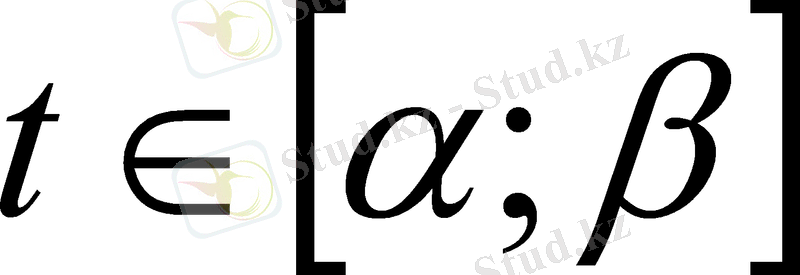∆, онда осы екі алғашқы функциялардың айырымы тұрақты С, яғни Ғ ₁ ( х ) - Ғ ₂ ( х ) =С, V x 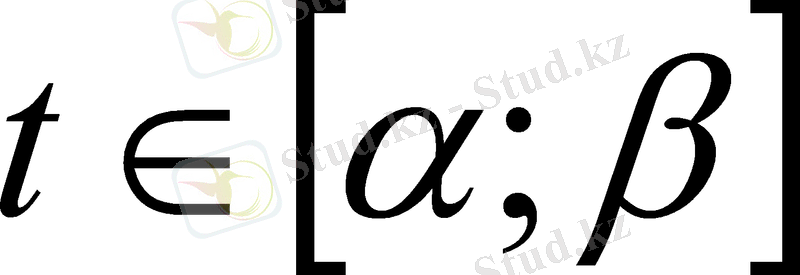∆, болатынын көруге болады. Бұл айтылғандардан, егер f(x) функциясының ∆ аралығындағы алғашқы функциясы F(x) болса, онда оның осы ∆ аралығындағы кез келген басқа алғашқы функциясы Ф (x) = F(x) +С түрінде болатыны шығады, мұндағы С осы теңдік дұрыс болатындай етіп таңдап алынатын тұрақты сан. ∆ - кез келген аралық болсын.

Анықтама. f функциясының ∆ аралығындағы барлық алғашқы функцияларының жиынтығы f функциясының ∆ аралығындағы анықталмаған интегралы деп аталады және ол ∫ f(x) dx символымен белгіленеді. Мұндағы ∫ - интеграл белгісі; f(x) - интеграл астындағы функция; f(x) dx - интеграл астындағы өрнек.

Егер, f(x) функциясының қандай да бір алғашқы функциясы F(x) болса, онда келесі теңдікті жазуға болады:

∫ f(x) dx = F(x) + C, C 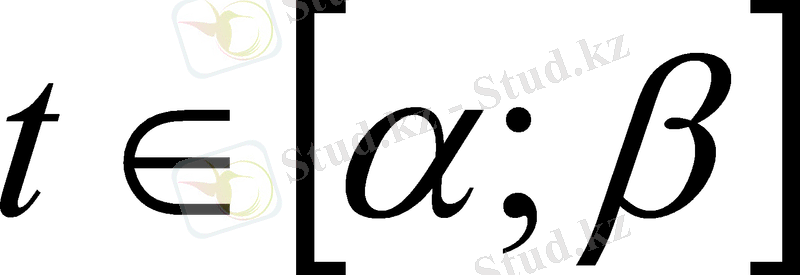R (1)

Әрине, анықтама бойынша ∫ f(x) dx ={F(x) + C} деп жазылуға тиіс, бірақ оны (1) түрінде жазу қалыптасқан.

Ескерту. ∫ f(x) dx символы f функциясының алғашқы функцияларының жиыны болғанымен, есептеу барысында олардың бірімен ғана амалдар орындалады да, есептеу аяқталған соң, жоғарыда келтірілген пайымдауларға сүйеніп, С тұрақтысын қосып жазу арқылы алғашқы функциялар жиынына көшеді.

Интеграл астындағы f функциясының dx дифференциалына көбейтіліп жазылуынан алғашқы функцияның қайсы айнымалы бойынша ізделінетінін көреміз, мысалы,

∫ x ² zdx = x ³ z/3 + C, ∫ x ² zdz = x ² z ² /2 + C

Оның басқа да ыңғайлы жақтары (интегралда айнымалы ауыстыру және т. б. ) алдымызда көрсетіледі.

f(x) функциясының алғашқы функциясын табу амалын f(x) функциясын интегралдау амалы деп атайды.

Жоғарыда, егер f(x) үшін ∆ аралығында алғашқы функция бар болса, онда ол жалғыз емес екенін көрдік. Осыған орай мынадай сұрақ туады: (a, b) аралығында кез келген f(x) функциясының алғашқы функциясы бар ма?

Кейінірек, егер f(x) функциясы (a, b) аралығында үзіліссіз немесе монотонды болса, онда f(x) үшін осы аралықта алғашқы функция бар болатынын көреміз. Қазірше кез келген үзіліссіз функцияның алғашқы функциясы бар деп қабылдап, үзіліссіз функциялармен жұмыс істейміз.

Анықталмаған интегралдың қасиеттері

Анықталмаған интегралдың қасиеттерін қарастырайық.