МЕКТЕП МАТЕМАТИКА КУРСЫНДА МАТЕМАТИКАЛЫҚ АНАЛИЗ ЭЛЕМЕНТТЕРІН ОҚЫТУ ЕРЕКШЕЛІКТЕРІ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

ӘОЖ 517.518.153:372.851
МҒТАР 27.23.17:27.29.15:14.33.09

МЕКТЕП МАТЕМАТИКА КУРСЫНДА МАТЕМАТИКАЛЫҚ АНАЛИЗ ЭЛЕМЕНТТЕРІН ОҚЫТУ ЕРЕКШЕЛІКТЕРІ
Казакбаева Гульжазира Камардиновна
Қ.А. Яссауи атындығы ХҚТУ математика кафедрасы 7М01547 тобының магистранты
Түйіндеме:
Зерттеудің алғы шарты: мектеп оқушылары арасында ұйымдастырылатын әр түрлі деңгейдегі пәндік олимпиада оқушының, мұғалімнің тіпті білім саласына қатысты барлық маманның жетістігі екені анық. Республика бойынша Түркістан облысы, оның ішінде Түркістан қаласының мектептерінде оқушылардың математикалық олимпиада жетістіктері әлі де аз. Облыстың олимпиада бойынша көрсеткіші тарихта алғашқы үштікке кірмегенін ескерсек, аталған мәселе ерекше назар аударуды талап ететінін жоққа шығаруға болмайды.
Бұл мақалада күрделі функцияның қасиеттері, туындының физикалық және геометриялық мағынасын есептер шығаруда қолдану әдістері, қолданбалы , оның ішінде әлеуметтік-экономикалық есептерді шешуде туындыны пайдаланып, тиімді шешімін табу жолдары қарастырылған.
Зерттеу барысында оқушылардың есептерді шешуін талдау педагогикалық эксперимент негізінде жүзеге асырылды, әңгімелесу әдісі арқылы есептерді шешу кезінде таңдалған математикалық әдістерді сипаттау үшін құжаттарды талдау, шешуде қолданылған алгоритмдері талқыланды.
Зерттеу нәтижесінде мектеп математика курсында математикалық анализ элементтерін зерделеу бойынша әдістемелік ұсыныстарға ерекше көңіл бөлінген, сонымен қатар 9-11-сыныпта математикадан емтиханда, олимпиадаларда кездесетін типтік математикалық есептерді шешу әдістері берілген. Әр түрлі күрделілік деңгейдегі стандартты емес және олимпиадалық есептерге оқушылармен бірге талдау жасау, шешу жолдарын көрсету бойынша ғылыми зерттеу нәтижелері берілді. Зерттеулер нәтижесінде матанализ элементтеріне байланысты стандартты емес есептерді шешудің тиімді әдісі ретінде бірнеше амал ұсынылды.
Ғылыми зерттеудің нәтижесі 10-11 сынып оқушыларын мемлекеттік емтихандар мен олимпиадаға дайындауда математика пәні мұғалімдеріне нұсқау ретінде қолданылуы мүмкіншілігі бар.
Кілт сөздер: математикалық анализ элементтері, алгебра және анализ бастамалары, туынды, тындының физикалық және геометриялық мағынасы, функцины зерттеуде туындының қолданылуы.

Кіріспе
Мектептегі математикалық білім беру мазмұнын жаңарту мәселелерімен айналысатын мамандардың назарын белгілі бір жанрдағы тапсырмалар, арнайы әдебиеттерде әртүрлі синонимдік терминдермен белгіленеді: проблемалық, шығармашылық, ізденіс, эвристикалық, яғни тапсырмалар, шешу әдісі, субъектінің қарамағында болмайтын - объективті немесе субъективті стандартты емес тапсырмалар.
Жалпы білім беретін мектепте математикалық анализ элементтерін оқытудағы қиындықтар, ең алдымен, математиканың осы саласының күрделі концептуалды аппаратымен, сонымен қатар кейбір зерттелетін анықтамалар мен теоремалардың қатаң тұжырымдары мен дәлелдемелерімен байланысты.
Дегенмен, бұл мәселені ешбір жағдайда зерттелмеген деп санауға болмайды. Керісінше, тақырып бойынша жалпылау жұмыстарының жоқтығына қарамастан, ол математиктер мен мұғалімдердің назарын барынша аударады. Бұл мәселені белгілі математиктер М.Ньютоннан бастап, П.Л. Чебышев (19 ғ.), А.Н. Колмогоров (20 ғ.) және басқа да ғалымдар зерттеген. Отандық педагог математиктер Б.Баймұханов, Е.У. Медеуов, Д.Е. Рахымбек, С. Шәкілікова және басқалардың зерттеу жұмыстарының нәтижесі елелі үлес болып саналады. Қазақ ғалымдарының ішінен О.А. Жәутіковтің математикалық анализ саласы бойынша қазақ тіліндегі іргелі зерттеу нәтижелері және оқу құралдары бар.
Математикалық анализ элементтеріне байланысты стандартты емес және олимпиадалық есептер дәстүрлі түрде мектептен тыс жұмыстардың әртүрлі нысандарында, бітірушілер үшін аттестаттау сынақтарын өткізу кезінде және мектептегі математикалық олимпиадаларда қолданылады. Сонымен қатар, кейде оқушылар ғана емес, мұғалімдер де үлгілік есептерден ерекшеленетін есептерді шешуде қиындықтарға тап болады. Бұл бір жағынан оқу орындарында математикалық пәндерді оқу процесінде және мұғалімдердің педагогикалық іс-әрекетінде осы санаттағы мәселелерді шешу тәжірибесінің жеткіліксіздігімен, сондай-ақ оларды пайдаланумен бірге жүретін объективті қиындықтардың болуы, шешуге арналған ұсыныстардың тым қысқалығы, оқу уақытының аздығы үлкен мәселеге айналып отыр[1].
Стандартты емес тапсырмалар математикалық білім берудің негізгі құрамдас бөліктерінің бірі болып табылады. Көптеген сарапшылар болашақ әлемде өмір сүру және жұмыс істеу үшін негізгі құзыреттердің өзегі стандартты емес міндеттер мен мәселелерді шешу қабілетімен келіседі[2]. Бұл тапсырмаларда оқушылар математикалық есепті шығарып, шешудің жолын, әдісін ашуы керек, өйткені олардың бұрынғы тәжірибесі есепті шығаруға мүмкіндік бермейді. Тапсырманы шешу тәртібі әдетте белгісіз және шешуші нәтижеге жету жолын көбінесе әдеттегі жолмен іздейді. Сондықтан стандартты емес тапсырмаларды шешу терең шоғырлануды, өнертабысты және уақытты қажет етеді. Әдетте дарынды оқушылармен жұмыс істеу үшін стандартты емес тапсырмаларды шешу және құру қолайлы болып саналады, өйткені тапсырмалар білімді, метатанымды және мотивацияны дамытады[4]. Дегенмен осы саладағы теориялық тұрғыда дәлелденген әдіс-тәсілдердің аздығы тақырыптың өзекті екенін айқындап отыр. Сол себепті осы тақырып бойынша зертттеу жүргізіп көру туралы шешім қабылданды.
Жұмыстың мақсаты - жоғарғы сыныптарда математикалық анализ элементтеріне байланысты стандартты емес функционалдық теңдеулерді шешу жолдарын классификациялау, мектеп оқушылары мен педагогтеріне тиімді әдістерді сипаттау.
Осы мақсатқа жетуде күрделілігі әртүрлі деңгейдегі олимпиадалық және стандартты емес есептерді іріктеп алып, шешу жолдарын көрсету маңызды.

ӘДІСТЕМЕЛІК БӨЛІМ.
Зерттеудің нысаны матанализ элементтеріне берілген стандартты емес және олимпиадалық есептерді шешу жолдары. Зерттеу Түркістан қаласындағы Ж.Ташенов атындағы №23 ІТ мектеп-лицейі базасында 10-11 сынып оқушылары арасында жүргізілді.
Ғылыми зерттеу жұмысын жүргізу кезінде, педагогикалық талдау, бақылау, бағалау, педагогикалық эксперимент әдістері қолданылды.
Мектеп курсындағы математикалық анализ элементтеріне, оның ішінде Туынды , Туындының қолданылуы тарауы бойынша стандартты емес және олимпиадалық есептерді шешудің тиімді әдістеріне дарынды оқушымен бірге талдау жүргізілді. Көрсетілген әдістерді оқушының меңгеру деңгейі бақыланды.
Педагогикалық эксперимент ретінде аталған әдістерді жекелеген оқушыларға түсіндіре отырып, берілген әдіс бойынша оқушының жетістігіне қарай тиімдісі анықталды.
Функцияның қасиеттері мен монотондылығының маңызы педагогикалық тұрғыда бағаланды.

Нәтижелерді талдау және талқылау
Математикалық анализ элементтері мектеп курсында 9-11 сынып бағдарламаларында көптеп кездеседі. Оның ішінде оқушылардың басып көпшілігі Туынды және Туындының қолданылуы тараулары бойынша қиыншылықтарға кездеседі.
Туынды тарауы бойынша мектеп оқулықтарының мазмұнын сипаттайық:
1) аргумент өсімі, функция өсімі анықтамалары енгізілді;
2) туынды ұғымына әкелетін есептер қарастырылады: физикалық (түзу сызықты қозғалыстың лездік жылдамдығын есептеу үшін), геометриялық (функция графигіне жанама туралы есеп);
3) функцияның туындысының анықтамасы енгізіліп, оны табу алгоритмі беріледі;
4) дифференциалданатын функция ұғымы, функцияның дифференциалдалуының қажетті шарты және дифференциалдау формулалары берілген. Саралау ережелері енгізіледі: қосындының туындысы, көбейтіндісі, көбейткішті туындының таңбасынан шығару. Күрделі функцияның анықтамасы беріліп, күрделі функцияның туындысын табу формуласы шығарылады;
5) екінші, үшінші және n-ші ретті туындылар туралы түсінік берілген. Екінші ретті туындының механикалық мағынасы ашылады (математиканы тереңдетіп оқытатын сыныптарда);
6) берілген нүктедегі функцияның графигіне жанаманың теңдеуі шығарылады. Функция графигіне жанаманың теңдеуін құрастыру алгоритмі зерттеледі;
7) функцияның дифференциалының, аргументтің дифференциалының түсініктері беріледі, функцияның дифференциалының көмегімен өрнектің жуық мәнін табу мәселелері қарастырылады (математиканы тереңдетіп оқытатын сыныптарда).
Базалық деңгей күрделі деңгейден формулалардың дәлелдемелері мен туындыларының жоқтығымен ерекшеленеді, негізінде барлық формулалар дайын түрде беріледі. Бірқатар оқулықтарда, негізінен, базалық деңгейде тақырып көрнекі-интуитивтік деңгейде [7,8], ал бейіндік деңгейдегі оқулықтарда формальды-логикалық деңгейде , ал бірқатар оқулықтар математикалық анализдің университет курсының бірінші бөлімдеріне жақын [3,6].
Дифференциалдық есептеудің негізгі идеясы - нүктенің жеткілікті шағын төңірегінде функцияны сызықтық түрде көрсету [9,10]. Осы идеяға сүйене отырып, біз Функцияның туындысы тақырыбын зерттеу үшін пропедевтиканың бірқатар бағыттарын бөліп аламыз:
1) сызықтық функцияны терең зерттеу, түзу сызық пен Ох осінің оң бағыты арасындағы бұрыш қалай табылатынын қайталау керек [11];
2) аргумент өсімі және функция өсімі ұғымы бойынша жұмыс, осы ұғымдардың геометриялық және механикалық түсіндірілуін және олардың өзара байланысын зерттеу; функцияның өсімшелерінің аргумент өсіміне қатынасы соңғысының функциясы екендігі туралы түсінік беру керек [11];
3) қисыққа жанама ұғымымен таныстыру, қайталау кезінде шеңберге жанаманың не екенін есте сақтау керек, дөңес функциялар мен оларға жанамаларға мысалдар келтіру керек. Мысалы, квадраттық функция y = x2, оған жанама ордината емес, абсцисса осі, дегенмен екеуінің де параболамен бір ғана қиылысу нүктесі бар [11].
Туынды ұғымының мағынасын түсіну, оның негізгі және тереңдетілген деңгейде математиканы меңгерудегі барлық оқушыларға қажеттілігін түсіндіру үшін білім алушыларға Туындының қолданылуы тарауы бойынша ғылыми-ақпараттық мәлімет беру ұсынылады.
Алгебра және математикалық талдаудың принциптері бойынша мектеп оқулықтарындағы Туындының қолданылуы тақырыбы бойынша материалдың берілуіне сипаттама берейік.
1. Орташа мән теоремалары (Ролле және Лагранж) қарастырылады (математиканы тереңдетіп оқытатын сыныптарда).
2. Функцияларды монотондылық үшін зерттеу (функцияның монотондылығының табиғаты мен оның туындысының таңбасы арасындағы байланыс). Функцияның максимум (минимум) нүктесінің анықтамасы берілген. Функцияны монотондылыққа зерттеу, экстремалды табу алгоритмдері берілген[12,16].
3. Көлденең, қиғаш және тік асимптоталар ұғымдары және оларды табу әдістері енгізіледі.
4. Ойыс (дөңес) функция мен иілу нүктесінің анықтамасы берілген (функцияның дөңес табиғаты мен оның екінші туындысының таңбасының арасындағы байланыс). Біз дөңес (ойыс) функциясын, иілу нүктесін табу алгоритмін (математиканы тереңдетіп оқытатын сыныптарда) зерттейміз.
5. Функцияны толық зерттеу және оның графигін тұрғызу алгоритмі енгізілген.
6. Үздіксіз функцияның интервалдағы ең кіші және ең үлкен мәндерін табу мәселесі және оларды табу алгоритмі қарастырылады[13,17]. Шамалардың ең үлкен және ең кіші мәндерін табуға есептер шығарылады.
Математикалық анализ элементтеріне берілген стандартты емес есептерді шешу жолдарын білім алушылармен бірге қарастыру үшін Қолданбалы есептерді шешуде туындыны қолдану тақырыбында педагогикалық эксперимент жүргізілді. Эксперимент барысында оқушылар туындыны пайдаланып қолданбалы есептерді шығаруды үйрену: функцияның сегменттегі ең үлкен және ең кіші мәндерін табу, дененің бір уақыттағы лездік жылдамдығы, дененің үдеуі, графикке жанама теңдеу. Эксперимент есептерді шешу практикумы әдісімен жүзеге асырлды. Эксперимент барысында, білім алушылармен әңгімелесу орын алды, презентация жасалды, тәжірибелік есептердің шешу жолдары қарастылырды.
Эксперимент соңында білім алушылар:
− білуі: туындының анықтамасын, туындының физикалық және геометриялық мағынасын, туындыны табу ережесін;
− істей алуы керек: туындыны табу, туындыны пайдаланып стандартты емес және олимпиадалық есептерді шығару.
Экспериментке Түркістан қаласындағы Ж.Ташенов атындағы №23 ІТ мектеп-лицейінің 10 А сыныбының оқушылары қатысты. Олардың жалпы саны 25 болатын.
Эксперимент күнделікті оқу бағдарламасына қосымша ретінде аптасына 1 рет жүргізіліп отырды.
Төменде эксперимент барысында қарастырылған мысалдар көрсетілді.
МЫСАЛ 1:

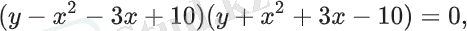
теңдеуі арқылы берілген қисық көрінетін x∈[−5;2] үшін A(5,25;−5,75) нүктесінен анықталатын бұрыштың тангенсін табыңыз[14].
Шешуі:
Суретте шеңбердің берілген нүктеден көрінетін бұрышы көрсетілген

Координаталық жазықтықта теңдеудің графигін салайық. x∈[−5;2] болғанда мына жүйені алуға болады:

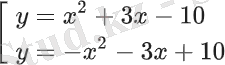
Екі теңдеудің графиктері х осін (−5;0) және (2;0) нүктелерінде қиып өтетін параболалар болып табылады. Сонымен, графикке А нүктесінен екі жанама сызып, ішкі аймақта график орналасқан осы жанамалардың арасындағы бұрыштың тангенсін табу керек.

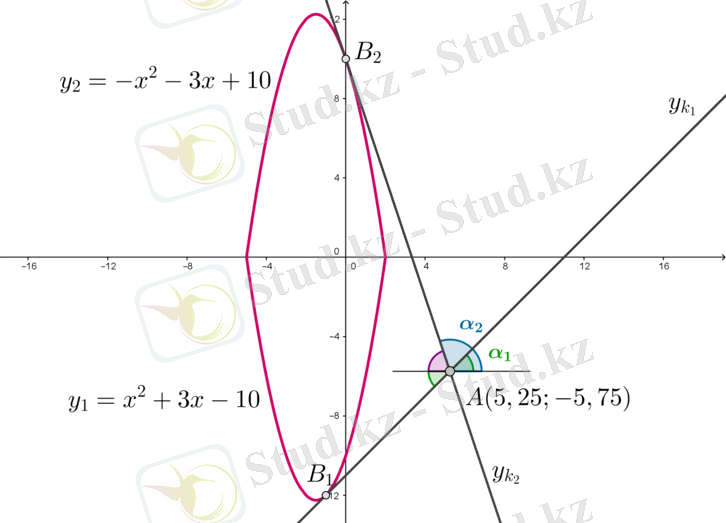
B1 нүктесінде yk1 түзуі y1-ге жанама, ал yk2 түзуі B2 нүктесінде у2 жанама болсын. Сонда абсцисса осіне параллель А нүктесі арқылы түзу жүргізілсе, онда α1 - yk1жанаманың көлбеу бұрышы, ал α2 - yk2жанамасының абсцисса осінің оң бағытына еңкею бұрышы. Сонда график орналасқан ішкі ауданындағы жанамалардың арасындағы бұрыш α1 +(180˚−α2 ) тең болады.
Жанамалардың теңдеулерін табайық.
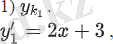сәйкесінше, егер х1 байланыс нүктесі болса, онда

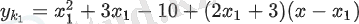
Тангенс А(5,25;−5,75) нүктесі арқылы өтетіндіктен мына теңдеуді аламыз:

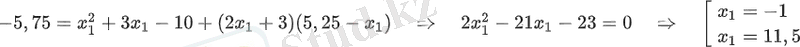
y1 графигі тек x∈[−5;2] үшін анықталғандықтан, онда х1=−1 қолайлы. Демек, жанама теңдеу келесі түрде болады:

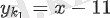
2) yk2 теңдеуін де осылай тауып аламыз:

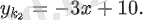
Демек, бұл дегеніміз

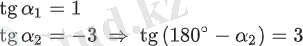
Сәйкесінше,

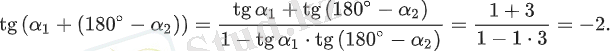
МЫСАЛ2:
Шаңғы базасы жолдың ең жақын нүктесінен 9 км қашықтықта орналасқан. Мақсат базадан аталған нүктеден 15 шақырым жерде орналасқан қалаға жетуі керек. Мақсаттың қар басқан жолда жылдамдығы 8 кмсағ, ал тегіс жолда 10 кмсағ. Қалаға баратын жолды түзу деп есептесек, қалаға қысқа мерзімде жету үшін жолдың қай нүктесіне баруы керек[15]?
Шешуі:
Есеп шарты бойынша сызба сызайық:

Белгілермен таныстырайық: В - шаңғы базасы, С - қала, L - жол, V1 - қар басқан жолдағы жылдамдық, V2 - тегіс жолдағы жылдамдық.
Тұрақтылар мен айнымалыларды белгілейік: тұрақтылар - BA, AC, V1 ,V2; айнымалылар - AD, DC, BD.
x - AD болсын, мұндағы 0 = x = 15. Пифагор теоремасын пайдаланып, BD таба аламыз.

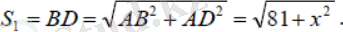
Олай болса

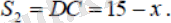
Физика курсынан қашықтықты табу формуласын еске түсіре отырып S=V∙t:
және уақытты t=St өрнектеп алайық . Сонымен Мақсат S1 жолын t1=81+x28 уақытта, ал S2 жолын t2=15-x8 уақытта жүріп өтеді.
Демек, S1 және S2 жолдарына жұмсалған уақыт :

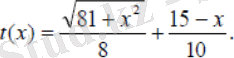
Есепте қалаға қысқа мерзімде жету үшін жол нүктесін табу қажет болғандықтан, есептің жауабын көрсету мақсатында функцияның [0, 15] кесіндісіндегі ең кіші мәнін табу керек.

Келесі кезекте кризистік нүктелерді табу керек:

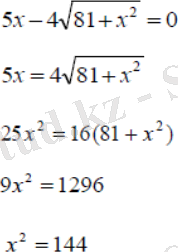
x1=12, x2=-12 есеп шартын қанағатандырмайды, өйткені берілген кесіндіге тиісті емес.
x=0, x=12, x=15 нүктелеріндегі функция мәндерін есептейік.

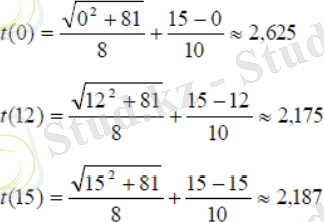
Функция x=12 нүктесінде ең кіші мәнге ие болады.
15-12=3км.
Жауап: Мақсат қалаға қысқа мерзімде жету үшін шаңғы базасынан 3 км және жолдан 12 км қашықтықтағы нүктеге баруы керек.
Зерттеу нәтижесінде келесі нәтижелер де алынды:
- жалпы білім беретін мектепте пәнаралық байланысты жүзеге асыру мәселесі бойынша ғылыми-әдістемелік әдебиеттерге талдау жасалды. Талдау осы пәндердің жалпы анықтамаларына сүйене отырып, оқу пәндері деңгейінде математика мен басқа пәндер арасындағы пәнаралық байланысты жүзеге асырудың қажеттілігі мен мүмкіндігін көрсетті.
- мектеп пәндерінен жалпы ұғымдар негізінде қоршаған дүниеге тұтас көзқарас құру, орта мектептегі пәнаралық факультативтік сабақтардың ерекшеліктері көрсетіледі, олар оқушылардың әртүрлі пәндерді оқуда алған білімдерін жалпылау мен жүйелеуден тұрады.
- осы пәндер бойынша білім алушылардың туынды туралы білімдерін тереңдету үшін пәнаралық байланысты жүзеге асыруға бағытталған Туынды және оның қолданылуы элективті курсын өткізу әдістемесі әзірленді. Бұл материал мұғалімдерге және дарынды оқушыларға, сыныптан тыс жұмыстарға, математикалық олимпиадаларға дайындыққа және т.б. көмекші бола алады.

ҚОРЫТЫНДЫ

Бұл мақала 10-11 сыныптарда математикалық анализ элементтеріне байланысты стандартты емес және олимпиадалық есептерді шешу жолдарын қарастыруға бағытталған.
Бұл жұмыста ұсынылып отырған материал білім алушыларға қызықты әрі қажетсіз қиындықтардан шығатын жол болатындай етіп жоспарланған, жоғарыда атап өткендей, туынды күрделі мәселелерді зерттеудің ең қуатты құралдарының бірі болып табылады.
Әртүрлі құбылыстарды математикалық тұрғыдан зерттеу қабілеті туындыны зерттеуді қалыптастырады. Жалпы білім беретін мектеп түлегі туынды туралы түсінікке ие болу керек, сонымен қатар оны функцияларды зерттеуге қолдануы керек. Бірыңғай мемлекеттік емтихандарда, олимпиадаларда туындыны қолдануға байланысты тапсырмалар көптеп кездеседі. Нәтижесінде Туынды тақырыбы бойынша білім алушылардың білім, білік және дағдыларын тереңдету мен кеңейтудің негізгі бағыттары анықтадлды, Туынды және оның қолданылуы тақырыбы бойынша таңдау курсы әзірленді, ол келесі мәселелерді шешуге мүмкіндік береді:
- стандартты емес есептерді шешуде білім мен дағдыларды тереңдету және кеңейту арқылы білім алушылардың теориялық дайындық деңгейін арттыру;
- оқушылардың математикалық қабілеттерін дамытып, математикаға тұрақты қызығушылықтарын қалыптастыру арқылы олардың шығармашылық әлеуетін арттыру.
Әзірленген таңдау курсын математиканы тереңдетіп оқытатын мектепте, лицейде немесе гимназияда, сондай-ақ оқу орындарында, оқу практикасында аудиторияда және факультативтік сабақтарда, дарынды оқушылармен жұмыс кезінде, оқушыларды олимпиадаға дайындау кезінде мұғалімдерге оқу-әдістемелік құрал ретінде пайдалануға болады. Сонымен қатар білім алушылар оны анықтамалық материал ретінде пайдалана алады.

(ГОСТ 7.1-2003 БОЙЫНША)
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Бөрібекова Ф. Б., Жанатбекова Н. Ж. Қазіргі заманғы педагогикалық технологиялар: Оқулық. - Алматы: 2014. - 39 бет.
2. Бөрібекова Ф. Б., Жанатбекова Н. Ж. Қазіргі заманғы педагогикалық технологиялар: Оқулық. - Алматы: 2014. - 61 бет.
3. Жәутіков О.А. Математикалық анализ курсы (оқулық). Алматы: -Экономик , 2014. -144 бет
4. Блох А.Я., Гусев В.А., Дорофеев Г.В. Методика преподавания математики в средней школе: частная методика : учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. - М.: Просвещение, 1987. - 416 с.
5. Гусев В. А., Силаев Е. В. Методические основы дифференциации обучения математики в средней школе. -М.: Принт, 1996. - 131 с.
6. Клякля М. Формирование творческой математической деятельности учащихся в классах с углубленным изучением математики в школах Польши : дис. ... ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.