Екі еселі интегралдарды есептеу: декарттық және полярлық координаталар, Якобиан және қолданбалар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

https://youtu. be/Qx45IL1Eut4 Екі еселі интегралдарды есептеу

7. 2 ЕКІ ЕСЕЛІ ИНТЕГРАЛДЫ ЕСЕПТЕУ

7. 7. 1 Екі еселі интегралды декарттық координаталар жүйесінде есептеу

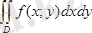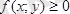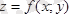Екі еселі интегралды есептеу ол біртіндеп екі анықталған интегралды есептеуге келтірілетінін көрсетеміз. $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image001.png$ екі еселін интегралын есептеу керек болсын, мұндағы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image002.png$ функциясы D облысында үзіліссіз функция болсын, онда ол екі еселі интеграл жоғары жағынан $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image003.png$ бетімен шектелген цилиндрлік дененің көлемін өрнектейді. Параллельдік қималар әдісін қолданып, осы көлемді табайық. Жоғарыда

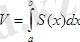
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image004.png$

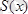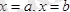екенін көрсеттік. Мұндағы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image005.png$ Ох осіне перпендикуляр жазықтық қимасының ауданы, $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image006.png$ жазықтықтардың теңдеуі.

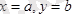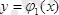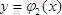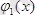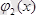D облысы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image007.png$ түзулерімен және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image008.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image009.png$ қисықтарымен шектелген қисық сызықты трапеция болсын, $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image010.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image011.png$ функциялары 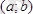$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image012.png$ кесіндісінде үзіліссіз және барлық 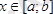$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image013.png$ үшін $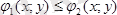Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image014.png$ .

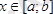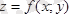Мұндай облысты Оу осінің бағытымен дұрыс облыс деп атайды. Оу осіне параллель кез келген түзу облыс шекараларын екі нүктеде қиып өтеді. Ох осіне перпендикуляр цилиндрлік денені жазықтықпен қиғандағы қиманы салайық: $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image016.png$ , мұндағы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image013.png$ . 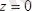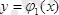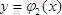Қимадан $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image003.png$ , $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image017.png$ , $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image008.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image009.png$ сызықтармен шектелген АВСD қисық сызықты трапециясын аламыз.

Бұл трапецияның 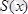$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image018.png$ ауданын

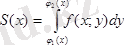
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image019.png$

анықталған интегралы көмегімен табамыз.

Параллель қималар әдісі бойынша іздеп отырған цилиндрлік дененің көлемі төмендегі түрде анықталады:

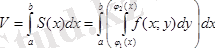
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image020.png$

Сондықтан

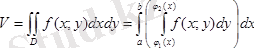
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image021.png$

Бұл теңдікті төмендегі түрде жазуға болады

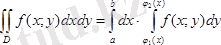
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image022.png$

(7. 1)

формуласы екі еселі интегралды декарттық координаталар системасында есептеу формуласы.

(7. 1) формуласының оң бөлігін D облысы бойынша 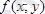$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image023.png$ функциясының екі еселі интегралы деп атайды. 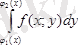$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image024.png$ интегралын ішкі интегралы деп атайды.

Екі еселі интегралды интегралдау үшін ең алдымен ішкі интегралды аламыз, х-ті тұрақты деп аламыз. Содан кейін сыртқы интегралды есептейміз, яғни бірінші интегралдан шыққан нәтижені шектері а -дан b -ға дейін х бойынша интегралдаймыз.

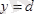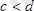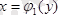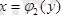Егер D облысы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image025.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image026.png$ ( $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image027.png$ ) түзулерімен $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image028.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image029.png$ қисықтарымен шектелсе, барлық 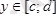$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image030.png$ үшін $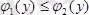Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image031.png$ болса, яғни D облысы - Ох осі бағытымен дұрыс облыс болса,

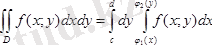
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image032.png$

(7. 2)

мұнда ішкі интегралды есептегенде у -ті тұрақты деп саналады.

7. 7. 2 Екі еселі интегралды полярлық координаталар системасында есептеу

Екі еселі интегралды есептеуді жеңілдету үшін көп ретте оның айнымалыларын ауыстыру амалын қолданады. Тәуелсіз х және у айнымалыларының түрлендіруін анықтайық:

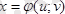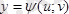$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image033.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image034.png$ .

(7. 3)

Егер (7. 3) функциясының белгілі бір D облысының $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image035.png$ жазықтығында бірінші ретті үзіліссіз дербес туындылары бар болса және

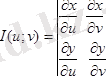$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image036.png$ ,

(7. 4)

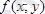анықтауышы нөлге тең болмаса, ал $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image023.png$ функциясы D облысында үзіліссіз болса, онда екі еселі интегралға төмендегідей айнымалыларын ауыстыру амалын қолдануға болады:

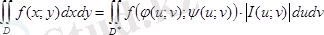
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image037.png$

(7. 5)

(7. 4) функционалдық анықтауышын Якобиан анықтауышы деп атайды. (7. 7. 5) формуласы дәлелдемесіз келтіріледі.

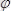Дербес жағдайда екі еселі интегралды есептеуде х және у декарттық координатасын $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image038.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image039.png$ полярлық координатаға ауыстыруы қолданылады. 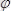$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image040.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image041.png$ ретінде $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image038.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image039.png$ полярлық координаталарын аламыз. Олар декарттық координата мен 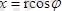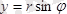$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image042.png$ , $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image043.png$ формуласымен байланысады. Осы теңдіктің оң бөлігі - үзіліссіз дифференциалданатын функциялар. (7. 4) теңдеуден Якобион анықтауышы

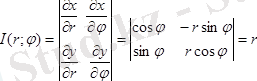
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image044.png$

(7. 5) теңдеуінен айнымалыларын ауыстыру формуласы төмендегідей болады:

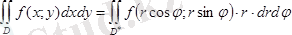
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image045.png$

(7. 6)

мұндағы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image046.png$ облысы декарттық координаталар жүйесіндегі D облысына сәйкес полярлық координаталар системасының облысы.

Еселі интегралды полярлық координатада есеп үшін еселі интегралды есептеу ережелері қолданылады. $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image046.png$ облысы. (7. 6) формуласын төмендегі түрде жазуға болады:

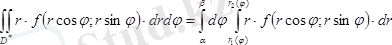
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image053.png$

(7. 7)

Ішкі интегралды есептегенде 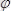$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image039.png$ тұрақты ретінде алынады.

Ескерту.

1. Интеграл астындағы функция 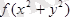$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image055.png$ түрінде, ал D облысы шеңбері, сақина болғанда полярлық координатаға көшу арқылы есептеген ыңғайлы.

7. Практикада еселі интегралды есептегенде 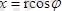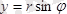$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image042.png$ , $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image043.png$ ауыстырулары арқылы полярлық координатаға көшеді, сондай-ақ D облысы да полярлық координаталарға түрлендіріледі. 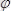D облысын $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image046.png$ облысына түрлендірілуі болмайды, полярлық координата мен декарттық координаталарды байланыстырып керекті интегралдау шектерін $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image038.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image039.png$ бойынша алынады.

7. 7. 3 Екі еселі интегралдың қолданылуы

Екі еселі интегралдың қолданылуының кейбір мысалдарын көрсетейік.

Дене көлемі

Цилиндрлік дененің көлемі

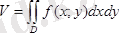
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image057.png$

формуласымен анықталады, мұндағы 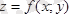$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image003.png$ - денені жоғарыдан шектеген беттің теңдеуі.

Жазық фигураның ауданы

Егер (7. 4) формуласындағы 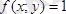$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image058.png$ деп алсақ, онда цилиндрлік дене биіктігі $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image059.png$ болатын цилиндрге айналады. Мұндай цилиндрдің көлемі, бізге белгілі D табанының ауданының сандық мәніне тең. Сонда D облысының S ауданының сандық мәніне тең. Сонда D облысының S ауданының есептеу формуласын аламыз:

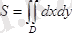
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image060.png$

немесе полярлық координатада

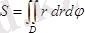
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image061.png$

Жазық фигураның ауданы

Жоғарыда көрсетілген айнымалы тығыздығы 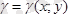$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image062.png$ болатын D жазық пластинкасының массасы

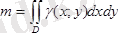
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image063.png$

Жазық финураның ауырлық центрімен статикалық моменттері

D фигурасының Ох және Оу осьтеріне қарағанда статикалық моменттері төмендегі формулалар арқылы есептелуі:

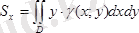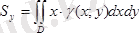
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image064.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image065.png$

ал фигура массасының ауырлық центрінің координаталары

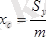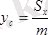$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image066.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image067.png$ .

Жазық фигураның инерциялық моменті

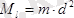Массасы $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image068.png$ материалдық нүктенің l осіне қарағандағы инерциялық моменті сол нүктенің осьтен қашықтығы d -ның квадратына оның массасын көбейткенге тең, яғни $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image069.png$ . Жазық фигураның Ох және Оу осьтеріне қарағандағы инерциялық моменттері

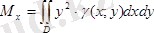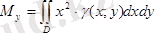
$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image070.png$ және $Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image071.png$

формулалары арқылы есептелінеді. Ал координталар бас нүктесіне қарағандағы инерциялық момент 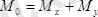$Описание: E:\ЭУИ\мат.анализ\Teory\tema7.2.files\image072.png$ формуласымен есептелінеді.