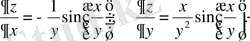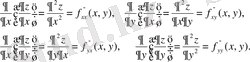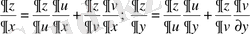Көп айнымалылы функциялар: анықталуы, дербес және толық туындылары, бағыттық туындылары мен көп еселі интегралдар
1-дәріс. Көп айнымалылы функция
Көп айнымалылы функцияның анықталу облысы
Ссылка: https://www. youtube. com/watch?v=tn43tI4KRhI
Егер
D
облысында бір-бірінен тәуелсіз қос (
\[x,y\]
) айнымалыларының әрбір мәніне
z
айнымалысының анықталған бір мәні сәйкес келсе, онда
z
айнымалысы х және у айнымалыларына байланысты екі айнымалы функция деп аталады және оны
\[z\not\lbrack\widehat\Pi\widehat\Pi\widehat\Pi\widehat\Sigma\widehat\Sigma\circ\widehat\Sigma\]
,
\[z\not=F^{\prime}(\chi_{},\,y)\]
және тағы да басқа симводардың (ишараттардың) бірімен белгілейді.
х
және
у
мәндерінің қос
(
\[x,y\]
)
жиынын осы функцияның анықталу облысы деп атайды.
\[I{\tilde{\sigma}}\bar{\theta}\]
жазықтығы,
\[I{\tilde{\sigma}}{\mathcal{G}}\]
жазықтығының тұйық сызықтармен шектелген бөлігі немесе осы жазықтықтың бірнеше бөліктерінің жиынтығы болады.
\[I{\tilde{\sigma}}\bar{\sigma}\]
тік бұрышты координаттар жүйесіндегі геометриялық бейнесі (графигі) осы теңдеумен анықталатын бет болып табылады.
Егер бір-бірінен тәуелсіз
\[{\mathcal{X}}_{1},{\mathcal{X}}_{2},\ast\ast,{\mathcal{X}}_{n}\]
айнымалыларының әрбір мәніне
u
айнымалысының анықталған бір мәні сәйкес келсе, онда
u
айнымалысы
\[{\mathcal{X}}_{1},{\mathcal{X}}_{2},\ast\ast,{\mathcal{X}}_{n}\]
айнымалыларына байланысты көп айнымалы функция деп аталады да
\[\begin{array}{c c c}{{u={\cal M}(\chi_{1},\chi_{2},\ldots,\chi_{n}),}}&{{~~u=f(\chi_{1},\chi_{2},\ldots,\chi_{n})}}\end{array}\]
,
символдарымен белгіленеді.
1-мысал.
\[\scriptstyle z\;=\;x^{2}\,+\,y^{3}\]
функциясының анықталу облысын табу керек.
Шешуі. Берілген функция
х
пен
у
-тің кез келген мәнінде анықталған, яғни анықталу облысы бүкіл
\[I{\tilde{\sigma}}{\mathcal{G}}\]
жазықтығы болып табылады.
2 - мысал.
\[z\rfloor\mathrm{H}(\lambda x-\Theta)\]
функциясының анықталу облысын табу керек.
Шешуі. Логарифмдік функция
\[2.{\widetilde{o}}-\ \emptyset>0\]
,
яғни
\[{\bar{\vartheta}}<2x\]
болғанда ғана анықталады. Осыдан функцияның анықталу облысы
\[2\tilde{\sigma}-\;\mathcal{G}=0\]
түзуінен төмен орналасқан
\[I{\tilde{\sigma}}\bar{\sigma}\]
жазықтығының бөлігі болып табылады.
3-мысал.
\[z=\sqrt{\tilde{\sigma}^{2}+\theta^{2}-\dot{\alpha}^{2}}\]
функциясының анықталу облысын табу керек.
Шешуі. Функция нақты мәндерін
\[\tilde{O}^{2}\,+\,O^{2}\,-\,\tilde{d}^{2}\,\,\,\Sigma(\cal{)}\]
немесе
\[{\tilde{\sigma}}^{2}+\theta^{2}\ \geq{\tilde{a}}^{2}\]
болғанда ғана қабылдайды, яғни функцияның анықталу облысы центрі координаталар жүйесінің бас нүктесі, ал радиусы
а
-ға тең болатын дөңгелектен тыс орналасқан
\[I{\tilde{\sigma}}{\mathcal{G}}\]
жазықтығының бөлігі.
Көп айнымалы функцияның үзілісіздігі
Алдымен берілген нүктенің аймағы туралы түсінік берейік.
\[\begin{array}{c c}{{\tilde{I}}}&{{0}}\\ {{0}}&{{0}}\end{array}\]
нүктесінің
\[{\hat{\mathcal{J}}}^{\Phi}\]
радиусты аймағы деп
\[{\sqrt{({\hat{\theta}}\cdot{\tilde{\sigma}}_{0})^{2}+(\delta\cdot\,{\tilde{\sigma}}_{0})^{2}}}
қанағаттандыратын барлық
\[\bar{I}\setminus(x,y)\]
нүктелерінің жиынтығын айтады, яғни орталығы
\[\begin{array}{c c}{{\tilde{I}}}&{{\;0}}\end{array}(\mathcal{X}_{0},\;\mathcal{Y}_{0})\]
нүктесі болатын, радиусы
\[{\boldsymbol{r}}-\]
ге тең дөңгелектің ішінде жататын барлық нүктелер жиынын айтады.
Қандайда бір
\[\bar{\boldsymbol{D}}\]
обласында анықталған
функциясы және
\[\bar{\boldsymbol{D}}\]
обласына тиісті
\[\begin{array}{c c}{{\hat{I}}}&{{}}\\ {{0}}&{{0}}\end{array}\]
нүктесі берілсін.
Егер кезкелген
\[\scriptstyle e\;>0\]
оң саны үшін,
\[r>0\]
саны табылып, барлық
\[{\hat{I}}\setminus(x,y)\]
нүктелері үшін
\[\begin{array}{c}{{\dot{I}\ \ _{0}\dot{I}\ \ |=\sqrt{(\bar{\theta}\cdot\bar{\theta}_{0})^{2}+(\theta-\ \bar{\theta}_{0})^{2}}
теңсіздігі орындалғанда,
\[\left|f(x,y)-\ A\right|<\varepsilon\]
теңсіздігі орындалса, онда
\[\mathbf{\nabla}\lambda\]
санын
\[z\longrightarrow\beta(x,\,y)\]
функциясының
\[{\hat{I}}\setminus(x,y)\]
нүктесі
\[\operatorname*{lim}_{x\to x_{0}}f(x,y)=A.\]
\[\begin{array}{c c}{{\hat{I}}}&{{}}\\ {{0}}&{{0}}\end{array}\]
нүктесі
\[z\longrightarrow\beta(x,\,y)\]
функциясының анықталу облысына тиісті болсын. Егер
\[\operatorname*{lim}_{x\oplus x_{0}}f(x,y)=f(x_{0},{\bf y}_{0})\]
(5. 1)
теңдігі орындалса, онда
\[z\not\lbrack\mathcal{f}(\chi_{\scriptscriptstyle\scriptscriptstyle J})\]
функциясы
\[\begin{array}{c c}{{\hat{I}}}&{{}}\\ {{0}}&{{0}}\end{array}\]
нүктесінде үзіліссіз дейді.
\[\bar{\boldsymbol{D}}\]
обласының әрбір нүктесінде
\[z\longrightarrow\beta(x,\,y)\]
функциясы үзіліссіз болса, онда
\[z\longrightarrow\beta(x,\,y)\]
функциясы
\[\bar{\boldsymbol{D}}\]
обласында үзіліссіз деп аталады.
Егер қандайда бір
\[\begin{array}{c c}{{\tilde{I}}}&{{\downarrow}}\\ {{\downarrow}}&{{\downarrow}}\end{array}\quad\quad\]
нүктесінде (5. 1) шарты орындалмаса, онда
функциясы
\[\begin{array}{c c}{{\tilde{I}}}&{{\downarrow}}\\ {{\downarrow}}&{{\downarrow}}\end{array}\quad\quad\]
нүктесінде үзілісті дейді.
Көп айнымалылы функцияның дербес туындылары
\[I{\tilde{\sigma}}{\mathcal{G}}\]
жазықтығының
D
обылысында анықталған
\[z\not\lbrack\mathcal{f}(\chi_{\scriptscriptstyle\scriptscriptstyle J})\]
функциясын қарастырайық. Мұндағы
х
пен
у
-ті бекітіп алып,
х
айнымалысына
\[\Delta\vec{\sigma}\]
өсімшесін берейік. Сонда
х
айнымалысы бойынша
z
функциясының
\[\Delta_{x}z\]
дербес өсімшесі
\[\mathbf{D}_{x}z=f(x+\mathbf{D}x,y)-f(x,y)\]
формуласымен анықталады.
\[z\longrightarrow\beta(x,\,y)\]
функциясындағы
х
пен
у
айнымалыларын бекітіп алып,
у
айнымалысына
\[\Delta{\tilde{G}}\]
өсімшесін берсек, онда
у
айнымалысы бойынша дербес өсімшесі
\[\mathrm{D}_{\theta^{Z}}=f(x,\vartheta+\mathrm{D}y)-f(x,y)\]
формуласымен анықталады.
\[z\not\lbrack\mathcal{f}(\chi_{\scriptscriptstyle\scriptscriptstyle J})\]
функциясының
х айнымалысы бойынша дербес туындысы
деп
шегін айтады.
\[z\longrightarrow\beta(x,y)\]
функциясының
х
айнымалысы бойынша дербес туындысын есептеу үшін
\[\overset{P}{\underset{\sim}{\sqrt{}}}\]
функциясының
у
- тұрақты деп алғандағы х бойынша туындысын есептеу керек.
у айнымалысы бойынша дербес туындысы
деп
\[\operatorname*{lim}_{\lambda\cos0}{\frac{{\bf{D}}_{\delta}z}{{\bf{D}}}}=\operatorname*{lim}_{\mathrm{{\scriptsize{D}}}\rightarrow0}{\frac{f(x,y+{\bf{D}}y)_{-}\ f(x,y)}{{\bf{D}}\theta}}=\frac{\P_{\lbrack Z}}{\P\lbrack{\cal{D}}}=f_{\delta}^{'}(x,y)\]
шегін айтады.
\[z\longrightarrow\beta(x,y)\]
функциясының
у
айнымалысы бойынша дербес туындысын есептеу үшін
\[\stackrel{\cal P}{\longrightarrow}_{\infty}\]
функциясының
х
- тұрақты деп алғандағы
y
бойынша туындысын есептеу керек
5. 4-мысал.
\[z=x^{2}+2y^{2}-\,3x y-\,5x+6y+4\]
функцияның дербес туындысын табу керек.
Шешуі:
у
-ті тұрақты деп алып,
\[{\frac{\mathbb{C}[z}{\mathbb{I}]x}}=2x-\,3y-5\]
табамыз.
Осы сияқты,
х
-ті тұрақты деп алып,
\[\frac{\vert z}{\vert\bar{\theta}\bar{\theta}}=4.6-3\bar{\theta}+6\]
табамыз.
5-мысал.
\[z=a\mathrm{r}\mathrm{cs}^{*}\mathrm{l}\mathrm{l}(x y^{2})\]
функциясының дербес туындыларын табу керек.
Шешуі:
\[{\frac{\P z}{\ \|x}}={\frac{y^{2}}{\sqrt{1-x^{2}y^{4}}}},\]
\[{\frac{\|z}{\|_{y}}}={\frac{2x y}{\sqrt{1-x^{2}y^{4}}}}.\]
6-мысал. Үш айнымалы
Шешуі:
\[{\frac{\vert\vec{v}\vert}{\vert x}}=\bigl(3x^{2}+\theta^{2}\bigr)\mathrm{e}^{2}\cdot e^{x^{3}+\vec{v}y^{2}},\]
\[\frac{\P(u}{\P y}=2\,\tilde{\sigma}y z^{2}\cdot e^{x^{3}+\theta y^{2}},\]
\[{\frac{\|u}{\|_{Z}}}=2z\cdot e^{x^{3}+\vec{\sigma}y^{2}}.\]
4 Көп айнымалылы функцияның толық өсімшесі мен толық дифференциалы
Егер
х
пен
у
айнымалылары бекітіліп алынып, олар сәйкесінше
\[\Delta\vec{\sigma}\]
және
\[\Delta{\tilde{G}}\]
өсімшілерін қабылдаса, онда
z
функциясының толық өсімшесі
\[\mathrm{D}\zeta=f(x+\mathrm{D}{\bar{\vartheta}},y+\mathrm{D}\vartheta)-f(x,y)\]
формуласымен анықталады.
\[z\longrightarrow\bar{f}(x_{,}\,y)\]
функциясының
\[\bar{I}\setminus(x,y)\]
нүктесінде дербес туындылары бар болсын, онда
\[\Delta z\]
толық өсімшесіні дербес туындылары арқылы
\[\mathrm{D}z={\frac{\P[f\bigl(\tilde{\sigma},\,\sigma\bigr)}{\P[x}}\mathrm{D}\tilde{\sigma}+{\frac{\P[f\bigl(\tilde{\sigma},\,\sigma\bigr)}{\P[\theta}}\mathrm{D}\theta+a_{1}\Omega\tilde{\sigma}+a_{2}\Delta\tilde{\sigma}\]
түрінде жазылады, мұндағы алдыңғы екі қосынды өсімшенің
негізгі бөлігі
, ал кейінгі екі қосынды
қосалқы бөлігі
деп аталады.
\[\Delta\vec{\sigma}\]
және
\[\Delta{\tilde{G}}\]
шамаларымен салыстырғанда қосалқы бөлігі жоғары ретті шексіз аз шама болғандықтан
\[\mathrm{D}r={\sqrt{(\mathrm{D}x)^{2}+(\mathrm{D}y)^{2}}}\to0\]
ұмтылғанда
\[a_{1}\mathrm{D}x+a_{2}\mathrm{D}y\to0\]
.
Толық өсімшенің негізгі бөлігі
функцияның толық дифференциалы
деп аталып,
\[d z={\frac{\P z}{\P x}}\,d x+{\frac{\P z}{\P G}}\,d y=f_{x}\langle x,y\rangle d x+f_{y}^{\prime}(x,y)d y\]
деп белгіленеді. Мұндағы
\[d x=\operatorname{D}x,d y=\Delta y\]
.
Егер
\[u=f(x,y,z,*,t)\]
көп айнымалылы функциясы берілсе, онда оның толық дифференциалы
\[d u={\frac{\P u}{\P[x}}d x+{\frac{\P u}{\P\flat}}d y+{\frac{\P u}{\P z}}d z+...+{\frac{\P u}{\partial t}}d t\]
7-мысал.
\[z=x^{2}+x y^{2}+\mathrm{sin}\,y\]
функциясының толық дифференциалын табу керек.
Шешуі.
\[{\frac{\|z}{\|x}}=2x+y^{2},\ {\frac{\|z}{\|y}}=2x y+\cos y.\]
\[d u={\frac{\P u}{\P x}}d x+{\frac{\P u}{\P y}}d y=(2x+y^{2})d x+(2x y+\cos y)d y.\]
8-мысал.
\[u=\left|\operatorname{m}(x^{2}+2y^{2}+3z^{2})\right.\]
функциясының толық дифференциалын табу керек.
Шешуі.
\[{\frac{\P u}{\P|x}}={\frac{2x}{x^{2}+y^{2}+z^{2}}};\;{\frac{\P u}{\P|y}}={\frac{4y}{x^{2}+y^{2}+z^{2}}};\;{\frac{\P[u}{\P z}}={\frac{6z}{x^{2}+y^{2}+z^{2}}}.\]
\[d u={\frac{\P u}{\P\!\!\|x}}d x+{\frac{\P u}{\P\!\!\|y}}d y+{\frac{\P u}{\P\!\!\|z}}d z={\frac{2x d x+4y d y+6z d z}{x^{2}+y^{2}+z^{2}}}.\]
\[\mathrm{D}r={\sqrt{(\mathrm{D}x)^{2}+(\Delta y)^{2}}}\]
аз мәнінде дифференцианалданатын
\[z\longrightarrow\beta(x,y)\]
функциясы үшін
\[\mathrm{D}z\ \approx d z\]
жуықтап есептеу формуласы қолданылады, осыдан
\[f(x+\mathrm{D}x,y+\mathrm{D}y)\sim f(x,y)+d z=f(x,y)+{\frac{\P f(x,y)}{\P|x}}\mathrm{D}x+{\frac{\P f(x,y)}{\P y}}\Delta y.\]
9-мысал.
\[\sqrt{4.03^{2}+2.98^{2}}\]
санының жуық мәнін табу керек.
Шешуі.
\[{\mathcal{L}}={\sqrt{x^{2}+y^{2}}}\]
функциясын қарастырайық.
\[x+\mathrm{D}x=4,03\]
осыдан
\[{\mathcal{X}}\not=\Omega_{\mathsf{\operatorname{\scriptsize{J}}}}\ \mathbb{L}{\mathcal{X}}\mathbb{-}\left(\right)_{\mathsf{\mathrm{\scriptsize{J}}}}\langle\!\mathord{\mathcal{Z}}\rangle_{\mathsf{\mathbf{\omega}}}\]
\[y+\mathrm{D}y=2.98\]
осыдан
\[y=3,\ \mathrm{D}y=-0,02;\]
\[z=\sqrt{4^{2}+3^{2}}=5,\,\frac{\P z}{\P x}=\frac{x}{\sqrt{x^{2}+y^{2}}}=\frac{4}{5},\,\frac{\P[z}{\P y}=\frac{y}{\sqrt{x^{2}+y^{2}}}=\frac{3}{5},\]
\[\sqrt{4,03^{2}+2,98^{2}}\sim z+\frac{9|z}{\P x}{\bf D}x+\frac{9|z}{\P y}{\bf D}y=5+\frac{4}{5}\Re{,}0{,}0{,}0{,}2=5+\bar{5}{\mid}=5,012.\]
Жаттығулар
Берілген функциялардың анықталу облысын табу керек.
1.
\[z=\sqrt{a^{2}\,-\,x^{2}-y^{2}}.\]
Жауабы:
\[x^{2}+y^{2}\leq a^{2}-\]
центрі
\[O(0;0),\]
ал радиусы
а
болатын шеңберімен шектелген
\[I{\tilde{\sigma}}\delta\]
жазықтығының бөлігі.
2.
\[z\simeq\sum\chi+\Im y_{*}\]
Жауабы: Бүкіл
\[\textstyle{O x y}\]
жазықтығы.
3.
\[z=\vert\mathrm{m}(x+y).\]
Жауабы:
\[y\equiv-x\]
түзуінен жоғары
орналасқан
\[I{\tilde{\sigma}}\delta\]
жазықтығының бөлігі.
4.
\[z=\sqrt{y-x^{2}}\,.\]
Жауабы:
\[\scriptstyle y=x^{2}\]
параболасынан жоғары
орналасқан
\[I{\tilde{\sigma}}\delta\]
жазықтығының бөлігі.
Берілген функциялардың дербес туындыларын табу керек.
5.
\[z=7x^{3}y-4x y^{5}.\]
Жауабы:
\[{\frac{\P[z}{\P[x}}=21x^{2}y-4y^{5};\,\,\,{\frac{\P[z}{\P y}}=7x^{3}-20x y^{4}.\]
6.
\[z=x^{4}+5x^{2}y+7y^{2}-\,6x-3y.\]
Жауабы:
\[{\frac{\P[z}{\P[x}}=4x^{3}+10x\,y-\,6;\ {\frac{\P[z}{\P y}}=5x^{2}+14y-3.\]
7.
\[z={\frac{y+3}{x+7}}.\]
Жауабы:
\[{\frac{\|{\boldsymbol{z}}}{\|{\boldsymbol{x}}}}=-\;{\frac{y+3}{\left(x+7\right)^{2}}}\cdot\quad{\frac{\|{\boldsymbol{z}}}{\|{\boldsymbol{y}}}}={\frac{1}{x+7}}.\]
8.
\[z={\frac{x}{y-5}}.\]
Жауабы:
\[{\frac{\|z}{\P(x}}={\frac{1}{y-5}};\quad{\frac{\P z}{\P|y}}=-\ {\frac{x}{(y-5)^{2}}}.\]
9.
\[z=a r c t g\frac{x}{y}.\]
Жауабы:
\[{\frac{\Psi[z}{][x}}={\frac{y}{x^{2}+y^{2}}};\quad{\frac{\Psi[z}{\P y}}=-\ {\frac{x}{x^{2}+y^{2}}}.\]
10.
\[z=\ln{\frac{y^{3}}{x}}.\]
Жауабы:
\[{\frac{\vert z}{\P x}}=-\ {\frac{1}{x}};\quad{\frac{\Vert z}{\Vert y}}={\frac{3}{y}}.\]
11.
\[z=\sin(x^{2}+y^{2}).\]
Жауабы:
\[{\frac{\|z}{\|x}}=2x\mathrm{cos}(x^{2}+y^{2});\;\;{\frac{\|z}{\|y}}=2y\mathrm{cos}(x^{2}+y^{2}).\]
12.
\[z=\cos_{\hat{Q}}{\frac{\mathbf{a}x}{\mathbf{\hat{Q}}}}\]
Жауабы:
13.
\[z=e^{x y}.\]
Жауабы:
\[{\frac{\mathrm{d}[z}{\Vert x}}=\partial\widetilde{a}^{\widetilde{\theta}\delta};\quad{\frac{\P[z}{\P[y}}=\widetilde{\theta}\widetilde{a}^{\widetilde{\rho}\delta}.\]
14.
\[z={\frac{x^{2}}{y^{2}}}+{\frac{x}{y}}.\]
Жауабы:
\[{\frac{\P z}{\P[x}}={\frac{2x}{y^{2}}}+{\frac{1}{y}};\quad{\frac{\P z}{\P y}}=-\ {\frac{2x^{2}}{y^{3}}}-{\frac{x}{y^{2}}}.\]
15.
\[u={\frac{x}{y}}+{\frac{y}{z}}+{\frac{z}{x}}.\]
Жауабы:
\[{\frac{\P u}{\P x}}={\frac{1}{y}}-\,{\frac{z}{x^{2}}};\,{\frac{\P[u}{\ P]}}=-\,{\frac{x}{y^{2}}}+{\frac{1}{z}};\,{\frac{\P[u}{\P z}}=-\,{\frac{y}{z^{2}}}+{\frac{1}{x}}.\]
16.
\[{\cal W}=\sqrt{{\cal X}^{2}+{\cal y}^{2}+{\cal z}^{2}}.\]
Жауабы:
\[\frac{\P(u}{\P x}=\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}};\;\;\frac{\P(u}{\P y}=\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}};\;\;\frac{\P[u}{\P z}=\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}.\]
Берілген функциялардың толық дифференциалдарын табу керек.
17.
\[z=x^{2}+5x y+6y^{2}.\]
Жауабы:
\[d z=(2x+5y)d x+(5x+12y)d y.\]
18.
\[z={\frac{y-4}{x+5}}.\]
Жауабы:
\[d z=\frac{y-4}{\left(x+5\right)^{2}}\,d x+\frac{1}{x+5}\,d y.\]
19.
\[z=7x^{3}y-4x y^{5}.\]
Жауабы:
\[d z=(21x^{2}y-4y^{5})d x+(7x^{3}-20x y^{4})d y.\]
20.
\[z={\frac{x-1}{y+2}}.\]
Жауабы:
\[d z=\frac{d x}{y+2}-\,\frac{x-1}{(y+2)^{2}}d y.\]
Бақылау сұрақтары
Екі айнымалының функциясы қалай анықталады?
Екі айнымалының функциясының қандай геометриялық мағынасы бар?
Екі және одан да көп айнымалының функциясының анықталу облысы деген не?
Дербес туындылар қандай ережелермен табылады?
Функцияның толық дифференциалын жуықтап есептеулерде қалай қолданылады?
2-дәріс. Көп айнымалылы функциялардың жоғары ретті дербес туындылары мен дифференциалдары
\[z\longrightarrow\bar{f}(x,y)\]
функциясының
екінші ретті дербес туындысы
деп осы функцияның бірінші ретті дербес туындысының дербес туындысын айтады және оны былай белгілейді:
\[z\longrightarrow\beta(x,y)\]
функциясының
екінші ретті дифференциалы
деп осы функцияның дифференциалының дифференциалын айтады және ол
\[d^{2}z={\frac{\P^{2}z}{d x^{2}}}\,d x^{2}+2{\frac{\P^{2}z}{\P x\Vert y}}\,d x d y+{\frac{\P^{2}z}{\partial y^{2}}}\,d y^{2}\]
формулаларымен анықталады.
1-мысал.
\[z=x^{3}+5x^{2}y\,-\,4y^{3}\,-\,x^{2}\,-\,6x y+3y^{2}\]
функциясының екінші ретті дербес туындыларын және екінші ретті дифференциалын табу керек.
Шешуі. Алдымен дербес туындыларын табайық:
\[{\frac{\P[z}{\P[x}}=3x^{2}+10x y-\,2x-\,6y,\ \ \ \ {\frac{\P[z}{\P[y}}=5x^{2}-12y^{2}-6x+6y.\]
\[{\frac{\mathbb{R}^{2}z}{\|x^{2}}}={\frac{\Phi[\mathbf{\Lambda}_{\Lambda}^{2}{\bar{\mathbf{c}}}_{\bar{\Lambda}}}{\|x_{\tilde{\alpha}}^{2}{\bar{\phi}}}}=6x+10y-2,\]
\[{\frac{\P^{2}z}{\P y^{2}}}={\frac{\Phi[}{\P y}}{\frac{\alpha^{\alpha}]z}{\P}}{\frac{\ddot{\Phi}}{\Phi}}=-\,24\,y+6,\qquad{\frac{\P[}{\Phi}}{\frac{\alpha^{\alpha}z}{\P}}={\frac{\Phi[}{\P y}}{\frac{\alpha^{\tilde{\alpha}}[z}{\P}}{\frac{\breve{\Phi}}{\Phi}}=10x-6,\]
\[\begin{array}{l}{{d^{2}z=\frac{\Phi[^{2}z}{\Phi[x^{2}}d x+2\frac{\P^{2}z}{\P[x]y}d x d y+\frac{\P^{2}z}{\P y^{2}}d y^{2}=}}\\ {{=(6x+10y-2)d x^{2}+2(10x-6)d x d y+(-24y+6)d y^{2}.}}\end{array}\]
Күрделі функцияны дифференциалдау
Дифференциалданатын
\[z\longrightarrow P(M,\nu)\]
функциясы берілсін, мұнда
\[u=u(x,y),\nu=\nu(x,y)\]
функциясының дербес туындылары
формулаларымен есептеледі.
2-мысал.
\[z=\cos(u^{2}+\sqrt{\nu})\]
функциясының, мұндағы
\[u=e^{x y},\nu=x^{2}+y^{2}\]
, дербес туындыларын табу керек.
Шешуі.
\[{\frac{\|z}{\|x}}={\frac{\Vert z}{\|_{t}u}}{\frac{\Vert u}{\Vert x}}+{\frac{\Vert z}{\Vert y}}{\frac{\Vert y}{\Vert x}}=-\ \mathrm{sin}(u^{2}+{\sqrt{\nu}})\times\!u\rtimes\!v_{x}^{'}\!-,\]
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Меншіксіз интегралдар: Лаплас түрлендіруі, көп еселі интегралдар, әдістері және теңдеулерге қолданылуы Көп айнымалы функциялардың интегралдық есептеулері: екі және үш еселі интегралдар мен қолданылуы Туынды және дифференциал: элементар функциялардың туындылары, геометриялық мағына және көп айнымалы функциялардағы толық дифференциал Анықталмаған және анықталған интегралдар мен интегралдау әдістері; көп айнымалы функциялар: дербес туындылар, градиент және Лагранж әдісі арқылы шартты экстремум Бір және көп негізді карбон қышқылдары: құрылымы, физика-химиялық қасиеттері, алыну әдістері және туындылары Көп айнымалы функциялар теориясы: Евклидтік кеңістік, үзіліссіздік, туындылар және айқындалмаған функциялар Екі және үш еселі интегралдар мен сандық қатарлардың жинақталу критерийлері Аралас туындылар туралы теорема, жоғарғы ретті толық дифференциалдар, екі айнымалылы функциялар үшін Тейлор формуласы және экстремумдар Координаталар әдісі: координаттық жүйелер, түрлендірулер және еселі интегралдар Екі еселі, үш еселі, беттік және қисық сызықты интегралдар: теориясы, есептеу әдістері және физикадағы қолданылуы


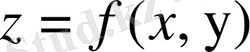 функциясы анықталатын
х
және
у
мәндерінің қос
(
функциясы анықталатын
х
және
у
мәндерінің қос
(
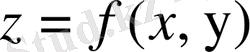 функциясының анықталу облысы
функциясының анықталу облысы
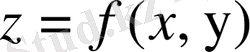 функциясының
функциясының
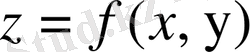 функциясы және
функциясы және
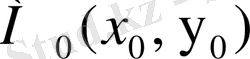 нүктесіне ұмтылғандағы
нүктесіне ұмтылғандағы
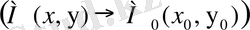 шегі деп айтады және оны былай белгілейді
шегі деп айтады және оны былай белгілейді
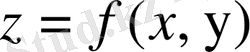 функциясы
функциясы
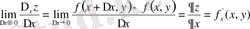
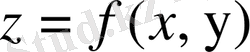 функциясының
у айнымалысы бойынша дербес туындысы
деп
функциясының
у айнымалысы бойынша дербес туындысы
деп
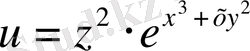 функциясының дербес туындыларын табу керек.
функциясының дербес туындыларын табу керек.