Көп компонентті қоспалардағы дәрілік заттарды өлшеу әдістемелері мен анықтау алгоритмдерін әзірлеу


Қазақстан Республикасы Білім және Ғылым министрлігі
Академик Е. А. Бөкетов атындағы
Қарағанды университеті
Еркінбек Гүлназ
Жасан Айдана
Жүніс Назерке
Ауез Назира
Асанқызы Майгүл
ДИПЛОМДЫҚ ЖОБА
5В074800-«Фармацевтикалық өндіріс технологиясы» мамандығы
Қарағанды 2022
Қазақстан Республикасы Білім және Ғылым министрлігі
Академик Е. А. Бөкетов атындағы
Қарағанды университеті
«Қорғауға жіберілді»
Органикалық химия және полимерлер
кафедрасының меңгерушісі
х. ғ. к., доцент Т. С. Жұмағалиева
ДИПЛОМДЫҚ ЖОБА
Тақырыбы: «Көп компонентті қоспалардағы дәрілік заттарды өлшеу әдістемесі және анықтау алгоритімдерін әзірлеу»
5В074800-«Фармацевтикалық өндіріс технологиясы» мамандығы
Орындағандар: Еркінбек Гүлназ
Жасан Айдана
Жүніс Назерке
Ауез Назира
Асанқызы Майгүл
Ғылыми жетекші, Сәрсенбекова А. Ж.
PhD доктор, доцент:
Қарағанды-2022
Академик Е. А. Бөкетов атындағы Қарағанды унивеситеті
Факультет:Химия
Мамандық:5В074800-«Фармацевтикалық өндіріс технологиясы»
Кафедра:Физикалық және аналитикалық химия
«Бекітемін»
Кафедра меңгерушісі
х. ғ. к., доцентЖумагалиева Т. С
«__»__2022ж
Дипломдық жобаны орындауға
ТАПСЫРМА
Студенттер Жасан А. Ж., Еркінбек Г. Қ., Жүніс Н. А., Ауез Н. М., Асанқызы М.
аты-жөндері
4 курс, ТФП-414, күндізгі
курсы, тобы, мамандығы, оқу түрі
- Дипломдық жобаның тақырыбы:«Көп компонентті қоспалардағы дәрілік заттарды өлшеу әдістемесі және анықтау алгоритімдерін әзірлеу» 2022ж. №.
- Студенттің аяқталған жұмысты тапсыру мерзімі «» 2022 ж.
- Жұмысқа бастапқы мәлеметтер (заңдар, әдеби көздер, зертханалық
өндірістік мәлеметтер) Пайдаланылған дереккөздерді талдау жұмыстары келесі журналдардың негізінде жасалған:
1. Петров Б. И., Афендикова Г. Ю. Об устранении основного недостатка процессов жидкостной экстракции неорганических соединений // Журн. прикл. химии. 1985. Т. 85, № 10. С. 2194-2199.
2. Петров В. И., Яковлева Т. П., Чукин В. М., Егорова Л. С. Образование новых экстракционных систем при протолитическом взаимодействии и высаливании органических соединений // Журн. прикл. химии. 1993. Т. 66, № 8. С. 1751-1756.
3. Черкасов Д. Г., Смотров М. П., Ильин К. К. Равновесие жидкость-жидкость и критические явления в тройной системе вода-пиридин-масляная кислота в интервале 5-55°С // Журн. прикл. химии. 2008. T. 81, № 2. С. 229-233.
4. Петров Б. И., Пригожин С. И. Аналитическое использование экстракции элементов в расслаивающейся системе вода-антипирин-монохлоруксусная кислота // Журн. аналит. химии. 1985. Т. 40, № 2. С. 247-251.
5. Чепурина З. В. Влияние солей на фазовое поведение тройных жидкостных систем с замкнутой областью расслоения : автореф. дис. … канд. хим. наук. Саратов, 2015. 23 с.
6. Химическая энциклопедия : в 5 т. / гл. ред. И. Л. Кнунянц. М. : Сов. энциклопедия, 1988-1998.
7. Черкасов Д. Г., Курский В. Ф., Ильин К. К. Топологическая трансформация фазовой диаграммы тройной системы нитрат цезия-вода-ацетонитрил // Журн. неорган. химии. 2008. Т. 53, № 1. С. 146-152.
8. Аносов В. Л., Озерова М. Н., Фиалков Ю. Я. Основы физико-химического анализа М. : Наука, 1976. 504 с.
9. Ильин К. К., Никурашина Н. И. Изучение фазовых равновесий тройной системы вода-пиридин-хлорид калия в интервале температур 0-160°C // Журн. прикл. химии. 1980. Т. 53, № 10. С. 2211-2215.
10. Черкасов Д. Г., Чепурина З. В., Ильин К. К. Фазовые равновесия и критические явления в тройной системе нитрат цезия-вода-масляная кислота в интервале температур 5-100°C // Журн. физ. химии. 2015. Т. 89, № 8. С. 1258-1263.
11. Смотров М. П., Черкасов Д. Г., Ильин К. К. Фазовые равновесия и критические явления в тройной системе нитрат цезия-вода-пиридин // Журн. неорган. химии. 2017. Т. 62, № 3. С. 375-380.
4. Дипломдық жобада өңдеуге жататын мәселелер тізімі:
1) Су-изо-май қышқылының екілік жүйесіндегі фазалық диаграммасы
2) Су-қ-бутил спиртінің қос жүйесіндегі фазалық тепе-теңдік және сыни құбылыстар
3) Үштік жүйенің фазалық диаграммасының топологиялық өзгеруі 40-140°C температура аралығында калий перхлораты−су−твин-80
4) Фазалық тепе-теңдік және сыни құбылыстар үштік жүйеде цезий нитраты−су−твин-805-100ºС температура аралығында
5) Практикалық түрде жүзеге асыру
5. Графикалық материалдар тізімі (сызбалар, кестелер, диаграммалар және
т. б. ) Кестелер, реакция сызбалары, ИК, ЯМРспекторларының нәтижелері
6. Негізгі ұсынылатын дереккөздер тізімі
1. Химическая энциклопедия / Ред. И. Л. Кнунянц. М. : Сов. энциклопедия, 1988-1998. Т. 1-5.
2. Dan Wu, Hao Chen, Ling Jiang, Jin Cai, Zhinan Xu, Pei- lin Cen // Chin. J. Chem. Eng. 2010. V. 18. № 4. P. 533.
3. Крупаткин И. Л., Роженцова Е. П. // Изв. вузов. Хи- мия и хим. технология. 1971. Т. 14. № 8. С. 1196.
4. Черкасов Д. Г., Ильин К. К. // Журн. прикл. химии. 2009. Т. 82. № 5. С. 864.
5. Черкасов Д. Г., Смотров М. П., Ильин К. К. //Там же. 2008. Т. 81. № 2. С. 229.
6. Cherkasov D. G., Kurskii V. F., Il’in K. K. // Russ. J. In- org. Chem. 2008. V. 53. №. 1. P. 139. DOI: 10. 1134/S0036023608010208
7. Кузнецова И. К., Бергман А. Г. // Журн. общ. химии. 1956. Т. 26. № 5. С. 1335.
8. Крупаткин И. Л., Роженцова Е. П. // Журн. физ. хи- мии. 1970. Т. 44. № 4. С. 1036.
9. Киргинцев А. Н., Трушникова Л. Н., Лаврентьева В. Г. Растворимость неорганических веществ в воде: Справочник. Л. : Химия, 1972. 248 с.
10. Справочник по растворимости: Бинарные систе- мы / Под ред. В. В. Кафарова. Т. 1. Кн. 1. М. ; Л. : Изд-во АН СССР, 1961. 960 с.
11. Черкасов Д. Г., Ильин К. К. X Междунар. Курнаков- ское совещ. по физико-химическому анализу: Сб. тр. в 2 томах. Т. 1. Самара: Самар. гос. техн. ун-т, 2013. С. 57.
12. Пиркес С. Б., Лапицкая А. В., Макушова Г. Н. Исследо- вание термического разложения о-метоксибензоатов цериевой подгруппы // Журн. неорг. химии. 1976. Т. 21, No 6. С. 1494-1497
13. Макушова Г. Н., Лапицкая А. В., Гоппе С. О., Пир- кес С. Б. Термографическое и термогравиметрическое исследование соединений РЗЭ иттриевой подгруп- пы // Журн. неорг. химии. 1979. Т. 24, No 10. С. 2828-2830.
14. Maia J. D. C., Carvalho G. A. U., Mangueira C. P. Jr., Santana S. R., Cabral L. A. F., Rocha G. B. GPU Linear Algebra Libraries and GPGPU Programming for Ac- celerating MOPAC Semiempirical Quantum Chemistry Calculations // J. of Chem. Theory and Computation. 2012. Vol. 8. P. 3072-3081.
15. Dutra J. D. L., Filho M. A. M., Rocha G. B., Freire R. O., Simas A. M., Stewart J. J. P. Sparkle PM7 Lanthanide Parameters for the Modeling of Complexes and Mate- rials // J. Chem. Theory Comput. 2013. Vol. 13, iss. 9 (8) . P. -3341.
Тапсыра
алу мерзімі
Тапсырманы
берді
(қолы)
Тапсырманы
қабылдады
(қолы)
8. Дипломдық жобаны орындау кестесі
Жұмыс кезеңдерін
орындау
мерзімдері
Қыркүйек
2021ж
Дипломдық жоба дайындау үшін
материалдар жинау
Желтоқсан
2021ж
Дипломдық жобаның
теориялық бөлімін дайындау (1 тарау)
Қаңтар-наурыз
2022ж
Дипломдық жобаның
сараптамалық бөлімін дайындау (2-3 тарау)
Дипломдық жобаның толық
мәтінінің жобалық нұсқасын аяқтау
Сәуір
2022ж
Сәуір
2022ж
Сәуір
2022ж
Дипломдық жобаның ғылыми
жетекшінің пікірімен және сын-пікірмен ұсыну
Сәуір
2022ж
Мамыр
2022ж
Тапсырманың берілген күні « » қараша 2022 ж.
Ғылыми жетекшісі Сарсенбекова А. Ж.
қолы аты-жөні, ғылыми атағы, қызметі
Тапсырманы қабылдады: студенттер Жасан А. Ж.,
Еркінбек Г. Қ.,
Жүніс Н. А.,
АуезН. М.,
Асанқызы М.
қолы аты-жөні
МАЗМҰНЫ
НОРМАТИВТІК СІЛТЕМЕЛЕР
Осы дипломда мынадай стандарттарға сілтемелер пайдаланылады:
МС 6. 38-90. Құжаттардың жүйелерін сәйкестендіру. Ұйымдастыру-өкімдік құжаттаманың үлгісі. Құжаттарды ресімдеуге қойылатын талаптар.
МС 7. 1-84. Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Құжаттың библиографиялық сипаттамасы. Жалпы талаптар және құрастыру ережелері.
МС 7. 9-95 (ИСО 214-76) . Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Реферат және аннотация. Жалпы талаптар.
МС 7. 12-93. Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Библиографиялық жазба. Орыс тіліндегі сөздерді қысқарту. Жалпы талаптар және ережелер.
МС 7. 54-88. Ақпарат, кітапхана және баспа ісі бойынша стандарттар жүйесі. Ғылыми-техникалық құжаттарда заттар мен материалдардың қасиеттері туралы сандық деректерді ұсыну. Жалпы талаптар.
МС 8. 417-81. Өлшем бірлікті қамтамасыз етудің мемлекеттік жүйесі. Физикалық шамалар бірліктері.
МС 1770-74. Зертханалық шыны өлшеуіш ыдыс. Мензуркалар, колбалар, пробиркалар. Жалпы техникалық шарттар.
МС 3885-73. Реактивтер және аса таза заттар. Сынамаларды іріктеу орау, қаптау және таңбалау.
МС 23932-90 Е. Зертханалық шыны ыдыстар мен жабдықтар.
МС 25336-82. Зертханалық шыны ыдыстар мен жабдықтар. Түрлері, негізгі параметрлері және өлшемдері.
ҚОЛДАНЫЛҒАН БЕЛГІЛЕР МЕН ҚЫСҚАРТУЛАР
ТСЖ-Тізбекті симплексті жоспарлау.
ЖКЕТ-жоғарғы кризимтік еріту температурасы.
КС-критикалық сұйық.
ТФЭ -толық факторлы эксперимент.
КІРІСПЕ
Қазіргі заманғы медицина мен фармацияда қолданылатын материалдар өте сирек Д. И. Менделеев. Әдетте, олар бірнеше элементтерден тұрады - компоненттер. Өнеркәсіптік препараттардағы компоненттердің саны кейде айтарлықтай көп. Бірақ қазірдің өзінде жүйені құрайтын екі компонент бар, араластыру нәтижесі өте күрделі, әртүрлі және жаһандық қабылдау үшін қиын болуы мүмкін.
Пайда болған қиындықты айналып өту үшін олар кейінгі тәжірибе көрсеткендей, жалғыз әдіске жүгінді. Екілік және көп компонентті жүйелердің қасиеттері күй диаграммалары (фазалық диаграммалар) түрінде көрсетіле бастады, олар фазалық тепе-теңдік термодинамикасында өзіндік иероглифтер рөлін атқара бастады.
Екілік жүйелер үшін T-x және p-x диаграммалары сияқты «иероглифтер» кеңінен қолданылады. Біріншісі тұрақты қысымдағы көлемдік күй диаграммасының бөлімі, ал екіншісі тұрақты температурада. Диаграммалар инициаторға фазалардың санын, химиялық табиғаты мен құрамын, фазалардың болу шекарасын, компоненттердің өзара әрекеттесу сипатын және жаңадан түзілген қосылыстардың болуын анықтауға мүмкіндік береді. Олар әртүрлі әдістермен алынған сәйкес эксперименттік мәліметтер негізінде құрастырылған.
Фармацияда «үйлесімсіздік» термині белгілі және кеңінен қолданылады. Үйлесімсіздік - дәрілік заттардың бастапқы химиялық, физикалық және фармакодинамикалық қасиеттерін өзгертетін және олардың сапасының нашарлауына әкелетін процесс. Күй диаграммаларын пайдалана отырып, «физикалық сәйкессіздікті» (ұнтақтарды ылғалдандыру, эмульсияларды бөлу) және «химиялық үйлесімсіздікті» (жаңа қосылыстардың түзілуімен құрамдастардың өзара әрекеттесуін) болжауға және жоюға болады.
Негізді таңдау жүзеге асырылатын жетекші көрсеткіштердің бірі балқу (кристалдану) температурасы болып табылады. Суппозиторийлерді жасау үшін дәрілік формалардың балқу температурасын қамтамасыз ететін негіз қажет. Негізге қосымша енгізілген заттар оның механикалық қасиеттерін және балқу температурасын өзгертеді. Осыған байланысты әртүрлі көмекші және дәрілік заттар мен олардың комбинациясы үшін компоненттердің әртүрлі қатынасы бар негіздер қажет. Оңтайлы балқу температурасына қол жеткізу үшін LF және қосалқы заттардың негізін таңдау мәселесі күйдің фазалық диаграммаларын қолдану арқылы сәтті шешілуі мүмкін.
Бұл зерттеудің мақсаты сәйкес жүйелер үшін балқу диаграммаларын құру арқылы LF өндірісінде негіз ретінде қолданылатын қоспалардың балқу (қатығу) температуралық диапазондарына қосымша заттар ретіндегі қоспалардың әсерін зерттеу болды.
Осы мақсатқа жету үшін келесі міндеттер қойылды:
- су- і -май қышқылының екілік жүйесіндегі фазалық диаграммасын зерттеу;
- су- қ- бутил спирті екілік жүйесіндегі фазалық диаграммасын зерттеу;
- калий перхлораты-су-твин-80 жүйесіндегі фазалық өзгерістерді зерттеу;
- цезий нитраты-су-твин-80 жүйесіндегі фазалық өзгерістерді зерттеу.
Ғылыми жаңалық. Жұмыста бірінші рет:
- су -і- май қышқылының екілік жүйесіндегі фазалық тепе-теңдік пен критикалық құбылыстар визуалды-политермиялық әдіспен 10-30°С диапазонында зерттелді;
- су- қ -бутил спиртінің қос жүйесіндегі фазалық тепе-теңдік және сыни құбылыстары 10-125°С аралығында визуалды-политермиялық әдіспен зерттелді;
- калий перхлораты-су-твин-80 жүйесінің температуралық концентрациялық призмасының салынған изотермиялық бөлімдерін талдау үш еселік жүйелердің фазалық диаграммаларының топологиялық трансформациясының заңдылықтарын анықталды;
- калий перхлораты-су-твин-80 жүйесінің температуралық концентрациялық призмасының салынған изотермиялық бөлімдерін талдау үш еселік жүйелердің фазалық диаграммаларының топологиялық трансформациясының заңдылықтарын анықталды;
- цезий нитраты−су−твин-80 жүйесінің температуралық концентрациялық призмасының салынған изотермиялық бөлімдерін талдау үш еселік жүйелердің фазалық диаграммаларының топологиялық трансформациясының заңдылықтарын анықталды.
Зерттеу объектісі: жұмыста еріткіштер ретінде су және i -майқышқылы, қ -бутил спирті, твин-80 қолданылды. Еріткіштер қайнау температурасы, сыну көрсеткіші және тығыздығы бойынша анықталды, олардың физикалық тұрақтылары анықтамалық деректермен өлшеу қателігі шегіне сәйкес келді.
Зерттеу әдістері: Жүйе компоненттерінің қоспаларындағы фазалық тепе-теңдік визуалды-политермиялық әдіспен шыны ампулаларда (10-30°Сжәне 0-100°С) температура диапазонында бу қысымында зерттелді. Ерітіндінің критикалық нүктесіне сәйкес келетін ерітіндінің құрамы сұйық фазалардың көлемдерінің қатынасы әдісімен эксперименталды түрде анықталды және фазалық жүйелік диаграмманың деламинация өрісіне Алексеев диаметрін салу арқылы графикалық түрде расталды.
Қажетті температура Lauda A-100 термостатының және 0. 1°C қателігі бар Krio-vist-T-05 төмен температуралы термостаттың көмегімен сақталды және сол қателікпен калибрленген ондық сынапты термометрлермен өлшенді. Компоненттер қоспаларындағы сұйық-сұйық тепе-теңдік 1 сағат ішінде орнатылды, сұйық және қатты фазалардың тепе-теңдігіне қоспаны үздіксіз араластыру арқылы 3 сағаттан кейін жетті. Тепе-теңдікті орнатудың белгісі фазалық ауысулардың температураларын өлшеу нәтижелерінің оларға төменгі және жоғары температуралар жағынан жақындаған кезде қайталануы болды.
Жұмыстың ғылыми және тәжірибелік маңыздылығы:Жұмыста ұсынылған тәсілді жақсартылған дәрілік заттардың дисперсті түрлерін алу үшін қолдануға болады.
1. 1 Есепті шешу реттілігі
Оптимизация есептерін шешу үшін 1 кесте көрсетілген сызбаны пайдаланады.
1 кесте .
Бокс-Уилсон әдісімен есепті шешудің жалпы схемасы
Есептің қойылуы
↓
Тәжірибе жоспарын құру
↓
Тәжірибе жоспарын іске асыру
↓
Математикалық модель құру
↓
Модельді статистикалық талдау
↓
Нәтижелерді түсіндіру
↓
Тапсырманы шешудің жеке кезеңдеріне тоқталамыз. Зерттеу мақсатын сандық тұжырымдаудан бастайды. Мақсатты тұжырымдау ең алдымен оңтайландыру параметрін таңдауды қамтиды. Егер бір уақытта бірнеше сипаттаманы оңтайландыру қажет болса, онда не бірнеше оптимизациялау параметрлері біреуге дейін азаяды, немесе тапсырманы ортақ шешу керек.
Содан кейін факторларды таңлайды. Көбіне бұл күрделірек мәселе. Егер факторлар көп болса, онда бір бөлігі экспериментальды немесе априорлы түрде жойылады. Әрі қарай негізгі деңгей және фактордың өзгеру аралықтары таңдалады. Ұсыныстардың бірі - факторды анықтауда вариация интервалы орташа квадраттық қатеден 2 есе көп болуы керек.
Факторлар келесідей кодталады:
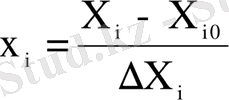 (1)
(1)
Мұндағы: xi-кодталған, ал Xi i-ші фактордың табиғи мәні. Xi0 - негізгі деңгейдегі i-ші фактордың табиғи мәні.
Кодтау фактордың жоғарғы деңгейін +1, төменгі деңгейін -1, ал негізгі деңгейін нөл түрінде көрсетеді. Немесе одан дәлірек +, -0. Кодтау әртүрлі факторлардың оңтайландыру параметріне әсер ету күшін салыстыруға мүмкіндік береді. Факторларды кодтау 2 кесте көрсетілген.
2 кесте.
Факторларды кодтау схемасы
Мысал: Бөлшектердің қаттылығын кемінде 350 HB қамтамасыз ету үщін ескірген мыс негізіндегі қорытпаны термиялық өңдеу режимін таңдау керек.
Оңтайландыру параметрлері (Y) -қорытпаның қаттылығы.
3 кестеде
Зерттелетін факторлар және олардың өзгеру сипаты көрсетілген
Қыздыру уақыты
0C
Төзу уақыты
0C
Бұзылу уақыты
мин
Бұзылу температурасы
0C
1. 2 Эксперимент жоспарын құру
ТФЭ (толық факторлы эксперимент) жоспарын жасау кезінде эксперименттердің қайталанбауын қадағалау керек. Тәжірибелер аз болса қиын болмайды, олардың санының өсуімен қиын болады. Қайталануды болдырмау үшін, 1 кестеде көрсетілген принципті қолдануға болады.
Тәжірибе жүргізу шарттары мынадай түрде кодталған:
- факторлар латын әліпбиінің a, b, c, d, e және т. б. әріптерімен белгіленеді;
- егер тәжірибеде осы факторды кодтайтын әріп болса, ол жоғарғы деңгейде, егер жоқ болса төменгі деңгейде қабылданады.
- егер тәжірибеде барлық факторлар төменгі деңгейде болса, онда тәжірибе түсіндіреді (1) .
Матрицаларды дәл осылай кодтау, жүйелі түрде көрсетуге мүмкіндік береді.
4 кесте.
Толық тәжірибенің матрицасы 22 ден 25 ке дейін
ЖОСПАР Тәжірибе номері, №
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz