Жел электр станциясы үшін тороидальды желкеннің геометриясын есептеу және аэродинамикалық бағалау


Желкенді жел электр станциясы үшін тороидальды желкенді таңдау
Жел электр станциясын қолданудың негізгі міндеттерінің бірі жел энергиясын пайдалану тиімділігін арттыру болып табылады. Көлденең және тік роторлары бар жел электр станцияларының пайдалы әрекет күшінің коэффициенті Бенц коэффициентінен аспайтыны белгілі [1, 2] . Бірқатар ғалымдар, мысалы, Абдолрахим Резаейха, Берт Блоккен[ 3], Росарио Ланцафаме [4] өз еңбектерінде ЖЭС тиімділігін арттыру мақсатында жаңа және жетілдірілген ЖЭС жұмыс органдарын сынау үшін виртуалды аэродинамикалық құбырлар түрінде компьютерлік бағдарламаны қолданды. Дегенмен, жел екпінінің болжанбауы жағдайында ЖЭС-тің ПӘК-ін ұлғайту және ЖЭС жұмысына байланысты проблемаларды жою жөніндегі міндет бүгінгі күнге дейін өзекті болып отыр.
Мақалада тербелмелі жұмыс органы бар желкенді ЖЭС ұсынылады [5] .
1-суретте екі бөліктен тұратын желкенді жел электр станциясының демонстрациялық моделі көрсетілген: 10 мачтадан және 11 тороидальды желкеннен тұратын жұмыс органы, сондай-ақ SHOLKOR платформалық манипуляторынан манипулятор түрлендіргіші [6] .
Тороидальды парустың көлденең қимасы үшін ұшақтың Р-II-14% (ЦАГИ-718) қанатының профилі қабылданады, өйткені ол қажетті көтеру күшін қамтамасыз етеді және желдің кинетикалық энергиясын тиімді пайдалануға мүмкіндік береді. Тороидальды желкеннің диаметрлі жазықтығы белгілі бір бұрышқа ауытқыған кезде жел ағыны үзілетін етіп таңдалады. Осылайша, тороидальды желкеннің көтеру күші мен қарсылық күші азаяды. Тороидалды желкен мен желкенді жел электр станциясының тағы бір ерекшелігі - жел электр станциясының жұмысы желдің қай бағыттан соғатындығынан тәуелді емес, желкенді жел электр станциясы қосымша реттеуді және желкеннің жел соғатын жағына қарай жағдайының өзгеруін қажет етпейді. Бұл желкенді ЖЭС жұмыс органының салмағын азайтады және қосымша құрылғылар үшін шығындарды қажет етпейді.

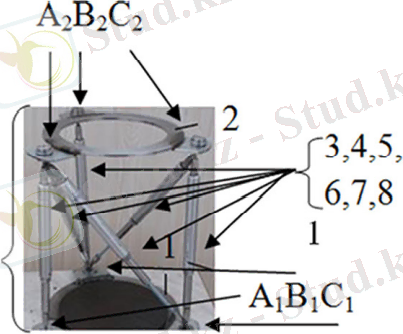
1 Сурет - Желкенді жел электр станциясының демонстрациялық моделі
Желкенді ЖЭС 10 діңгегі (мачта) берік және жеңіл материалдан жасалған. Мачтаның функциясы тороидальды парустың тербелісінің механикалық энергиясын платформалық манипуляторға жоғалтпай беру болып табылады.
SHOLKOR 9 платформалық манипуляторы 1 платформасының жоғарғы жағынан және 2 платформасының төменгі жағынан тұрады [7] . 10 Мачта платформалық манипулятордың 1-нің жоғарғы жылжымалы бөлігіне қатаң бекітілген. Плавтформалық манипулятордың төменгі бөлігі негізге (діңгегіне) қатаң бекітіледі. Жоғарғы платформа 1 және төменгі платформа 2 өзара алты қозғалмалы актуаторлармен 3-8 А 1 , В 1 , С 1 , А 2 , В 2 , С 2 байланыс нүктелері арқылы байлнысады. Актуаторлар бір-бірімен сфералық байланыс немесе жаңа патенттелген кабельдік байланыс арқылы қосылған. Бұндай байланыс тәсілдері платформалық манипулятордың жоғарғы бөлігіне кеңістікте еркін орын алмастыруға мүмкіндік береді. Белгілі сызықтық генераторларды актуаторлармен параллель қосып, жұмыс органынан электр энергиясын өндіруге болады.
Желкенді жел электр станциясының тороидалды желкенін ары қарай жобалау үшін тороидалды желкеннің геометриялық өлшемдерінің есептеу алгоритмін құру қажет.
Желкен ұшақ қанатының аэродинамикалық профилі түрінде көлденең қимасы бар тороидальды пішінге ие. Аэродинамикалық профильдің қимасының периметрін есептеу үшін аналитикалық тәуелділіктер болмағандықтан, аэродинамикалық профильдің периметрін анықтау үшін эллипс формасы қабылданды.
Тороидальды желкеннің беткі ауданын есептеу кезінде бірнеше ерекшеліктерді ескеру қажет, атап айтқанда айналу денесінің беті айналу осіне қатысты R эксцентриктілігіне ауысатын эллипс түрінде пайда болады.
Эллипс теңдеуі шеңберді бойымен анықталады:
Мұндағы a, b - эллипстің жартыосьтері.
Алынған теңдеудің П бұрышына айналу үшін сол жақтағы айналу матрицасын көбейтеміз:
және векторын қосу арқылы графикті х осімен 0арай жылжытамыз :
Алынған фигураны осіне қатысты айналдыру барысында үшөлшемді фигураны аламыз, оның бетінің ауданы келесі теңдікке тең:
мұнда
.
интегралында келесі алмастырулар: , , , жасай отырып, келесі теңдікті аламыз .
интегралымен ұқсас әрекеттер жасаймыз: алмастыру жолымен , , , , I 2 =0 екендігін аламыз.
Ендеше:
.
Туындылады алып және тригонометриялық түрлендірулер жасай отырып, келесі теңдікті табамыз:
Мына теңдікті аламыз:
,
Мұндағы - эллипс периметрі. интегралы қарапайым функцияларда шешімі болмайды. Оны жағдайындағы ɛ-ден тәуелді екінші типтегі эллиптикалық интеграл арқылы көрсетуге болады: . Алмастырулар жасау арқылы келесі теңдікті аламыз , мұндағы - эллипстің эксцентриситеті.
Соңында келесі теңдікті аламыз:
Бұл теңдік негізінен эллипс периметрі және у осіне қатысты айналу уақытында эллипстің центрі арқылы сипатталатын шеңбердің периметрінің туындысы болып табылады.
Сонымен тороидалды желкен бетінің ауданын есептеу үшін пен табу керек. табу үшін келесі формуламен эксцентриситетті және екінші ретті толық эллиптикалық интегралды Е(ɛ) табу қажет. Е(ɛ) -ны дайын кестелерден немесе 2-суретте көрсетілген диаграммадан алуға болады. Ол диаграммада шартында екінші ретті толық интегралдар берілген .
Тәжірибелік қолданыс үшін формулалармен есептеуге арналған жеңілдетілген алгоритмдер ұсынылады:
ɛ=𝜅, (1)
(2)
(2) формуладан - тің эллипстің параметрлеріне және тороидальды желкеннің шеңберіне тәуелділігі шығады:
(3)
3-суретте көрсетілгендей, - шеңбердің радиусы, - эллипстің хордасының ұзындығының жартысы, - эллипстің биіктігінің жартысы.
Ұшақтың қанатының аэродинамикалық профилінің формасы бекітілген өлшемдерге ие. Алайда ұшақтың қанатының әр профиліне аэродинамикалық профильдің биіктігі мен ұзындығының тәуелділігі әртүрлі. Таңдалған профиль Р-ІІ-14% (ЦАГИ-718) . Атауынан таңдалған профильдің биіктігі профильдің ұзындығының b=a ∙ 0. 14 14% тең екендігін білуге болады.
(3) формула негізінде тороидалды желкеннің геометриялық өлшемдерін есептеуге арналған бағдарлама құрастырылды. Тороидальды желкеннің геометриялық өлшемдерін есептеуге арналған бағдарламаның жұмыс принципі - тороидальды желкеннің беткі ауданы (S) және эллипстің ұзындығы (a) берілгендігімен түсіндіріледі. Бағдарлама тороидальдық желкен радиусының (r) мәнін және тороидальдық желкен профилінің аэродинамикалық қимасының биіктігін (b) бағдарлама экранына автоматты түрде шегереді және береді.
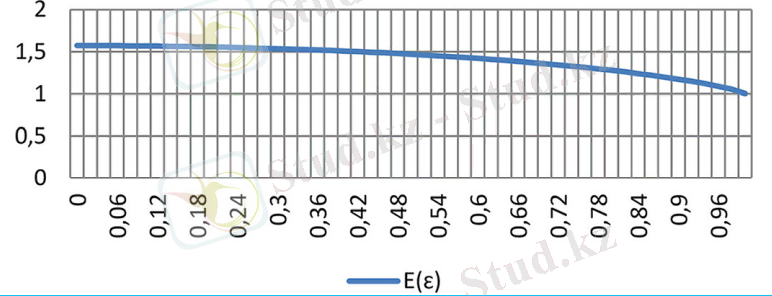
2 сурет - Эллиптикалық интеграл модулі мен екінші типтегі толық эллиптикалық интеграл арасындағы байланыс

3 сурет - Тороидалды желкен
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz