Әртүрлі типтегі және шешу әдістері мен тәсілдерінің алуан түрлілігі кезінде комбинаторлық есептерді шешудің жалпы тәсілдерін анықтау

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

І Кіріспе

Математиканың маңызды және елеулі бөлімдерінің бірі комбинаторика болып табылады. Комбинаторлық өнермен" әр адам таныс болу керек. Комбинаторлық есептердің шешу техникасын меңгерген, демек, ойлай білетін, шешімнің әр түрлі нұсқаларын таңдай білетін адамдар жиі қиын жағдайлардан шығу жолын тауып кетеді. Мұны үйрену үшін зерттеу қызметімен айналысу керек, яғни зерттеу, шешу, тану керек.
Біздің өмірімізге сайлау мен референдумдар, банк несиелері мен сақтандыру полистері, жұмыспен қамту кестелері мен әлеуметтік сауалнамалар диаграммалары кірді. Қоғам өзін тереңірек зерттеп, өзі туралы және ықтималдық туралы түсініктерді талап ететін табиғат құбылыстары туралы болжам жасауға ұмтыла бастады. Тіпті теледидар мен газеттер бойынша әлемдік нарықтардағы валюта болжамының мәліметтері ертең 5% баға белгіленімдерінің төмендеуі күтілуде деп хабарлайды. Әрине, бұл теорияның пайда болуы ғылымда кездейсоқ құбылыс болды ма?
Зерттеудің өзектілігі: Біз математика сабағында бірінші рет математиканың бір бөліміне жататын қызықты есептермен - коммбинаторикамен кездестік. Комбинаторлық есептер адамдардың практикалық қызметімен байланысты көптеген сұрақтарға жауап бере алады, есептерді шешу ақыл-ой қабілеттерін, логикалық ойлауды, есептеу дағдыларын дамытуға көмектеседі. Комбинаториканы білу әр түрлі мамандық өкілдеріне қажет. Комбинаторлық міндеттермен физиологтарға, лингвистерге, кодтар теориясы бойынша мамандарға іс жүргізуге тура келеді.
Комбинаториканың даму тарихын зерделей отырып, біз ғалымдардың осы саланы қалай дамытқанын және осы атауды бергенін ұғынамыз. Осының бәрі тұлғаның жан-жақты дамуы үшін қажет. Қазіргі заманның иесі жақсы математикалық дайындыққа ие болуы және өз білімі мен дағдыларын тәжірибеде қолдана білуі тиіс. Осы мақсатта біз комбинаторика мен оның дамуы туралы көбірек білуді , зерттеу жүргізуді қолға алдық.
Мен үшін ықтимал жағдайда өмір сүруді үйрену керек. Бұл дегеніміз ақпаратты алу, талдау және өңдеу, кездейсоқ нәтижелермен әр түрлі жағдайларда негізделген шешімдер қабылдау. Нақты жағдайлар мен оқиғалардың мүмкін болатын дамуының көп нұсқалығына, жеке тұлғаны қалыптастыруға, қиын, үнемі өзгеріп тұратын әлемде өмір сүру және жұмыс істеу қабілетіне дағдылану ықтималды - статистикалық ойлауды дамытуды талап етеді.
Мен таңдаған зерттеу тақырыбының өзектілігі комбинаторлық міндеттерді шешу кезінде, олимпиада тапсырмаларын орындауда білімді тереңдету қажеттілігінен туындап отыр.
Жұмыстың мақсаты - әртүрлі типтегі және шешу әдістері мен тәсілдерінің алуан түрлілігі кезінде комбинаторлық есептерді шешудің жалпы тәсілдерін анықтау, математиканы зерттеуге тұрақты қызығушылықты дамыту, негізгі типтегі есептерді, аралас түрдегі есептерді, күрделілігі жоғары есептерді шешу әдістерін меңгеру.
Зерттеудің негізіне комбинаторлық есептерді шешу жалпы ықтималдық теориясын түсіну мен қабылдауды жеңілдететіні туралы болжам алынған.
Қойылған мақсаттарды іске асыру және ұсынылған болжамды тексеру үшін зерттеудің келесі міндеттерін шешу қажет:
1) әдебиетті зерттеу және талдау;
2) комбинаторлық есептерді шешу тәсілдерін іздеу;
3) комбинаторлық есептерді шешу;
4) комбинаторлық есептер банкін құру.
Қойылған міндеттерді шешу барысында келесі зерттеу әдістері қолданылды:
1) Зерттеу мәселесі бойынша оқу-әдістемелік әдебиетті зерттеу және талдау;
2) салыстыру, қорыту және жіктеу әдістері;
3) теориялық-әдістемелік материалдарды жинақтау және талдау.

ІІ Зерттеу бөлімі

2.1 Комбинаториканың даму тарихы

2.1.1. Ежелгі Қытайдағы Комбинаторика
Комбинаторикаға жақын есептеулерді біздің эрамызға дейінгі XII-XIII ғасыр Ежелгі Қытай жазбаларынан кездестіреміз. Бұл қолжазбаларды дәл белгілеу мүмкін емес, өйткені б.з. б. 213 ж. император Ши Хуан-ди барлық кітаптарды (олар бамбук тақтайшаларында жазылған) өртеуге бұйрық берді, сондықтан бізге тек оларға қатысты кейінгі кітаптар ғана жетті. Бұл кітаптарда бүкіл әлемнің бастауы ер және әйел бастауларының " -- " және "- -" символдарымен белгіленген үйлесімі болып табылатыны жазылған. Қолжазбада, қазір "Өзгерістер кітабы" деген атпен белгілі, бұл белгілердің екі және екіден, үштен әр түрлі қосылыстары көрсетілген:

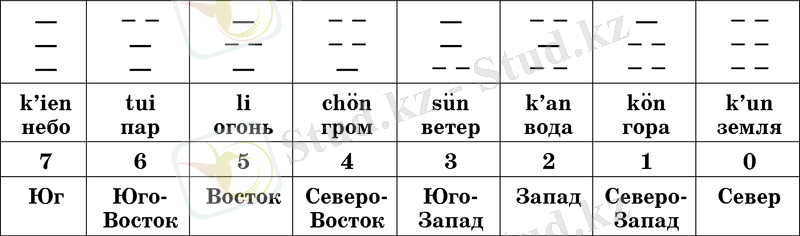
Үш қатар символдардан тұратын сегіз сурет жерді, тауды, суды, желді, найзағайды, отты, буды және аспанды бейнеледі (кейбір суреттердің өзге де мағыналары болған). Сондықтан, алғашқы 8 натурал санның қосындысы (яғни 36 саны) ежелгі қытайлықтардың көріністерінде бүкіл әлемді танытуы таңқаларлық емес. Білімнің тереңдеуіне қарай сол " -- " және " - "белгілердің көмегімен әлемнің басқа да элементтерін көрсету қажет болды. 5 қатарлы сызықтан тұратын 64 фигуралар жасалды.
Керек болса, суреттер санының екі еселенуі бірқатар белгі қосылғанда байқалды. Бұл комбинаториканың алғашқы жалпы нәтижесі ретінде қарастыруға болады. Бұл кітапта күрделі суреттер бар. Ол 2300 жыл бұрын император Ию Лошуй өзенінің жағасында қасиетті тасбақаның үстіндегі қабыршағында ақ және 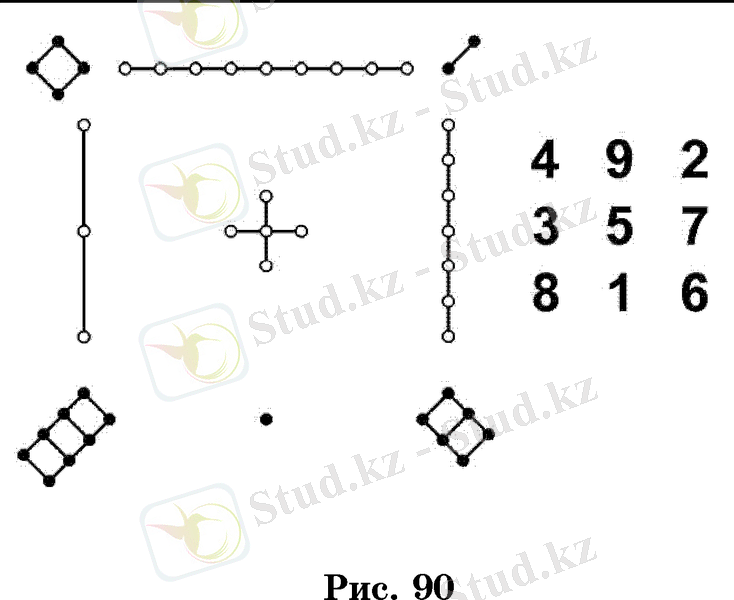қара белгілерден жасалған суретті көрді. Егер әрбір фигураны тиісті санмен ауыстырса, сол жақтағы кесте пайда болады. Әрбір жолда, бағанда және диагоналда сандарды қосу кезінде бірдей қосынды 15 саны алынады. Ежелгі қытайлықтар сандарға берген мистикалық түсіндіруде осындай керемет қасиеттері бар кестені ашу ұмытылмас әсер қалдырды.
Сурет "ло-шу" деп аталды, оны сиқырлы символ деп санады. Сондықтан, әрбір жол, баған және диагональ бойынша бірдей сомасы бар сандардың кез келген шаршы кестесін сиқырлы квадрат деп атайды.

2.1.2. Ежелгі Грециядағы комбинаторика

Б. з. б. IV ғасырда өмір сүрген Философ Ксенократ буындар санын есептеді. Б. з. б. III ғасырда Хрисипп 10 аксиомнан алынған мәлімдемелердің саны миллионнан асады деп ойлады. Гиппархтың пікірі бойынша, аксиомды бекітетін 103049 тіркесімін құрастыруға болады, ал оларға теріс 310 952 қосуға болады.
Біз осы философтардың өз тұжырымдарына қандай мағына бергенін және олар өз нәтижелерін қалай алғанын білмейміз -- Гиппарх келтірген сандар тым көп мағыналы, сондықтан оларды өрескел бағалаудың нәтижесі деп санауға болмайды, сонымен бірге олар ақылға қонымды түсіндіре алмайды. Соған қарағанда, грек ғалымдарының бізге жетпеген комбинаторлық есеп ережелері болған, олар жалған болуы да мүмкін.
Заттардың шағын тобын есептеуге қатысты нақты комбинаторлық есептерді гректер қатесіз шешті. Аристотель дұрыс үш мүшелі силлогизмдердің барлық түрлерін дәл сипаттады, ал оның шәкірті Аристоксен өлең жолдарындағы ұзын және қысқа буындардың әр түрлі комбинацияларын есептеп шықты. Б. з. IV ғасырда өмір сүрген математик Папп үш элементтен олардың қайталануына жол бере отырып, олардан алуға болатын жұптар мен үштік санын қарастырды.
Грек ғалымдары комбинаторика мен сандар теориясының арасындағы мәселелерге көп көңіл бөлді. Б. з. б. VI ғасырда философтың және математик Пифагор мектебінде әлемді сандар билейді деген тұжырым қалыптасты, ал заттар тек сандардың бейнеленуі (мүмкін, бұл идеялар вавилон мәдениетінің ықпалымен және шумерлердің ежелгі көзқарастарынан туындаған болу керек). Сондықтан әлемді тану үшін Пифагор шәкірттері натуралды сандардың қасиеттерін зерттей бастады. Олардың жұп және тақ сандар, сандар, қарапайым және құрама сандар туралы зерттеулері сандар теориясының негізін салды (ғылымда дұрыс емес бастапқы қағидалар пайдалы зерттеулерге түрткі береді).
Қытайлықтар сияқты, пифагорлықтар 36 санына ерекше мән берді - олар үшін тек алғашқы 4 жұп және бірінші 4 тақ сандар қосындысымен ғана емес, алғашқы үш кубтардың қосындысымен де болды: 36 =13+23+33 Пифагорлықтар кемелділігінің символы, мысалы, өз бөлушілерінің сомасына тең болған сандар, 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, Ал достық символы-Достық сандар, олардың әрқайсысы басқа санның бөлгіштеріне тең (мысалы, 220 және 284). 220-ның бөлгіштері 220-ны қоспағанда 1,2,4,5,10,11,20,22,44,55,110.284-т ің бөлгіштері 284-ті қоспағанда 1,2,4,71,142 . Д1=1+2+4+5+10+11+20+22+44+55+110=28 4 .
Д2 =1+2+4+71+142=220. Мұндай сандарды табу комбинаторлық өнерді талап етті.
Пифагор мектебінде тікбұрышты үшбұрыштың қабырғалары туралы теорема дәлелденген. Бұл екі квадраттың қосындысы түрінде 1, 4, 9, 16 және т.б. квадраттық сандарға қызығушылық туғызды. (сурет 2). Бірақ пифагорлықтар нүктелердің басқа конфигурацияларын қарады.
2-суреттегі әрбір үшбұрыш оның қабырғасының ұзындығы алдыңғыдан 1-ге ұлғаюынан алынады.
Әрбір үшбұрыштағы нүктелердің санын есептей отырып, 1, 3, 6, 10, үшбұрыштардың тізбегін аламыз ... Оны натуралды сандарды дәйекті түрде жинай отырып алуға болады: 1, 1 + 2, 1 + 2 + 3, 1 + 2 + 3 + 4 т.с.с.

Сур.2

Ал алтыбұрыштар 1, 5, 9 арифметикалық прогрессия мүшелерінің ішінара қосындысы ретінде алынған 1, 6, 15 алты бұрышты сандардың кезектілігіне әкеледі .
Бұдан әрі мұндай қосындыны комбинаторикада маңызды рөл атқаратын Сп кбиномиальді коэффициенттерінің көмегімен көрсете алды.
Жазықтықтан кеңістікке өту одан да күрделі сандарды құруға мүмкіндік берді. Мысалы, үшбұрыштардан пирамида жасауға болады. Мұндай пирамидалардың нүктелерінің санын есептей отырып, 1 + 3 + 6 + 10 + ... ретімен келетін пирамида сандарының, 1, 4, 10, 20 пирамидалдық сандарға келеді. Алайда, одан әрі қорытулар көп өлшемді кеңістіктерді енгізуді талап етті, бұл ежелгі грек математикасының мүмкіндіктерінің шеңберінен тыс еді.
Фигуралық сандар туралы ілім ғасырлар бойы математиктерді өзіне тартты. Олар XVII ғасырда өмір сүрген француз ғалымы Пьер Ферма айналысты, мысалы, кез келген натуралды сан үшбұрышты немесе 2 немесе 3 үшбұрышты санның сомасы; шаршы немесе 2, 3 немесе 4 квадраттың сомасы; бес бұрышты немесе 2, 3, 4 немесе 5 бес бұрышты және т.б. бар екенін дәлелдеді. Бұл теореманың кей жағдайларын Эйлер мен Лагранж дәлелдеді, ал жалпы дәлелді 1815 жылы француз математигі О. Коши берген.
Сандардың комбинаторикасымен қатар грек ғалымдары геометриялық комбинаториканың жекелеген мәселелерімен айналысты -- дұрыс және жартылай көп қырлы, ерекше түрде кесілген квадраттың 14 бөлігінен тұратын фигураларды құрастырумен және т.б. соңғы сұраққа Архимедтің "Стомахион" жұмысы арналды.
XIV ғасырдың басында тірі еврей математигі Леви бен Гершон комбинациялар санына арналған формуланы жасады.
Сnk=nn-1 ⋯ (n-k+1)1∙2∙ ⋯ ∙k
Дегенмен, ежелгі еврей тілінде жазылған оның жұмысы ғалымдардың көпшілігіне дерлік таныс болмады, бұл формуланы XVII ғасырдың басында француз математигі П. Эригон қайтадан жарыққа шығарды.
2.1.3. Шығыс елдеріндегі комбинаторика
Б. З. VIII ғасырда араб ғылымының өркендеуі басталды. Арабтар грек ғалымдарының көптеген туындыларын қайта жарыққа шығарды, оларды зерттеді, содан кейін теңдеулерді шешу, есептеу теориясы мен практикасы сияқты гректердің назарын аз аударған салаларда алға жылжыды. Кез келген дәрежедегі мәселені тамырымен шеше отырып, араб алгебраистері "Ньютон биномы" тарихи дұрыс емес атауымен белгілі екі санның сомасы дәрежесі үшін жаңа формулаға келді. Әлбетте, бұл формуланы б.з. ХІ-XII ғасырларда өмір сүрген ақын және математик Омар Хайям білген. Бұл формуланы XIII ғасырда Насир ад-Дин ат-Туси өз еңбектерінде келтіреді, ал XV ғасырда оны Гиясэддин ал-Каши зерттелген.
Араб түпнұсқаларына шығатын кейбір еуропалық деректер бойынша, осы формуланың коэффициенттерін табу үшін 10001 санын алып, оны 2-ші, 3-ші, ..., 9-ші дәрежелі. Төмендегідей кесте пайда болды.
100011 -10001
100012 - 100020001
100013 - 1000300030001
100014 - 10004000600040001
100015 - 100050010001000050001
100016 - 1000600150020001500060001
100017 - 10007002100350035002100070001
100018 - 100080028005600700056002800080001
100019 - 10009003600840126012600840036000900 01
мұнда Ньютон биномының коэффициенттері бар. Егер бұл кестеде артық нөлдерді түсіріп, жоғарыдан 100010 = 1 қоссаңыз, онда биномиалды коэффициенттерден үшбұрыш кесте болады.
Араб ғалымдары Сnk=Cn-1k+Cn-1k-1 формуласымен берілетін биномиалдардың негізгі қасиетін де білген.
Арабтармен бір мезгілде биномиалдық коэффициенттерді есептеумен қытайлық математиктер айналысты. Б. з. XIII ғасырда алгебраист Чжу Ши-дзе "Яшмовое зеркало" кітабында п = 8 сандардың да кестесін құрастырып келтірілген, . Б. з. VIII ғасырда астроном И Синь шахматты елестетін ойынның фигураларының әртүрлі орналасу қалыптарының санын есептеп шығарған.
Үндістанды да комбинация қызықтырды. Б.э. II ғасырында үнділер С санын біліп, Cn0+Cn1+⋯+Cnnсуммасы 2n.-ге тең екенін шешкен. Ал XII ғасырда үнді математигі Бхаскара "Лилавати" кітабын жазды, онда математиканың басқа мәселелерінің арасында комбинаториканың мәселелері де зерттеледі. Ол сондай-ақ орын ауыстырулар санын және бірнеше заттардың үйлесімін табу үшін ережелер берді, бұл ретте орын ауыстыруларда қайталанатын элементтер бар жағдай қарастырылады.
Liber Abaci. XII ғасырда Шығыста сауданың дамуы араб ғылымының Еуропаға енуіне алып келді. Ең батыл және білімпаз еуропалықтар арабтардың иелігінде болған Испанияға барып, онда тек грек ғалымдарының туындыларымен ғана емес, араб және үнді ғылыми ойының жетістіктерімен - алгебра және ондық санау жүйесімен танысты.
Араб оқу орындарында Алжирде сауда жасаған Пиза көпесінің ұлы Леонардо да білім алды. 1202 жылы шыққан "Liber Abaci" кітабында Фибоначчи деген лақап аты шыққан Леонардо арабтардың барлық арифметикасын, Евклид геометриясы бойынша кейбір мәліметтерді жүйеге келтірді және оларға өз зерттеулерінің нәтижелерін қосты. Фибоначчаның еңбегі жаңа комбинаторлық тапсырмаларды, мысалы, 1-ден 40 фунтқа дейін кез келген салмақты алуға болатын гирьдің ең аз санын табу туралы. Леонардо және теңдеулердің бүтін шешімін табу да қарастырды. Одан әрі ұқсас есептер комбинаториканың тарауларының бірі ретінде қарастырылуы мүмкін теңдеулер мен теңсіздіктер жүйелерінің табиғи шешімдерінің санын табуға әкелді.
Бірақ Леонардоның комбинаторика алдындағы басты еңбегі - қояндар туралы тапсырманы қалыптастырғаны және шешкен. Грек математиктері заманынан бастап реттілігі белгілі болғаны - олардың әрбір мүшесі алдыңғы арифметикалық және геометриялық прогрессияның ережелерден алынған. Леонардо есебінде жаңа реттілік пайда болды, оның мүшелері бір-бірімен Сn=Cn-1+Cn-2арақатынасымен байланысты болды. Бұл ғылым тарихындағы алғашқы формула болды, мұнда келесі мүше алдыңғы екі мүше арқылы анықталады. Мұндай формулалар рекуррентті деп аталды (латын recurrere-қайта оралу). Рекуррентті формулалар әдісі кейіннен комбинаторлық есептерді шешу үшін ең оңтайлысы болып шықты.
Сүйек ойыны
Комбинаториканың дамуына құмар ойындар айтарлықтай серпін берді. Сүйектегі ойын ең көп таралғаны - екі немесе үш кубик, ұпай саны жазылған кубиктерді үстелге лақтырып, қайсында көп сан болса, сол көп ұпай жинаған.
Мұсылман ғалымдары кубик лақтыра отырып сүйектерді қозғайтын, нарды ойыны туралы жазған.
Тәжірибелі ойыншылар, сүйектерді лақтырып жаттығып, кейбір ұпайлар жиі түсіп жатқанын байқады, ал басқалары -- сирек. "Азарт" сөзі араб "азардан" шыққан -- қиын, сирек кездесетін сүйектердің комбинациясы деп аталады. Бұл жерде қалай жасалғанын түсінуге тырысып, қанша жолмен қандай ұпай, қандай да бір санын алуға болатын кестелерді құрастырды. Кейде қателіктер жіберілген, біріншіден, осы қосындыны берген сүйектердің әртүрлі үйлесімдерінің санын ғана есептеді.
Мысалы, екі сүйекті тастағанда 6 = 1+5, 2+4 және 3+3 ретінде, 7 сомасы 1+6, 2+5 және 3+4 комбинацияларынан, ал 8=2+6, 3+5 және 4+4 комбинацияларынан алынады.Әр жолы осы сомамен үш түрлі үйлесім болғандықтан, 6, 7 және 8 ұпайларының сомасы бірдей жиі түсуі керек деген қате қорытынды жасалады . Бірақ бұл тәжірибеге қайшы келді - 7 ұпай жиі түсті. Себебі, 3+3 комбинациясының екі сүйегін тастағанда тек қана, ал 3+4 комбинациясында -- екі тәсілмен (3+4 және 4+3) алынуы мүмкін.Бұл 7 сомасының көп түсу жиілігі түсіндіріледі. Осылайша, ұпайлардың үйлесімін ғана емес, олардың тәртібін де ескеру керек болды.
Мұнда үш сүйекке қатысты зерттеулер күрделі болды. Мұнда сүйектер тәртібін есепке алу кезінде 3 6 =216 түрлі комбинация, ал тәртіпті есепке алмағанда -- 56 ғана көрсетіледі.
Осы сұрақтармен XVI ғасырдың д. Кардано, Н. Тарталья және т. б. сияқты белгілі итальян математиктері айналысты.
Оны XVII барынша зерттеген Галилео Галилей, бірақ оның жазбалары 1718 жылға дейін жарық көрмеді.
Ойыншы және ғалымдар
XVII ғасырда сүйектегі ең құмар ойыншылардың бірі жарыстың жаңа түрлерін үздіксіз ойлап тапқан шевалье де Мере болды. Мысалы, ол төрт сүйекті лақтырып, олардың ең болмағанда біреуі алтыда ашылған жағдайда ғана ұтысқа ие болады деп ұсынды. Алайда, көп ұзамай оның серіктестері мұндай ойынға қатысудан бас тартты -- шевалье жеңілістен гөрі жиі жеңіске жеткен еді. Содан кейін де жаңа жобаны ойлап тапты -- ол бірнеше рет сүйектерді лақтырып, екі алты рет түсіп қалса ұтысты болды. Ойын біріншідегідей сияқты тиімді болу үшін қанша лақтыру керек екенін анықтау керек болды. Шевалье сүйектерді 24 рет лақтыру керек деп шешті. Өйткені, бір сүйектің төрт рет тастағанда жартысынан көбі алтылық болған, ал екінші сүйек құлаудың алты нұсқасын бергенде 4-ті 6-ға көбейту керек. Ой-пікір мінсіз көрінген, бірақ бұл тәжірибе де үмітті растамады -- енді Мере жеңіске қарағанда жиі ұтыла бастады.
Енді ставкаларды бөлу туралы мәселе туындады. Мәселе мынадай болды: Ойын алты жеңіске дейін жүреді; бір ойыншы 5 партияны, ал екіншісі -- 4 жеңіп алған кезде ойын тоқтатылды; ставканы қалай бөлуге болады? 5:4-қатынасында бқлініс сәтсіз екені анық болды.
Де Мере шамада Францияның XVII ғасырдағы екі ірі математиктері - Блез Паскаль мен Пьер Фермадан түсіндірулерін сұрады. Олардың алдына қойылған осы және басқа да мәселелерді талдай отырып, олар комбинаториканың және ықтималдықтар теориясының алғашқы теоремаларын тұжырымдады және дәлелдеді. Ал ставканы бөлу туралы мәселені Паскаль бір ойыншы ойын бітуіне r партия, ал екінші s партия қалған жағдайға жалпылама әкеліп шешті. Есептің тағы бір шешімін Ферма берді.

2. 2 Математиканың жаңа тармағы

Паскаль мен Ферма жұмысы математика ғылымның екі жаңа тармағының - комбинаториканың және ықтималдықтар теориясының тууына жол ашты. Егер оларға дейін комбинатоикалық мәселелер астрология, логика және математика бойынша жалпы еңбектерде ғана қозғалса, сондай-ақ көбінесе математикалық ойын-сауық саласына қатысты болса, онда 1666 ж. Готфрид Вильгельм Лейбниц Комбинаторлық өнер туралы диссертациясын жариялайды.
Лейбництің диссертациясы өзінің хаттары мен баспа еңбектерінде жиі айтылған үлкен жұмыстың басы ғана болуы керек еді және ол туралы кітапшаларында көптеген жазбалар жасаған. Олардың ішінде Лейбниц комбинаторикаға үнемі жаңа ұсынымдар (кодтау және ойындарға, статистикаға, бақылау теорияларына) жасағанын көруге болады. Лейбниц комбинаториясы дегеніміз қазіргі дискретті математика деп айтым жүргеніміз болып табылады. Лейбниц комбинаторикасының аймағына "әмбебап сипаттаманы" -- яғни қазіргі математикалық логиканың түсінігін жатқызады.
Лейбництің жобалары оның заманының ақыл-ойлы математиктеріне ұқсамайтын болып көрінді, бірақ компьютерлерді жасағаннан кейін Лейбництің көптеген жоспарлары өмірге бейімделе бастады, ал Дискретті математика классикалық математикалық талдаумен бәсекелесе бастады.
1713 жылы Якоб Бернуллидің немересі Николай Якоб Бернуллидің "Ars conjectandi" ("Жорамалдар өнері") кітабының II бөлімінде п элементінен k элементіне ауысу үшін формулалар өрнектерін көрсетті. Ғылым академиясы. Комбинаторика саласындағы үлкен жетістіктер XVIII ғасырдағы швейцарлық ұлы математик Леонард Эйле - рге тиісті. Ол бүкіл өмірін Ресейде өткізген Петербург ғылым академиясының мүшесі болған. Эйлердің ғылым саласындағы негізгі жұмыстары математикалық талдауға арналған, осы және басқа да бағыттарда зерттеулер жасап, ғылымға үлкен жол салып кетті.
Бірақ Эйлер оның назарын аудармайтын-ақ мәселелерге уақыт бөлді; мәселен, Кенигсбергтегі (қазіргі Калининград) көпірлерді бір көпірге екі рет келмеу үшін айналып өтуге болады ма; әр қатарда және әр лекте әр полктен әрбір әскери атақтың бір офицері болатындай 6 түрлі полктен 36 офицер қоюға бола ма?; бұл санды қанша жолмен бөлуге болады және т.б. бұл әдісбастапқыда оғаш көрінгенімен, көпірлер туралы есептеулер кейін топология мен графтар теориясы, офицерлер туралы қазіргі эксперименттерді жоспарлауға азық болды, ал сандарды бөлу туралы есепті шешу кезінде қолданылған әдістер ұзақ және күрделі даму жолынан кейін математикалық физика теңдеулерін шешу үшін қолданылатын интегралдық түрлендірулер туралы ғылымға айналды.
Паскаль мен Ферма, Лейбница және Эйлер жұмыстарынан кейін комбинаторика туралы ықтималдықтар теориясы, қатарлар және басқа да көптеген ғылым салаларымен тығыз байланысты математиканың дербес тармағы ретінде қарастыруға болады. XVIII ғасырдың соңында неміс ғалымы Гинденбург және оның оқушылары комбинаторлық талдаудың ортақ теориясын құруға талпыныс жасады. Алайда, ол табысқа жете алмады -- сол кезде мұндай теория үшін қажетті іргетас бере алатын маңызды және қызықты міндеттердің жеткілікті саны жинақталмады.
XIX ғасырда комбинаторика бойынша зерттеулер барысында осы теорияның анықтаушылармен, соңғы геометриялармен, топтармен, математикалық логикамен және т. б. байланысы байқалады.

2.3. Комбинаториканың түрлеріне есептер шығару
Комбинаторлық есептердің шарты
Егер оның шешімі кейбір соңғы жиын элементтерін таңдау болса, тапсырманы комбинатор деп атауға болады.
Комбинаторлық тапсырмалардың ерекше белгісі-ол мынадай сөзбен басталатын болу керек:
Қанша жолмен... Қанша нұсқа...
Комбинаторика бойынша тапсырманы шешу үшін алдымен оның мағынасын түсіну керек, яғни тапсырмада сипатталған ойлы процесс немесе әрекетті ұсыну керек.
Есептегі қосылыстардың түрін нақты анықтау керек, ал ол үшін бірнеше түрлі комбинацияларды құрап, элементтер қайталанатынын, олардың құрамы өзгере ме, элементтер тәртібі маңызды ма, соны тексеру керек.
Егер комбинаторлық есеп қосылымдарға салынатын бірқатар шектеулерден тұрса, онда бұл шектеулердің қосылыстарға қалай әсер ететінін немесе әсер етпейтінін түсіну қажет.
Егер тапсырманың қандай да бір маңызды сәттерін бірден анықтау қиын болған жағдайда, мысалы, бастапқы тапсырмада немесе элементтердің аз саны қарастырылатын тапсырма бар болса, шектеулер ескерілмейтін болса, онда таңдаулардың пайда болу принципін түсіну оңайырақ болады. Комбинаторлық тапсырма қарапайым есептердің әр түрлі комбинацияларынан құралса, онда тапсырманы қосымша беруге бөлу керек.
Орналастыру. п объектілер бар болсын, олардың барлығы бір-бірімен ажыратылады:Алмастырулар - әртүрлі n элементтердің тек орналасу тәртібімен ғана ерекшеленетін комбинациялар.
Олар: кітаптар, балалар текшелері немесе крыловтың "квартетінің" музыканттары. Оларды қатарға оймен орналастырамыз және нысандардың осындай реттелген орналасуын ауыстырып қою деп атаймыз. Сұрақ қоюға тырысамыз: п заттардан қанша ауысу мүмкін? Ауыстырулар саны Рп,-мен белгіленеді, сол арқылы ол заттардың санына байланысты екенін білдіреді.
Элементтен жасалған алмастырулар санын Рn үшін мынадай формула қолданады: және алмастырулар санын есептеп белгілейді. Рn=n! (1)Мұндағы n!=1x2x3x...xn.
Алдымен аздаған п үшін Рп тауып көрейік. Егер п = 1 болса, яғни бір ғана зат бар, онда оны орналастырудың бір ғана жолы бар. Сондықтан Р1 = 1. Енді п = 2 алсақ, Р2 = 2 екені анық, себебі екі затты (оларды А және Б атайық). Екі түрлі жолмен қоюға болады: АБ және БА. Бірнеше басқаша пайымдауға тырысамыз: бірінші затты (А) қозғалыссыз орнатамыз, ал екіншісін (Б) оған ыңғайластырамыз. Әрине, Б объектісін А объектісінен алдынан немесе артынан қоюға болады, демек, Р2 орнын ауыстыру саны Р1 қарағанда екі есе көп , яғни . Р = Р1 ::2 = 1 :: 2. Енді үшінші В затты қосамыз. А және Б екі нысанның әр орнына үшінші затты үш түрлі жолмен жапсыра салуға болады: оның алдынан, арасына немесе артына қою. АБ орнын ауыстыру, осылайша үш орнын ауыстырады: ВАБ, АВБ және АБВ, БА орнын ауыстыру -- үш: ВБА, БВА және БАВ, және барлық пайда болған алты орнын ауыстыру -- әр түрлі. Мұнда Р3 = P2 :: 3 = 1 :: 2 :: 3 шығады.
Жалпы, n - 1 заттардың әрбір орнын ауыстырудан n қосымша орын ауыстыруларды алуға болады, n-ші затты алдына немесе артына не заттар арасында (п - 1 заттардың арасында п - 2 аралық бар; 1 + 1+n-2 -- міне, n дәл шығады). n-1-ден n пәндерге көшкен кезде ауыстырулар саны n есе артады. Сондықтан жалпы формула мынадай болады: Pn=1∙2∙3∙...∙n=n!.
п - 1 заттардың әрбір орнын ауыстырудан п -затты немесе алдыңғы немесе артынан, немесе заттар арасына қосып, п -затты ауыстыра отырып, п - 1 заттарды алуға болады.
Леп белгісі (математикада ол факториал деп аталады) 1-ден n-ге дейінгі барлық натуралды сандардың ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.