Оқушылардың тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдыларын қалыптастыруға бағытталған техниканы жасау

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

Қазіргі уақытта мектептегі білім беруді қайта құрудың негізгі міндеті-оқытудың дамып келе жатқан функциясының басымдығына қайта бағдарлау. Бұл дегеніміз, тұлғаның интеллектуалды дамуы, яғни оқу-танымдық іс-әрекетті дамыту міндеті бірінші орынға шығады. Мүмкін, бірде-бір мектеп пәні ойлау тұлғасын тәрбиелеудегі математиканың мүмкіндіктерімен бәсекелесе алмайды.
Бірнеше онжылдықтар бойы тригонометрия мектептегі математика курсының жеке пәні ретінде жоқ, ол тек негізгі мектептің геометриясы мен алгебрасына ғана емес, алгебра мен талдаудың басталуына да қатысты.
Тарихи тұрғыдан алғанда, мектеп курсында Тригонометриялық теңдеулер мен теңсіздіктер ерекше орын алды. Тағы гректер тұсында, адамзат қиямет тригонометрия маңызды ғылым. Сондықтан біз ежелгі гректермен дауласпай, тригонометрияны мектеп курсының және жалпы математика ғылымының маңызды бөлімдерінің бірі деп санаймыз.
Тригонометриялық теңдеулер мен теңсіздіктер орта мектептің математика курсында оқу материалының мазмұны бойынша да, оқу-танымдық іс-әрекет әдістері бойынша да орталық орындардың бірін алады, оларды оқу кезінде құрылуы мүмкін және жасалуы керек және теориялық және қолданбалы сипаттағы көптеген мәселелерді шешуге қолданылады.
Мектептегі математикалық білім беруде бірнеше бағыттар Тригонометриялық теңдеулер мен теңсіздіктерді зерттеумен байланысты:
1. Теңдеулер мен теңсіздіктерді шешу;
2. Теңдеулер мен теңсіздіктер жүйесін шешу;
3. Теңсіздіктердің дәлелі.
Оқу, ғылыми-әдістемелік әдебиеттерді талдау
бірінші және екінші бағыттарға көп көңіл бөлінеді.
Біздің заманымыздың талабы-математиканы оқытуда қолданбалы бағыттарды күшейту қажеттілігі. Мектептегі математикалық білімнің мазмұнын талдау көрсеткендей, тригонометриялық теңдеулерді, әсіресе тригонометриялық теңсіздіктерді шешу мүмкіндіктері өте кең.
Сондай-ақ, Тригонометриялық теңдеулер мен теңсіздіктерді шешу тригонометрия бойынша барлық оқу материалдарымен байланысты студенттердің білімін жүйелеуге алғышарттар жасайтындығын (мысалы, тригонометриялық функциялардың қасиеттері, тригонометриялық өрнектерді түрлендіру әдістері және т. б.) және алгебра бойынша зерттелген материалмен тиімді байланыс орнатуға мүмкіндік беретінін атап өткен жөн (теңдеулер, теңдеулердің теңдігі, теңсіздіктер, бірдей түрлендірулер). алгебралық өрнектер және т.б.).[1]
Басқаша айтқанда, Тригонометриялық теңдеулер мен теңсіздіктерді шешу әдістерін қарастыру осы дағдыларды жаңа мазмұнға ауыстыруды қамтиды.
Зерттеудің өзектілігі: әр түрлі авторлардың 10-11 сыныптары үшін "Алгебра және талдаудың басталуы" оқу құралдарындағы Тригонометриялық теңдеулер мен теңсіздіктерді шешуге арналған материалды талдау, Тригонометриялық теңдеулер мен теңсіздіктерді зерттеу мақсаттарын, сондай-ақ тақырыпқа байланысты оқытудың міндетті нәтижелерін ескеру мұғалімнің алдында тұрған міндет екенін көрсетеді. оқушылар әр түрдің теңдеулері мен теңсіздіктерін шеше алады, осылайша жалпы тригонометриялық идеяларды дамытады.
Зерттеудің мақсаты: оқушылардың Тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдыларын қалыптастыруға бағытталған техниканы жасау.
Зерттеу нысаны: Математиканы оқыту процесі.
Зерттеу пәні: оқушылардың Тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдыларын қалыптастыру әдістемесі.
Зерттеу гипотезасы: егер біз Тригонометриялық теңдеулер мен теңсіздіктерді шешуде қажетті негізгі дағдыларды бөліп алып, оларды қалыптастыру әдістемесін жасасақ, онда бұл Тригонометриялық теңдеулер мен теңсіздіктерді шешуге сапалы оқытуға ықпал етеді.
Тригонометрияны саналы және сапалы зерттеу арқылы біз жеке тұлғаға бағытталған оқыту идеяларын ескере отырып жүзеге асырылатын оқу процесін түсінеміз, оны жүзеге асыру кезінде білімді формальды түрде беруге және дағдыларды схоластикалық өңдеуге жол берілмейді, яғни тригонометрияны зерттеу ойлаудың логикалық және бейнелі компоненттеріне негізделуі керек, ал студенттерге саралау және даралау үшін мүмкіндіктер берілуі керек.
Зерттеу және гипотезаның дұрыстығын тексеру барысында келесі мәселелерді шешу қажет болды:
1. Зерттеу мәселесі бойынша психологиялық-педагогикалық, оқу және әдістемелік әдебиеттерге талдау жасау.
2. Математиканы оқытудағы Тригонометриялық теңдеулер мен теңсіздіктердің рөлін анықтаңыз.
3. Тригонометриялық теңдеулер мен теңсіздіктерді шешу үшін қажетті дағдыларды қалыптастыру негіздерін таңдаңыз.
4. Тригонометриялық теңдеулер мен теңсіздіктерді шешу әдістерін жіктеу.
5. Тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдыларын қалыптастыру әдістемесін жасау.
6. Әзірленген Әдістемеге эксперименттік зерттеу жүргізу.
Қойылған міндеттерді шешу үшін келесі зерттеу әдістері қолданылды:
1. Психологиялық-педагогикалық және әдістемелік әдебиеттерді талдау.
2. Оқу-әдістемелік құралдарды, оқулықтарды, дидактикалық материалдарды талдау.
3. Бақылау, мұғалімдермен әңгімелесу.
4. Педагогикалық эксперимент.

Тригонометрияның ғылым ретінде даму кезеңдері

Тригонометрия-бұл XVIII ғасырда ғана соңғы дизайнды алған қарапайым математиканың ең жас бөлімдерінің бірі, дегенмен оның жеке идеялары ежелгі дәуірге, ежелгі әлемге және үндістердің математикалық шығармашылығына жатады (к.Птолемей, II ғасыр, Аль Баттани, IX ғасыр, және т. б.). Еуропалық математиктер табиғи синустар мен тангенс кестелерін есептеуде жоғары деңгейге жетті (Региомонтанус, XV ғасыр, Ретикус және Питискус, XVI ғасыр және т.б.).
"Үшбұрыштарды өлшеу" дегенді білдіретін грек тектес "тригонометрия" атауының өзі: (тригонон) - Үшбұрыш, (метрейн) - өлшеу.
Тригонометрияның ғылыми дамуын Л.Эйлер өзінің "Jntroductio in analysis infinitorum" (1748) еңбегінде жүзеге асырды. Ол тригонометрияны функциялар туралы ғылым ретінде құрды, оған аналитикалық мәлімдеме берді, формулалардың барлық жиынтығын бірнеше негізгі формулалардан шығарды. Тараптарды кіші әріптермен және қарама -- қарсы бұрыштармен-тиісті үлкен әріптермен белгілеу оған барлық формулаларды жеңілдетуге, оларға айқындық пен үйлесімділікті енгізуге мүмкіндік берді. Эйлер тригонометриялық функцияларды тиісті сызықтардың шеңбер радиусына қатынасы ретінде қарастыру идеясына ие, яғни. сандар ретінде және шеңбердің радиусы" толық синус " ретінде ол бірлік ретінде қабылданды. Эйлер бірқатар жаңа қатынастарға ие болды, тригонометриялық функциялардың экспоненциалды байланысын орнатты, барлық тоқсандарға функция белгілерінің ережесін берді, жалпыланған индукция формуласын алды және тригонометрияны барлық еуропалық математика оқулықтарында жіберілген көптеген қателіктерден босатты.
Л. Эйлердің шығармасы кейіннен тригонометрия оқулықтарының негізі болды. Алғашқы нұсқаулықтардың бірі, С.Румовскийдің "қысқартылған математика" (1760), "жазық тригонометрияның бастапқы негіздері" бөлімі презентацияны келесідей бастайды: "жазық Тригонометрия-бұл арифметикалық есептеулер арқылы геометрия тапқан үшбұрыштарды табу". Барлық презентация үшбұрыштарды шешуге дейін азаяды (қарапайым жағдайлар), есептеулер өте күрделі түрде жүргізіледі, функциялар туралы ілім жоқ.
Осылайша, тригонометрия геометриялық негізде пайда болды, геометриялық тілге ие болды және геометриялық есептерді шешуге қолданылды. Алгебралық символизмнің дамуы тригонометриялық қатынастарды формулалар түрінде жазуға мүмкіндік берді; теріс сандарды қолдану бағытталған бұрыштар мен доғаларды қарастыруға және тригонометриялық сызықтар ұғымын (шеңбердегі белгілі бір сегменттер) кез-келген бұрышқа таратуға мүмкіндік берді. Осы кезеңде тригонометриялық функцияларды сандық аргумент функциялары ретінде зерттеу үшін негіз, тригонометриялық (дөңгелек) функциялардың аналитикалық теориясының негізі құрылды. Тригонометриялық функциялардың мәндерін кез-келген дәлдік деңгейімен есептеуге мүмкіндік беретін аналитикалық аппаратты Ньютон жасаған.[25]
Тригонометрияның заманауи түрі ұлы ғалым, Ресей Ғылым академиясының мүшесі Л.Эйлердің (1707 - 1783) еңбектерінде алынған. Эйлер тригонометриялық функциялардың мәндерін Сан ретінде қарастыра бастады - радиусы бірлік ретінде қабылданған шеңбердегі тригонометриялық сызықтардың шамалары ("тригонометриялық шеңбер" немесе "бірлік шеңбер"). Эйлер әр түрлі кварталдардағы тригонометриялық функциялардың белгілері туралы түпкілікті шешім қабылдады, барлық тригонометриялық формулаларды бірнеше негізгі формулалардан шығарды, оған бірнеше белгісіз формулаларды орнатты, біркелкі белгілерді енгізді. Оның жазбаларында жазбалар алғаш рет кездеседі . Ол сонымен қатар күрделі аргументтен тригонометриялық және экспоненциалды функциялар арасындағы байланысты ашты. Л. Эйлердің еңбектері негізінде тригонометрия оқулықтары құрастырылды, оны қатаң ғылыми дәйектілікпен ұсынды.
Эйлер бастаған тригонометриялық функциялар теориясының аналитикалық (геометрияға тәуелді емес) құрылысы ұлы орыс ғалымы Н.И. Лобачевскийдің еңбектерінде аяқталды.
Тригонометриялық функцияларға сандық дәлел функциясы ретінде қазіргі көзқарас негізінен физика, механика, техниканың дамуына байланысты. Бұл функциялар математикалық аппараттың негізін құрады, оның көмегімен әртүрлі мерзімді процестер зерттеледі: тербелмелі қозғалыстар, толқындардың таралуы, механизмдердің қозғалысы, ауыспалы электр тогының тербелісі. Ж.Фурье (1768 - 1830) көрсеткендей, кез-келген дәлдік дәрежесі бар кез-келген периодты қозғалыс қарапайым синусоидалы (гармоникалық) тербелістердің қосындысы түрінде ұсынылуы мүмкін. Егер тригонометрияның дамуының басында қатынас тек гипотенузасы 1-ге тең ауыспалы тік бұрышты үшбұрыштың жақтарында салынған квадраттардың аудандары арасындағы байланысты білдірсе, онда кейіннен бұл қатынас осы кедергі болатын екі тербелмелі қозғалыстың қосылуын да көрсете бастады.
Осылайша, оның дамуының бастапқы кезеңдерінде тригонометрия есептеу геометриялық есептерін шешудің құралы болды. Оның мазмұны қарапайым геометриялық фигуралардың, яғни үшбұрыштардың элементтерін есептеу болып саналды. Бірақ қазіргі тригонометрияда тәуелсіз және тригонометриялық функциялардың қасиеттерін зерттеу бірдей маңызды. Тригонометрияның дамуының бұл кезеңі тербелмелі қозғалыстар механикасының, дыбыстық, жарық және электромагниттік толқындар физикасының барлық даму жолымен дайындалды.
Осы кезеңде тригонометрияның көптеген терминдеріне жалпылау беріледі, атап айтқанда , n - натурал сан және басқа функциялар үшін қатынастар алынады және қазір қуат қатарларының қосындысы ретінде қарастырылады:

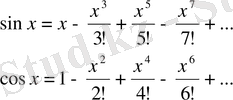
В.Никитин мен П. Суворовтың оқулығы да дерлік баяндалған.
Тригонометрияның толық ғылыми тұжырымы акад береді. М. Е. Головин өзінің "алгебралық дәлелдермен жалпақ және сфералық тригонометрия" оқулығында, 1789. Бұл кітапта сіз тригонометрияның барлық маңызды формулаларын XIX ғасырда оларды сипаттау әдеттегідей таба аласыз. (кері тригонометриялық функцияларды қоспағанда). Автор презентацияны секанс пен косеканс енгізумен шатастырудың қажеті жоқ деп тапты, өйткені бұл функциялар сирек жағдайларда іс жүзінде қолданылады.
1804 жылы Н. Фусстың оқулығы жарық көрді. Кітап гимназияларға арналған. "Жазық тригонометрия, -- дейді автор, - үш мәліметтен тұратын және тік бұрышты үшбұрыштың бейнеленген бөліктерінің сандары оның басқа үш бөлігін анықтайтын ғылым бар". Оқулық 4 тең бөліктен тұрады. Жалпы ұғымдар, үшбұрыштардың шешімі, практикалық геометрия мен геодезияға тригонометрияны қолдану және соңында қосу теоремасы. Н. Фусстың оқулығы сфералық тригонометриядан бөлінген.
1851 жылы академик М. в. Остроградский әскери-оқу орындарында басшылық жасау үшін тригонометрия туралы жазбасында ол тригонометриялық функцияларды анықтаудың жақтаушысы ретінде әрекет етеді, оларды зерттеудің бірінші кезеңінде тікбұрышты үшбұрыштағы тараптардың қарым-қатынасы ретінде, содан кейін олардың анықтамасын жалпылап, оны кез-келген мөлшердегі бұрыштарға таратады. [24]

Әр түрлі мектеп оқулықтарындағы тригонометрия материалдарының мазмұны мен талдауы

Тригонометриялық теңдеулер мен теңсіздіктерді шешуге арналған материалды талдау, а.н. Колмогоров өңдеген 10-11 сыныптарға арналған "Алгебра және талдаудың басталуы" оқулығында және авторлар ш. а. Алимов және т. б. 10-11 сыныптарға арналған "Алгебра және талдаудың басталуы" оқулығында Тригонометриялық теңдеулер мен теңсіздіктердің әртүрлі түрлері математика оқулықтарында ұсынылған. орта мектеп. Ендеше, мұғалім алдында міндет - оқушылардың іскерлігі шешу теңдеулер мен теңсіздіктер әрбір түрі.
Осы тақырыпты мектеп математика курсында енгізудің ең қолайлы әдісін салыстыру, талдау және қалыптастыру мақсатында орта мектептің 10-11 сыныптарындағы математика бойынша әртүрлі оқулықтарда келтірілген тригонометрия материалының мазмұнын қарастырыңыз.
Башмаков м. и. Алгебра және талдаудың басталуы. 10-11
Оқулық 6 тарауға бөлінген. Әр тарау сұрақтар мен тапсырмалар тізімімен ашылады. Содан кейін тарауды зерттегеннен кейін қол жеткізуге болатын нәтижелер қысқаша тұжырымдалады. "Тригонометриялық теңдеулер мен теңсіздіктерді шешу" тақырыбына қатысты Материал "функциялар мен графиктер" және "туынды және оны қолдану" тарауларын зерттегеннен кейін "Тригонометриялық функциялар"III тарауында келтірілген.
Төртінші тарау "экспоненциалды және логарифмдік функциялар "және Бесінші тарау" Интеграл және оны қолдану "тригонометрия саласына қатысты үндеулерді қамтымайды, ал алтыншы тарауда" теңдеулер мен теңсіздіктер " Тригонометриялық теңдеулер де, тригонометриялық теңсіздіктер де кездеседі.
III тарауда "Тригонометриялық функциялар" тақырыбына сілтеме жасай отырып, М.и. Башмаков келесі тақырыптарды қайталау қажет деп санайды: бұрыштарды өлшеу; үшбұрыштағы қатынастар; айналмалы қозғалыс; есептеу техникасы. Әрі қарай: тригонометриялық функциялардың анықтамалары мен қарапайым қасиеттері; азайту формулалары; тригонометриялық функциялардың мәндері.
Сонымен қатар, мұнда негізгі тригонометриялық сәйкестік енгізіледі.
Мұнда М. және Башмаков тригонометриялық шеңбер бойымен қарапайым тригонометриялық теңдеулерді шешу мәселесін қарастырады.
Осы тақырыптың келесі бөлімдері "тригонометриялық функцияларды зерттеу"және" бірдей түрлендіру". Осыдан кейін "теңдеулер мен теңсіздіктерді шешу" бөлімінде әр түрлі теңдеулер мен теңсіздіктердің кейбір түрлері енгізіледі. Тиісінше, мұнда оларды шешудің әдістері мен әдістері туралы айтылады.
"Тригонометриялық теңдеулер мен теңсіздіктерді шешу" тақырыбын зерттеу схемасы келесідей анықталады: функция -- теңдеулер -- түрлендірулер.[3]
Мордкович А. Г. Алгебра және талдаудың басталуы. 10-11
Оқулық 8 тарауға бөлінген. Әр тарауды зерттеудің соңында зерттеудің негізгі нәтижелері нақты көрсетілген. 10-сыныпта математиканы оқу курсы "Тригонометриялық функциялар"тарауын зерттеуден басталады. Мұнда автор координаталық жазықтықтағы тригонометриялық шеңбер ұғымдарын, синус пен косинус ұғымдарын, олармен байланысты негізгі тригонометриялық қатынастарды, тригонометриялық шеңбер бойымен қарапайым теңдеулердің шешімдерін енгізеді. Осылайша, индукция формулалары бұрыштық Аргументтің тригонометриялық функцияларын зерттегеннен кейін енгізіледі. Әрі қарай тригонометриялық функциялардың қасиеттері мен графиктері қарастырылады. "Тригонометриялық теңдеулер" екінші тарауында арксинус, арккосинус, арктангенс бұрын енгізілген ұғымдарға негізделген әр қарапайым тригонометриялық теңдеудің шешімі егжей-тегжейлі қарастырылады. Сол тарауда шешудің келесі әдістері қарастырылған: факторизация және жаңа айнымалыны енгізу; біртекті тригонометриялық теңдеулерді шешу әдісі. Шешудің басқа әдістері "тригонометриялық өрнектерді түрлендіру"үшінші тарауын зерттегеннен кейін қарастырылады.
Мұнда оқу схемасы келесідей: функция -- теңдеулер -- түрлендірулер.
Қолдану тұрғысынан мордковичтің оқулығы студенттердің өз бетінше оқуы үшін ыңғайлы, өйткені оның құрамында күшті теориялық негіз бар. Теориялық материалды ұсыну өте егжей-тегжейлі. Сыныпта сабақ өткізуге арналған сағаттардың жетіспеушілігі жағдайында оқушылардың кітаппен өзіндік жұмысының маңызы артады. Оқулыққа сүйене отырып, мұғалім сабақта оқушыларға не айту керектігін, оларды не есте сақтау керектігін және үйде оқуға не ұсынуға болатындығын жақсы біледі.
Кемшіліктерге оқулықтың өзінде осы тақырып бойынша өте көп жаттығулар кірмейді.[19]
Колмогоров а. н. Алгебра және талдаудың басталуы
Оқулықта 4 тарау бар. "Тригонометриялық теңдеулер мен теңсіздіктерді шешу" тақырыбындағы материалды зерттеу схемасы бұрынғыдан түбегейлі ерекшеленеді, өйткені алдымен сандық Аргументтің тригонометриялық функциялары және тригонометрияның негізгі формулалары қарастырылады. Сол бірінші тарауда, бірақ сәл кейінірек тригонометриялық функциялардың негізгі қасиеттері, олардың графикасы және оларды зерттеу қарастырылады. Осыдан кейін арксинус, арккосинус, арктангенс, арккотангенс және қарапайым Тригонометриялық теңдеулер мен теңсіздіктерді шешуге "параллель" ұғымдар енгізіледі. Автор тригонометриялық теңдеулерді шешу әдістерін атамайды, бірақ оларды шешу алгоритмін сипаттайды. Тригонометриялық теңсіздіктерді шешуге де қатысты.
Сонымен, зерттеу схемасы келесідей: түрлендіру -- функциялар -- теңдеулер.
Айта кету керек, оқулықта қарапайым және күрделі көптеген дидактикалық материалдар бар. Бұл, әрине, мұғалімге студенттерге арналған тапсырмаларды өзгертуге мүмкіндік береді.
Теориялық материалды ұсыну тұрғысынан оқулық өзін-өзі зерттеу үшін өте қолайлы деп айтуға болмайды.[14]
"Тригонометриялық теңдеулер" тақырыбындағы тапсырмалар жиынтығының мазмұнын талдау келесі тұжырымдарға әкеледі:
1) Қарапайым Тригонометриялық теңдеулер басым, олардың шешімі арксинус, арккосинус, арктангенс ұғымдарындағы тиісті функциялардың анықтамаларына негізделген;
2) Тригонометриялық теңдеулер іс жүзінде жоқ, оларды шешу әдісі шектеулі синус пен косинус қасиетіне негізделген;
3) Егер тригонометриялық теңдеулерді шешу әдістерінің тригонометриялық және алгебралық өрнектерді бірдей түрлендіру әдістерімен байланысы туралы айтатын болсақ, онда оқу құралындағы бұл әдістер нашар және біркелкі ұсынылғанын атап өткен жөн. Бірдей қайта құру әдістері қарастырылады:
а) тригонометриялық өрнектер:
- негізгі тригонометриялық сәйкестікті пайдалану әдісі;
- қабылдау формулаларды пайдалану қосарланған және жартылай дәлелдер;
- тригонометриялық өрнектердің қосындысын көбейтіндіге түрлендіру әдісі;
б) алгебралық өрнектер:
- көбейткіштерге жіктеуді қабылдау;
- қабылдау, түрлендіру тригонометрического білдіру білдіретін біркелкі многочлен қатысты синуса және косинуса.
Бұл әдістерді қолдану тригонометриялық теңдеулерге әкеледі, оларды шартты түрде келесі түрлерге бөлуге болады:
а) тригонометриялық функцияға қатысты квадратқа дейін;
б) тригонометриялық функцияға қатысты бөлшек-рационалды;
в) біртекті;
г) түрге дейін

Әдістемелік әдебиеттерде "дағдылар"ұғымының әртүрлі түсіндірмелері бар. Мысалы, Петровский а.в. "дағдылар" дегеніміз-қол жетімді деректерді, білімді немесе ұғымдарды пайдалану, заттардың маңызды қасиеттерін анықтау және белгілі бір теориялық немесе практикалық мәселелерді сәтті шешу үшін пайдалану мүмкіндігі.
Булыгинаның айтуынша, Т. Б. "дағдылар-бұл белгілі бір әрекетті саналы түрде орындау мүмкіндігі".
Матюхина М.в. келесі анықтама береді: "шеберлік - бұл қызметтің сәтті орындалуын қамтамасыз ететін білім мен дағдылардың үйлесімі". Дағдылар-бұл әрекеттерді орындаудың автоматтандырылған тәсілдері. Білім-бұл санадағы субъективті бейнелердің бір түрі. Тұжырымдама-бұл біртұтас және ерекше, бір уақытта әмбебап болып табылатын білім нысаны
Келесі тұжырымдаманы қарастырыңыз - "дағдыларды қалыптастыру". Бұл оқушының әлеуметтік тәжірибенің белгілі бір элементін игеруін ұйымдастырумен байланысты мұғалімнің қызметін білдіреді.
Дағдыларды қалыптастыру дегеніміз-білімдегі және тақырыптан алынған ақпаратты анықтау және өңдеу, ақпаратты іс-әрекеттермен салыстыру және байланыстыру бойынша операциялардың барлық күрделі жүйесін игеру.
Дағдыларды қалыптастыру, ең алдымен, барлық тереңдетілген білімнің өнімі ретінде әрекет етеді. Дағдылар зерттелетін объектілердің әртүрлі жақтары мен қасиеттері туралы түсініктерді игеру негізінде қалыптасады. Дағдыларды қалыптастырудың негізгі жолы-студенттерді объектідегі әртүрлі аспектілерді көруге, оған әртүрлі ұғымдарды қолдануға, осы объектінің әртүрлі қатынастарын тұжырымдамаларда қалыптастыруға үйрету. Оқушыларға талдау арқылы синтез көмегімен объектіні түрлендіруге үйрету керек. Қолданылатын түрлендірулер қандай қатынастар мен тәуелділіктерді орнату қажет екеніне байланысты. Мұндай өзгерістердің схемасы-мәселені шешудің жоспары.
Дағдыларды оқыту әртүрлі жолдармен жүзеге асырылуы мүмкін. Олардың бірі-оқушыға қажетті білім беріледі, содан кейін оларды қолдану міндеттері қойылады. Оқушының өзі шешімдер іздейді, сынақтар мен қателіктер арқылы тиісті нұсқаулықтарды, ақпаратты өңдеу әдістері мен қызмет әдістерін анықтайды. Бұл жол проблемалық оқыту деп аталады. Тағы бір тәсілі-студенттерге тапсырмалардың түрін және оны шешу үшін қажет операцияларды нақты тануға болатын белгілер үйретіледі. Бұл жол алгоритмдік оқыту немесе толық индикативті негізде оқыту деп аталады. Сонымен, үшінші жол-оқушыға білімді қолдану үшін қажет психикалық белсенділікті үйрету. Бұл жағдайда мұғалім оқушыны белгілер мен операцияларды таңдау нұсқауларымен таныстырып қана қоймайды, сонымен қатар оқушының тапсырмаларды шешу үшін алынған ақпаратты өңдеу және пайдалану жөніндегі қызметін ұйымдастырады. Бұған оқушыны зерттелетін тұжырымдамада бекітілген белгілерге назар аударуды талап ететін қызметтің барлық кезеңдері арқылы жүйелі түрде жүргізу арқылы қол жеткізіледі. Бірінші кезеңде пәннің бұл бағдарлары (маңызды белгілері) оқушыға дайын, материалдандырылған түрде, схемалар, символ, заттар түрінде ұсынылады, ал бағдарларды бөлу бойынша операциялар пәндік іс-әрекеттер түрінде жүзеге асырылады. Екінші кезеңде бағдарлар мен тақырыптық операциялар сөйлеу белгілері мен әрекеттерімен ауыстырылады. Үшінші кезеңде белсенділігі есептеледі және ауызша іс-әрекеттер, оларды ауыстырады ойлау операциялар және олар бойынша жүреді барлық свернутой схемасы. Бұл тұжырымдама ақыл-ой әрекеттерін кезең-кезеңмен қалыптастыру әдістемесі деп аталады.
Шын мәнінде, бұл кезеңдерді әр адам жаңа ұғымдарды қалыптастыруда өтеді. Алайда, әдеттегі жаттығулармен бұл кезеңдер саналы түрде ұйымдастырылмайды. Сондықтан студент қажетті маңызды немесе логикалық белгілерді іздеуге және табуға мәжбүр болады, ең бастысы - бұл әрекетті өзі таңдау. Қателер сөзсіз пайда болады. Ұғымдар әрдайым толық және шынайы бола бермейді. Нәтижелер арқылы "өзін-өзі" түсінуге және түзетуге негізделген дәстүрлі оқыту оқушының индикативті іс-әрекетінің толық еместігінің салдары болып табылады.
Сонымен қатар, оқушының іс - әрекеті ұғымдарды құруға, олардың белгілерін табуға емес, берілген ұғымдарды мағынамен толтыруға, яғни оларды қолдану тәсілдерін игеруге әкелмеуі керек-бұл тұжырымдамаларда бекітілген заттардың маңызды белгілерін тәуелсіз іздеу емес, осы белгілерді қолдану. Тұжырымдамалардың толық және дәл қалыптасуы үшін оқушының тиісті әрекеті толық индикативті негізде құрылуы керек. Басқаша айтқанда, мұғалім оқушыға объектілердің барлық маңызды белгілерін беруге және баланы оны анықтау және көбейту үшін белгілердің әрқайсысы талап ететін операцияларға үйретуі керек.
Тригонометриялық теңдеулер мен теңсіздіктерді шешу дағдылары туралы айта отырып, бұл дағдылар тұтас кешенді құрайтынын есте ұстаған жөн, оған мыналар кіреді:
- сандық шеңберде берілген сандарға сәйкес келетін, санның (және т. б.) және санның (М(2), М(-7), м(6) және т. б.) бөліктерінде көрсетілмеген нүктелерді табу мүмкіндігі;
- сандарды сандық шеңбердің нүктесімен бейнелеу және нүктелерді жазу мүмкіндігі (берілген нүктеге сәйкес келетін барлық сандарды анықтауды білдіреді);
- тригонометриялық функциялардың бірінің мәні бойынша сандық шеңбердегі сандарды бейнелеу мүмкіндігі;
- сандық шеңбер доғалары үшін қос теңсіздіктер құру;[20]
- теңдеуді белгілі түрлердің біріне жатқызу үшін негіз алу мақсатында ұсынылған теңдеуді немесе теңсіздікті талдау мүмкіндігі;
- шешім қабылдаудың негізделген таңдауын жүзеге асыру білігі;
- қарапайым Тригонометриялық теңдеулер мен теңсіздіктерді шеше білу және график, тригонометриялық шеңбер көмегімен шешімді суреттей білу;
- теңдеулер мен теңсіздіктерді шешуде тригонометриялық функциялардың қасиеттерін қолдана білу;
- ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.