Қарапайым гармоникалық осциллятор

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

«Ғ. ДАУКЕЕВ АТЫНДАҒЫ АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»

Коммерциялық емес акционерлік қоғамы

Техникалық физика кафедрасы

ФИЗИКА

Пәні бойынша

СӨЖ

Мамандығы: Автоматтандыру және басқару

Орындаған: Туркбенбаев Т. Ж.

Тобы: АУк-20-3

Тақырыбы: Гармоникалық осцилляторлар: физикалық және математикалық маятниктер.

Қабылдаған: аға оқытуышы Сыздыкова Р. Н.

Алматы 2021

Гармониялық осциллятор. Дененің күш әсерімен тербелу үрдісін сандық жағынан сипаттау үшін Ньютон механикасы заңдарын пайдалану қажет. Серіппенің серпімділік күші әсерінен тербелуші дененің (мысалы, шар) қозғалысын қарастырайық ( F = - kx ) . Үйкеліс күшінің қозғалысқа тигізетін әсерін есепке алмаймыз.

Жалпы классикалық механика, гармоникалық осциллятор ол оны тепе-теңдік жағдайынан шығарған кезде x ығысуына пропорционал F қайтару күшінің әсерін сезінетін жүйе::

$\overrightarrow{F} = - k\overrightarrow{x}$ ;

мұндағы k серпімділік коэффициенті.

Егер F жүйеге әсер ететін жалғыз күш болса, онда жүйе қарапайым немесе консервативті гармоникалық осциллятор деп аталады. Мұндай жүйенің еркін тербелістері тепе-теңдік жағдайына жақын мерзімді қозғалыс болып табылады. Жиілік пен амплитуда тұрақты, ал жиілік амплитудаға тәуелді емес.

Егер үйкеліс күші қозғалыс жылдамдығына пропорционалды болса, онда мұндай жүйе өшетін немесе диссипативті осциллятор деп аталады. Егер үйкеліс тым үлкен болмаса, онда жүйе периодты қозғалыс жасайды - тұрақты жиіліктегі және экспоненциалды түрде төмендейтін амплитудасы бар синусоидалы тербелістер. Өшетін осциллятордың еркін тербелістерінің жиілігі ұқсас үйкеліссіз осцилляторға қарағанда біршама төмен болады.

Егер осциллятор өздігінен қамтамасыз етілсе, ол еркін тербелістер жасайды. Егер сыртқы күш болса, осциллятор мәжбүр тербелістерді жасайды.

Гармоникалық осциллятордың механикалық мысалдары - математикалық маятник, серіппелі жүктеме, бұралу маятнигі және динамиктер. Гармоникалық осциллятордың механикалық емес аналогтарының арасында электрлік гармоникалық осцилляторды ажыратуға болады.

Егер уақытқа тәуелді сыртқы күш болса, гармоникалық осциллятор а ретінде сипатталады басқарылатын осциллятор .

Механикалық мысалдарға мыналар жатады: маятниктер және акустикалық жүйелер. Гармоникалық осциллятор моделі физикада өте маңызды, өйткені тұрақты тепе-теңдіктегі күшке кез-келген масса аз тербелістер үшін гармоникалық осциллятор рөлін атқарады. Гармоникалық осцилляторлар табиғатта кең таралған және көптеген қолдан жасалған құрылғыларда қолданылады, мысалы сағаттар және радио тізбектері. Олар іс жүзінде барлық синусоидалы тербелістер мен толқындардың көзі болып табылады.

Қарапайым гармоникалық осциллятор. Ол массадан тұрады м , бұл бір күшке ие F , ол массаны нүкте бағытына қарай тартады х = 0 және тек позицияға байланысты х масса және тұрақты к . Күштер балансы (Ньютонның екінші заңы) жүйе үшін

$F = ma = m\frac{d^{2}x}{dt^{2}} = m\ddot{x} = - kx$ .

Мұны шешу дифференциалдық теңдеу, біз қозғалыс функциямен сипатталатынын анықтаймыз:

$x(t) = A\cos(\omega t + \varphi)$

мұндағы

$\omega = \sqrt{\frac{k}{m}}$

Қозғалыс мерзімді, өзін а синусоидалы тұрақты амплитудасы бар сән A . Амплитудасынан басқа қарапайым гармоникалық осциллятордың қозғалысы оның сипаттамасымен сипатталады кезең $T = \frac{2\pi}{\omega}$ , бір тербеліс уақыты немесе оның жиілігі $f = \frac{1}{T}$ , уақыт бірлігіндегі цикл саны. Берілген уақыттағы позиция т байланысты фаза φ , бұл синус толқынындағы бастапқы нүктені анықтайды. Период пен жиілік массаның өлшемімен анықталады м және күш тұрақтысы к , ал амплитудасы мен фазасы бастапқы күйімен анықталады және жылдамдық.

Жылдамдық және үдеу қарапайым гармоникалық осциллятордың орналасуы бірдей, бірақ фазалары ауысқан тербеліс. Жылдамдық нөлдік орын ауыстыру үшін максималды, ал үдеу ығысуға қарама-қарсы бағытта болады.

Қарапайым гармоникалық осцилляторда орналасқан потенциалдық энергия х болып табылады:

$U = \frac{1}{2}kx^{2}$

Жаппай серіппелі гармоникалық осциллятор

Қарапайым гармоникалық қозғалыс

Сөндірілген гармоникалық осциллятор. Нақты осцилляторларда үйкеліс немесе демпфинг жүйенің қозғалысын баяулатады. Үйкеліс күшінің әсерінен жылдамдық әрекет етуші үйкеліс күшіне пропорционалды түрде азаяды. Қарапайым итерілмеген гармоникалық осцилляторда массаға әсер ететін жалғыз күш - қалпына келтіру күші болса, демприрленген гармоникалық осцилляторда оған қосымша әрдайым қозғалысқа қарсы бағытта болатын үйкеліс күші болады. Көптеген діріл жүйелерінде үйкеліс күші F _f жылдамдыққа пропорционалды ретінде модельдеуге болады v объектінің: F _f = − резюме , мұнда c деп аталады тұтқыр демпфер коэффициенті .

Күштер тепе-теңдігі (Ньютонның екінші заңы) демпирленген гармоникалық осцилляторлар үшін:

$F = - kx - c_{\overline{\mathbb{d}t}}^{\mathbb{d}x} = m\frac{\mathbb{d}^{2}x}{\mathbb{d}t^{2}}$

оны формаға қайта жазуға болады.

Маятник дегеніміз - өзіне түсірілген күштердің әсерінен қозғалмайтын нүктенің немесе осьтің төңірегінде тербелетін қатты дене. Әдетте маятник деп ауырлық күші әсерінен тербеліс жасайтын денені атайды. Осы кезде маятниктің осі оның ауырлық центрі арқылы өтпеуі тиіс.

Математикалық маятник деп созылмайтын салмақсыз жіңішке ұзын жіпке ілінген кішкентай ауыр шарды айтады.

Тербелмелі жүйелерге тән белгілердің бәрі математикалық маятникте де болады. Егер маятникті тепе-теңдік күйінен ауытқытсақ, онда ол әрекет етуші күштерді теңгеруші күштің әрекетінен бастапқы тепе-теңдік күйіне қайта оралады. Осындай маятниктердің қозғалысын бақылай отырып, келесі қарапайым заңдарды тағайындауға болады.

Егер маятниктің ұзындығын өзгертпей, оған массалары әр түрлі жүктер ілсек, онда маятниктің тербеліс периодының өзгермейтіні байқалады. Демек, математикалық маятниктің периоды жүктің массасына тәуелді болмайды.
Егер маятникті қозғалысқа келтіргенде оны әр түрлі бұрышқа (бірақ өте үлкен емес) ауытқытатын болсақ, онда ол амплитудасы түрліше болғанымен, бірдей периодпен тербеледі. Амплитудасы өте үлкен болмаған жағдайда бұл тербеліс гармоникалық тербеліске мейлінше жуық болады. Математикалық маятниктің периоды тербеліс амплитудасына тәуелді болмайды.
Маятниктің ұзындығын өзгерте отырып, тәжірибені қайталасақ, тербеліс периодының маятник ұзындығына тәуелді болатынына көз жеткіземіз. Демек, маятник неғұрлым ұзын болса, тербеліс периоды соғұрлым көп болады. Ал, керісінше, маятник неғұрлым қысқа болса, тербеліс периоды соғұрлым аз болады.

Математикалық маятник тербелісінің формуласын қорытып шығарайық. Маятник тербеліп тұрғанда жүк АВ доғасының бойымен Fқ кері қайтарушы, яғни қорытқы күштің әрекетінен үдеумен қозғалады. Бұл күштің шамасы қозғалыс кезінде өзгеріп отырады. Ал дененің мұндай тұрақсыз күштің әрекетінен қозғалысын есептеу өте күрделі. Сондықтан есептеуді жеңілдету үшін біз былай жасаймыз: маятникті бір жазықтықта тербелтпей, жүк шеңбер бойымен қозғалатындай етіп, оны конус сызуға мәжбүр етеміз.

Маятниктің айналу периоды оның тербеліс периодына тең болады: Т _айн = Т _тер = Т .

Конустық маятниктің айналу периоды жүк сызатын шеңбердің ұзындығын сызықтық жылдамдыққа бөлгенге тең:

T=2πR/ν

Ал маятник вертикаль күйінен шамалы ғана ауытқитын болса, амплитуда аз болғанда, қорытқы күш шеңбердің ВС радиусы бойымен бағытталады деп есептеуге болады. Бұл жағдайда қорытқы күш центрге тартқыш күшке тең:

F=mν ² /R

Екінші жағынан, ОВС және BDE үшбұрыштарының ұқсастығынан: BE : BD = CB : ОС немесе F: mg = R : l, бұдан

F=mgR/l

F күшінің осы екі өрнегін теңестіре отырып aлатынымыз:

mν ² /R=mgR/l

ν ² =gR2/l

ν=R $\sqrt{\frac{g}{l}}$

Осыны T периодтың өрнегіне қойып, мынаны табамыз:

T=2πR/R $\sqrt{\frac{g}{l}}$ =2π $\sqrt{\frac{g}{l}}$

T=2π $\sqrt{\frac{g}{l}}$

Сөйтіп, математикалық маятниктің тербеліс периоды g еркін түсу үдеуі мен маятниктің I ұзындығына ғана тәуелді болады. Алынған формула маятниктің тербеліс периоды оның массасы мен тербеліс амплитудасына (ол өте аз болғанда) емес, тек маятниктің I ұзындығы мен g еркін түсу үдеуіне ғана тәуелді болатынын көрсетеді.

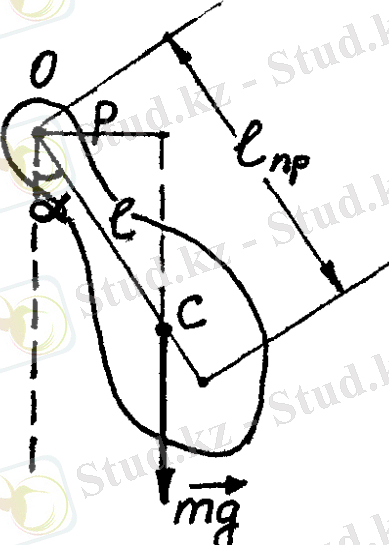
Физикалық маятник деп ауырлық күшінің әсерінен дененің ауырлық центрі арқылы өтпейтін оське қатысты тербеліс жасайтын қатты денені айтады.